基于GA-BP神经网络的列车关键部件预防性维修优化模型及应用

周志恒，贺德强,2，陈彦君,2，张小振，沈国强

(1.广西大学 机械工程学院，广西 南宁530004；2.广西制造系统与先进制造技术重点实验室，广西 南宁530004；3.南宁轨道交通集团有限责任公司，广西 南宁530029)

我国现行的地铁维护措施主要以故障修和定期维修措施为主[1]，但是这种模式往往伴随着过维修和欠维修情况的存在。国内外学者针对以上缺陷对地铁列车的维修模式开展了相应的优化研究。马亮等[2]以地铁检修制度和班组检修能力为基础，建立以检修次数最多和平均利用率最高为目标的列车多目标预防性维修模型，整体提升了行车基地的检修效率和列车利用率；王灵芝等[3−4]通过建立三参威布尔维修模型，利用相关系数法和最小二乘法，提高参数估计精度，简化计算过程；同时以生产设备为研究对象，在可靠性下降的情况下提出了成组维修的费用优化模型，在保证设备安全运行前提下找到了最优维修策略；贺德强等[5]提出一种考虑机会维修阈值的预防性维修优化模型，综合分析机会役龄因子和安全失效概率因子对维修策略的影响，最终达到减少维修次数、降低维修费用、提高列车正线运营率的目的；AN‐TONIO等[6]引入ETT(Economic Type Turning)维 修选项，通过建立寿命周期成本模型来估算列车轮对的磨损演化情况，结果表明，ETT在复杂轮对维修策略下可节约成本2.0%～4.7%；HOSSEINI等[7]结合成本优化法和模糊层次分析法，提出一种系统要素维护成本优化模型，将维修费用确定为系统可靠性指标和预防性维修预算的函数，为维修预算提供了新的指导；EISENBERGER等[8]结合蒙特卡罗仿真，将Petri网运用到铁路机车的维修中，提出一种适用于列车维修评估的APN方法，并结合理论案例验证了此方法的实用性；RICH‐ARD等[9]提出一种包含多种维修方式的选择维修策略，利用威布尔分布对部件寿命进行建模，以维修费用和维修时长为约束条件求解目标函数，为系统维修方案提供理论参考。对故障率进行预测同样是一种维修策略优化方法，通过对未来故障率进行预测，为现行维修策略提供参考。刘奇等[10]研究车载ATP设备的故障率趋势，利用思维进化算法优化Elman神经网络，构建Chaos-Elman预测模型，经仿真试验验证最终预测精度为95%；宋云等[11]通过建立双通道传感器故障检测模型，在径向基神经网络的基础上提出3种维修策略，可准确发现故障信号；郭宇等[12]利用灰色关联分析和粗糙集理论对故障数据进行横向和纵向约简，利用处理后的数据作为BP神经网络的输入，根据输出结果预测设备的故障状况。综合以上分析，目前的预防性维修策略多是基于安全性、经济性或高效性的单一优化目标，缺乏考虑多目标优化维修策略。对于故障的预测也多是基于理论，没有结合实际维修模型，预测结果仅作为维修指标的一项参考，不能发挥神经网络强大的映射能力。针对上述问题，本文综合考虑安全性、经济性和高效性因素，将遗传算法改进的BP神经网络和预防性维修模型相结合，建立以维修费用为目标函数，列车运行可靠度和预防性维修次数为决策变量的不完全维修模型。首先建立GA-BP神经网络预测模型，统计整理地铁列车历史故障数据，将该数据作为神经网络的输入对可靠度进行预测；然后分析列车实际运行情况，将可靠度预测结果和预防性维修次数作为决策变量，以单位时间维修费用最小为目标，建立变周期的不完全预防性维修模型，从而达到维修费用最小且列车使用率最高的目的。

1 GA-BP神经网络预测模型

可靠度是列车安全运行的一项重要指标，对于可靠度的预测越精确，越能为维修提供实际依据。地铁列车是集成机械、电子、网络等系统的复杂结构设备，通常情况下地铁列车发生故障的情况呈高度非线性映射关系，而神经网络在非线性关系的映射上具有突出优势。可靠度预测的关键在于预测模型的精度是否达到要求。

1.1 GA-BP神经网络搭建

BP神经网络是一种非线性系统的网络拓扑结构，核心处理单元为大量的人工神经元，是一种多输入、单输出的非线性处理单元[15]。它的输入表达式和输出表达式如下：

式中：ωij为i到j的连接权值；xi为输入信号；θj为人工神经元阈值；n为输入信号的数量；yi是神经元输出；f(hi)是激活函数。

BP神经网络一般由3层或者3层以上结构组成，本文选取3层模型[12]，包括输入层、隐藏层和输出层，各层之间的连接权值类似于神经元细胞间的纤维强度。当经过归一化处理的数据经由输入层输入神经网络之后，经过隐藏层向输出层传播，在输出层获得经由神经网络处理之后的预测输出，预测输出与期望输出对比得出神经网络的预测精度。

本文采用遗传算法改进的BP神经网络。遗传算法能够选择进化好的个体作为最优解，克服了传统BP神经网络易陷入局部最优的缺陷。

遗传算法的核心主要包括选择、交叉和变异操作。遗传算法改进BP神经网络的目的是为了获取最优连接权重和阈值。首先确定神经网络拓扑结构，生成初始权重和阈值，遗传算法对初始权重和阈值进行编码，确定适应度函数之后进行选择、交叉和变异操作，将满足条件的最优权重和阈值代入网络进行训练，具体工作流程如图1所示。

图1 GA-BP神经网络工作流程Fig.1 GA-BP neural network workflow

1.2 数据采集与处理

用于模型计算的故障数据均来自某市轨道交通车辆中心故障统计表，统计范围包含该市一号线车门系统故障时间间隔，根据故障时间间隔推算出故障天数。车门任意部件发生故障即视为车门故障，根据故障发生时间记录车门系统各部件的故障时间间隔，其中同一天内多车同种部件发生故障的情况视为一个部件故障，统计时视为1。针对不同部位同周期内故障次数不同导致的数据不对等情况，在整理数据时根据故障发生时间加以取舍，根据故障统计表删除记录不足的数据，并且忽略异常数据。本文统计范围包含双周检、3月检和年检，并且记录列车的正线故障情况。故障天数统计情况如表1所示。

对于可靠度估算，常用到中位秩法[14]。在样本容量较小的情况下，中位秩法估算可靠度可有效减小误差，中位秩法估算可靠度的计算公式如下：

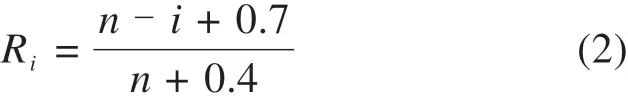
式中：Ri表示第i次故障时的可靠度；n为统计的样本总容量；i表示部件故障次数。

将表1中的数据依次代入式(2)中，可以得到车门系统各部件每次发生故障时的可靠度，为了保证列车安全运行，将可靠度置信范围设定为50%，低于50%的数据不作为神经网络的训练集和测试集，统计获得包含下挡销、平衡压轮等部件的6组各30个数据，可靠度统计如表2所示。

表1 车门系统各部件故障时间Table 1 Failure time of door system components

根据统计数据，本文把车门系统各部件的可靠度作为神经网络的输入和输出，将表2中的6组数据的前5组作为神经网络的输入数据，第6组作为期望输出，6组数据中的前20个数据作为神经网络的训练集，后10个数据作为测试集。

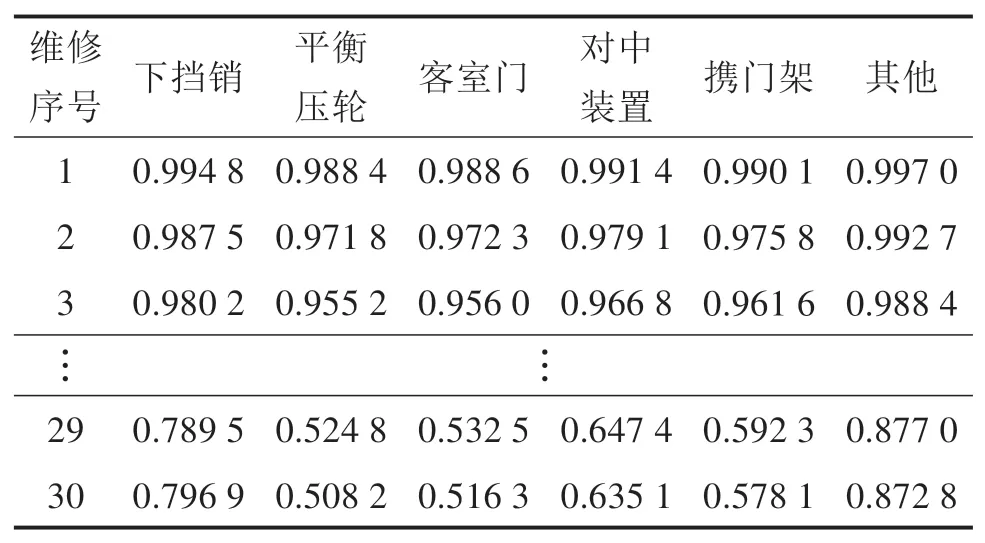
表2 车门系统各部件可靠度Table 2 Reliability of door system components

由此可以确定神经网络输入神经元节点数为5，输出神经元节点数为1，隐藏层神经元节点数由经验公式推算可得，公式如下：

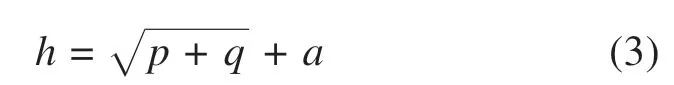
式中：p表示输入神经元节点数；q表示输出神经元节点数；a表示(1,10)之间的整数。经过调试，确定h为5时误差最小。

最终，GA-BP神经网络确定为5-5-1 3层神经网络结构。

1.3 仿真过程

仿真参数设置如下：遗传算法迭代次数设置为50，种群规模为20，交叉和变异概率设置为0.1，神经网络最大迭代次数设置为20，学习效率为0.1，目标设置为0.000 1。最终获得仿真结果如图2所示。

图2 反映的是GA-BP神经网络预测模型和传统BP神经网络预测模型的预测故障率和历史故障率的对比结果，可以看出，经过遗传算法改进的BP神经网络预测模型图像的拟合度更高，预测准确度比传统神经网络预测结果高20%，由此认为GA-BP神经网络预测结果基本可以反应未来实际的可靠度。图3显示了遗传算法的寻优过程，其适应度在第24代时收敛到0.001 2，预测值符合期望值的趋势。

图2 神经网络预测结果对比Fig.2 GA-BP neural network output results

图3 适应度函数曲线Fig.3 Fitness function curve

综上所述，神经网络对于可靠度的预测具有一定的可行性，基于历史数据预测所得结果可以作为列车关键部件预防性维修优化模型的约束条件，达到列车关键部件预防性维修费用最低的要求。

2 列车关键部件预防性维修优化模型

预防性维修模型的建立围绕可靠度、维修次数及维修费用展开，结合第2节所得预测结果，实现列车关键部件预防性维修优化模型目标函数最优取值。

假设预防性维修在一个固定的检修周期内进行，部件维修模式由最小修、故障修、预防性维修和更换维修构成。最小修即日常维护，检测出缺陷并排除，不影响列车正常运行时间；故障修指发生故障之后的维修，即事后维修。此模式下列车的正常运行受到不同程度的影响，影响程度视故障类型而定。为简化建模，本文对此维修模式视为统一故障类型，列成停运时间相同，单位时间的损失相同；更换维修即部件可靠性达到更换阈值，采取更换部件的维修模式。

2.1 预防性维修模型建立

部件初始役龄均为0，假设维修在更换周期[0,T]区间内进行分析，在此区间内共进行M次预防性维修，维修次数达到M时进行更换维修。更换周期T由M个预防性维修周期组成，如式(4)所示。

维修策略既定预防性维修是停机维修，预防性维修安排在非运营时间段进行，[0,T]区间不包含预防性维修时间；故障修一般发生在列车正常运行时间段内，故[0,T]区间内包含故障修时间；更换多为架修，此阶段耗费时间较长，非运营时间不足以囊括更换维修，所以[0,T]区间也包含更换维修时间；最小修为日检，此时间较短且费用较小，故在本文中忽略不计。

设Ti为第i个预防性维修周期，tg为平均故障修时间，Ni为第i次预防性维修周期内故障次数，则第i个预防性维修周期内正常工作的时间Twi为：

在部件运行一段时间后，部件的役龄和故障率都有所增加，本文引入役龄回退因子α，在对部件进行维修时，故障率会下降到预防性维修前αTi时刻，相当于部件役龄回退，回退量为αTi，此时部件实际役龄Ts的表达式为：

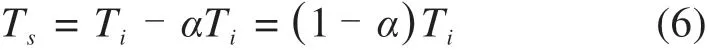
部件在运行期间属于损耗阶段，其故障率呈递增趋势，且故障率分布符合威布尔分布，根据威布尔分布模型，设λ(t)为部件的故障率函数，R(t)为部件可靠性函数，由威布尔分布模型可得：

式中：β为部件的形状参数；η为部件特征寿命参数，两者均可通过分析部件的历史故障数据得到。

经过预防性维修，部件的故障率变化规律呈递推模式，变化规律表达式如式（9）所示。

由式(9)可得部件在进行第i次预防性维修后故障率函数为：

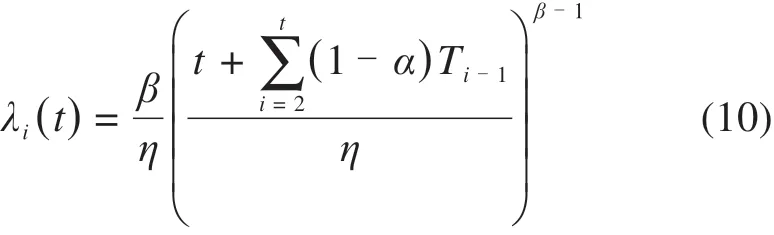
进而得到基于威布尔分布模型的部件预防性维修可靠性函数为：

故障小修的次数可以由预防性维修周期内的累计故障率表示，如式(12)所示。

为了提高列车的任务性，在做预防性维修的同时也要考虑列车的可用度。可用度是衡量部件性能好坏的重要指标，表示长期运行状态下部件正常工作时间所占比例，用A来表示，即：

其中MUT表示平均正常运行时间，MDT表示平均不运行时间。由式(4)～(5)可得：

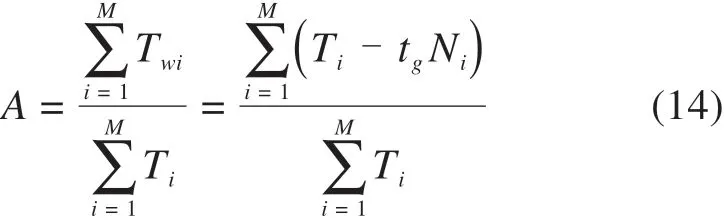
2.2 维护费用模型

本文设定的目标函数为维修费用函数，其中维修费用又包含在维修周期内的损失费用。设维修周期[0,T]内的总维修费用为Cm：

式中：Cp为预防性维修总费用；Cl为故障小修总费用；Cr为更换维修总费用；Cs为故障停车损失总费用。维修策略中最小修一般为日常检查，此部分费用较小，不作为本文考虑因素。

假设单次故障修费用为Ca l，由式(12)可得故障修总费用Cl：

更换维修在周期内预防性维修次数达到M时进行，不排除在周期内发生重大变故导致部件更换的可能性，这种可能性在本文不加以考虑，所以更换维修总费用Cr为定值。

其中，τl为故障修单位停车时间，τr为更换维修停车时间。

综上，由式(16)，(17)和(18)可得：

最后得到基于威布尔分布的预防性维修优化模型目标函数：

3 列车车门系统算例分析

3.1 模型参数估计

本文采用图参数估计法求解威布尔模型中的参数。将威布尔模型线性化，对可靠度进行2次自然对数变换将其线性化，得：

令y=ln{-ln[R(t)]}，x=ln(t)，a=β，b=-βln(η)，则2次自然对数变换后的线性公式为：

其中，x由统计的车门系统维修时间求得，y由每次维修时间对应的可靠度求得。本文选择故障次数较多的下挡销、平衡压轮和客室门3个部件作为威布尔模型参数的拟合对象，各部件拟合方程参数结果如表3所示。

表3 拟合方程参数Tab.3 Parameter of fitting equation

对于役龄回退因子α的选取，本文设定役龄回退因子α=0.95。

3.2 基于量子遗传算法的模型求解

本文采用量子遗传算法来进行改进。量子遗传算法是量子计算和遗传算法相结合的产物，该算法具有并行计算的能力，其优势在于通用性高，搜索效率高等。

将威布尔模型参数代入目标函数，利用目标函数及其约束条件，基于第2节神经网络所得可靠度，设置神经网络得出的可靠度R(t)及一个周期内最佳维修次数M作为决策变量，可以求得满足列车高效性、经济性的预防性维修时间间隔TM。

量子遗传算法将量子计算和量子旋转门等概念引入传统遗传算法，通过量子位表达基因、量子交叉和量子变异等操作来提高算法的效率。量子遗传算法仿真流程如图4所示。

图4 量子遗传算法仿真流程Fig.4 Quantum genetic algorithm simulation flow

3.3 实例验证

本文选择车门系统故障次数较多的下挡销、平衡压轮和客室门3个部件作为模型的验证案例，考察3个部件一个更换周期(1年)内的维修情况。维修模型总体参数设置如表4所示。

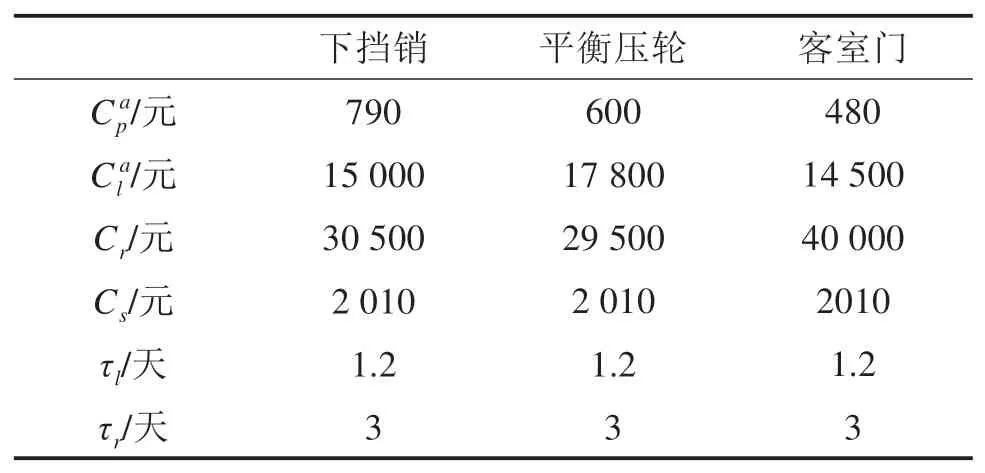
表4 模型参数设置Table 4 Model parameter setting table

通过MATLAB仿真，在获得全部参数的情况下，采用上文所提到的量子遗传算法对维修次数和单位时间维修费用2个维修策略目标函数进行寻优求解。

设置量子遗传算法迭代次数MAXGEN=50，种群大小sizepop=50，每个变量的二进制编码长度为20。利用MATLAB编程仿真计算，获得2个维修决策变量的最佳适应度迭代图，如图5所示。

从图5可知，现行维修模式的适应度在第24次迭代时开始收敛，而本文模型中下挡销、平衡压轮和客室门的适应度均在第8次迭代时收敛到全局最优，收敛速度比现行维修模式快66.6%。最优值输出分别为23.50元、26.00元和25.44元，即日均维修费用最小为24.98元。部件可靠度最优输出分别为0.978，0.968和0.977，周期内最佳预防性维修次数均为6次。

图5 量子遗传算法迭代曲线Fig.5 Quantum genetic algorithm iterative curve

为了验证本文模型的可行性以及相较于现行维修模式的优越性，将其与现行维修模式进行比较，如表5所示。

由表5可知，在一个更换周期(1 a)内，现行检修模式实行定周期月检，年维修次数12次，本文模型计算所得3种部件最佳维修次数均为6次，相较于现行检修模式维修次数减少50%；3种部件日均维修费用24.98元，日均维修费用相较于现行维修模式节省约24.07%。同时列车运行可靠性相较于现行检修模式提高约3.4%。因此，采用本文模型可以在保证列车安全高效的前提下降低日均维修费用。

表5 维修模式对比结果Table 5 Maintenance mode comparison results

4 结论

1)综合考虑列车运行的安全性、经济型和高效性，建立基于可靠度的预防性维修模型，与现行检修模式的定周期制度相比，变周期维修模式更能满足列车安全、高效的运行要求。

2)不完全预防性维修模型决策变量基于GABP神经网络，预测数据基于历史故障数据，符合故障相关属性，避免直接以历史故障数据计算可靠度带来的不确定性。

3)基于GA-BP神经网络的地铁列车不完全预防性维修模型可以使列车保持在高可靠度的状态下运行，提高了列车安全性；同时周期内维修次数降低，提高列车可靠度，列车日均维修费用节省约24.07%，列车可靠度提高约3.4%。

4)本文模型基于历史故障数据，是现行检修模式的改进，具有可行性，可以为地铁列车维修模式优化提供参考。