增强约束条件下地铁二线纵断面自动生成方法
梁柱,陈继,钟晶,孟存喜,李伟,蒲浩
(1.中南大学 土木工程学院,湖南 长沙410075;2.高速铁路建造技术国家工程实验室,湖南 长沙410075;3.中铁第一勘察设计院集团有限公司,陕西 西安710043;4.轨道交通工程信息化国家重点实验室,陕西 西安710043;5.中铁第四勘察设计院集团有限公司,湖北 武汉430063)
地铁二线纵断面的几何形位不仅要满足设计规范中的几何常规约束,还要与基线全线重要工点位置相适应,如二线设计时,基线车站,横向联络通道及排水泵房等选址定位均已完成,限制了二线纵断面的空间位置,构成增强约束。人工设计时设计人员必须耗费大量的精力逐个坡段进行手工调整,而且调整过程中会产生连锁效应,需要反复迭代才能产生满足所有约束的纵坡方案,严重制约设计效率,因此迫切需要借助计算机开展辅助设计,其主要难点为:1)全线坡段数量众多,相邻坡段的调整互相影响,会改变坡段长度及变坡点位置,当不能满足约束要求时需要重复返工;2)排水泵房与横向联络通道设置在相邻车站间最低点,要求基线与二线最低点高程一致且能垂直连接,而该位置处于竖曲线上,需要反复试算调整方能满足要求。因此,地铁二线纵断面设计需耗费大量时间与精力进行方案调整以满足规范等常规约束以及重要结构物联合设置等增强约束,迫切需要借助高效的计算机辅助技术对地铁二线纵断面进行高效的精细化调整,自动产生高质量的地铁二线纵断面方案供设计者参考及进一步优化,以提高设计效率。轨道线路纵断面设计一直是国内外研究的热点,现有研究主要是将优化算法[1−6](Fwa,2002;Goktepe,2009;Hare,2015;Ghanizaneh,2018;Booto,2019;Pu,2019)应用于纵断面优化过程,以节能环保,经济适用,安全舒适等作为优化目标,并不考虑与既有结构的匹配关系,约束条件与本文所研究问题存在较大差异。开展地铁二线纵断面自动设计时,要最大限度的产生适用范围广的设计方案,满足复杂的约束条件以减轻设计者的二次优化负担。因此,地铁二线纵断面自动设计不仅包含《地铁设计规范》[7]对纵断面坡度限值、坡段长度及竖曲线半径等常规约束,还包含车站,横向联络通道及泵房结构联合设置等多项增强约束。对此,许多学者为提高方案设计质量和效率,对地铁纵断面调整方法进行了研究:如李洪强[8]总结了坡段长与坡度值两者的叠加调整方法;任碧能[9]采用“上下限法”协同变坡点与竖曲线半径关系;叶霞飞等[10]对地铁纵断面调整的常规方法进行了概括;黄铂清[11]总结了以变坡点里程、高程为设计变量的纵断面调整模型,并对模型的约束条件进行了细致分析。以上针对纵断面几何线形的研究能很好解决坡度,坡段长度及竖曲线半径等常规约束下的线路调整问题,但对于纵断面沿线重要工程结构物的设置未作讨论。有关车站及排水泵房的研究包括郭俊义[12]指出了地铁车站所处坡段的设计要求;李睿等[13]阐述了地铁纵断面基线与二线共同设置排水泵房的配合标准;但是这类研究也仅仅局限于结构物所在坡段,不考虑相邻坡段相互影响问题,未将规范限定的常规约束和因地铁基线方案设计,重要工点选址所产生的增强约束进行组合。刘志雄[14]论述了区间V形变坡点最低点的轨面高程计算原理,为计算最低点位置提供了数学方法,但这种方法是基于确定的两侧坡段计算最低点的正向过程,并非本文所面临的基于最低点数据调整两侧坡段的反向过程。针对以上问题,本文提出负反馈线性转化求交法,将复杂的调整过程分治于“参照法初始化—常规约束调整—增强约束调整—负反馈检测与调整”4个阶段,主要过程如下:
1)参照地铁基线纵断面,快速构建二线初始纵断面,并按照竖曲线半径>坡度值>坡段长的优先级顺序,对纵断面几何线形进行有序检测与调整,生成满足规范约束的初步调整纵断面;
2)以车站为界,划分单位区间。对车站基线与二线站台范围轨面平行等高约束进行参数化表达;
3)利用相邻坡段与竖曲线几何关系V形坡变坡点里程及轨面高程,将精细化的人工调整过程进行数学化表达,充分满足合设横向联络通道及泵房约束,解决了于竖曲线最低点联合设置排水泵房及联络通道问题;
4)引入负反馈机制再次对各常规约束进行后处理,保证最终方案的有效性。
1 地铁二线纵断面约束
地铁二线纵断面设计综合了《地铁设计规范》[7]所限定的常规约束和重要工点定位(车站,横向联络通道及排水泵房)引入的增强约束。
1.1 纵断面常规约束
规范对地铁纵断面所作约束主要包括竖曲线半径R,坡度上、下限值imin和imax及最小坡段长为Lmin,应分别满足如下规定:
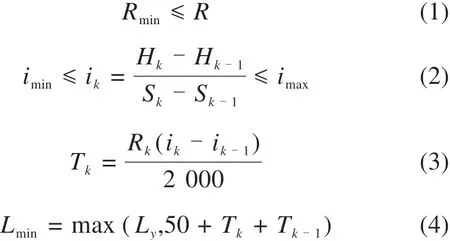
式中:Hk,ik,Rk,Tk和Sk分别为第k个变坡点轨面高程、坡度值、竖曲线半径、切线长及连续里程,变坡点号k取值范围∀k=1,2,…,n。Ly为远期列车长。
1.2 地铁二线纵断面增强约束
为保留基线与二线站台共用车站设备的条件,向设计人员提供更为有利的优化空间,要求站台范围轨面平行等高,以达到便利旅客乘降,节约用地,减少工程投资等目标[15]。并且,将横向联络通道与排水泵房合设于V形坡的最低点,并实现基线与二线联合设置需求,以达到区间汇水,横向排水和紧急情况下消防、疏散等目的[14]。
1.2.1 站台范围轨面平行等高约束
地铁基线与二线在平纵面在车站位置汇集,为保留共用车站设备的条件,在站台范围内,任意横断面上基线与二线轨面平行等高,即满足:
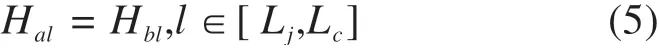
式中:Hal及Hbl分别表示车站基线与二线在l里程处轨面高程值,Lj与Lc为进出站站台连续里程。
1.2.2 横向联络通道与泵房合设
横向联络通道与泵房具有沟通基线与二线的功能[16],设置时要求横向联络通道中轴线与基线及二线在平面上相交,并垂直于基线,严格控制其所处位置在基线及二线纵断面上轨面高程一致。
根据基线纵断面方案,以相邻车站中心为界,划分线路单位区间,并按图1所示,以V形坡变坡点k连续里程Sk,设计高程Hk,竖曲线半径Rk及两侧坡度值ik-1与ik为已知条件,求解V形坡最低点Ak连续里程ALk,2j-1及设计高程AHk,2j。

图1 V形坡最低点计算示意图Fig.1 Schematic diagram of calculation of the lowest point of V-shaped slope
根据两侧坡段坡度绝对值大小关系,V形坡最低点连续里程ALk,2j-1及设计高程AHk,2j按照式(6)计算。
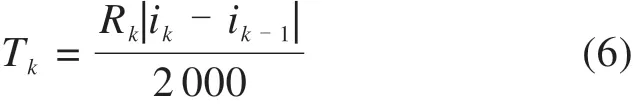

以各相邻车站中心为界,将全线划分为m个单位区间,利用式(6)~(8)计算各单位区间V形坡最低点连续里程及轨面高程,并整合形成控制

式中:下标m,n表示单位区间个数及单个区间V形坡最低点数量最大值。为满足合设横向联络通道及泵房需要,如图2所示,基线与二线纵断面V形坡最低点轨面高程相等。并且,基线平面与二线平面V形坡最低点位置连线(横线联络通道中轴线)垂直于基线平面,记为映射关系:

图2 基线与二线平纵断面V形坡最低点示意图Fig.2 Schematic diagram of the lowest point of V-shaped slope between the baseline and the second-line horizontal and vertical alignments
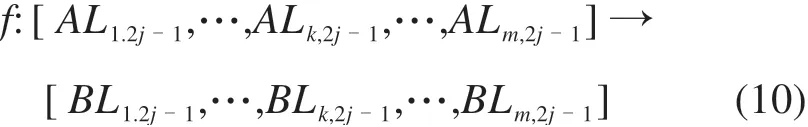
为保持基线与二线纵断面各V形坡最低点轨面高程一致,则要求基线纵断面任意区间任意V形坡最低点高程AH2j与二线对应区间及V形坡最低点BH2j相等:
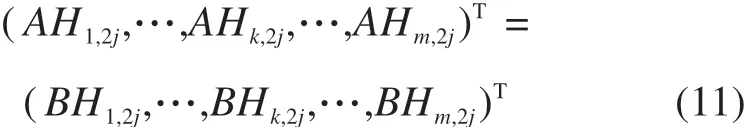
根据式(10)~(11)整理得到与Am×2n对应的二线约束控制矩阵Bm×2n。
Am×2n与Bm×2n为 同 型 矩 阵,其 相 关 性 可 根 据奇、偶列向量进行分别表述:
奇数列:二线V形坡最低点所属二线平面位置在基线平面的投影里程即基线V形坡最低点连续里程;
偶数列:基线与二线纵断面对应单位区间各V形坡最低点轨面高程相等。
2 地铁二线纵断面自动生成与增强约束调整模型
增强约束条件下地铁二线纵断面自动生成按照“参照法初始化—常规约束调整—增强约束调整—负反馈检测与调整”实现分步设计,最终自动生成能满足工程实际约束条件的纵断面方案,其实现流程如图3所示。
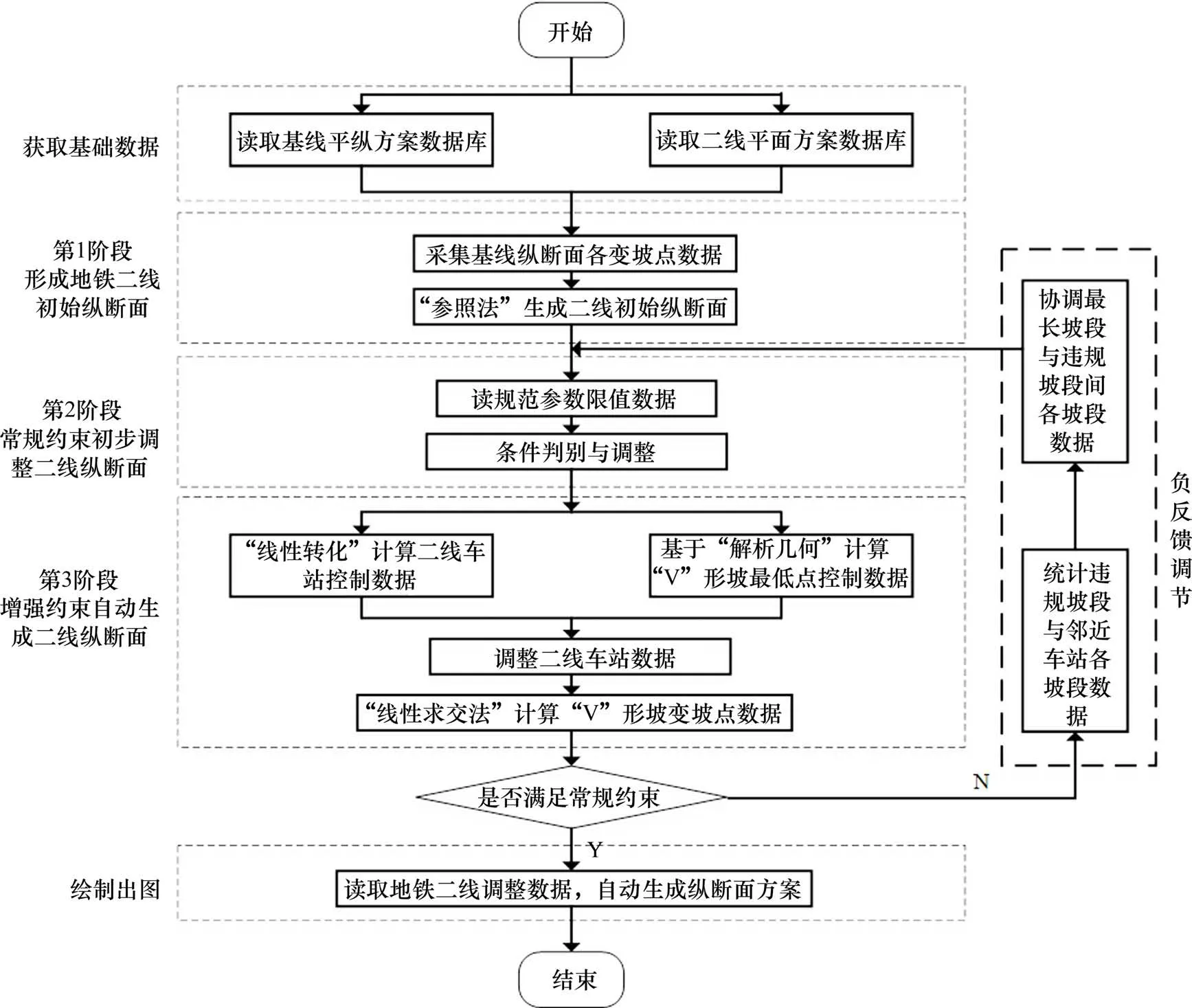
图3 增强约束条件下地铁二线纵断面自动生成方法Fig.3 Research idea of automatic generation method of second-line vertical section of metro under enhanced constraints
2.1 二线初始纵断面
首先参照基线纵断面数据,构建二线纵断面初始方案。如图4所示,根据基线纵断面变坡点k连续里程Sk锁定其在平面线位上的大地坐标(N,E),并沿基线平面法线方向求解其在二线的投影点(N′,E′),在二线平面方案中计算点(N′,E′)处的连续里程,并将其作为二线纵断面k2变坡点连续里程Sk2,保证(N′,E′)点与(N,E)点设计高程相等,并以基线各变坡点竖曲线半径初始化二线各变坡点竖曲线半径,形成地铁二线初始纵断面。
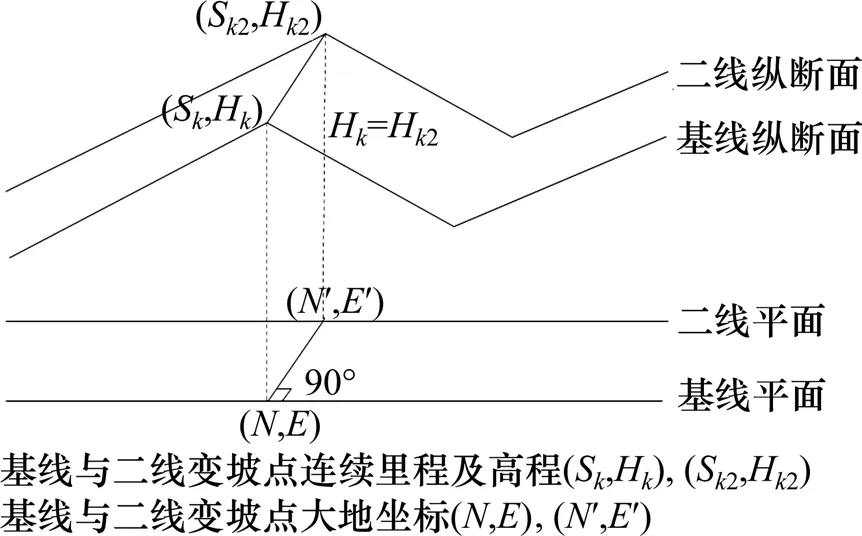
图4 参照基线初始化二线Fig.4 Refer to the baseline and initialize the second-line
2.2 常规约束调整
对二线初始纵断面各变坡点常规约束进行检测与调整。对原始二线数据逐步进行竖曲线半径,坡度值及坡段长的约束检测,并对违规内容进行更新调整,最终达成常规约束,执行流程如图5所示。

图5 二线初始纵断面常规约束调整流程图Fig.5 Flow chart of conventional constraints adjustment of second-line
2.3 增强约束调整
2.3.1 站台范围轨面平行等高
地铁车站站台范围内,将基线与二线的轨面进行平行等高处理可为共用站台设备提供有利条件。由于车站站台范围各断面轨面高程值线性连续变化,因此通过保证基线与二线车站站台中心里程处轨面高程及所在坡段坡度值一致,可将该约束线性化,如图6所示,即:
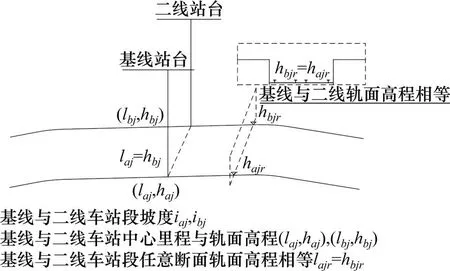
图6 车站坡段约束条件示意图Fig.6 Schematic diagram of constraints on the slope within the station

2.3.2 横向联络通道与泵房合设
为满足同型矩阵Am×2n及Bm×2n奇偶列向量各元素对应约束,要利用V形变坡点的最低点数据(BLk,2j-1,BHk,2j)确定V形坡变坡点连续里程及设计高程数据(Sk,Hk)。如图7所示,已知目标变坡点(Sk,Hk)两侧相邻变坡点(x2,y2),(x3,y3),V形坡变坡点的最低点(BLk,2j-1,BHk,2j)及竖曲线半径Rk,首先根据式(13)确定竖曲线圆心(x1,y1):
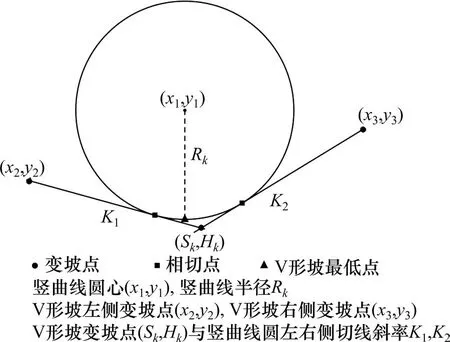
图7 最低变坡点求交示意图Fig.7 Schematic diagram of the lowest vertical intersection point
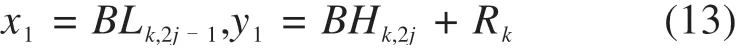
据半径和圆心可确定竖曲线圆,过变坡点(x2,y2)与(x3,y3)可求解与该圆相切的2条切线斜率K1与K2,并根据直线相交,快速计算目标变坡点(Sk,Hk)。
过点(x2,y2)与竖曲线圆相切的直线斜率K1根据式(14)确定:

根据图7所示几何关系,K1取值应为非正值中的较大值,表示最接近V形坡最低点的坡度值。同理可得,过变坡点(x3,y3)的切线斜率K2,此时K2应取非负值中的较小值才具有实际工程意义。
对K1及K2进行整合可得统一表达式:
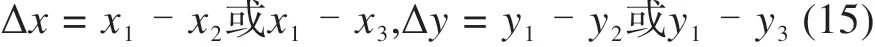
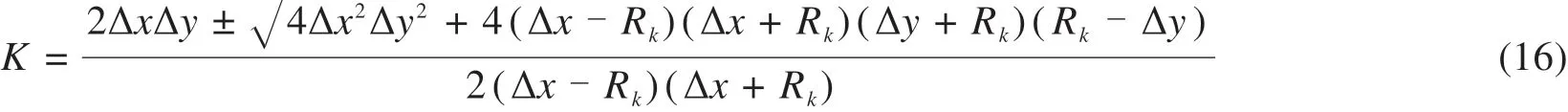
根据图7所示最低点两侧变坡点位置确定K1及K2取值,可得两侧坡段所在直线表达式:

则2条直线交点即为变坡点(Sk,Hk):
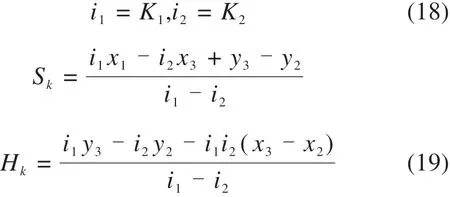
式(13)~(19)展示了获取单位区间单个V形坡变坡点数据的过程,为进一步提高求解效率,利用二线V形坡约束控制矩阵Bm×2n,按式(13)快速构建全线V形坡竖曲线圆心矩阵Om×n。

依据竖曲线圆心矩阵Om×n与各V形坡两侧相邻变坡点,可实现对二线各单位区间V形坡变坡点数据的批量计算与更新,使快速满足合设横向联络通道与泵房约束。但调整会导致V形坡两侧坡段坡度与坡段长度发生变化,对此,引入负反馈机制进行调整,返回图3所示第2阶段进行迭代检测,最终自动生成满足1.1及1.2各项约束的地铁二线纵断面方案。
3 算例验证
本文以厦门地铁6号线为例,自龙江明珠站—新店仔站,全长57 km,以全线40个车站中心为界,可划分为39个单位区间。为详细介绍负反馈线性转化求交法的流程与优势,本文研发了结合ObjectARX编程,采用自定义实体技术对Auto‐CAD进行二次开发的原型系统,基于上述方法分别构建地铁基线与二线实体,以社头站—林埭西站单位区间为研究区间,对地铁二线纵断面自动生成过程进行解析。
3.1 纵断面坡段约束调整
研究区间基线纵断面方案如图8所示,长约3 094 m,共计5个变坡点。由于区间内存在2个连续V形变坡点,构成W形坡,则在该区间内为满足合设横向联络通道及泵房约束,需要结合A~E5个变坡点进行调整,其最终调整目标即按式(6)~(8)计算所得最低点轨面高程:
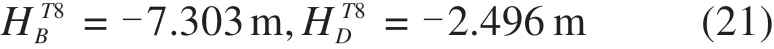

图8 基线纵断面方案Fig.8 Baseline profile scheme
按图3所示调整流程,首先生成如图9所示二线初始纵断面,标红部分坡段长,坡度值方面与基线纵断面表现出直观的差异。然后依据规范对常规约束进行检测与调整,自动生成图10所示纵断面,对满足坡段长度要求的各坡段进行坡度调整,使之满足竖曲线设置要求:

图9 二线初始纵断面Fig.9 Initial profile of second-line
如图10所示纵断面,车站坡段坡度值与基线呈现较大差异,为满足站台范围轨面平行等高约束,需按2.3.2所述对车站段进行调整,结果如图11所示。在保持纵断面初步调整成果的基础上,实现了与二线车站相关坡段坡度值的调整。此时,图11所示各V形坡最低点轨面高程:

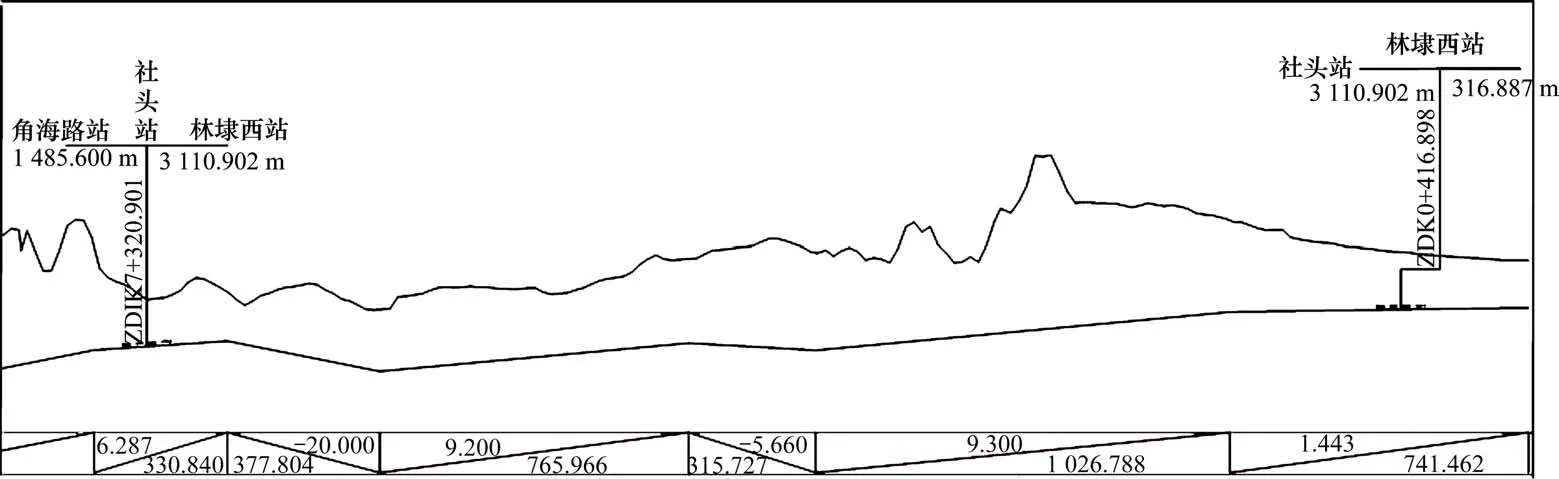
图10 顾及常规约束初步调整纵断面Fig.10 Preliminary adjustment of longitudinal section with conventional constraints
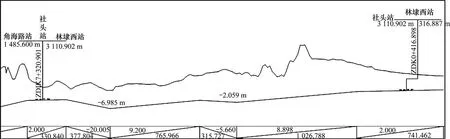
图11 车站坡段调整Fig.11 Adjustment of station slope
与式(21)V形坡B,D最低点轨面高程数据相比,误差达到分米级,必须按照2.3.2调整原则对V形坡变坡点进行调整。W形坡在人工调整时存在坡段间耦合约束,难以达到工程运用要求,新方法以V形坡为基础,将W形坡,甚至多个V形坡组成的广义W形坡视为分段V形坡,固定V形坡两端相邻变坡点,采用分段线性求交的思想,实现对广义W形坡的分段处理,生成图12所示,满足增强约束条件的纵断面。
此时二线V形坡变坡点B,D最低点轨面高程如下:
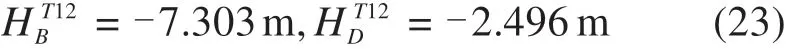
结果表明,V形坡最低点轨面高程,完全满足区间合设横向联络通道及泵房约束。
最后,为保证最终方案合理有效,引入负反馈机制再次进行约束检测,成功则以图12纵断面作为自动设计方案为设计者提供参考,否则返回图3所示第2阶段进行迭代调整,以达到最终要求。
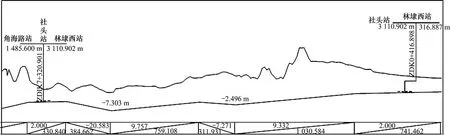
图12 满足增强约束条件纵断面Fig.12 Vertical alignment meeting the enhanced constraints
3.2 平面投影关系调整
式(10)所示平面投影映射关系,可根据基线及二线平面方案,如图13所示得到直接检核。至此,基线与二线平纵断面满足了《地铁设计规范》[7]的常规约束及重要工点定位的增强约束的要求。
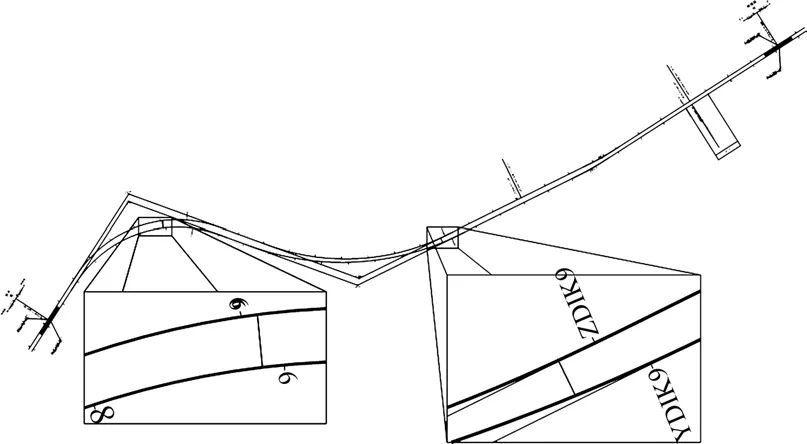
图13 社头—林埭西区间平面方案Fig.13 Horizontal alignment of Shetou-Lindai west area
4 结论
1)建立了纵面几何线形常规约束调整算法,可参照设计基线纵断面,自动生成符合规范几何常规约束的二线初始纵断面。
2)建立了站台范围二线与基线轨面平行等高约束的数学表达,并制定坡度调整策略,实现了双线站台范围内的自动平行等高纵断面设计。
3)推导V形坡与竖曲线的几何调整关系,并提出了广义W形坡分段处理思想,据此构建了分坡段调整策略,破解了基线与二线横向联络通道及泵房自动联合设置难题。
4)基于本文的理论与方法,研发了轨道交通二线纵坡自动生成模块。实例表明该方法可实现常规及增强等复杂约束条件下二线纵坡方案的自动生成,使设计人员摆脱繁琐的二线坡段调整,显著提高了设计效率。

