汽车动力作用对曲线梁桥地震反应特性的影响分析

钟以琛，李岩，叶长允，马小龙，林国伟

(1.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨150090；2.美国康涅狄格大学 土木与环境工程系，康涅狄格州06269-3037；3.济南城建集团有限公司，山东 济南250000)

近年来，我国城市和公路交通基础设施增长迅速，汽车保有量的大幅增长加剧了城市及干线公路的交通压力，特别是高峰时段，城市道路拥堵及大密度车流现象随处可见[1]。桥梁作为交通基础设施的重要组成部分，当某一区域发生地震时，桥上有运营车辆作用的概率较以往大幅增加[2]。现有地震-车辆-桥梁相互作用研究主要集中在铁路桥梁方面，重点关注地震作用下的铁路桥梁横向响应、运营列车舒适性和安全性[3−5]。截止目前，有关车辆作用对公路桥梁地震反应影响的相关研究还很少[6]。各国规范中仅AASHTO和美国加州桥梁设计规范建议在特殊和非常规桥梁地震分析中考虑部分车辆活载的作用，但未给出明确的细化规定[7]。车辆是一个复杂的多体动力系统，其与桥梁发生动力相互作用，会造成车桥耦合体系与单座桥梁的地震响应存在明显差异[8]。KAMEDA等[9]通过数值模拟，发现桥梁与车辆振动频率相近或相位相同时，车辆作用对桥梁地震响应产生不利影响；OTSUKA等[10]针对一座2跨简支梁桥的研究表明，考虑车辆荷载时桥梁地震响应中的横桥向位移和墩底延性需求分别增大15%和20%。GHOSH等[11]提出一种考虑车辆荷载和地震联合作用的桥梁易损性评估方法，发现车辆作用对桥梁震后易损性有较大影响[12]。综合既有研究发现，车辆对桥梁地震作用下的动力响应可产生不利影响，但其规律和机理尚不清晰[12]。目前，相关研究主要集中于常规直线桥，对车载动力性能和地震反应特性都更为复杂的曲线梁桥领域，尚未涉及，鲜有研究。曲线梁桥空间力学特性复杂，弯扭耦合效应突出，车辆作用对桥梁上部结构的倾覆、扭转、爬移等效应具有重要影响，易与结构地震反应形成耦合效应，放大地震响应甚至导致非对称的震害后果[13]。本文建立考虑地震作用的曲线梁桥车桥振动分析模型，依托桥例采用线性时程分析方法，考虑地震动输入方向、车重、车速、地震动峰值、场地类别等参数，研究移动车辆动力作用对桥梁地震反应的影响，为曲线梁桥抗震设计提供理论分析和借鉴参考。

1 地震作用下曲线梁桥车桥振动分析模型

1.1 车辆模型

以公路桥梁荷载试验常用的三轴重型卡车为例，建立车辆分析模型(如图1所示)。车辆模型含16个自由度，其详细参数见文献[14]。

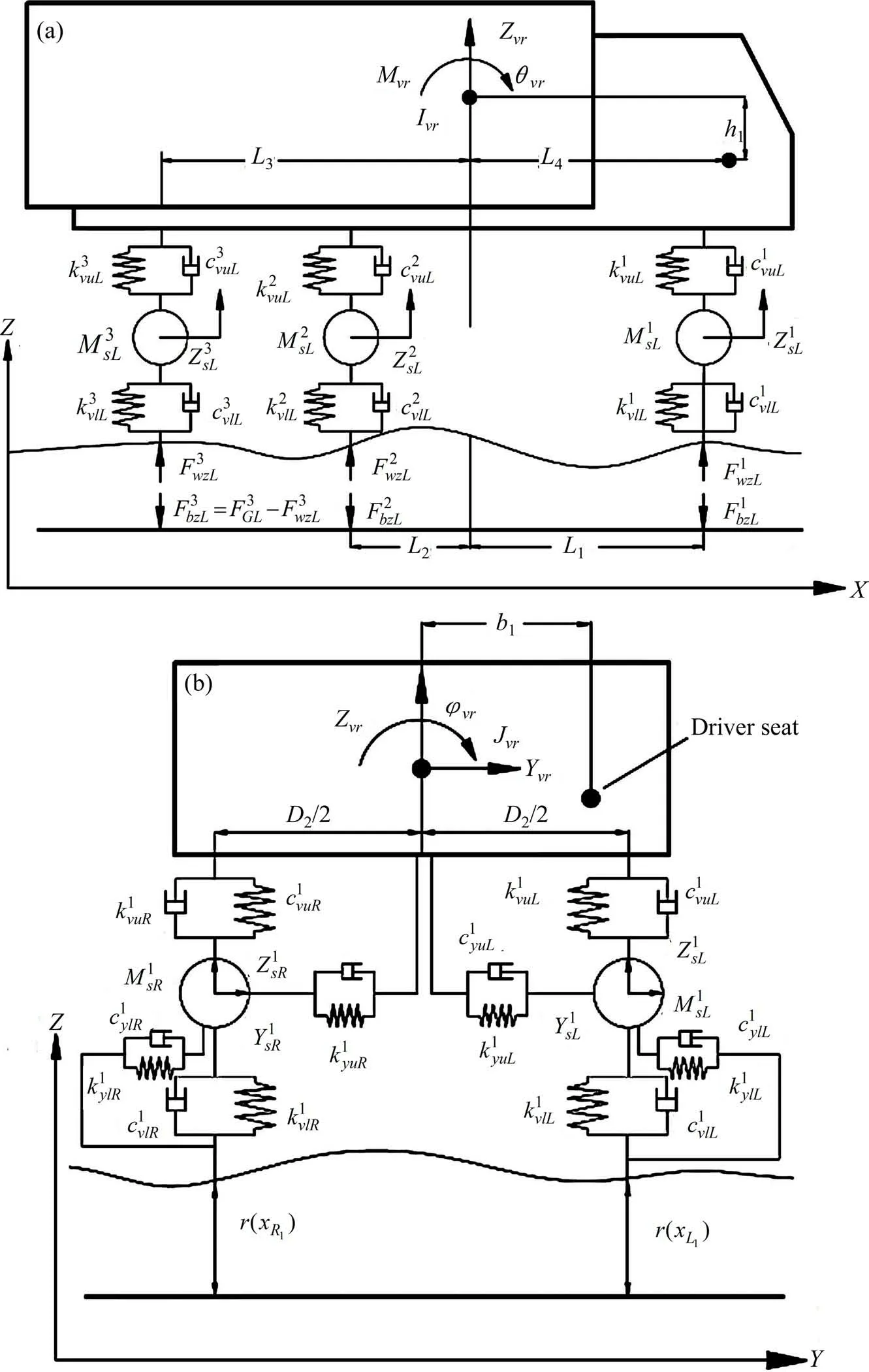
图1 车辆模型Fig.1 Vehicle model

1.2 桥梁分析模型及桥面不平度

采用模态综合技术建立桥梁动力分析模型，利用通用有限元软件建立桥梁空间有限元模型进行模态分析，提取结构振型和频率等模态信息用于后继的桥梁动力行为分析，有关桥梁动力分析模型详细过程见参考文献[15]。

桥面不平度对车桥动力响应有显著影响，本文选取合适的功率谱密度函数，对其进行傅里叶逆变换，得到模拟的桥面不平度。平整度系数参照国际标准化组织(ISO)划分标准，具体过程见文献[16]。

1.3 曲线梁桥车桥耦合振动分析模型

采用整体法，通过车桥接触点的受力平衡及位移协调条件，建立车桥耦合系统动力方程：

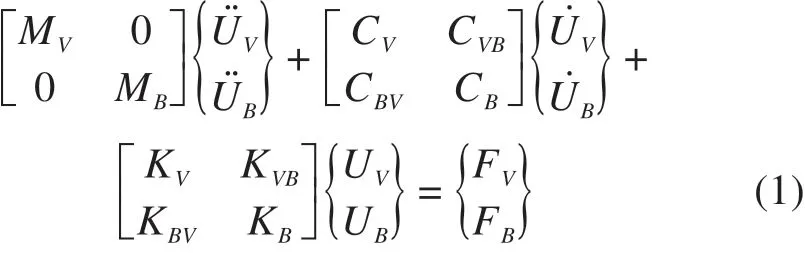
式中：[M]，[C]，[K]分别表示质量、阻尼和刚度项；{U}为位移项；{F}表示荷载项；下标“B”和“V”分别表示桥梁和车辆相关参数；“BV”和“VB”表示车桥耦合项。

曲线梁桥车桥耦合振动分析模型中，整体坐标系和局部坐标系不同，需进行坐标转换。在计算分析时，首先将整体坐标系下桥梁各阶振型分量、车辆参数矩阵等映射到局部坐标系下，在局部坐标中进行车桥动力分析，获得动力响应，然后将计算结果转换到整体坐标系。如图2所示，XB为整体坐标，X−Y表示局部坐标。以桥梁在车辆第i轴左侧车轮处位置为例，桥梁振型分量坐标转换方法如下：

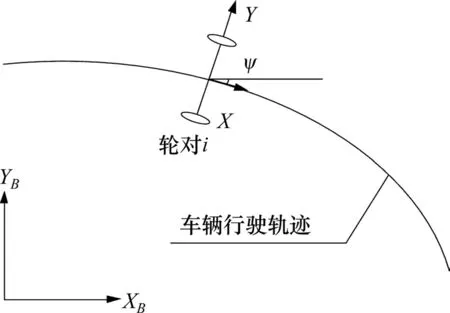
图2 车桥系统坐标系Fig.2 Vehicle-bridge system coordinate

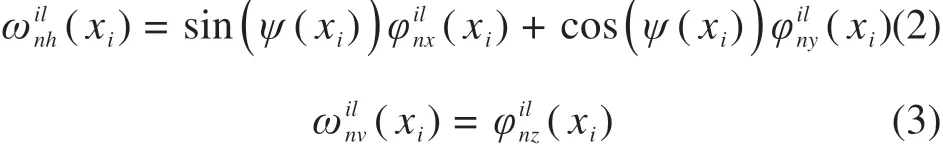
车辆在桥上沿曲线轨迹运动，使车辆受到离心力作用，车体向一侧倾斜，导致两侧车轮力不同(如图3所示)，需对两侧车轮荷载考虑重新分配。其中分别表示该车轮受到作用力横向和竖向分量；θ是桥面与局部坐标y轴方向夹角；h0表示汽车质心与转动重心的间距；mv表示汽车重量。以上车桥振动方程涉及的各项参数具体表达式详见文献[17]。

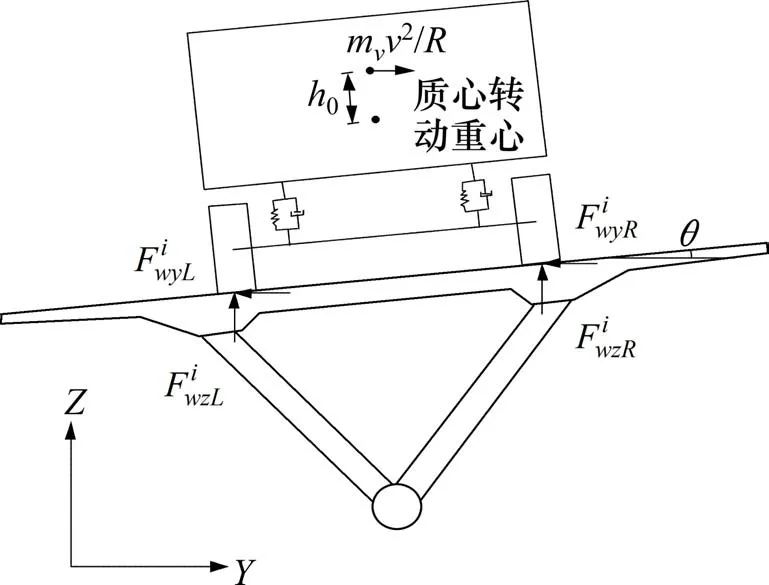
图3 车辆离心力Fig.3 Vehicle centrifugal force

1.4 地震作用下曲线梁桥车桥系统分析模型

基于前述车桥耦合振动运动方程，在其右端添加地震动广义力项，建立考虑地震作用的车桥耦合系统动力方程如下：

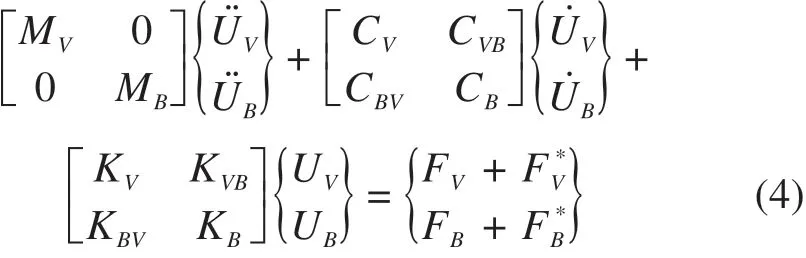
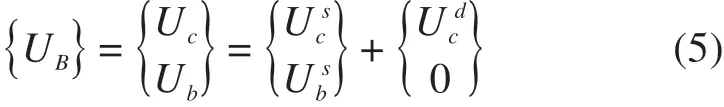
式中：上标“s”，“d”分别表示桥梁拟静力位移部分和动位移部分；下标“b”，“c”分别表示桥梁支承处和非支承处。可通过已知的地震动输入计算获得；当结构参数确定时，也可通过计算获得。假设各边界点激励一致，对模型输入地震动激励。

对于车辆子系统，Nv辆车的地震力表示为：

以前述三轴重车为例，则局部坐标系下第i辆车的地震力向量可表达为：

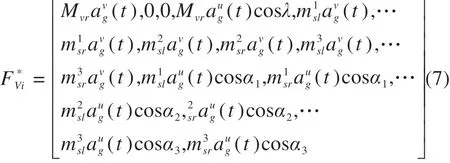
式中：Mvr为车体质量；λ表示车辆轴向与水平地震动输入方向夹角；分别表示第i轴左轮和右轮重量；分别为地震动竖向和横向加速度。αi为水平地震动输入方向与车辆第i轴轴向夹角。

桥梁广义地震力向量可表达为：

式中：Nm是分析过程中考虑的模态阶数。其中为：

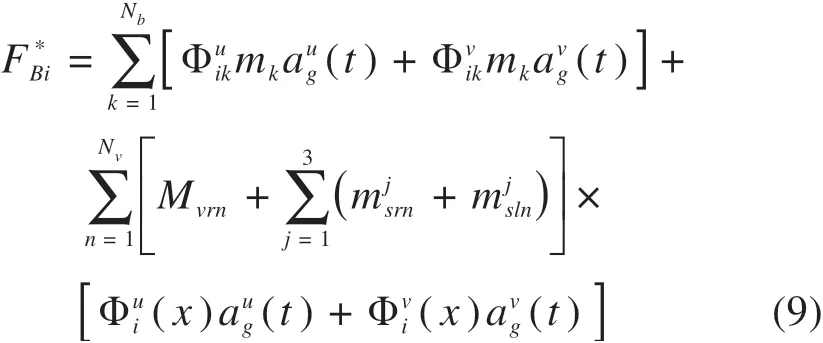
常用的通用有限元软件进行结构动力响应分析时，一般定义振型参与系数为：

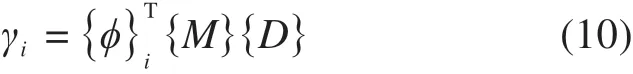
由此，式(9)中桥梁受到的第i阶广义地震力的第1项可简化为：

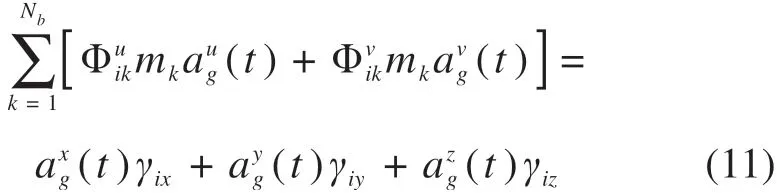
依据以上建立的考虑地震作用车桥耦合振动模型，编制计算分析程序，通过一座曲线梁桥的跑车试验数据和一座曲线梁桥缩尺模型振动台试验数据对所提出的方法和程序进行了间接验证，详见参考文献[18]。

2 移动车辆作用对曲线桥地震反应影响分析

2.1 基本分析参数

以一座4×40 m的曲线连续梁桥为研究对象，进行考虑车辆作用的桥梁地震反应分析。该桥曲率半径100 m，主梁截面为单箱双室，顶、底板宽度分别为12 m和7.5 m，梁高2.2 m；顶、底板厚度自跨中至端部为0.25～0.45 m，腹板厚度0.5 m；两侧悬臂长2.25 m，悬臂厚度自端部至根部为0.15～0.25 m；主梁为C40混凝土。下部结构采用双圆柱墩，其中1号、5号墩直径2 m，墩高17 m；2号、4号墩直径1.5 m，墩高20 m；3号墩直径1.5 m，墩高25 m。3号墩设有横系梁，系梁截面为1.2 m×1 m，长6 m。桥墩盖梁截面为1.6 m×1.7 m，长10.7 m。桥墩及盖梁均采用C30混凝土。3号墩布置固定支座，其余墩为单向滑动支座。

采用ANSYS建立该桥空间有限元模型，其中主梁、盖梁及桥墩选用SOLID65实体单元，支座为COMBIN14弹簧单元。模型如图4所示。

图4 曲线梁桥有限元模型Fig.4 Finite element model of curved bridge

基于自编的动力分析程序，依托该桥例，考虑移动车辆参数和地震动参数变化，针对移动车辆作用对桥梁地震动力响应的影响，开展了分析研究，方法流程如图5所示。

图5 车辆作用下曲线梁桥地震响应分析流程图Fig.5 Flow chart of curved bridge seismic response analysis under vehicle loads

2.2 车辆作用对曲线梁桥地震反应的影响

选取曲线梁桥各桥墩连线和垂线方向作为输入方向，每个方向均考虑3种典型地震波进行分析。3条地震波如图6所示，其中NGA-172、NGA-1338和NGA-2107分别取场地类别Ⅲ，Ⅱ和Ⅰ。考虑一辆总重30 t 3轴整车，以车速60 km/h沿桥梁轴线行驶过桥，车辆参数见参考文献[17]。

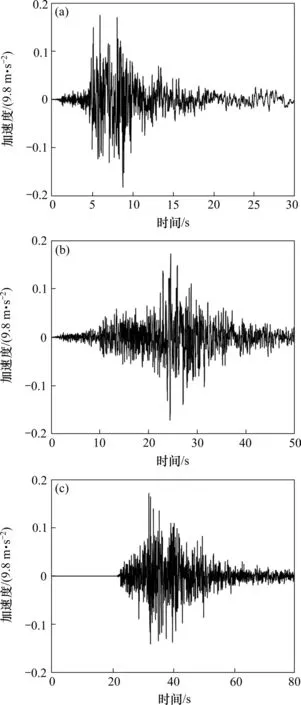
图6 地震动时程Fig.6 Time histories of ground motion

考虑各工况有车和无车情况，以上、下支座板的相对位移(后简称支座相对位移)，及墩底剪力为对象进行分析。发现支座最大相对位移多发生在1号墩处，墩底最大剪力发生在3号墩处(如图7和图8，其中“1-2连”代表地震动输入方向为1号墩、2号墩连线方向，“1-2垂”代表与1号墩和2号墩连线相垂直方向)。

由图7可知，支座切向相对位移较径向更为显著，且不同地震波对其影响差异较大，其中NGA-172作用下支座相对位移最大，NGA-2107作用下最小。不同地震波下移动车辆对桥梁地震响应的影响不同，其中NGA-172作用下车辆对地震响应影响较大。

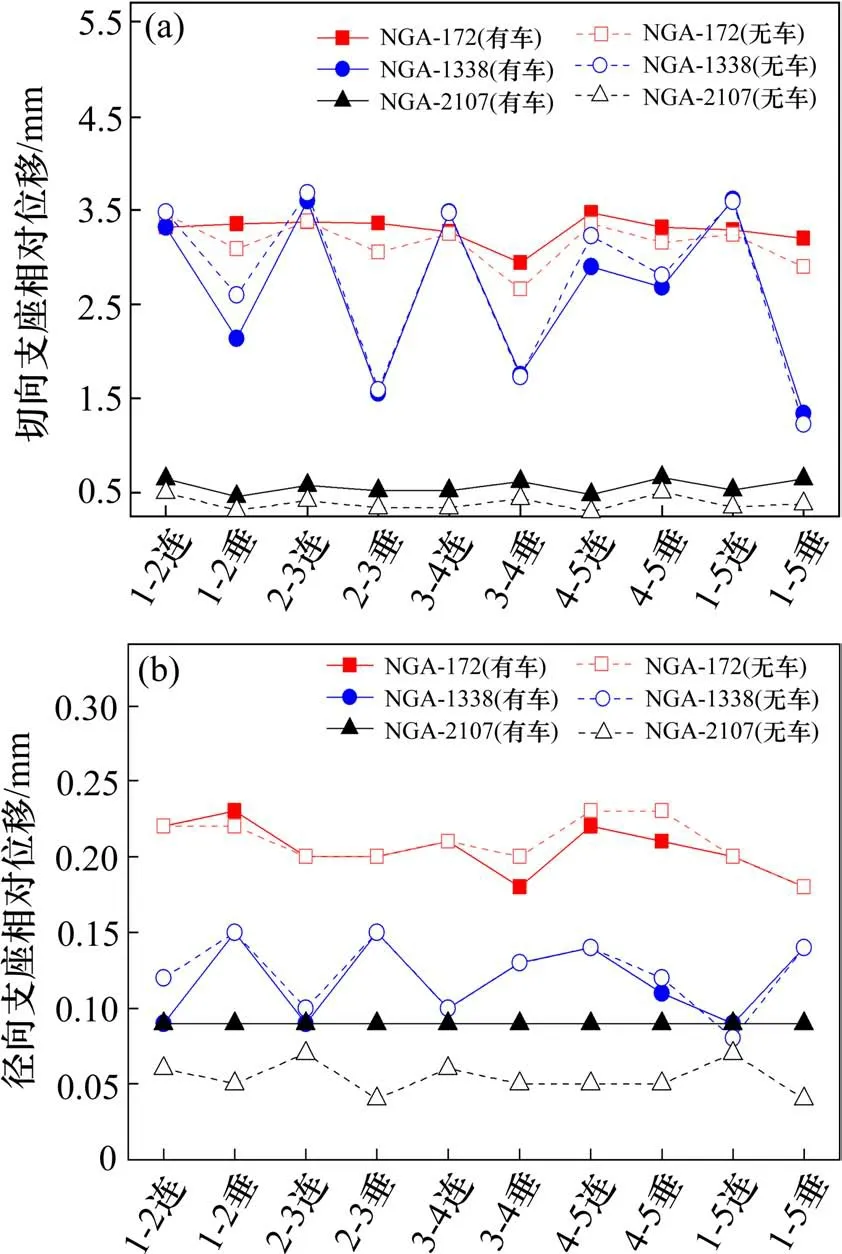
图7 车辆作用对支座相对位移影响Fig.7 Vehicle effects on bearing displacement

由图8可见，各工况下径向墩底剪力大于切向。车辆对桥梁地震响应的影响在不同地震动类型下有较大区别，其中NGA-172和NGA-2107作用下车辆作用对墩底剪力有放大作用，最大增幅为33.75 kN，NGA-1338作用下移动车辆作用会削弱墩底剪力22.71 kN，相对无车状况降低9.25%。

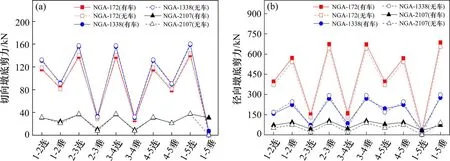
图8 车辆作用对墩底剪力的影响Fig.8 Vehicle effects on shear force of pier bottoms

综上所述，地震波NGA-172下结构地震响应最不利，故后继考虑各参数对车辆作用下桥梁地震响应影响分析时将其作为激励源，地震动激励方向分别取1号墩～5号墩连线(0°)和垂线(90°)。

2.3 车辆关键参数对桥梁地震响应的影响

2.3.1 车重的影响分析

分别选取车重为0(无车情况)，20，30，40和50 t的3轴重车以60 km/h车速过桥，地震动选取NGA-172，输入方向为0°和90°进行分析，结果如图9所示。

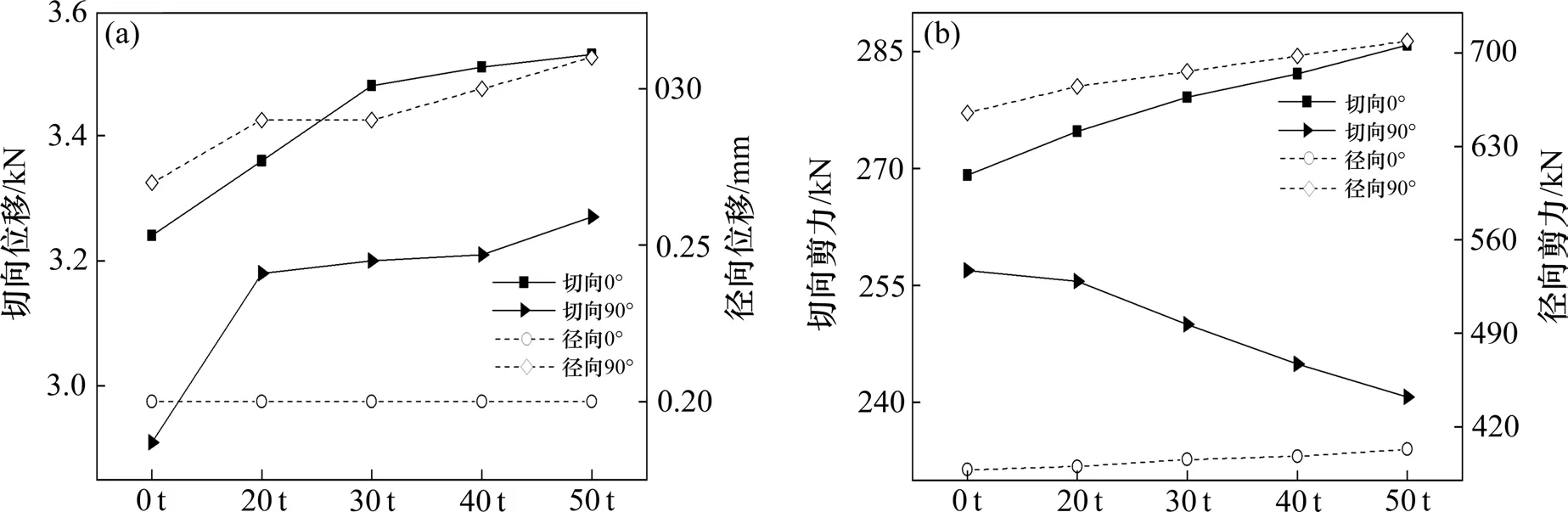
图9 车重对曲线梁桥地震响应的影响Fig.9 Effects of vehicle weight on bridge seismic responses

可见，各车重下支座最大相对位移位于5号墩处，最大墩底剪力发生在3号墩处。随车重增加，地震作用下支座相对位移和墩底剪力呈逐渐增加趋势。车重50 t时，各工况下支座相对位移峰值达3.53 mm，墩底剪力峰值达708.88 kN，相对无车状况分别增幅8.95%和8.21%。这是因为结构受到车辆作用增加，进而使与地震波同向的桥梁响应增大。

2.3.2 过桥车速的影响分析

考虑车重30 t的3轴车以车速30，40，50和60 km/h过桥，地震动选取NGA-172，输入方向分别为0°和90°，并对照无车状况(0 km/h)进行分析。结果如图10所示，各车速工况下最大支座相对位移多发生在5号墩处，最大墩底剪力多发生在3号墩处。

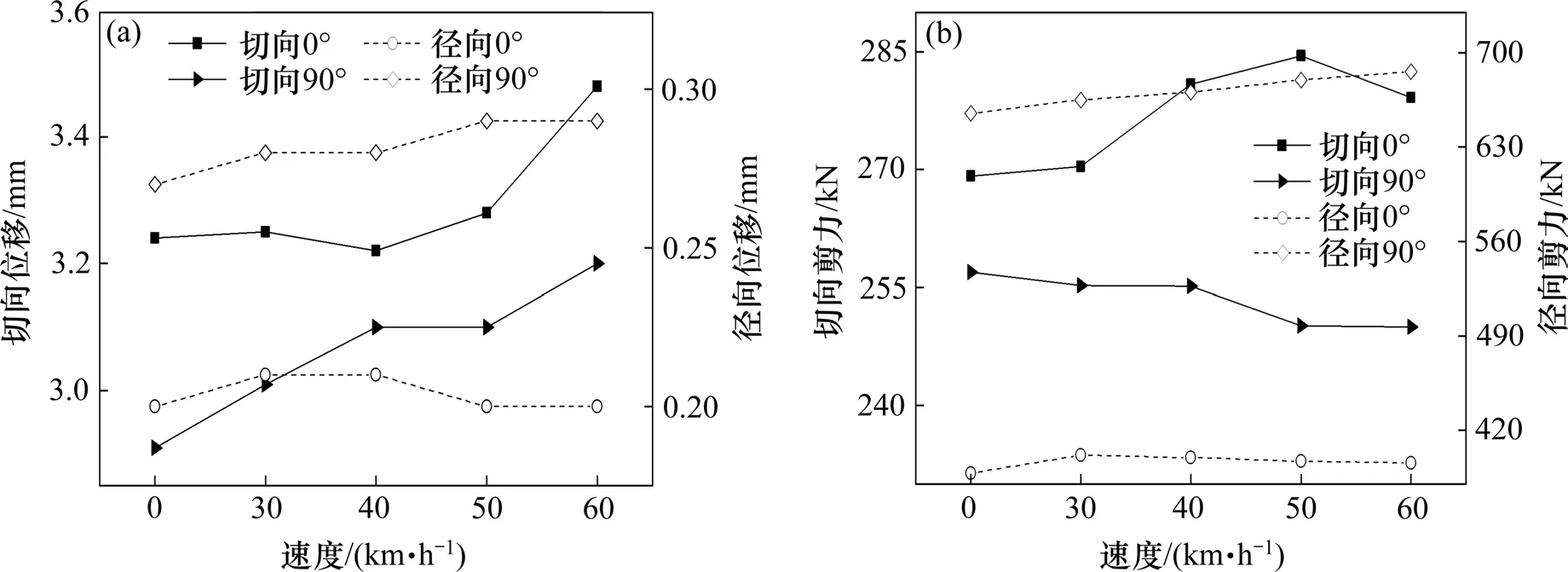
图10 车速对曲线梁桥地震响应的影响Fig.10 Effects of vehicle speed on bridge seismic responses

结果表明，地震波输入角度0°时，随车速增加切向地震响应呈增加趋势，径向响应峰值发生在30 km/h附近；当地震波输入角度90°时，随车速增加径向的地震响应呈增加趋势，而车辆作用会减弱切向墩底剪力。可见车辆速度参数对结构地震响应的影响较为复杂，分析认为主要由于车速变化导致移动荷载对桥梁激振频率改变，使得曲线梁桥动力响应发生变化。

2.4 地震动参数对桥梁地震响应的影响分析

2.4.1 地震动峰值的影响分析

车辆模型取车重30 t，车速60 km/h。地震动选取NGA-172，输入方向为0°和90°，修改地震动峰值分别为0.1g，0.2g和0.4g，分别对应抗震设防烈度7度、8度和9度，进行地震反应分析。如表1和表2所示，不同地震动峰值下最大支座相对位移均发生在1号墩处，最大墩底剪力发生在3号墩处。

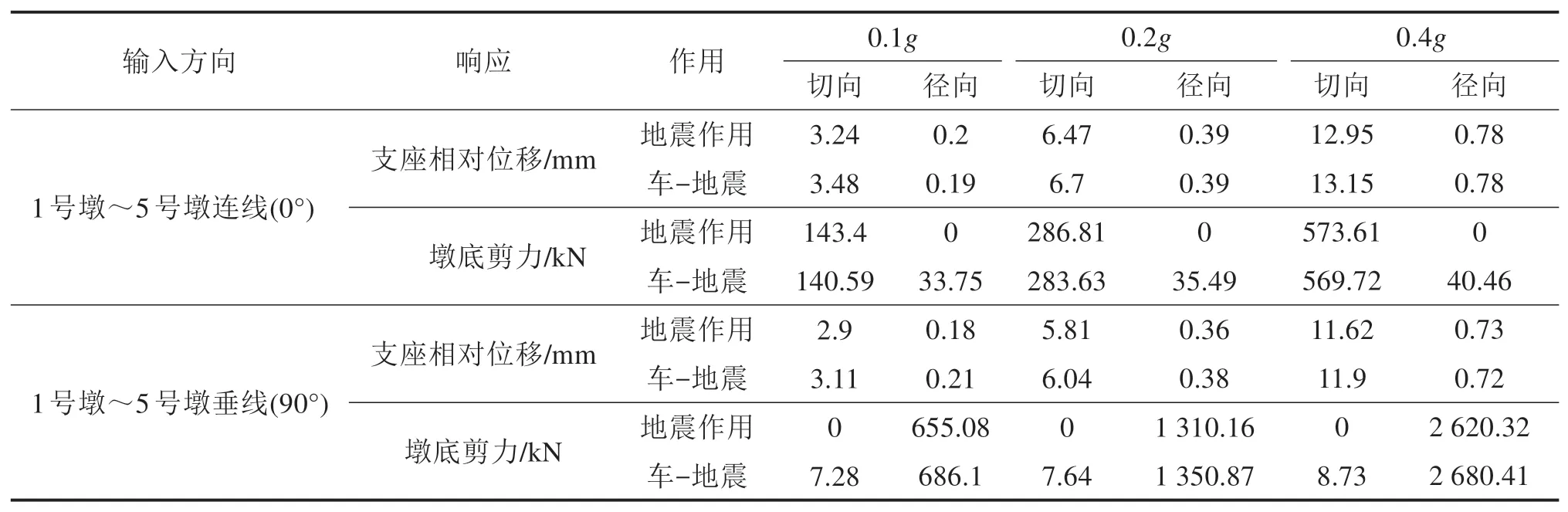
表1 不同地震动峰值作用下桥梁的最大地震响应比较Table 1 Bridge maximum seismic responses under different peak values of ground motion

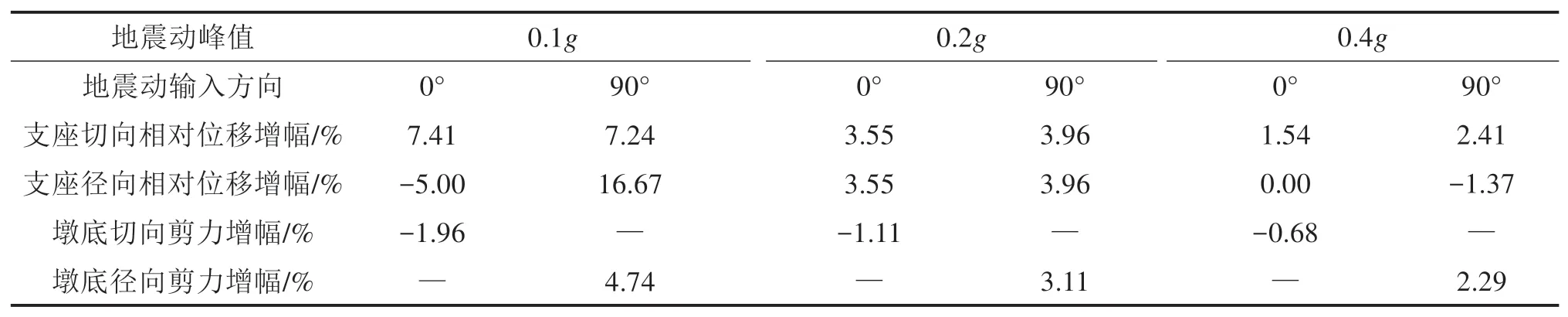
表2 不同地震动峰值作用下车辆对桥梁地震响应的影响Table 2 Effect of vehicle load on bridge seismic responses under different peak values of ground motion

结果表明，随地震动峰值增加，移动车辆作用对桥梁地震响应的影响减弱，地震峰值0.4g时，支座相对位移较无车时增幅少于2.41%，墩底剪力增幅少于2.29%。表明地震峰值增加到一定程度时，可不考虑车辆作用对曲线梁桥地震响应的影响。

2.4.2 场地变化影响分析

车辆参数同前，选取场地类别Ⅰ，Ⅱ和Ⅲ，输入角度分别为0°和90°合成地震波，其中加速度峰值取0.1g，持续时间12 s，进行桥例的地震反应分析。结果如表3和表4所示。

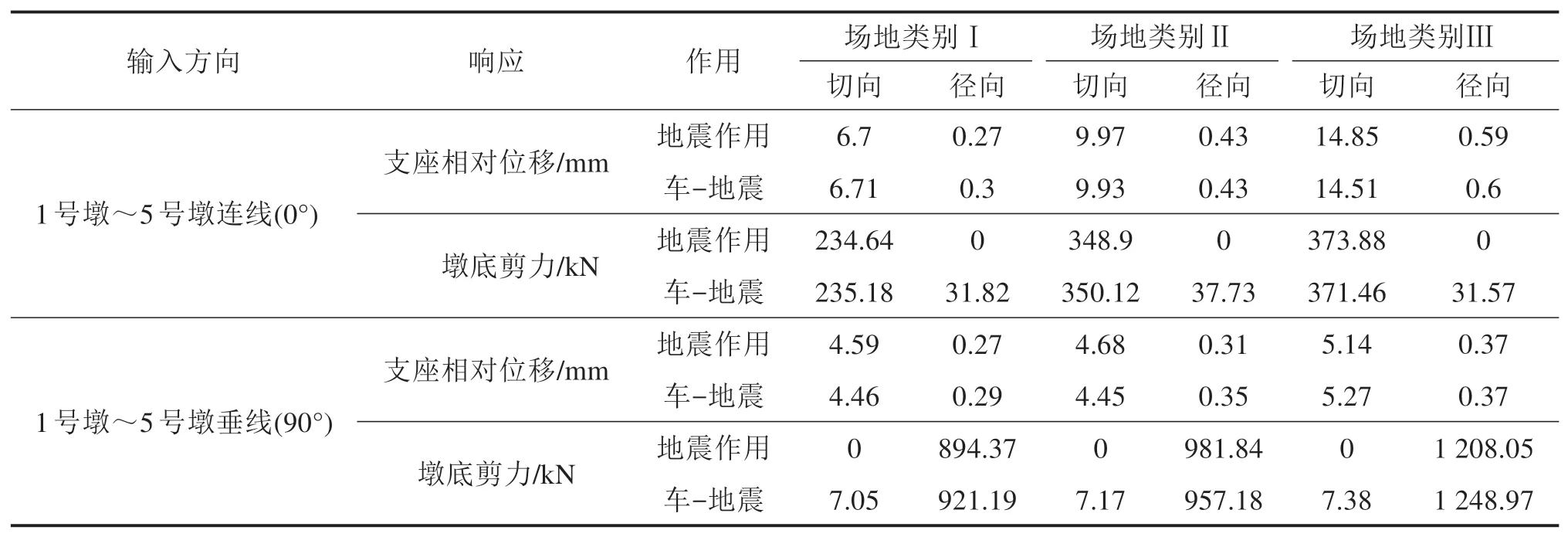
表3 不同场地类别下桥梁最大地震动力响应比较Table 3 Bridge maximum seismic responses under various site conditions

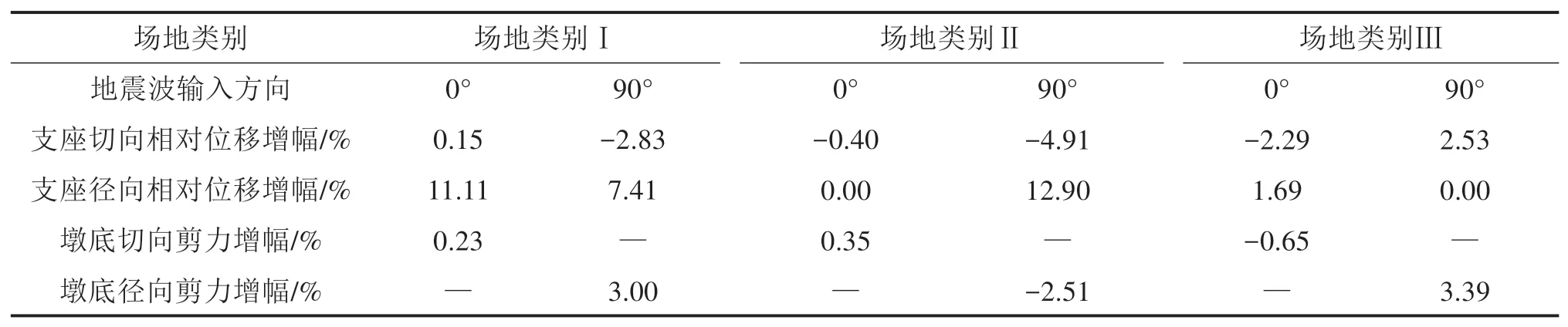
表4 不同场地类别下车辆对地震响应的影响Table 4 Effect of vehicle load on seismic responses under various site conditions

结果表明，选取地震波场地类别为Ⅰ或Ⅲ时，考虑车辆作用会增加结构的地震响应，其中支座相对位移最大增加12.9%，墩底剪力增幅3.39%。在地震波场地类别Ⅱ时，考虑车辆影响将削弱结构地震响应。对场地类别做频谱分析，发现场地类别Ⅰ下地震波频率集中在3～4 Hz，与桥梁横向一阶频率(3.92 Hz)相近；场地类别Ⅱ下地震波频率分布范围较宽，为0～4 Hz；场地类别Ⅲ下地震波频率集中在1～2 Hz。可见地震波频率分布较宽时，车辆作用对桥梁地震反应影响较小；地震波频率集中，尤其相近于桥梁横向1阶频率时，车辆对桥梁地震反应的影响较大。

3 结论

1)提出了考虑地震作用的曲线梁桥车桥振动分析模型，为抗震研究提供了理论基础和方法借鉴。

2)不同地震波作用下，移动车辆对曲线梁桥地震反应的影响存在较大差异，车辆对桥梁部分地震响应增幅可达16.67%。其中，支座切向相对位移增幅一般大于径向，墩底切向剪力一般小于径向；曲线梁桥抗震分析考虑车辆作用的不利影响十分必要。

3)车重和车速的增加导致移动车辆作用对曲线梁桥地震反应的影响增大，运营中应针对性对地震高发地区车辆行驶提出限速、限重要求。

4)提高震动峰值，结构地震反应受到车辆的影响变小，当地震峰值为0.4g时，支座相对位移较无车时增幅少于2.41%，墩底剪力增幅少于2.29%。针对高设防烈度地区进行桥梁抗震设计时，可不考虑车辆作用的影响。

5)不同场地条件下车辆作用对桥梁地震反应的影响存在明显差异，地震波频率分布集中在3～4 Hz时，其频率与曲线连续梁桥横向一阶频率相近，车辆作用对桥梁地震反应的影响较大。