改进蚁群算法水面无人艇平滑路径规划
敖邦乾 ,杨 莎,叶振环
(1.遵义师范学院工学院,贵州遵义 563006;2.遵义师范学院物理与电子科学学院,贵州遵义 563006)
1 引言
路径规划是所有智能移动系统研究中的一个重要领域,路径的可行性是完成自主移动的首要关键环节,水面无人艇(unmanned surface vessel,USV)是一种可以在海洋当中实现自主航行,并完成相应任务的小型水面船舶,经常被用来执行情报收集、环境监测、海上搜救和水文地理勘查等特殊任务,具有十分广泛的用途,路径规划对于USV有着非常重要的作用,USV不断的与周围环境进行信息交互,并及时更新自己的位置信息.路径规划主要分为两类:全局静态路径规划和局部动态路径规划[1],全局路径规划的算法主要有人工势场法[2]、A*算法[3]、粒子群算法[4]、蚁群算法[5]、遗传算法[6]、神经网络算法[7]、各种改进型算法[8–9]和混合型算法[10–11],其中人工势场法容易陷入局部最优和死锁现象;A*算法会造成不必要的绕远路,得到的并不是最优路径;粒子群算法需要大样本来逼近系统的后验概率,并且重新采样阶段会导致样本有效性和多样性丧失,从而导致样本耗竭,而且算法计算量大;蚁群算法在搜索过程中不可避免的产生大量局部交叉路径,而且大量蚂蚁个体会在搜索最优路径过程中迷失,产生大量的非完整路径;遗传算法在没有实际经验和数据的情况下,遗传算子参数的选取比较困难,适应度值的取值也比较随机;神经网络算法则存在计算量大的问题,在开始阶段需要大量的训练,不适合于计算能力有限的平台.基于上述问题,很多人对环境进行了各种预处理,并对算法进行了改进,巩敦卫等人在文献[12]中通过构造密集障碍物的凸包,采用微粒群优化规划机器人路径,同时在文献[13]中提出多目标模型,并采用粒群算法解决机器人在多地貌环境下的路径规划问题,在文献[14]中更进一步,通过定义隶属度函数来评估路径的风险程度,设计了一种约束多粒子群算法来提高有效性,在文献[15]中提出了一种基于粒子群优化算法的改进集中式算法,仿真结果证明了算法的有效性与可行性.适合于USV行驶的路径必须是满足方位和曲率连续的可行路径,路径的平滑与否是实现精确路径规划的前提,如文献[16]对航路点序列使用三次Hermit样条法进行拟合,且针对航路点处曲率不连续给出了方案,可以生成通过所有航路点的单调曲线,文献[17]则利用非均匀B样条曲线对折线路径的每一个转弯处进行光顺处理,快速构造出方位和曲率均为连续函数的二维路径,但是,很多算法设计的平滑路线,要么是直线与弧线段的拼接,要么是直接利用样条曲线,没有考虑USV的动力学状态,并不是一条适合的最佳可行路径.
本文首先通过对蚁群算法的局部及全局信息素的更新策略进行改进,得到初始航线段,然后对航点进行无障碍优化,最后对生成的折线段进行路径平滑算法设计,使得所生成的曲线路径的方位和曲率均为连续的函数,保证了路径的平滑性及可行性,仿真结果表明提出的算法具有很好的迭代效果,能规划出一条较为优化的平滑可行曲线路径.
2 基本算法描述
对USV从起点到终点的运行环境进行栅格化建模,将环境栅格化为一定数量的栅格,以二值格式对栅格进行编码:1表示当前栅格存在障碍物,0表示无障碍物,每个栅格的属性存储包括障碍物位置、海浪波幅、海流流速、海风风速等信息,然后利用仿生学原理,对障碍物做开运算,建立的模型极大程度上契合实际物理环境,可行空间与障碍物也得到了精细的建模及划分.
2.1 环境建模
形态学以图像的形态特征为研究对象,其基本运算有腐蚀、膨胀,还可以组合出各种其它的形态学算法来对图像进行特征提取、边缘骨架抽取等[18],假设运算对象障碍物图像A和结构元素B(通常是包络图),A关于B的腐蚀和膨胀分别定义为
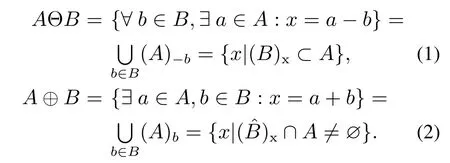
式中:(A)−b是A关于B的映射的平移集合,(A)b是A关于B的平移集合,腐蚀运算删除图像中障碍物边界的某些像素,使目标区域范围变小,可以用来消除那些比较小且无意义的物体,膨胀运算则给图像对象边界添加像素,使目标区域范围变大,将与目标区域接触的背景点合并到该目标中,使目标边界向外部扩张,用来填补物体中的空洞,小且无意义的物体,膨胀运算则给图像对象边界添加像素,使目标区域范围变大,将与目标区域接触的背景点合并到该目标中,使目标边界向外部扩张,用来填补物体中的空洞,有去除噪点[19]的作用,它们的组合有如下2种形式:

式(3)和式(4)分别表示闭运算和开运算,其中,闭运算连接相临近的物体,平滑其边界的同时并不明显的改变其面积;而开运算在细微点处分离物体,平滑较大物体的同时并不明显的改变其面积,并使其成为四边形形状,其模型如图1所示.
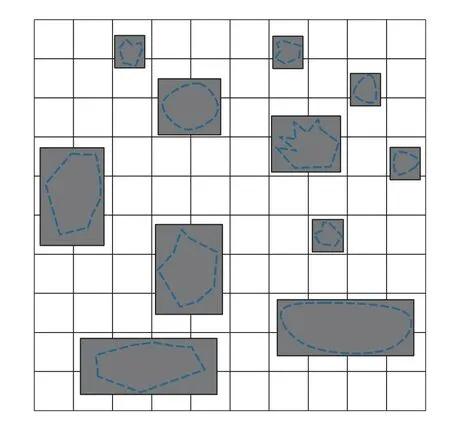
图1 栅格化环境模型Fig.1 Rasterize environment model
经过栅格化建模和对障碍物进行开运算以后,环境障碍物以及USV可行空间得到了精确的划分,在可行区域内,USV下一步的可能航向如图2所示,使用算法获得整个航路段下一步可能的航点,所有航点构成了整个USV的全局航线.
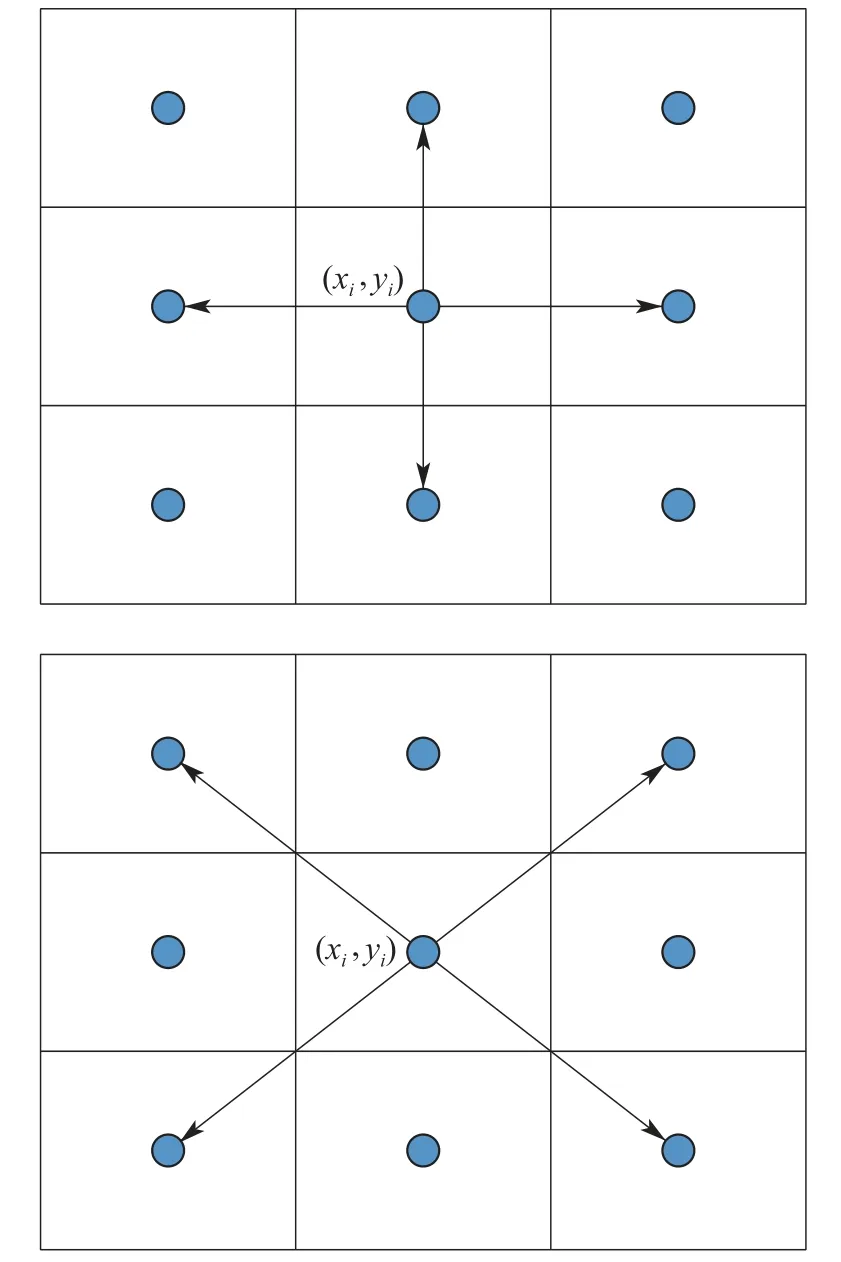
图2 下一步运动规则Fig.2 The next movement rules
2.2 路径算法设计
蚁群算法[20]是一种新型分布式智能仿生类算法,通过模拟蚂蚁觅食过程中蚂蚁群体之间、蚂蚁蚁群与环境之间不停的通过信息交互来实现最优路径的选择,蚂蚁所走的路径越短以及留下的信息素就越多,蚂蚁倾向于选择该路径,路径上的信息素就会越来越多,这样就形成了一个正反馈机制,最后蚁群能找到最优路径,在搜索空间范围比较大的情况下,蚁群算法的优越性更好,路径规划中没有过多的障碍物,信息素的更新比较集中,算法的复杂度进一步得到了降低,该算法首先成功使用在解决旅行商问题上.
本文改进蚁群算法如下:使用GPS(超高灵敏度,更新率1~10 Hz,误差±1 m)定位当前USV在海洋中的位置,同时结合电子罗盘测量的偏转角,规划出一条从起点到终点的全局路线,自定义设置从当前USV位置指向终点目标位置方向为零度方向,罗盘偏离角度为θ(逆时针为正0◦≤θ≤180◦,顺时针为负−180◦≤θ≤0◦),改进蚁群算法如下:
Step 1初始化蚁群参数如信息素启发因子α、期望启发因子β、启发信息诱导因子γ、全局信息素挥发系数ρρ、局部信息素挥发系数ρ等,假设蚁群规模为n,初始化每条边的信息素量值:τij(0)=1,∆τij(0)=0,最大迭代次数为Nmax;
Step 2将蚂蚁放置在当前GPS定位的航迹规划空间的起始点上,设置禁忌表为对应的顶点;
Step 3按照蚂蚁的转移规则和转移概率选择下一个节点:

其中:k为第k只蚂蚁;ψ0(0 ≤ψ0≤1)为可以根据经验得到的固定阈值常数;ψ为均匀分布在[0,1]之间的随机数;τij(t)为第t次迭代时节点i到节点j的路径上的信息素浓度;α(α>0)为信息素启发因子;ηij(t)为第t次迭代时节点i到节点j的路径上的距离启发信息,大小为ηij(t)=1/Lij;Lij为节点i到节点j的路径上的能耗启发信息;β(β >0)为距离启发信息期望启发因子;φij(t)为第t次迭代时节点i到节点j的罗盘偏转角度启发信息,大小为1/|θ|;γ(γ >0)为罗盘偏转角度启发信息诱导因子;
Step 4对每只蚂蚁经过一次一步移动后进行信息素局部更新:
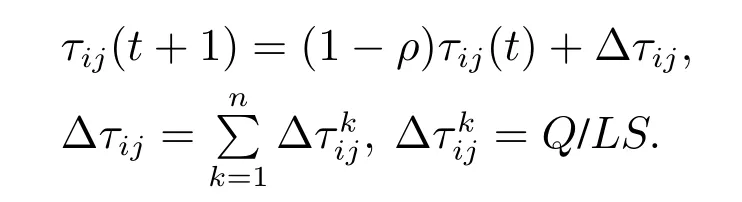
各变量表示如下:τij(t+1)为移动一步后的信息素浓度;τij(t)为当前节点的信息素浓度;ρ(0<ρ<1)为信息素局部更新挥发系数;∆τij(t)为本次循环中各只蚂蚁在路径i →j上留存的信息素浓度;为信息素的改变值;Q为根据经验设置的常数;LS为蚂蚁k在本次循环中所走的总路径航迹综合值.
Step 5更新禁忌表;继续计算概率,再选择节点及更新禁忌表,直到遍历所有节点1次;对所有蚂蚁完成一次迭代后得到的最优路径进行信息素全局更新,同时更新禁忌表:
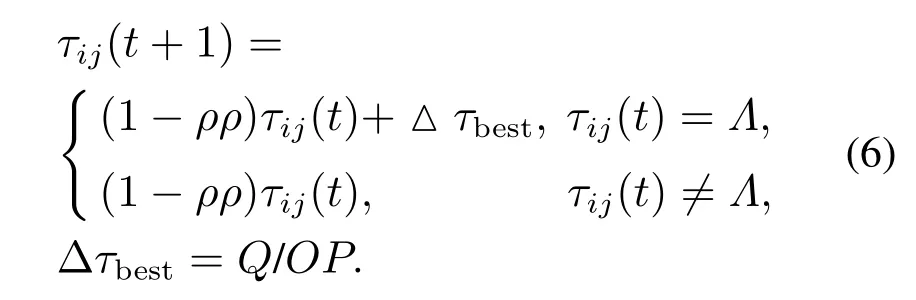
其中:ρρ为信息素全局更新挥发系数;Q为经验常数;OP为本性循环中所得最优路径;Λ为当前得到的最优解.
Step 6计算该只蚂蚁留在各边的信息素量,丢弃该只蚂蚁,进入下一次迭代;
Step 7重复Step 3到Step 6,直至n只蚂蚁都遍历完毕;
Step 8计算各边的信息素增量和信息素总量,记录本次迭代的路径,更新当前的最优路径,清空禁忌表;同时判断是否达到预定的迭代步数Nmax,或者判断是否出现停滞现象,若是,算法结束,输出当前的最优路径;否则,转Step 2,进行下一次迭代.
2.3 算法仿真分析
本算法在CPU 为Inter(R)Core(TM)i7–8750H CPU @2.20 Hz2.21 GHz、Memory为16 GB、GPU为NIVIDA GeForce GTX 1080 Ti、版本号为MATLAB 2016a的平台下进行测试,仿真环境为20×20经过腐蚀处理过的平面栅格模拟环境(如图1),分简单环境及复杂环境下的仿真.
影响蚁群算法性能的参数有很多,而且相互影响,一个值的选择可以影响其它参数,甚至整个算法的优劣性,但是目前还没有合适的数学模型或者数值数理分析方法在每种情况下都能生成最优值,通常情况下只能通过经验来进行参数的选择,本文在设置一定参数变化范围的情况下,通过设置不同的参数组合反复多次的实验结果来选择最优的参数组合,蚁群算法的信息素的浓度和启发信息的大小对本算法具有较大的影响,因此选择与此有关的5个参数:信息素启发因子α、期望启发因子β、启发信息诱导因子γ、全局信息素挥发系数ρρ、局部信息素挥发系数ρ.对这5个重要参数,每个参数选取5个点进行分析,分别为

对每个参数设置一组值,同时其他参数保持不变,并进行10次仿真,对结果求均值进行对比.初始时,设置一组默认参数值为α=1,β=3,γ=10,ρρ=0.3,ρ=0.3,多次仿真实验,可以得到如表1中的数据.
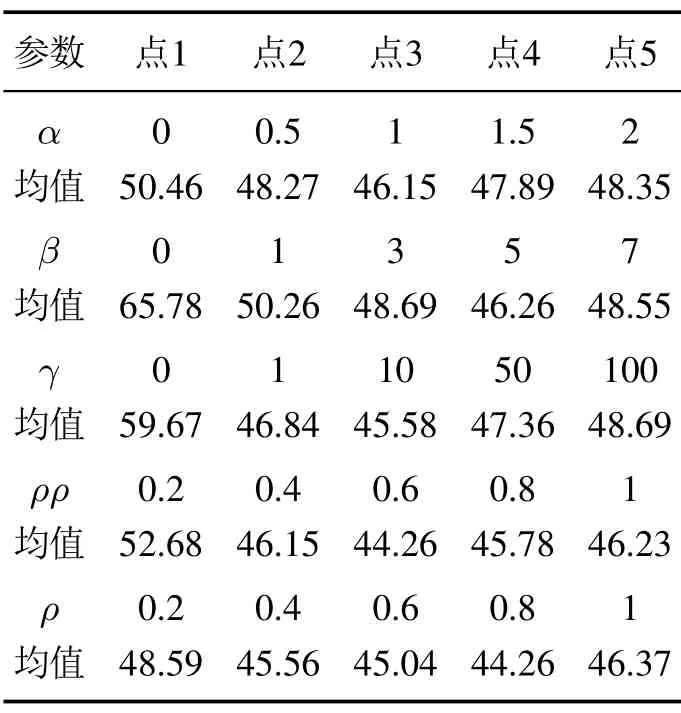
表1 本文算法的参数优化结果Table 1 Parameters optimization of the algorithm
由表1中的参数优化结果,本文算法的主要参数有如下特征:α的优化值大约为1,β的优化值出现在5附近,γ的优化值大约为10,ρρ的优化值处于0.6与0.8之间,ρ的优化值为0.8左右.对于本算法,最终选取的优化值为:α=1,β=5,γ=10,ρρ=0.7,ρ=0.8.同时取值Q=1.
在参数设置完全一致的情况下,将本算法仿真结果同时与基本蚁群算法和势场算法两种算法在路径长短及迭代次数上进行比较,设置起始位置为(20,0),终点位置为(0,20),图3为在较简单及复杂环境下的仿真结果.
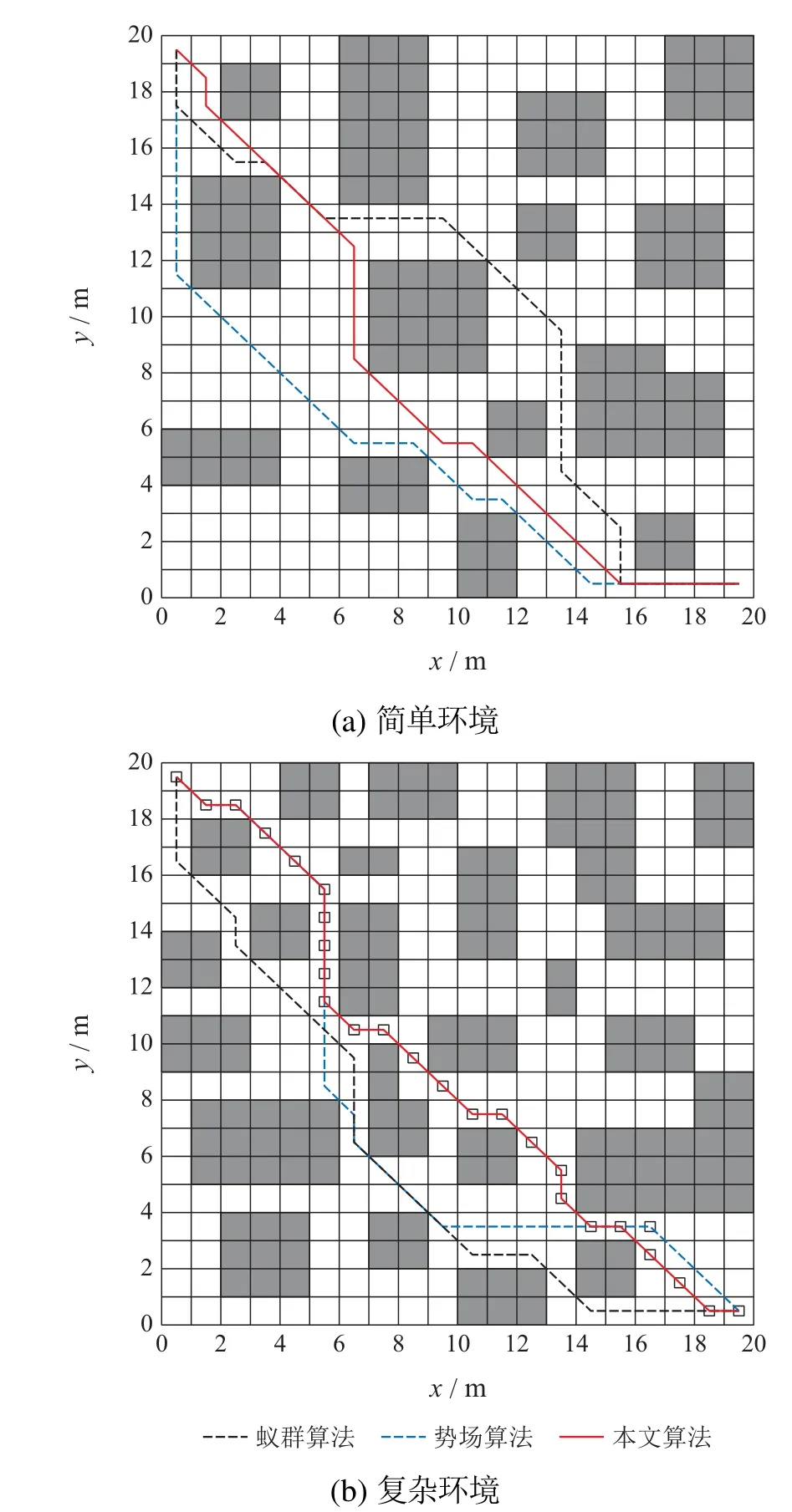
图3 不同环境下3种算法轨迹对比Fig.3 Trajectory comparison in different environment
从图4及表2–3可以看出,不管是简单环境还是复杂环境,3种算法都能收敛得到最终路径,基本蚁群算法搜索到的路径因为容易陷入局部最优的情况,导致其算法收敛的迭代次数要大于其他两种算法,而且其搜寻到的路径长度,也要大于其他两种算法,简单情况下路径长度为31.753 m,复杂环境下则为34.258 m.势场力算法由于为蚁群提供了较为正确的初始启发信息,而且在势场力的正反馈作用下,其收敛速度明显得到了加快,两种环境下迭代次数分别为12次和17次,得出的路径也是一条比较优化的路径,本文算法加入了硬件设备GPS和COMPASS,其相关参数在路径循迹中对信息素有较大的改进,避免了局部最优解,而且在循迹过程中,其方向始终指向终点,因此具有较优的全局搜索性,从3种算法对比结果来看,本文算法在简单环境下只需要经过8次迭代,就能寻得较优的29.837 m的路径长度,复杂环境下经过13次迭代就能得到32.985 m的优化路径,不管是在简单环境下,还是在复杂的环境中,本文算法都有较强的普适性.
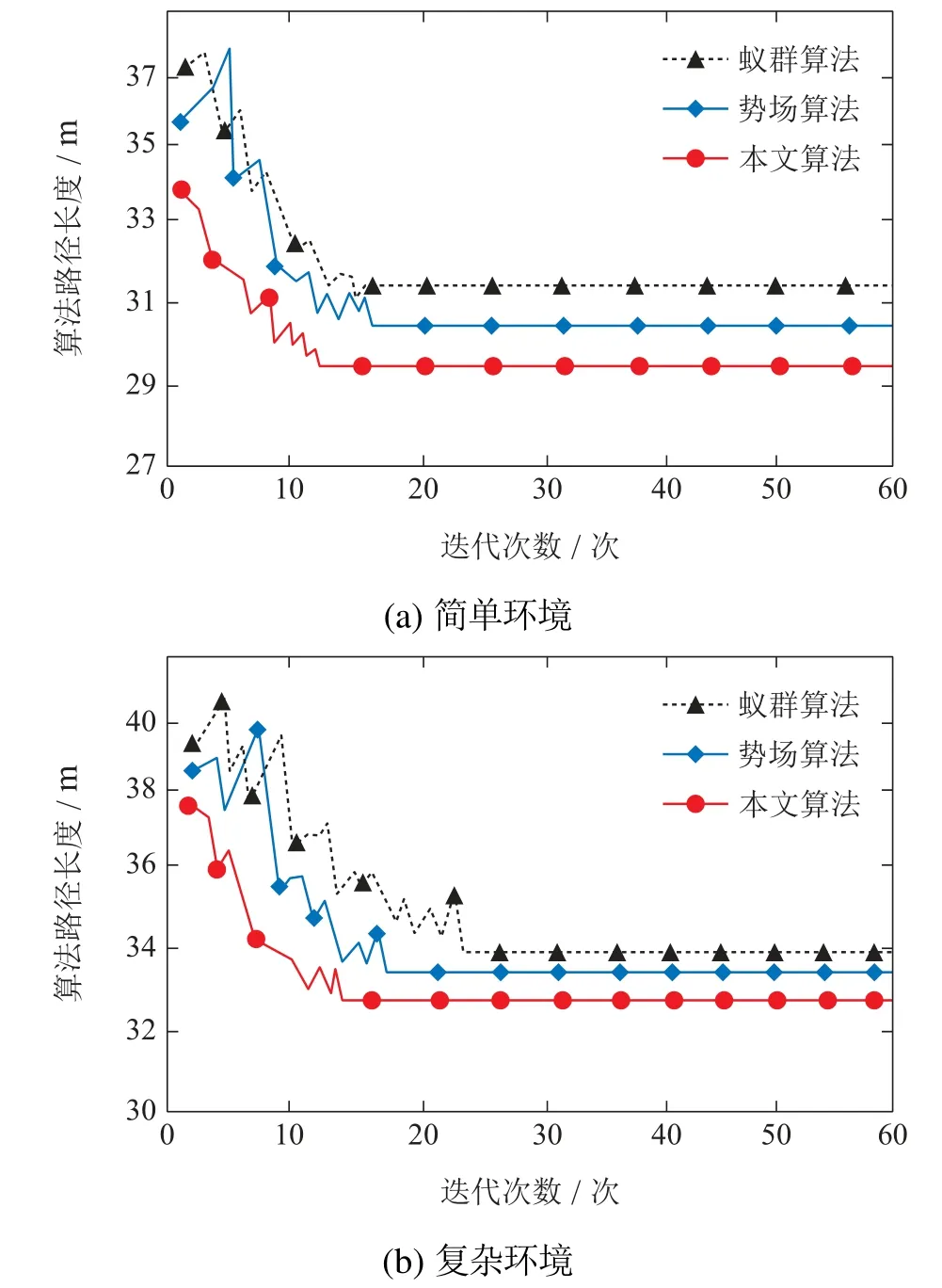
图4 不同环境下3种算法仿真比较Fig.4 Comparison of simulation in different environment
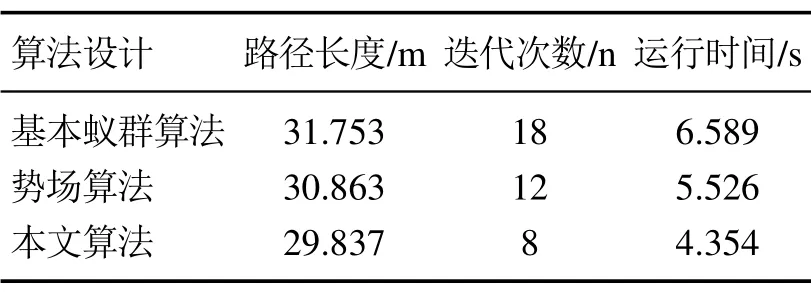
表2 简单环境下3种算法对比Table 2 Comparison in simple environment
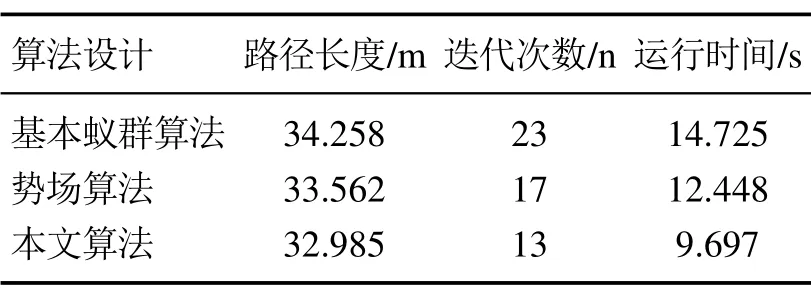
表3 较复杂环境下3种算法对比Table 3 Comparison in complex environment
3 全局路径优化
改进后的蚁群算法得到初始路径是由很多折线段构成,一条良好的路径应该有以下特点:为了船体的易操作性,应尽量避免船体频繁转向以及大幅度转向,因此,首先对得到的路径进行优化合并,去掉很多不必要的转向,方法如下:由上述算法得到的路径,对于其中的航点Mi,Mi+1,Mi+2,如果航点Mi,Mi+2的连线之间没有与障碍物相交,则把其中间的航点Mi+1去掉,直接连接两个航点;接下来循环这一算法,Mi与Mi+3之间,Mi与Mi+4之间,去掉中间航点,然后继续迭代,当Mi和后续的某一个航点的连线有障碍物相交时就中止这一迭代过程,重复这一过程,直到最后到达终点,这样得到的路径避免了很多不必要的转向,同时优化了全局路径,如图5所示,根据改进蚁群算法得到的航点依次为(S,Mi,Mi+1,Mi+2,Mi+3,Mi+4,G),经过优化后航点为(S,Mi,Mi+4,G).
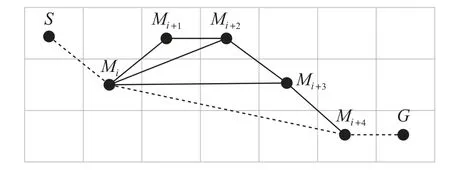
图5 全局路径航点优化Fig.5 Global path way-points optimization
4 折线段平滑曲线算法分析设计
4.1 平滑路径性能约束分析
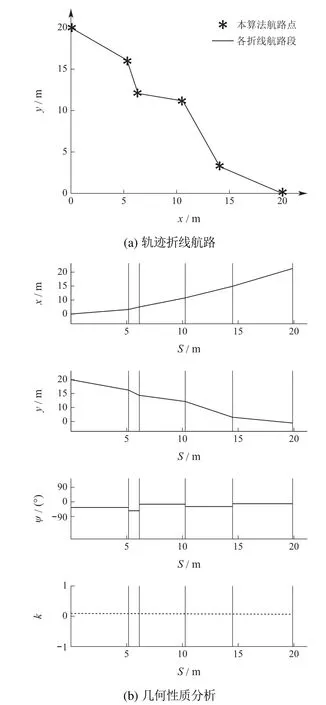
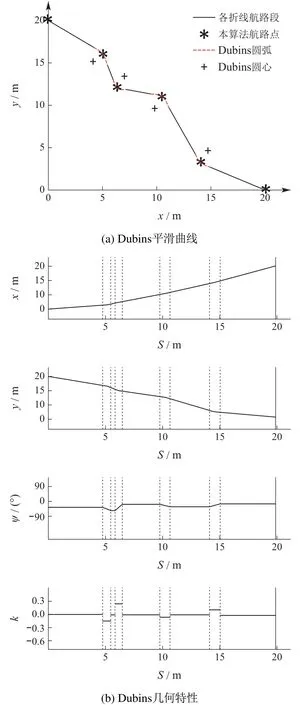
经过改进蚁群算法生成的路径以及全局路径航点优化后,其最终生成的轨迹折线航路如图6(a)所示,通过其几何性质进行分析,图6(b)所示,对于直接由航路点连接成的折线段路径,其路径方位ψ及曲率κ均不连续,不能作为USV可行路径,对于执行器的路径任务,必须受其本身机动性能的限制,在行驶至航路点时,必须满足方位及曲率的连续约束,其回旋半径约束满足如下条件:

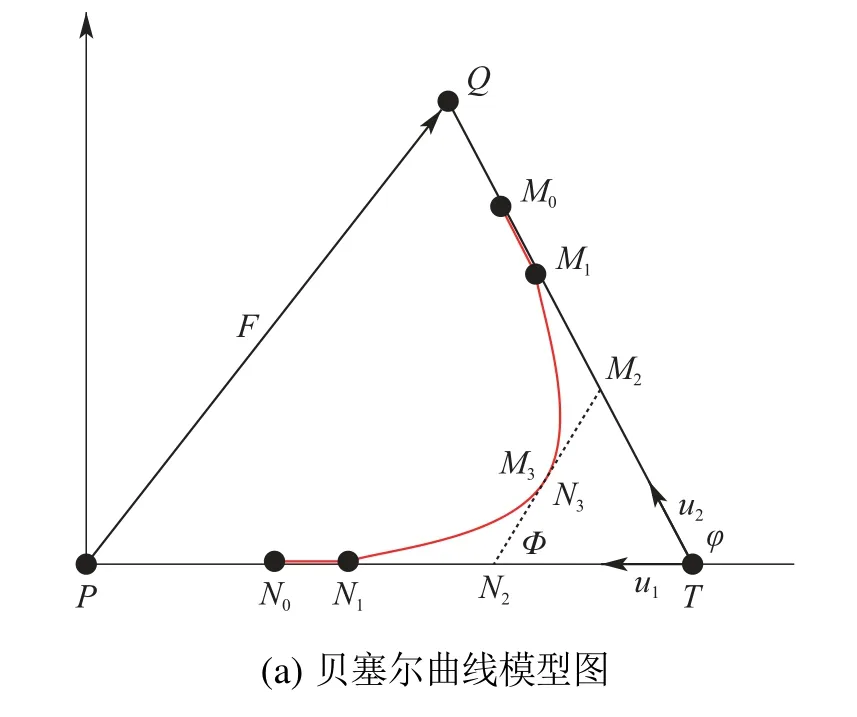
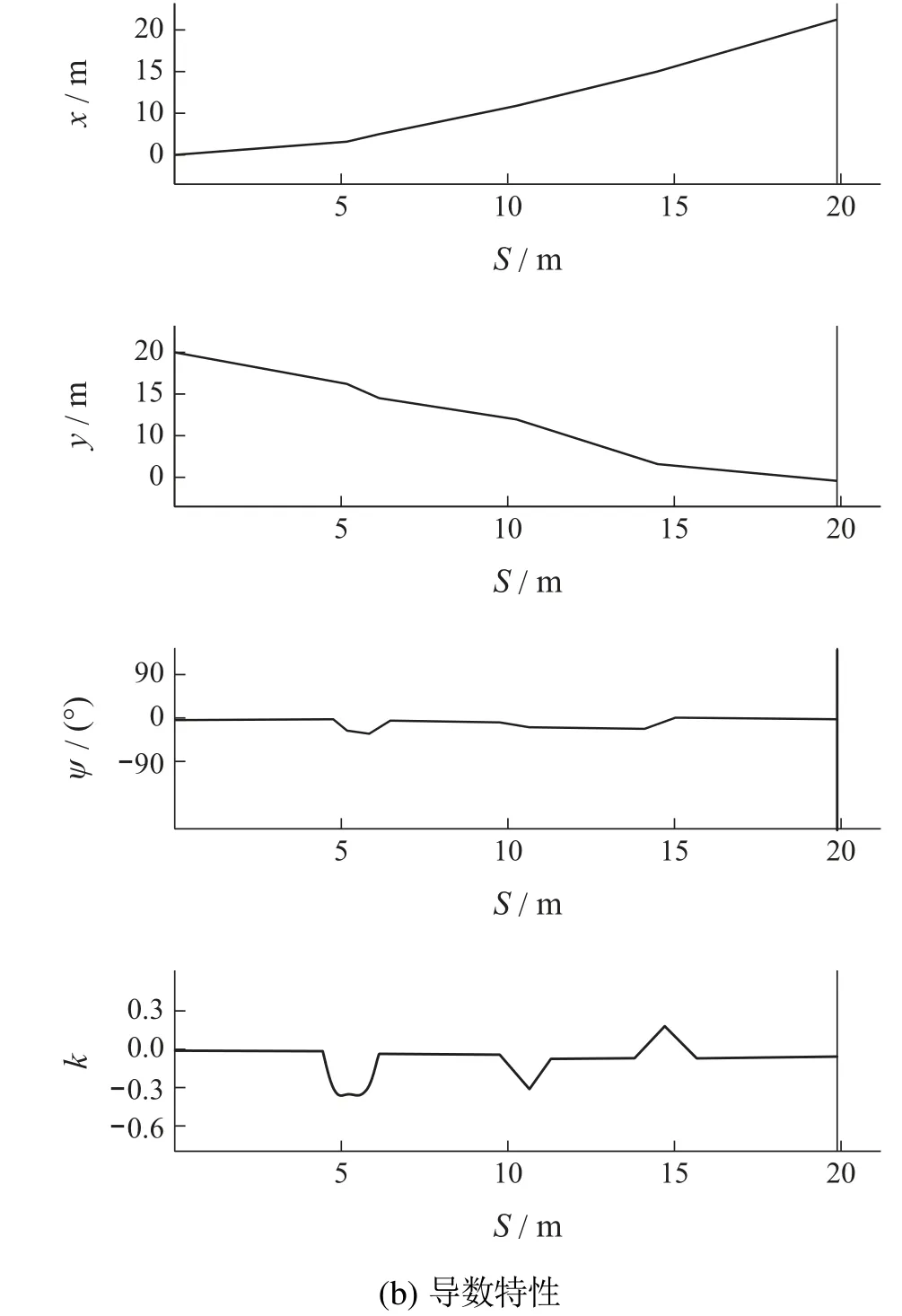
上式中:R(Rmin 首先使用Dubins路径算法对图6(a)所示路径进行平滑处理,假设在连接点处,圆弧的任意参数曲线形式表示为 图6 轨迹折线航路及其几何性质分析Fig.6 Trajectory of poly-line route and its geometric properties 式中:λ为圆弧参数;O=[a0,b0]以及R为圆弧所在圆的圆心及半径;α0和α1分别为圆弧的起始方位和终点方位,则曲线的方位和曲率分别为 经过Dubins平滑算法处理以后,在航路点处,也即各线段的连接处,用一段圆弧来代替原来的折线,如图7(a)所示,由式(9)–(10)得到的曲线方位和曲率可平滑两段直线航路段,形成一条理论可行的航线段. 图7 Dubins平滑曲线及其几何特性Fig.7 Dubins smooth curve and its geometric properties 经过Dubins平滑处理后的折线段,还并不是USV行进的最优化路线,由运动学定理可知,USV路径的曲率与航行器的横荡加速度之间[21–22]存在如下关系: 式中:µ为USV的速度矢量,α为横荡加速度矢量,曲率的不连续会造成航向控制器控制输入的不连续,对于由上述算法得到的初始路径,该折线段的二阶导数不连续,如图7(b)中的曲率几何性质κ所示,也即在连接点处曲率不连续,这会造成航行器横荡加速器的跳变,进而使得USV偏离期望航路,一条良好的路径同时应保持船舶行驶的连续性,即在保持方位偏航连续性的同时也要保持曲率连续. 为了平滑满足最小旋转半径且一阶二阶导数均存在的两条不同直线,利用贝塞尔曲线理论:对于有n+1个控制点(P0,P1,···,Pn)的n阶贝塞尔曲线,由文献[23]有如下定义: 为减少参数量,使用镜像法则,并令l=l1=l2,不失一般性,假设φ=2φ,则由图9可得 把式(17)代入式(16)可得 同时也可以简化式(15)的相关参数为 式(19),只要找到l,就能构造三次贝塞尔曲线,通常情况下,相邻两条直线的前一条直线段用于构造满足最大旋转曲率半径的圆弧,在第1段弧的最后一个点M1中,根据式(14),其三次贝塞尔曲线的一阶和二阶导数分别为 因此,其三次贝塞尔曲线的最大曲率半径为 把式(19)中的相关参数代入式(21),则可以得到 由于l≠0且φ≠180◦,则由式(22)可知κmax是一致连续的. 为了验证贝塞尔三次曲线平滑策略的有效性,首先分析其几何特性,由图8(b)可知,其偏航角和曲率在从起点到终点的过程中始终是连续的,且偏航角不存在大幅度的转向,曲率的变化曲线也不是很尖锐陡峭,不需要对动力大小及方向进行大规模的调整,这也在实时控制上满足了USV的运动学及动力学特性,同时为了验证算法的优越性,将其与文献[16]与文献[17]的算法在相同环境下进行了仿真测试,图9(a)模拟了较为复杂的USV障碍物环境,从测试结果可以看出,3种算法都能得到一条平滑可行的路径,本文由于对信息素进行了改进,同时优化了航路点,因此具有最短的航路距离以及最少的转向曲线,从USV运动学及动力学理论来分析,更短的距离及最少的转向,只需要较少的能耗,图9(b)中模拟了在较大搜索空间情况下3种算法的仿真结果,在较大空间环境中,3种算法的搜索效果差距不是很明显,但是本文中的算法还是得到了最短的路径,这是因为在初始时及整个航行过程中,USV随时与周围环境进行信息交互,其信息素随时进行更新,更能得到优化的结果,由于本文所设计的算法是从USV的自身动力航行特点和机动性能出发的,因此所规划出来的路径在能有效避开障碍物和满足可行性的同时,也实现了USV自身旋转角度和路径曲率的连续性,而且是一条优化后的路径. 图8 贝塞尔曲线模型图及其导数特性Fig.8 Bezier curve model and its derivative properties 图9 全局平滑路径对比Fig.9 Comparison of three global smooth path 针对USV的全局路径规划问题,提出了一种基于改进蚁群全局路径规划算法,得到的路径通过与其它两种算法进行对比,是一条优化后的由航路点序列顺序连接而成的安全且较短的路径,然后对其航路点进行全局优化,减少不必要的航路段,在可以减少USV油耗的同时也降低了路径长度,其时空开销得到了一定程度的降低,最后利用三次贝塞尔曲线理论平滑原来的折线段,在满足最小旋转半径的情况下,可以保证其路径上任一点的方位和曲率是连续的,仿真实验结果也验证了本文所设计的算法的有效性及优越性,USV可以生成一条光滑可行的路径,对于小型USV的路径规划及控制,具有一定的研究意义.4.2 Dubins平滑算法
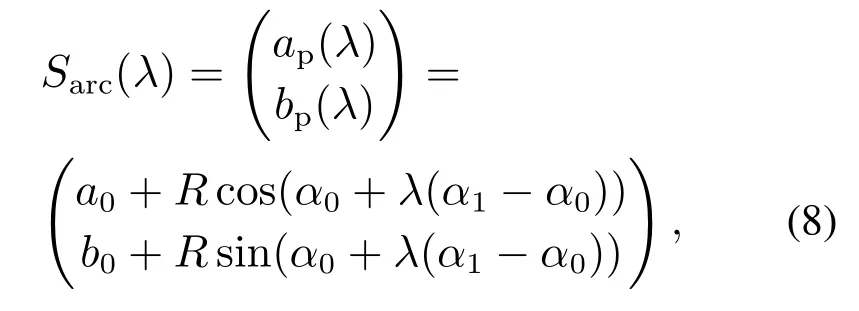


4.3 贝塞尔平滑路径设计

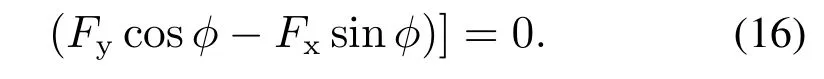
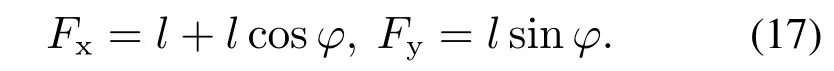
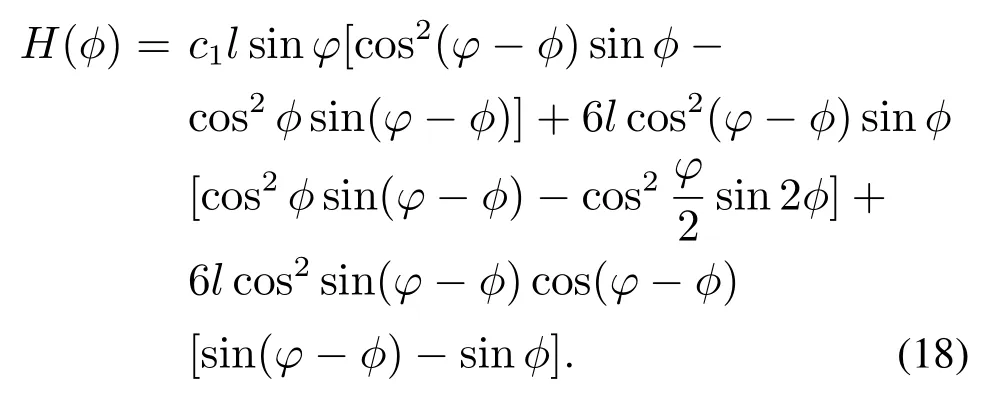
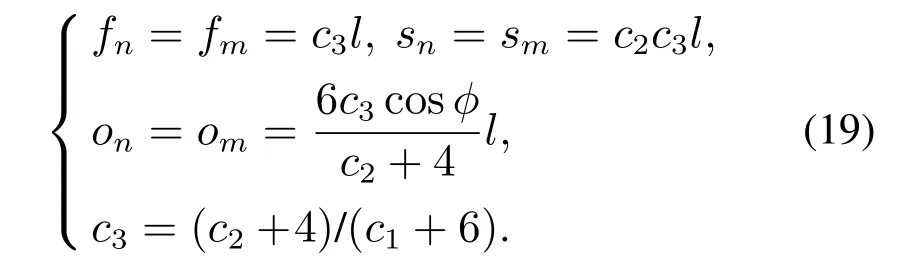

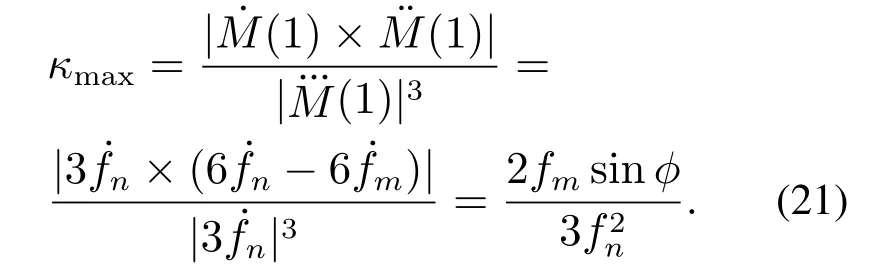
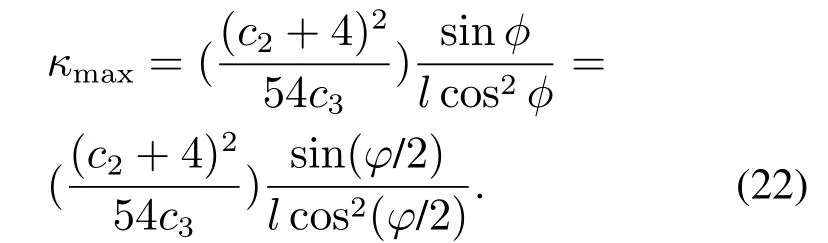
5 仿真结果与分析

6 结语

