基于分块PCA和SVM的零件识别分类系统*

李 奇，王宇钢

(辽宁工业大学 机械工程系，辽宁 锦州 121001)

0 引言

图像识别技术近年来发展越来越火热，已被广泛应用于多个领域，例如金融、医学以及人脸认证等等，给人类带来了极大的便利且在许多应用场合提高了安全防护水平。目前，许多研究者也逐渐将机器视觉技术引入到零件分类中，并获得了一定成果。

近年来，PCA-SVM图像识别算法在各大识别与分类领域得到广泛的应用创新[1]。杨宇等[2]提取了追踪目标在实时领域的相关特征，将PCA得到的主成分作为SVM的输入，实现目标追踪。许伟栋等[3]基于马铃薯形状特征，将PCA得到的前2个主成分作为SVM的输入，成功实现马铃薯自动级分选。张庶等[4]将PCA-SVM算法应用于人脸识别系统，不仅缩短了数据计算的时间，又完成了人脸识别的目标。本文将此技术应用于工厂零件识别分类中，基于其计算量和识别率两点，在经典PCA基础上，提出分块PCA算法，以提高零件图像的识别率及识别速度[5]。利用PCA算法能够有效排除特征数据间的冗余信息，而采用分块PCA可进一步提取细节特征，提升算法识别率以及运行速度；采用SVM则是基于其处理非线性数据时具有的较理想的性能。

1 基于分块PCA-SVM算法的零件识别

零件识别时通过分块PCA对图像进行特征降维，提取出主特征向量，再将其送给SVM进行训练，并运用网格搜索法优化SVM参数，然后实现零件的自动分拣。分块PCA-SVM算法具体流程如图1所示。

图1 分块PCA-SVM算法流程

1.1 PCA算法

PCA是将图像的高维数据压缩成低维数据(即无相关性的主成分向量),去除掉具有相关性的冗余信息及噪声，提取后的主成分特征要尽可能地代表原图像数据。它先是基于K-L(Karhunen-Loeve)正交变换定理，从原图中提取出少量具有代表性的互不相关的主成分向量；同时运用奇异值分解(Singular Value Decomposition, SVD)定理简化计算步骤，更快速地计算出所求的特征向量。PCA算法的特征提取步骤如下：

(1)设集合A包含M张图片，即：

A={x1,x2,…,xi,…,xM}.

(1)

其中：xi=[xi1,xi2,…,xiN]T为第i个图片灰度值矩阵的列向量，N为矩阵的维度。由此可见A是M×N阶的矩阵。

(2)求平均值图的列向量：

(2)

(3)求样本差值zi：

(3)

(4)求协方差矩阵C：

(4)

其中：Z=(z1,z2,…,zM)。

(5)求矩阵C的特征值λi和特征向量ui，并取数目为d个的特征值λj及特征向量uj，以此特征向量构成投影特征空间U：

U=(u1,u2,…,uj,…,ud).

(5)

步骤(4)中计算矩阵ZZT的维数较高，直接求其结果会影响计算速度。但依据矩阵AAT特征值与矩阵ATA特征值相同的原理，求取ZTZ的前d个非零特征值ηj及特征向量vj，再根据SVD定理获得ZZT的特征向量：

(6)

从而就可以得到步骤(5)要求的特征子空间。

一般使用的特征值选择方法是：通过计算阈值确定特征零件空间维数，保留的特征向量对应的特征值之和与原图像特征值之和的比叫做贡献率ei,计算公式如下:

(7)

其中：e为阈值。只要选择的最小值d满足式(7)即可。

图2为经典PCA算法进行降维得到的主成分特征零件。

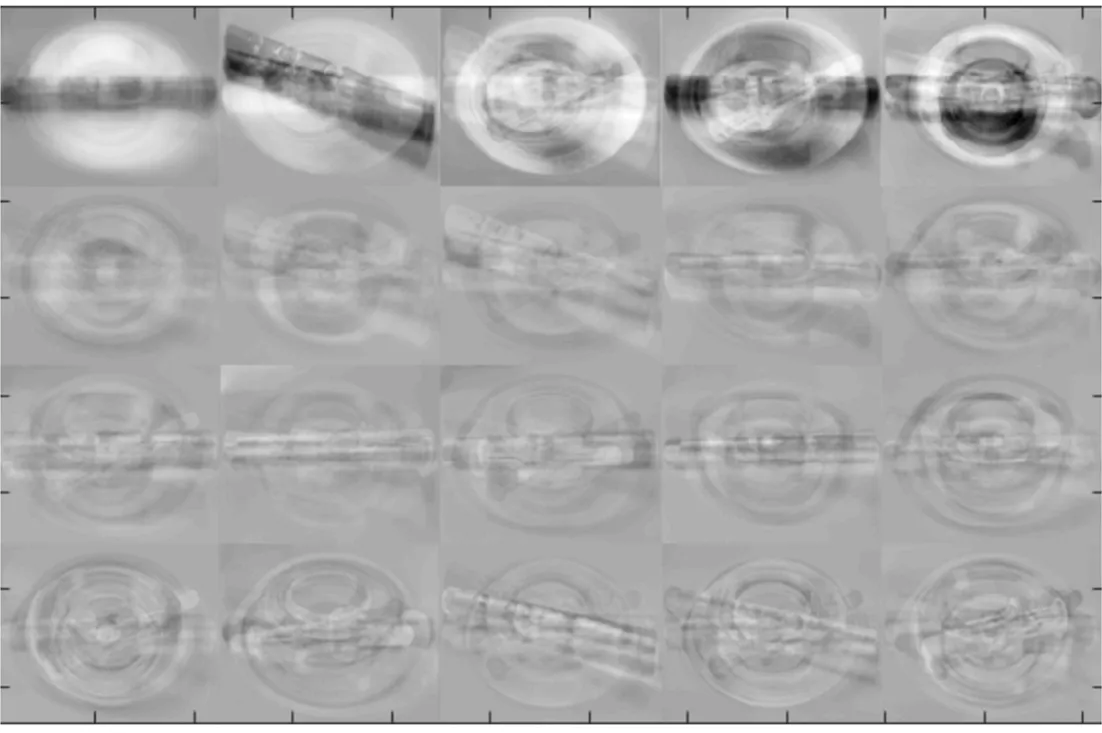
图2 PCA提取的主成分特征零件

1.2 分块PCA算法

通过对PCA算法分析，其对噪声及光照影响比较敏感，容易影响系统识别率，并且计算矩阵维数较高，不利于系统实时地自动分拣零件。本文提出基于分块PCA的零件识别改进算法。首先对图像进行分块，抽取局部特征，以减小外界环境影响，从而保证一定的识别率；然后对每一小块矩阵使用PCA算法，此时矩阵维数减小，计算量相应地减小，缩短了算法运行时间；最后再将投影后的子块矩阵合并起来。虽然处理的矩阵增多，但每个矩阵的维数大大地减小，因此最后综合计算量还是减小。分块PCA计算步骤如下：

(1)先将一张图像为m×n的矩阵B切分成p×q个子块图像矩阵，即：

(8)

设子块矩阵大小为m1×n1，其中pm1=m,qn1=n。

(9)

(2)求解所有训练样本子块矩阵的协方差矩阵S：

(10)

(3)求矩阵S的特征值λf及特征向量ωf，并依据特征值的贡献率阈值h选取前z个特征值λt及特征向量ωt使其满足式(11)：

(11)

(4)将前z个最大特征值对应的特征向量组成投影空间，再将所有训练样本的子块矩阵投影到该投影空间，获得投影矩阵Ug(g=1,2,…,pqR)。

(5)将各个Ug按照原来的标号进行合成，从左到右从上到下,即合成矩阵Ca(a=1,2,…,R)为：

(12)

图3为分块PCA算法进行降维得到的主成分特征零件。

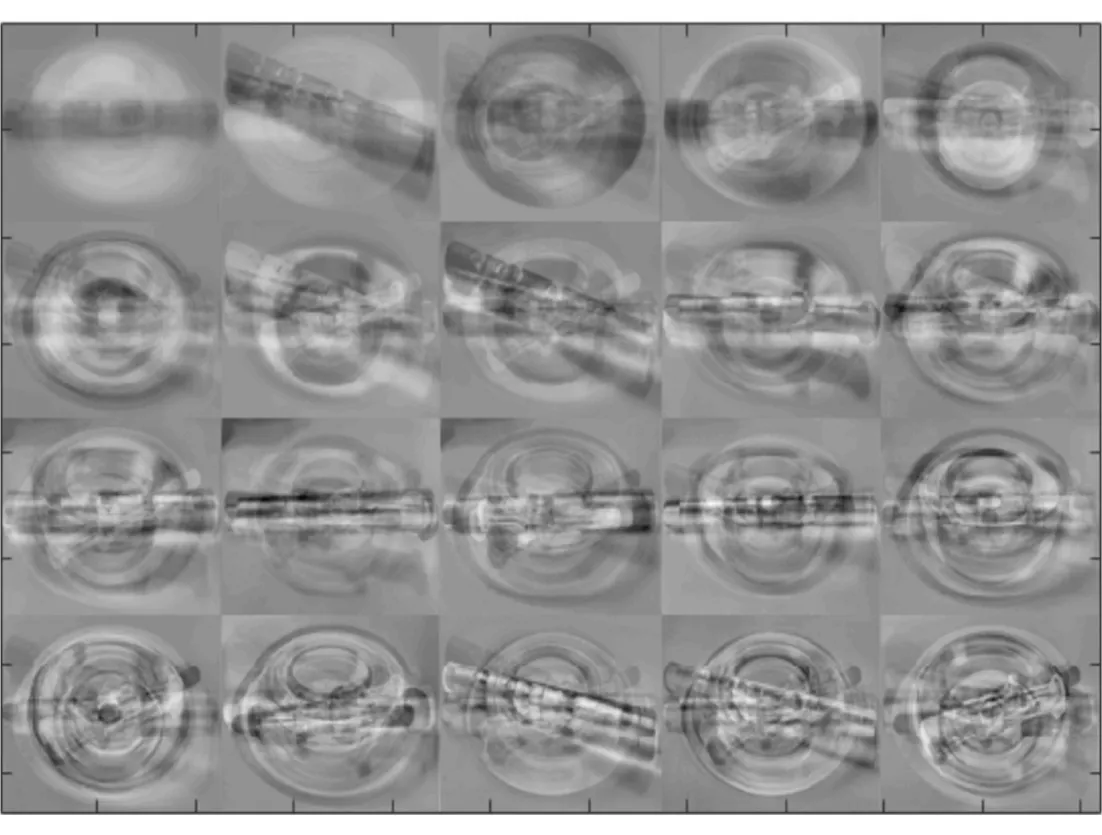
图3 分块PCA提取的主成分特征零件

比较分块PCA算法与PCA算法提取特征后得到的特征零件，由图2、图3可知，当特征维数为20时，分块PCA提取的特征零件与原始零件更相近且更清晰，其具有与原零件很高的相似度。因此，分块PCA对零件提取的主要特征更具代表性。究其原因，是由于分块PCA将一幅较大的图像分成若干个较小的图像，这样能够有效地提取图像的局部特征，所以提取后的特征零件更加清晰，且当外部环境变化比较大时，也能够保证一定的识别率。

1.3 SVM算法

SVM本质是个线性二分类器模型，在解决线性情况时，可以直接构造一个最优与最佳的分类面，而遇到非线性情况时要选择合适的核函数将低维空间样本隐式映射到高维空间中，然后在高维空间中求解最优分类超平面[6]。

本文采用的核函数为径向基函数(RBF):

K(xi,xj)=exp(-γ‖xi-xj‖2).

(13)

其中：xi和xj表示样本;γ为核函数半径。

RBF核函数参数的优化关系着SVM模型的识别率。本文运用LiBSVM工具箱中基于交叉验证及网格搜索的参数选择方法[7]。基于分块PCA-SVM算法的数据集搜索过程如图4所示。

图4 基于分块PCA-SVM的数据集搜索过程

最终获取支持向量机模型的最佳参数：c=8;γ=0.007 812 5。其中，c代表误差容限度，该值越小越容易欠拟合，越大越容易过拟合，因此c值过大或过小都会使SVM模型泛化能力变差；γ代表核函数半径，其决定数据映射到新特征空间后的分布。

本文采用“一对一的投票策略”，使SVM二分类器模型能够解决多分类样本问题。训练时，在任意两样本之间构造一个二元分类器。此时，k类样本数据将构建k(k-1)/2个SVM。测试时，计算多个分类函数，然后将测试样本归于投票最多的组。

2 实验算法的测试结果及对比分析

基于MATLAB平台设计并搭建了零件识别系统，使用50张五种零件图片作为本实验的原始数据库，其中每组的前6张作为训练集，后4张作为测试集。实验选取的五种零件数据集如图5所示。

图5 五种零件数据集

通过设计GUI界面，调控参数c与γ的值[8]。基于GUI系统验证PCA-SVM算法及分块PCA-SVM算法，操作后两种算法的零件识别率及识别效果分别如图6和图7所示。

从图6和图7可知，改进前后的算法分别识别同一数据集时，分块PCA-SVM算法的识别率比PCA-SVM算法高出10%。

图6 PCA-SVM算法识别结果

图7 分块PCA-SVM算法识别结果

用四组不同特征向量个数来对比PCA、PCA-SVM及分块PCA-SVM算法识别零件的性能，统计的测试数据如图8所示。

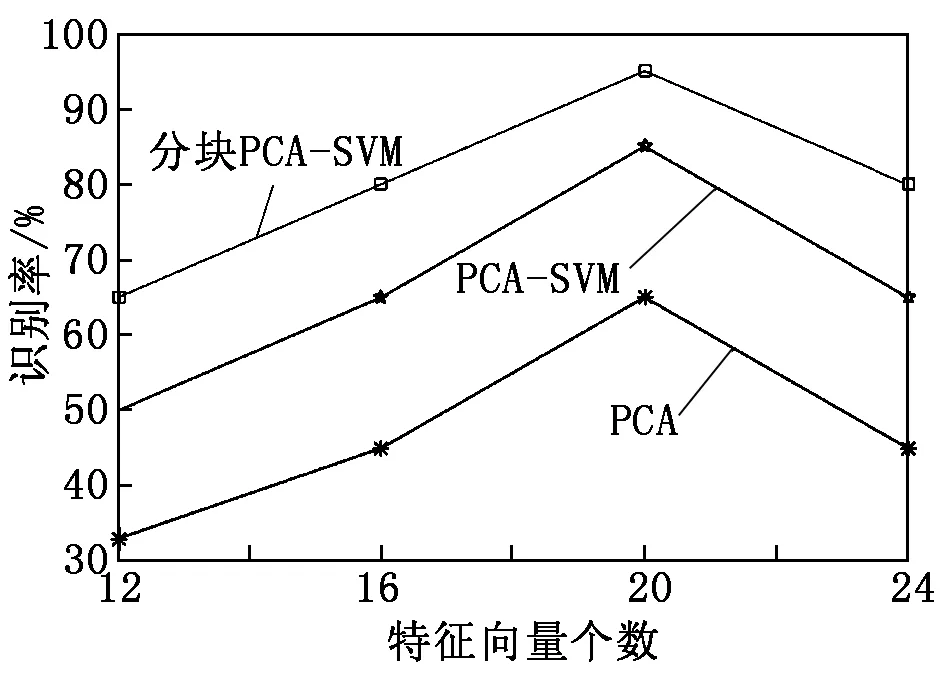
图8 三种算法识别率比较

由图8可知，提取特征向量为20时识别率最高。因此，本文算法提取特征向量设置为20。

进一步检验提出的改进算法性能，在相同实验环境下，将改进算法与经典PCA和PCA-SVM算法进行比较，识别率和算法运行时间如表1所示。

表1 三种算法零件识别性能比较

由表1可知：分块PCA-SVM算法比PCA-SVM和经典PCA算法在识别率上有所提升；同时，算法运行时间也较短。由此可见，分块PCA-SVM算法在保证一定识别率的前提下，缩短了算法运行时间，这为实际工厂作业中流水线上零件分类的实时性带来了很大保障。

3 结论

本文设计的分块PCA与SVM算法相结合的零件识别分类系统，主要实现了工厂零件的自动化分拣。当工厂噪声及光照环境影响较大时，分块PCA算法能够有效地抽取图像局部特征，进而提高识别率及运行速度。最后比较了不同维数下各算法的识别性能，本文提出的分块PCA-SVM算法，基于特征向量个数20，识别率达95%，运行时间0.4 s。

实验结果表明，本文提出的方法应用于零件自动化分拣是可行的，为将机器视觉识别应用在工业生产中奠定了一定的基础。