智能车跷跷板运动行进平衡算法的研究与实现*

杜金祥，岳 光

(太原工业学院 自动化系，山西 太原 030008)

0 引言

鉴于很难确定智能小车精确的数学模型以及无法确定的外界干扰，特别是行进跷跷板的平衡，利用传统的控制理论很难实现对智能小车的高精度平衡控制[1]。基于目前国内传统电动车跷跷板控制系统的已有算法，经过多次的实验测试和算法分析，本文提出了一种新颖的基于神经网络BPTT电动车跷跷板运动控制方法。其采用专门应用于控制领域的STM32F103C8T6芯片为控制系统核心，采用随时间反向传播(Backpropagation Through Time,BPTT)算法PID控制技术[2]，通过陀螺仪传感器MPU6050精确测量电动车的运行姿态数据，精确控制驱动四个电机的运转速度，达到对电动车跷跷板运动的精确控制，在完成指定任务后报警模块给予任务完成提示，同时STM32F103C8T6芯片外扩LED显示屏，方便用户读取数据。该设计主要是针对小朋友的智能电动玩具以及一些模拟比赛进行的研究，具有一定的参考价值和实用意义。

1 智能车跷跷板运动控制系统

图1为智能车跷跷板控制系统结构框图，它由STM32F103C8T6为核心的主控制器组成的主控系统、小车速度控制子系统、小车角度检测子系统和运动执行机构组成。智能车角度检测子系统的主要功能是实时检测小车运行角度，并计算出角度偏差量；速度控制子系统基于先进的神经网络BPTT与深度学习PID控制算法,通过三维角速度陀螺仪加速度计模块MPU6050对跷跷板三维运动状态的数字信号进行采集、计算[3],得出相应的值,输出到直流电机控制回路参与跷跷板姿态控制。

图1 智能车跷跷板控制系统结构框图

2 智能车跷跷板运动原理及控制策略

智能车跷跷板运动原理如图2所示，跷跷板处于两边都悬空的状态，小车在起点端安置配重(质量为m1),当小车(质量为m2)从一边行驶上跷跷板，越过支点C,板的一端开始受力直到车体到达板的平衡重力点位置，跷跷板两端受力均匀，此时达到平衡。本次设计实验中的跷跷板选择长度160 cm、宽度30 cm的轻质PVC板，m1和m2的质量远远大于PVC板质量，所以建模时忽略板的质量。控制系统的工作原理是：智能车驶上跷跷板后，通过倾角传感器不断地测量跷跷板的倾角(即实际倾角)，该实际倾角与给定倾角作比较，形成倾角偏差，通过电机控制智能车前后微移，不断修正该倾角偏差，最终使倾角保持在给定范围之内，此时跷跷板便达到平衡状态。

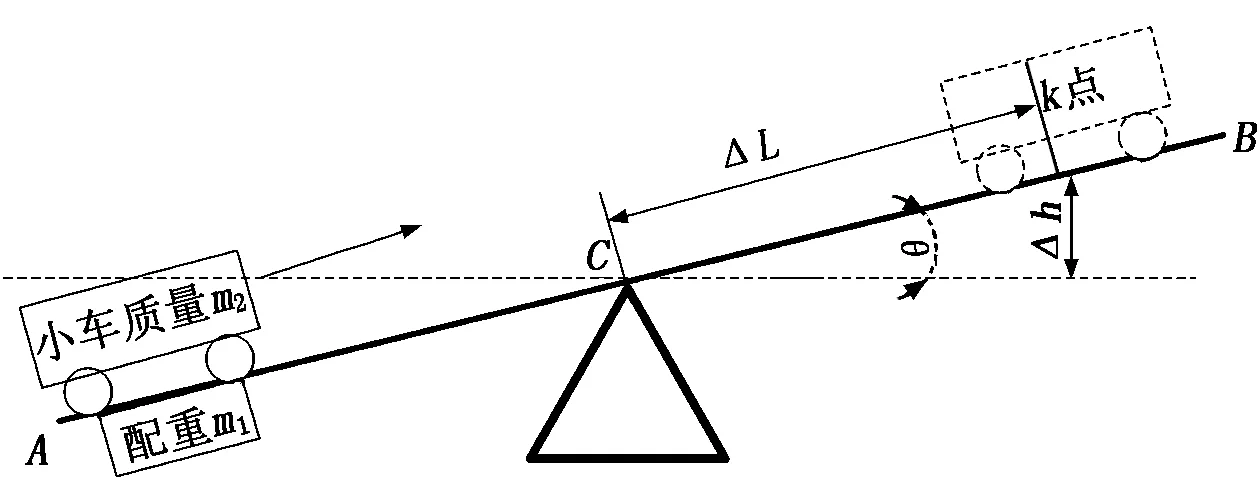
图2 智能车跷跷板运动原理

要使智能车跷跷板运行具有一定的稳定性及精确度，我们需要通过MPU6050传回的姿态数据实时提供跷跷板的倾角θ，依据θ在运行时间内的变化，可以计算出系统相关参数。图2中，Δh为跷跷板在任意点k的高度，ΔL为过支点后任意点k的小车位移距离。在运动控制平衡的任务中，开始运动只提供跷跷板的倾角θ，通过倾角θ来控制电动车运动速度。再设置规定倾角为目标角度，其与实际倾角的差值为偏差,联系跷跷板变量倾角θ与运动速度u得出在k点时刻有下式成立：

θ=arcsin(Δh/ΔL)=arcsin(Δh/ukt).

(1)

AB杠杆以C为圆心转动，根据扭矩平衡∑M=0，又考虑到过C点后小车做减速运动，经过多次测试取初速度u0=0.312 m/s。设在任意点k的加速度为a(k)，由位移距离ΔL得方程：

(2)

由角速度陀螺仪测得的数据可计算角加速度α(k)，再将其转化为加速度，用公式表示为：

a(k)=ΔLα(k).

(3)

依据杠杆原理扭矩总和∑M=0,在任意点k处得出:

m1×|AC|-m2×ΔL=0.

(4)

这样依据公式(1)～公式(3)建立受控对象的差分方程:

y(k)=0.312y(k-1)+0.26y(k-2)+

0.11u(k-1)+0.312u(k-2).

(5)

其中：y(k)为控制对象在k时刻的输出值。

本系统中通过智能车在跷跷板上的运动,动态地调整跷跷板的角度,使电动小车的重心恰好处在跷跷板的平衡点。针对平衡系统的主要任务是设计小车，即对系统搭建实际平衡车模型，然后再集中对小车进行设计。

3 跷跷板控制系统控制流程及BPTT PID算法设计

跷跷板小车控制系统根据角度偏差调整速度反馈值，在CPU的PID控制器采用了基于BPTT神经网络的PID控制构架，如图3所示，其组成部分为BPTT神经网络运算器(图3 中虚线框内部分)和PID控制器(u(k)与Δu(k)反馈及受控对象部分)，这种组合控制策略能够利用PID和BPTT神经网络的最优功能[4]，结合以STM32F103C8T6为核心的主控制器开发的硬件平台，使控制参数达到最优。

图3中，转换器的功能是进行微积分计算，其输入为设定值r(k)与输出值y(k)的误差e(k)=r(k)-y(k)，Δu(k)为控制率信号u(k)与控制器输出量加一步延迟后的误差值。转换器的输出为神经元学习控制所需要的输入状态量x1、x2、x3，分别取：

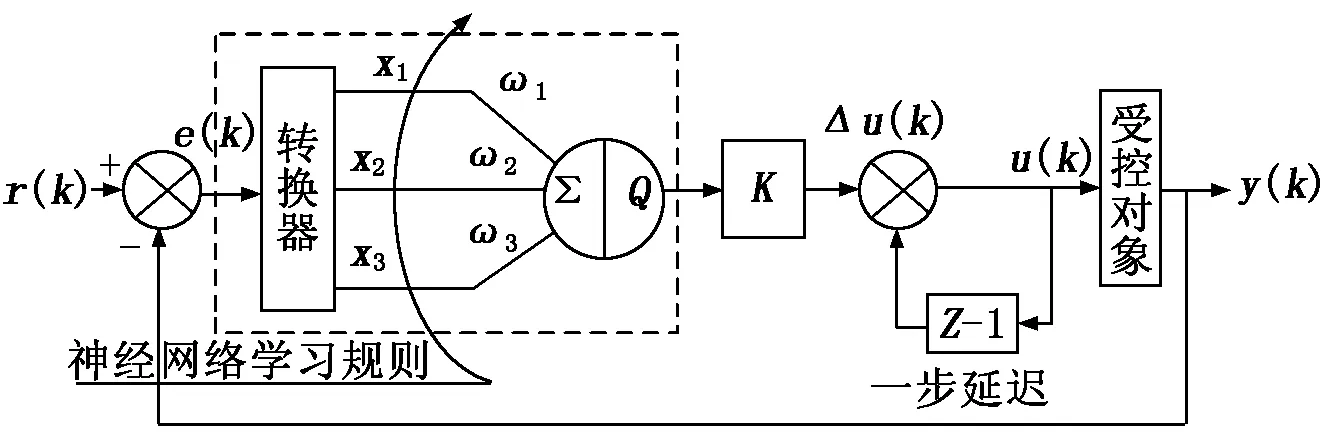
图3 深度学习PID控制结构图

(6)

设ω1、ω2、ω3为神经元各输入状态量所对应的权系数，神经网络的阀值Q取为零，使用改进的Hebb学习算法得到三个权值的更新规则为：

(7)

其中：ηp、ηi、ηd分别为比例、积分、微分的学习速率。可以选择这3个权值变量为系统的状态变量。

神经网络输出激发函数取Tanh函数，表示为：

(8)

因此，神经网络控制器的输出控制量为：

u(k)=u(k-1)+Δu(k)=

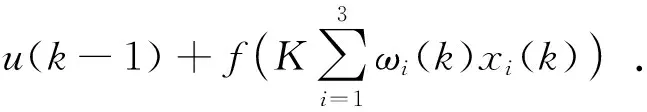
(9)

其中：K为比例系数。

神经网络的自适应功能是通过改变权系数ωi来实现的，学习规则即是如何调整ωi的规则，它是神经元控制器的核心。在这里学习算法借用最优控制中二次型性能指标的思想，在权重值的调整引入二次性能指标，实现对输出误差的约束控制。

目标函数为：

(10)

为了保证权重值修正以J(k)相应于ωi(k)的负梯度方向进行，必须满足：

(11)

其中：ηi为学习速率，1>ηi>0。学习速率η的选择也要合理恰当。本设计单神经网络自适应算法的稳定条件是：

0<η<2(AAT)-1.

(12)

(13)

学习速率决定每次循环训练生成的权值变化量。学习速率过大可提高训练效率，但可能会导致系统不稳定；学习速率过小则可能导致训练时间过长，收敛慢[5]。因此选取较小的学习速率可以保证系统的稳定性。学习速率的选取范围一般在0.001～1 之间。在本系统中为了保证系统有足够的稳定性，选择偏小的学习速率，取η在0.05左右。加权系数取值范围[-1,+1],K值取1，这样由式(10)～式(13)可得到PID的参数应满足：

(14)

Kω2(k)=Kp.

(15)

(16)

其中：T为采样周期。

这样就可以推出自适应的比例、积分、微分参数。

4 实验数据测试及结论分析

利用设计的智能车跷跷板控制系统(实物如图4所示)，测量每次跷跷板的高度变化差Δh,用秒表记录每次到达平衡所用时间，重复测试多次，并记录相关数据。同时与传统的控制算法进行比较，结果表明：与传统控制算法运行数据比较，采用BPTT的PID控制算法在平衡时间方面效率平均提高了11%，平衡高度差Δh的精度提高了29.3%。这主要是因为神经网络BPTT控制算法实时修正系统控制参数，使得反复校正次数减少，较大缩短了有效运行时间。实验数据证明了本控制算法的可行性。两种行进算法实验数据对比如表1所示。

图4 智能平衡小车控制实验

根据表1所示数据可得智能平衡小车基本能够按照预期的要求行驶在跷跷板上并将其调平衡。通过观察比较数据可以看出智能车在平衡运动方面存在着的误差Δh经过算法修正后大大减小，从而使平衡角度θ较小，达到理想期望状态。

表1 两种算法实验数据对比

5 结语

本文设计的跷跷板控制系统与传统跷跷板控制系统相比，控制核心是电机的转速，控制精确并且扩展性优越，同时采用三维加速度陀螺仪模块作为检测反馈系统部件，在输出驱动模块也采用了典型的电机驱动模块，加上神经网络BPTT的PID控制算法，从而为智能小车精确控制打下扎实的基础，同时也为下一步研究奠定了基础。