基于超单元法的不锈钢车体侧墙焊点优化

孙业琛， 孙丽萍， 王玉艳

(大连交通大学，辽宁 大连 116028)

0 前言

不锈钢材料力学性能优异、易于加工成型且耐腐蚀性能良好，被越来越广泛地应用于轨道车辆的车体上，不锈钢车体也因全寿命周期成本低而逐渐成为新型轨道车辆的主流选择。但轨道车辆专用的奥氏体不锈钢SUS301L热传导系数较低，仅为钢的三分之一，且热膨胀系数较高，约为钢的1.5倍[1]，若采用电弧满焊连接各构件，产生的热量分散缓慢，聚集的热量会引起构件变形，所以不锈钢车体构件间的连接更多地选择电阻点焊。焊点的数量与布局对不锈钢点焊车的性能及生产成本有着至关重要的影响。

目前，不锈钢车体焊点的研究主要集中在局部结构，对车体整个侧墙焊点布局的优化研究较少。杜健等人[2]对地铁不锈钢车体侧墙焊点的剪力分布进行探索，优化了最外端的局部焊点，使得焊点数量减少且布局更加合理，生产效率提高，焊点的疲劳性能也得到了极大改善。谢素明等人[3]对不锈钢点焊车的车体结构进行稳定性分析，基于子结构技术对局部焊点进行拓扑优化，使得局部失稳部位刚度提升，整个车体结构稳定性满足规范要求。

文中以某出口不锈钢点焊车为研究对象，建立有限元模型，并依据EN 12663标准，对车体进行静强度分析。在保证强度、刚度的前提下，基于超单元法和变密度法对侧墙焊点进行改进优化。

1 不锈钢车体有限元分析

1.1 有限元模型

该不锈钢点焊车是薄壁筒型的整体承载式结构，由底架、侧墙、端墙、车顶和司机室构成，通过20 000个焊点将5大部件连接起来并传递载荷。其中，整车近一半的焊点用于侧墙的构件之间的连接。整车除去牵引梁、枕梁及动力包吊挂梁等关键受力部位采用高强度耐候钢外，其余结构均采用SUS301L不锈钢。

根据几何模型，在有限元仿真软件中建立该车体有限元模型，利用20 mm的壳单元对结构进行离散，整体上采用高精度的四边形单元，部分区域通过三角形单元过渡；牵引梁及抬车座等关键受力部位采用实体单元；螺栓采用刚性单元和梁单元组合模拟；点焊采用CWELD单元，塞焊及部分断焊采用RBE2单元刚性连接。最终有限元模型共包含1 274 451个单元及1 203 627个节点。

1.2 计算工况

根据BS EN 12663-1:2010《铁路应用—铁道车辆车体的结构要求》[4]及相关技术条件的要求，确定该不锈钢点焊车的载荷、约束及评价标准。最终，建立超员、最大垂载、拉伸、压缩、抬车、三点支撑、复轨等共计12个工况。以其中最为恶劣的超载压缩工况为例，对载荷和约束的施加及有限元分析进行说明。

在此工况下，施加纵向压缩载荷800 kN，分别施加在两端车钩座中心；施加垂向载荷500.73 kN，包括车身质量26 699.5 kg、2个客室空调质量共1 400 kg、动力包质量4 630 kg、燃油箱(含2/3箱燃油)质量3 193.3 kg和载客质量15 120 kg，其中，各设备重量以集中力的形式施加在设备质心处，载客重量以均布力的形式施加在底架地板上表面；在空气弹簧处施加垂向约束。具体有限元模型及示例工况的载荷和约束如图1所示。

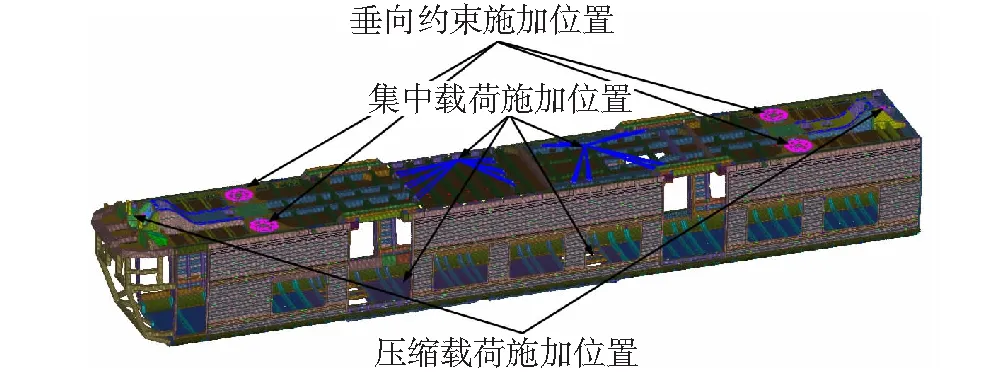
图1 车体有限元模型

1.3 静强度分析

对有限元模型进行计算求解，该工况下车体各结构的最大应力值和出现位置以及材料的屈服强度分别见表1。由表1数据可知，车体各结构的最大Von Mises应力值均小于对应材料的屈服强度，且安全系数大于标准中规定的1.15，故该车体在超载压缩工况下满足强度要求。由计算结果可知，其余11个工况各结构最大应力值同样小于对应材料的屈服强度，满足标准中的强度要求。根据GB/T 7928—2003《地铁车辆通用技术条件》要求，在最大垂向载荷作用下，车体的挠跨比应小于1‰。该车体在最大垂载工况下，底架边梁中部的最大垂向位移为9.1 mm，而该车两转向架中心间距为12 600 mm，挠跨比小于1‰，故该车同样满足刚度要求。

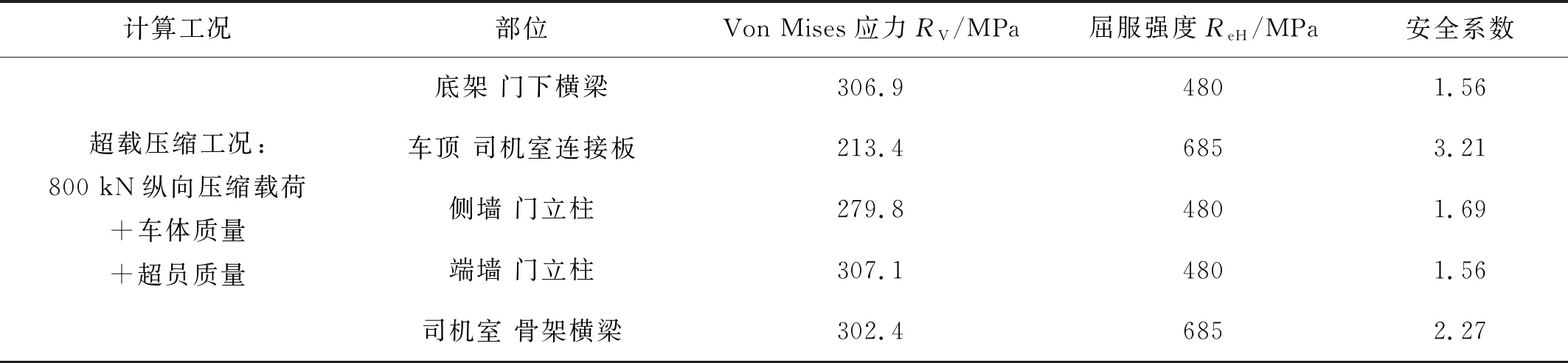
表1 超载压缩工况下车体各大部件最大应力值

2 变密度法和超单元法原理

2.1 变密度法

变密度法由均匀化方法发展而来，其设计变量为有限元模型中每个单元的“单元密度”[5]，用D表示。“单元密度”D与材料本身的密度和弹性模量相关，且0≤D≤1，当D越接近1时，表明此处的材料对目标函数的影响越大，应予以保留；相反，当D越接近0时，表明此处的材料对目标函数影响越小，可适当去除，以提高材料的利用率，从而达到轻量化设计的目的。变密度法主要有2种模型，分别是各向同性材料惩罚模型(Solid isotropic material with penalization, SIMP)和有理近似模型(Rational approximation of material properties, RAMP)，文中采用的是SIMP模型[6-7]，其数学表达式为：

(1)

式中：Ei表示第i个单元的弹性模量；E0为材料相对密度为1(即该单元充满材料)时单元的弹性模量；p为惩罚因子，惩罚因子越大越能抑制中间密度单元，但过大的惩罚因子会造成棋盘格现象，为得到传力路径清晰的优化结果，通常取p>1即可。

2.2 超单元法

超单元法是一种以有限元法为基础的高级分析方法，在研究大型有限元问题的局部力学特性时，能节省大量计算时间，并具有一定的保密作用[8]。超单元法的本质是通过适当的数学变换，在保证求解精度的前提下，将复杂结构的庞大自由度用适当的矩阵代替，然后将该变换矩阵带入所求解的局部问题自由度里，从而达到缩减求解规模、提高计算效率的目的。

缩聚的基本原理是首先将超单元分为内部结构和外部结构，所要凝聚部分的自由度称为内部自由度Xi，超单元边界的自由度称为外部自由度Xb，相应的位移即可表示为：

(2)

总刚度矩阵同样以内部自由度和外部自由度划分，则线弹性结构的静力学方程可表示为：

(3)

将静力学方程展开为：

KbbXb+KbiXi=Fb

(4)

KibXb+KiiXi=Fi

(5)

由式(5)可得：

(6)

总刚度将(6)代入(4)可得：

(7)

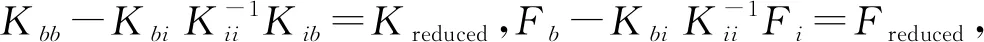
KreducedXb=Freduced

(8)

式中：Kreduced和Freduced分别代表凝聚后超单元的刚度矩阵和载荷。这样就实现了外部结构自由度的凝聚，从而可以缩减求解规模。

3 侧墙焊点拓扑优化

3.1 侧墙简介及优化流程

侧墙与底架、车顶、端墙和司机室均有连接关系，是车体结构中唯一与其他大部件全部连接的部件。该不锈钢点焊车的侧墙采用板梁式平面承载结构，主要由矩形门立柱、帽型立柱、乙型立柱、连接板等垂直构件，上边梁、窗纵梁、帽型纵梁等水平构件及上下墙板构成，具体几何结构如图2所示。

图2 侧墙几何结构

侧墙构件大多采用点焊方式连接，全车近一半的焊点密布于侧墙板与梁柱之间。而根据前述计算结果可知，在最恶劣的超载压缩工况下，侧墙最大的Von Mises应力值仍远小于屈服极限，且最大应力值均出现在门角或窗角处，板梁之间如此大数量的焊点，对车体的静强度并无显著影响，反而影响实际生产效率，故可对焊点的数量和布局进行优化，消除冗余焊点。优化流程如图3所示。

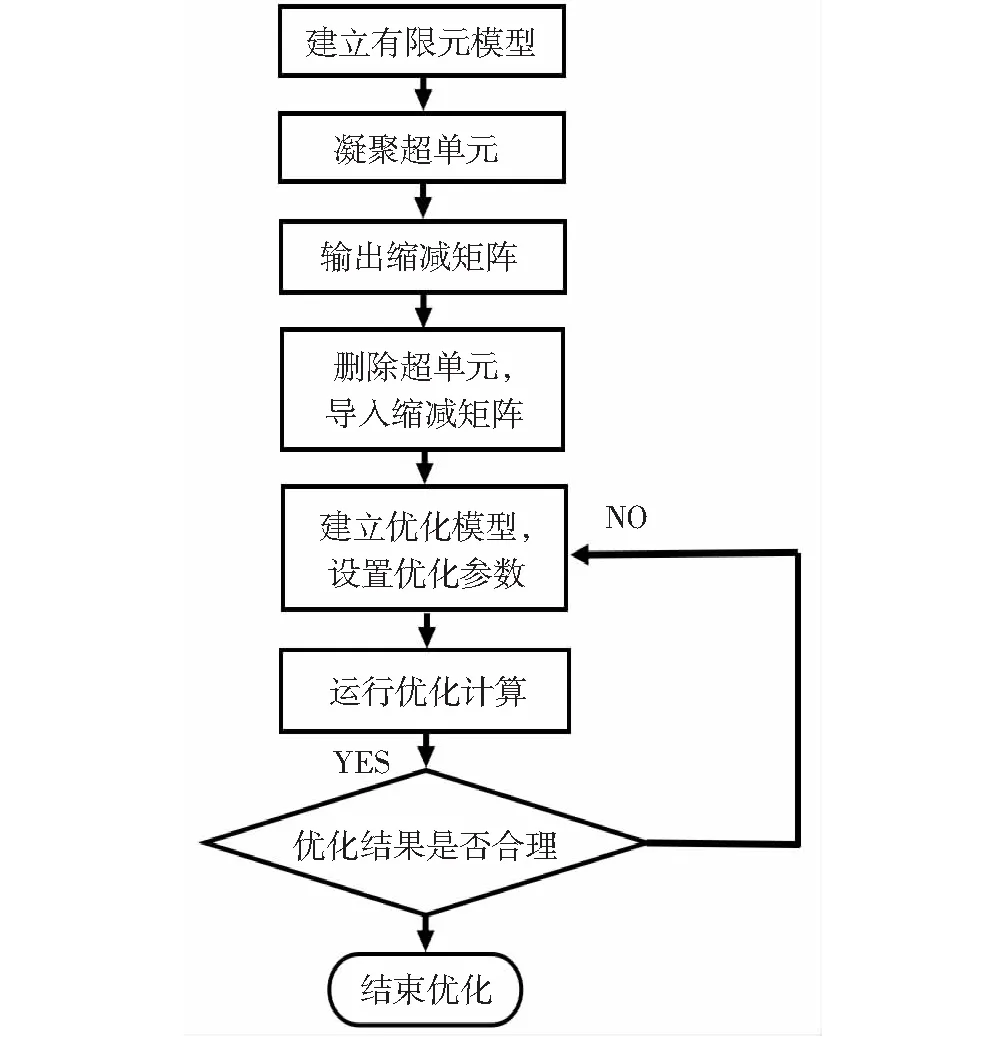
图3 优化流程图

3.2 优化模型

考虑焊点在组合载荷下的不同受力情况，保证优化结果在所有工况下均能满足相应要求，且充分考虑计算求解时间及不同工况对优化结果的影响程度，综合选择在最大垂载、超载拉伸和超载压缩3个较为恶劣的工况下进行优化。优化设计的数学模型描述为：①目标函数：规定工况下加权柔度最小；②设计变量：侧墙中所有直径7 mm的焊点单元；③约束条件：设计变量中所有焊点单元的体积分数，为更加清晰对比得出重要焊点的分布情况，逐次将优化后单元的体积分数设置为占原体积分数的80%～90%，70%～80%，60%～70%，50%～60%。

由于该车体的几何结构和载荷约束均关于纵向面对称，可只选择一侧侧墙的焊点作为设计变量，将底架、车顶、端墙、司机室及另一侧侧墙凝聚成超单元，进一步提高优化效率。若对整车模型进行优化，共1 274 451个单元，使用24核48线程、128G运存的工作站计算，单次优化耗费机时80 min左右；而使用超单元缩减后的模型，仅225 533个单元，同等硬件条件下，单次优化耗费机时仅45 min左右，每次优化过程节省近一半时间。考虑到为使优化更加充分，计算能更收敛于最优结果，需要对优化参数进行反复组合调试，超单元法无疑能使整个优化过程的计算时间大大减少，计算效率显著提升。最终将收敛容差设置为10-5，1D单元的离散度设置为20，最大迭代步数设置为30。

3.3 优化结果分析及改进

不同约束条件下的优化过程迭代曲线如图4所示。不同约束条件下，不同单元密度所包含的焊点数量见表2。单元密度在0～0.1之间的焊点位置分布情况如图5所示。

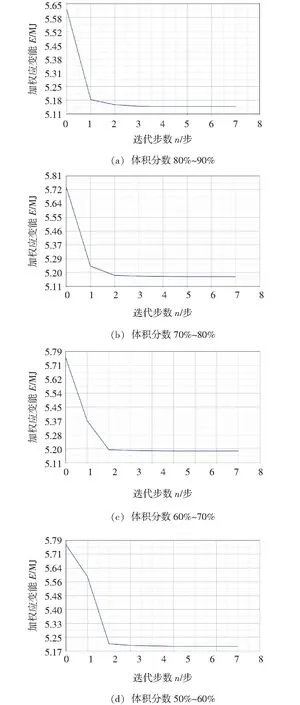
图4 不同约束条件下的优化迭代曲线

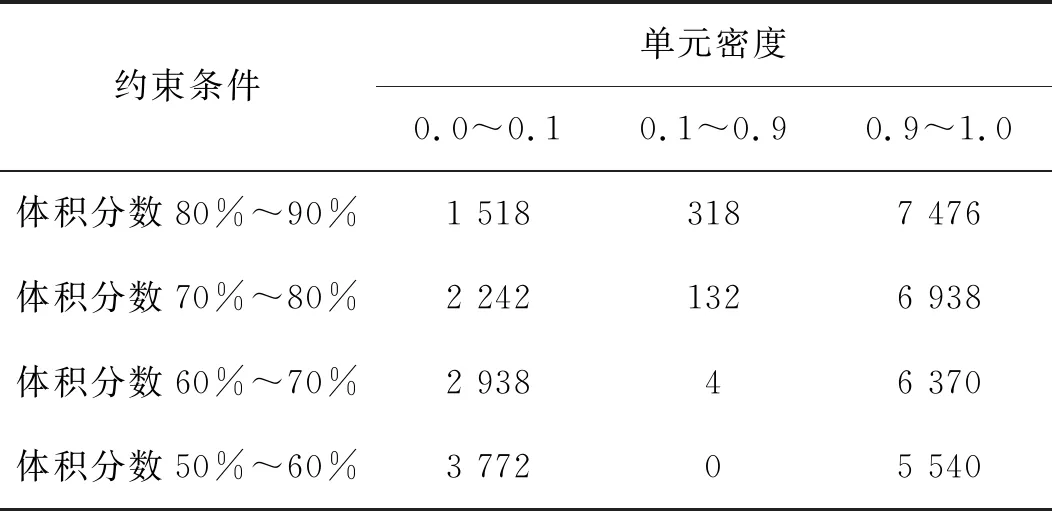
表2 优化后焊点分布表

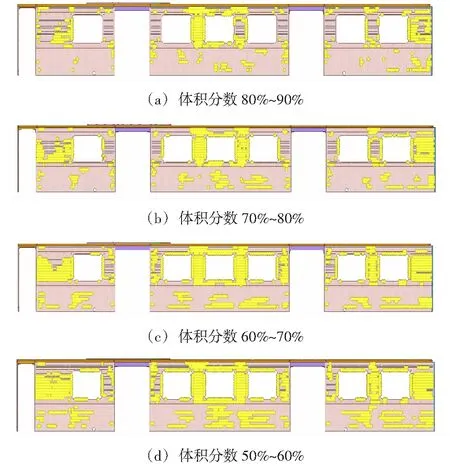
图5 不同约束条件下的焊点分布情况

由不同单元密度所包含的单元数量及优化迭代曲线可知，优化过程收敛，且焊点离散程度高，中间密度焊点数量少，优化结果可取。又由单元密度在0.0～0.1之间的焊点数量可知，该不锈钢点焊车的侧墙确实存在大量冗余焊点，冗余焊点大多集中在侧墙上墙板与帽型纵梁连接的位置，而下墙板与乙型纵梁、门立柱等构件焊接的焊点大多为传力的重要位置。综合考虑外形美观、保证各构件间的连接关系及BS EN 15085-3:2007《铁路应用—铁道车辆及其部件的焊接》中对焊点间距的要求等因素[9-10]，对优化结果加以人工改进：①将上墙板与帽型纵梁之间的焊点间距由60 mm增大至120 mm；②将上下墙板与门立柱、乙型立柱之间的焊点间距由90 mm减小至60 mm。经优化改进，侧墙焊点共减少977个，占原焊点数量的10.5%。

3.4 优化结果校核

对优化改进后的整车模型进行校核。仍以超载压缩工况为例进行说明，优化前后结果对比见表3。各构件应力变化较小，且仍低于屈服强度，满足强度要求。优化后车体的底架边梁中部在最大垂载工况下的最大垂向位移为9.2 mm，增加0.1 mm，但仍满足刚度要求。其他工况下构件的应力与位移同样变化较小，说明优化后车体的力学性能满足标准及相关技术条件要求。

表3 优化后超载压缩工况下车体各结构应力值

4 结论

(1)对该不锈钢点焊车进行有限元分析，计算结果表明该车体的强度、刚度满足标准及相关技术条件的要求。通过优化分析可知，侧墙中存在大量冗余焊点，这些焊点对车体性能影响较小，但增加了焊接工作量，影响实际生产效益。

(2)基于超单元法对局部结构进行分析，可在保证精度的前提下节省大量计算时间，尤其对于反复迭代的优化过程，计算效率可更加显著地提高。

(3)通过对侧墙直径为7 mm的焊点进行拓扑优化，在保证强度、刚度的条件下共去除977个冗余焊点，占设计变量的10.5%，优化效果明显，为设计人员在焊点的布局设计方面提供有益参考。