手套箱开启过程的动力学分析及性能设计
陶靓
(泛亚汽车技术中心有限公司,上海 201206)
1 前言
在汽车内饰件中,手套箱是消费者经常使用和关注的零件,并且随着汽车内饰的发展,消费者对于开箱过程的要求也相应提高。为响应这一需求,大部分汽车企业在手套箱旁布置阻尼器来降低打开速度,避免开箱过快。常规阻尼器包括空气拉线/拉杆阻尼器[1]、硅油齿轮齿条阻尼器[2]。部分汽车企业和零部件厂商开发了具有速度反馈功能的新型阻尼器[3],使手套箱在不同负载工况下打开时间的差异减小。
但是,阻尼器只是手套箱开启性能的影响因素之一,且各阻尼器方案都不能为前期手套箱的结构设计提供运动性能评价依据;同时,目前验证手套箱运动性能的手段也局限在实物样件注塑成型后的装配总成测试。造成这一问题的原因,一是手套箱打开的动力学过程相对复杂,二是现有内饰零件设计规范中缺乏相关设计指南。因此,在设计前期分析手套箱打开时间非常重要。
针对以上需求,本文对手套箱打开过程进行动力学分析,建立打开角度与打开时间的函数关系并在Excel软件上实现其数值求解。可据此时间预判来优化手套箱总成的质量分布、转轴位置、储物径深等结构参数,及阻尼器紧固位置、作用挂点位置等布置参数,实现在前期对手套箱系统的运动性能进行精确设计。
2 理论计算
手套箱关闭与开启状态之间的运动转换是复杂的动力学过程,但如果其转轴是水平方向布置的,则可将力学模型简化到一个与转轴垂直的竖直平面中,如图1所示,该旋转运动中手套箱自身重力与负载重力产生顺时针方向的力矩,阻尼器的阻滞牵引力产生逆时针方向的阻力力矩。两者合力矩决定了系统的转动性能,即可用牛顿第三定律力矩方程来表征开箱转动过程:
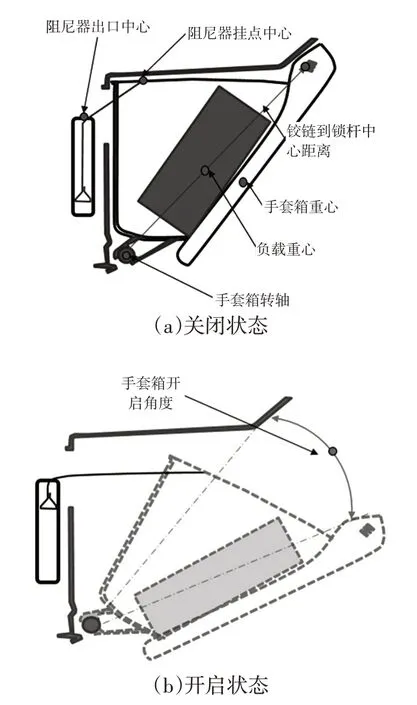
图1 手套箱系统开闭状态示意

式中,∑M为合力矩;I为转动惯量;ω为刚体转动角速度;t为时间。
假设转动过程中手套箱自身结构未发生相对形变,箱内的负载重物与内斗相对位置也未发生改变,可将该转动系统视为刚体,用手套箱自身质量(可运动部分机构的质量)及负载质量的综合质心替代模型来表征总的转动惯量:

式中,m为手套箱与负载的总质量;r1为综合质心到转轴的距离,即质心的旋转半径。
以采用拉线阻尼器的手套箱为例,其开闭状态见图1,外壳固定于手套箱框背部。开箱时拉线从出口端被抽出,内斗中的负载用矩形物体模拟。
为了便于对力矩量化表达,在质心(重心)所在竖直平面内建立直角坐标系:以转轴位置为原点、水平向车后为X轴正方向、竖直向上为Z轴正方向,如图2所示。图中a0为手套箱起始时自重重心位置,为负载重心位置,A0为手套箱与负载两者的坐标值以各自质量为权重的加权平均位置,P为阻尼器拉线出口端中心位置,在开启过程中保持固定;C为阻尼器拉线的另一端系挂在手套箱内斗(简称挂点)的位置。图2 显示了挂点在运动起始时的位置C0和开箱终止时的位置C1。
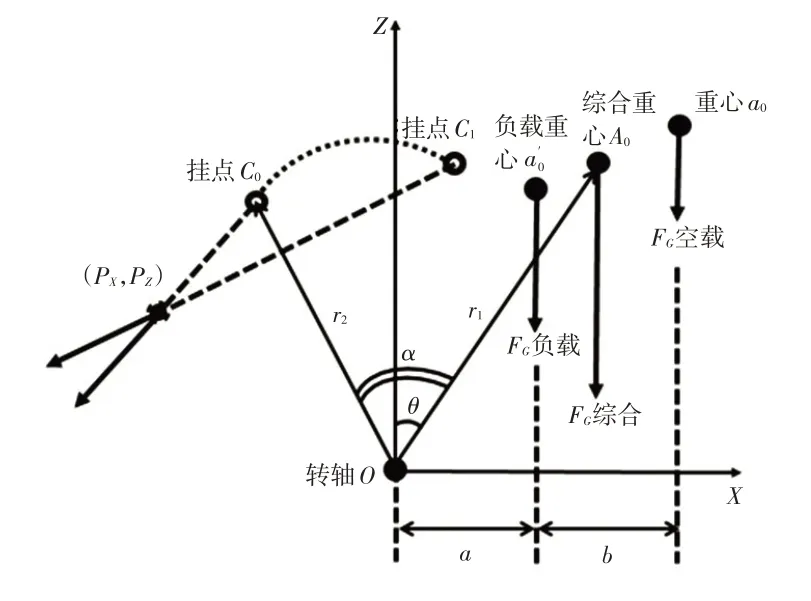
图2 手套箱XOZ平面直角坐标系
将∑M用力与力臂乘积的代数和表示,ω用手套箱质心角度θ对时间t求导表示,并将式(2)代入式(1)得到:
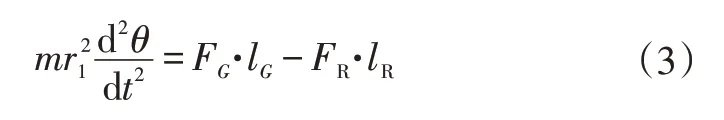
式中,FG为手套箱及负载的总重力;lG为重力FG的力臂;FR、lR分别为阻尼器提供的阻力及其力臂。
式(3)中阻力由阻尼器提供,不同厂商/型号阻尼器的阻滞效果各不相同,本文使用一种多项式力学模型表征各种阻尼器的阻滞力效果:
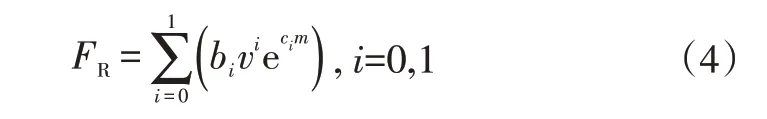
式中,v为手套箱转动系统质心处的线速度;bi、ci为阻尼器特征参数。
i=0时,多项式的0阶式表达为b0ec0m,b0表征阻尼器在稳定拉线/拉杆时提供的阻力,ec0m表征该阻力随转动系统总质量的增减进行的修正(空气拉线/拉杆阻尼尤其有这种特性)。i=1时,多项式的1阶式表达为b1vec1m,表示阻尼器的阻力受转动速度v和总质量m的影响。不同阻尼器的特征参数bi、ci可通过拉伸测试得出。图2中P、C的连线方向即阻力的作用方向,可通过平面几何计算lR的代数表达式。
将式(4)及lG、lR的表达代入式(3),整理后得:
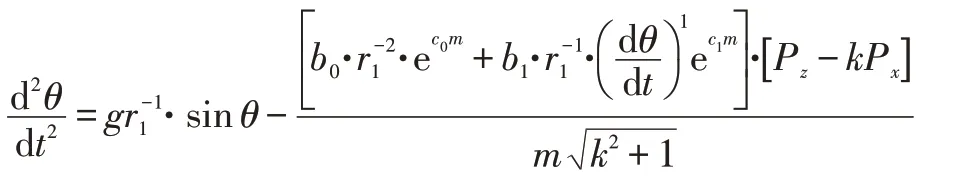

式中,g为重力加速度;(Px,Pz)为出口端中心点P在XOZ坐标系下的坐标;r2为点C到转轴O的距离;α为OA0与OC的夹角;k=(Cz-Pz)/(Cx-Px)为点C与点P连线的斜率;Cx=r2sin(θ-α)、Cz=r2cos(θ-α)为挂点C的坐标。
式(5)建立了手套箱转动系统的质心旋转角度θ与时间t之间的函数关系,其中仅有1 个变量t,为二阶常微分方程。由于其一阶导数角速度ω(t)、二阶导数角加速度ω′(t)都存在,其难以求得解析解。但如果能求解出θ与t的数值解,已足以支持在前期开发中对手套箱系统的运动性能进行设计。
3 理论计算与物理试验
为了便于使用,本文尝试在Excel 上对该微分方程进行数值求解。
Excel的自动填充功能为微分方程的分步计算提供了快速迭代的软件基础;而龙格-库塔(Runge-Kutta)法则提供了一种高精度单步迭代算法,其中经典四阶法(RK4)最为常用[4-5],设置算法时间步长为h=0.02 s,函数θ(t)第(i+1)步的值可以从第i步出发计算得到。从而在Excel软件中利用单元格的自动填充功能将RK4的迭代公式内容扩充,实现微分方程数值解的便捷计算。
选取某些已量产车型的仪表板手套箱作为研究对象,在Excel 软件中通过上述RK4迭代法数值求解这些车型的手套箱打开时间,同时,在实车上测试并记录打开时间,两者结果如表1所示。
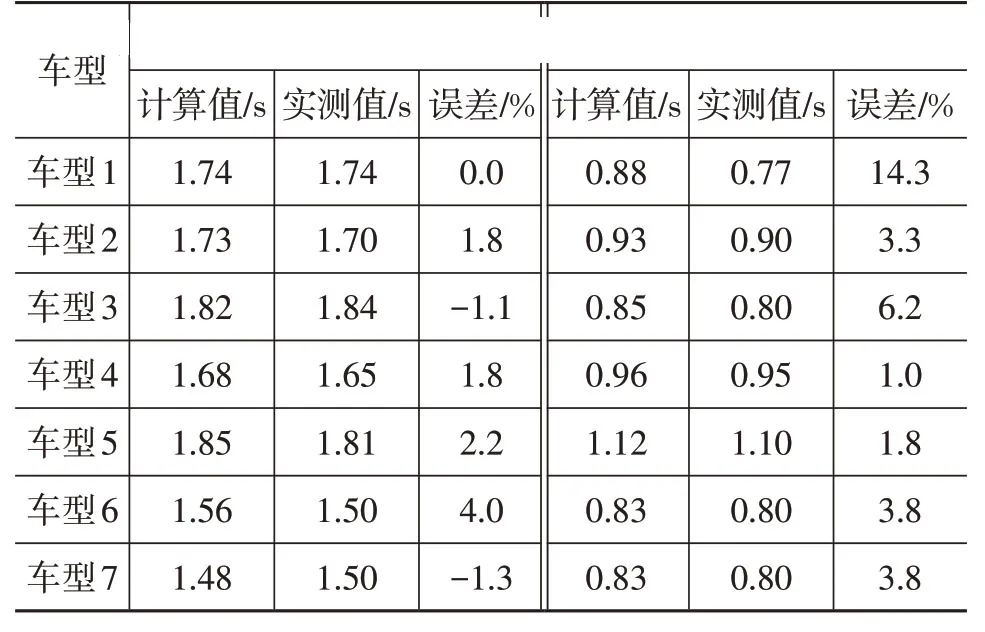
表1 部分车型手套箱打开时间计算与测试结果
实车上手套箱打开时间t按以下要求测试:
a.使用非接触的自动计时器,如光栅自动停表装置。时间测量起始点为手套箱开始移动时,终止点为完全打开状态。在这两处布置感应光栅,控制计时。
b.测试时解锁手套箱的锁止机构,但仍保持手套箱在完全闭合状态。
c.至少选取3 个样件,记录每个样件的结果并计算平均值。
由表1 可知,在空载和负载2 kg 工况下,计算得到的手套箱打开时间在所有测试车型中都取得了与实车相近的结果。故本文提出的算法可在手套箱区域零件前期开发阶段预判,优化结构和布置。
4 打开时间影响因素分析
4.1 手套箱结构设计
式(3)中∑M包含重力力矩和阻力力矩。重力力矩方面,因刚体自重在运动中保持不变,故重点讨论lG,分别定义负载重心X轴坐标值为参数a、手套箱转动部分自重重心X轴坐标值与负载重心X轴坐标值之差为参数b,见图2。
参数a表征负载在手套箱内斗中的摆放位置与内斗转轴结构的距离关系;参数b表征转动部分的自重在手套箱外板的集中情况。这样将lG拆分定义为一对参数组合,可分别分析手套箱内部结构对运动性能的影响。利用本文计算工具计算不同a、b取值组合与空载打开时间、负载2 kg打开时间的关系,如图3、图4所示。
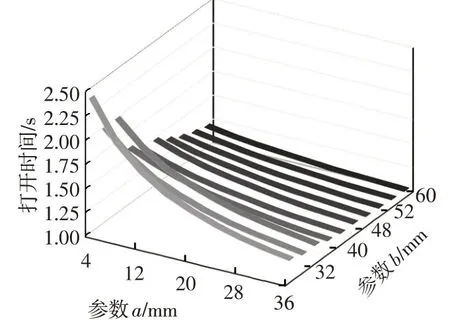
图3 空载工况参数a、b对打开时间的影响
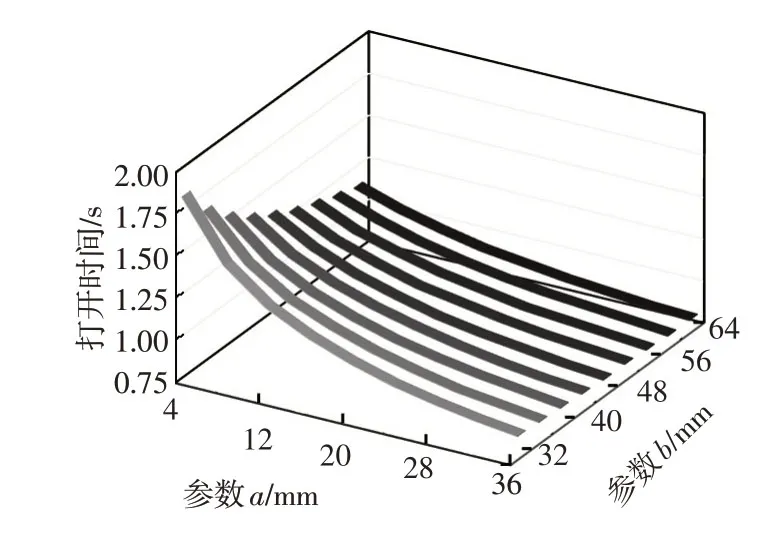
图4 负载工况参数a、b对打开时间的影响
由图3可知,空载条件下,当重力力臂(a+b)<50 mm时,打开时间随(a+b)的减小而迅速延长,甚至出现力臂过小、手套箱自身重力力矩不足导致无法开启的趋势,故转轴应避免过于靠近手套箱自身重心。由图4可知,加载2 kg重物条件下,打开时间也随(a+b)的减小而增大,且a对时间的影响比b更显著,这是因为手套箱转动部分质量约为1 kg,所以2 kg负载贡献的力矩相对更大。
将图3、图4的结果作时间变化率的计算,即负载打开时间与空载打开时间的差值与空载打开时间的比值,引出时间损失比的概念,描述手套箱内放置许多物品的工况下,对开启性能的评价。损失比越接近0,则开启性能越稳健,计算结果统计于图5。
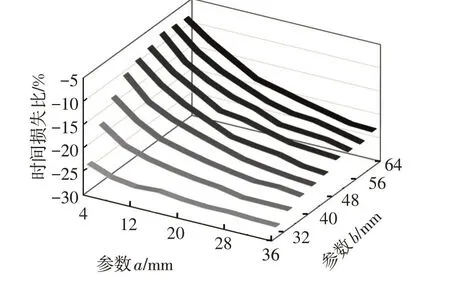
图5 参数a、b对负载打开时间损失比的影响
由图5 可见,损失比曲面都位于负值区,说明无论如何调节a与b,负载条件下打开时间相对空载都会减小。但减小程度在不同a、b 组合下差异很大:b取值较小时,时间损失比基本在-30%~-25%范围内,难以提高优化;而增大b并减小a时,时间损失比可显著改善,尤其在a=4 mm、b≥48 mm的组合范围内,时间损失比可控制在小于10%的范围,差异难以感知。
由图3~图5可归纳手套箱内部结构的设计方法:首先,做深内斗(XOZ坐标系下内斗在X方向的长度大),从而使重物在手套箱内静置于远离外门的位置,且手套箱锁等机构贴近外门板表面放置,两者共同使参数b变大;其次,内斗转轴结构的水平位置尽量贴近负载重心且偏车前设计,这样既能保证手套箱可凭借自身重力打开,也能使参数a较小。
4.2 阻尼器布置设计
选定某款阻尼器后,其多项式力学模型也随之确定,故同样重点讨论力臂。lR由PC连线即阻尼器的布置设计决定。如图6 所示,在XOZ坐标系第二象限内,通过固定点P、移动点C的方式改变PC连线的方向,从而实现对lR的调节。
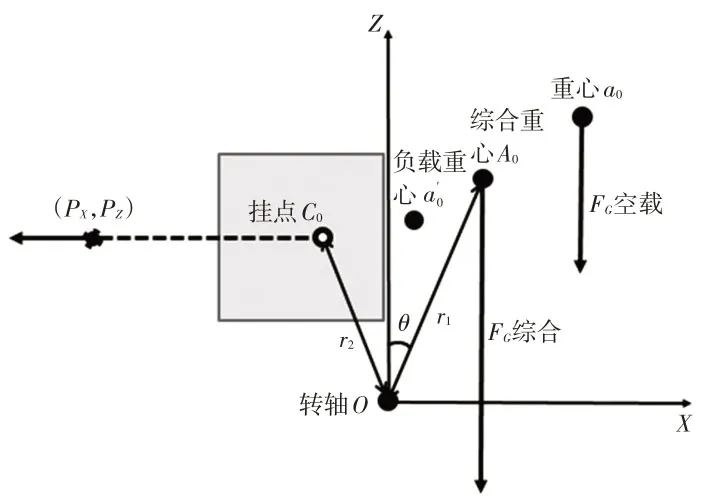
图6 挂点坐标(Cx,Cz)的研究范围示意
如图6所示,在Z轴左侧50 mm、P点高度±25 mm的矩形范围内移动C点,其基本覆盖了lR的可变区间。通过调节Cx与Cz的赋值即可统计阻尼器布置设计对空载打开时间、负载打开时间和时间损失比的影响,如图7~图9所示。此外,a0与的位置选取参考了图5中时间损失比<10%区域的结果:选取a=4 mm、b=56 mm,以研究能否结合结构设计与布置设计来进一步优化时间损失比。
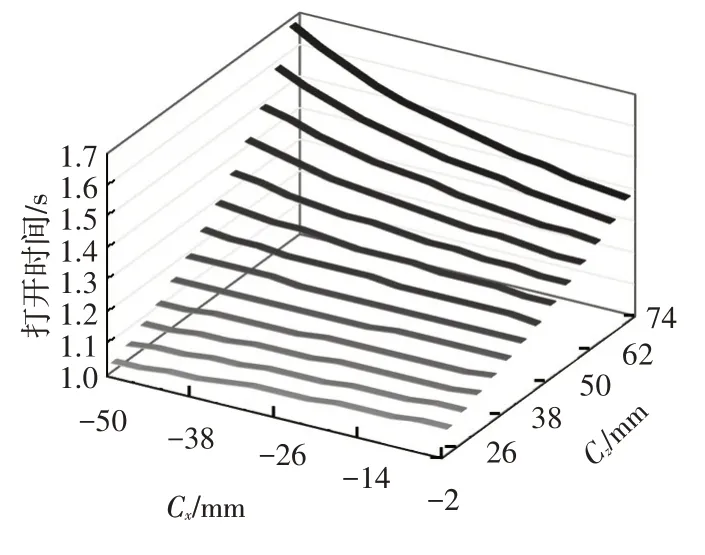
图7 空载工况(Cx,Cz)对打开时间的影响
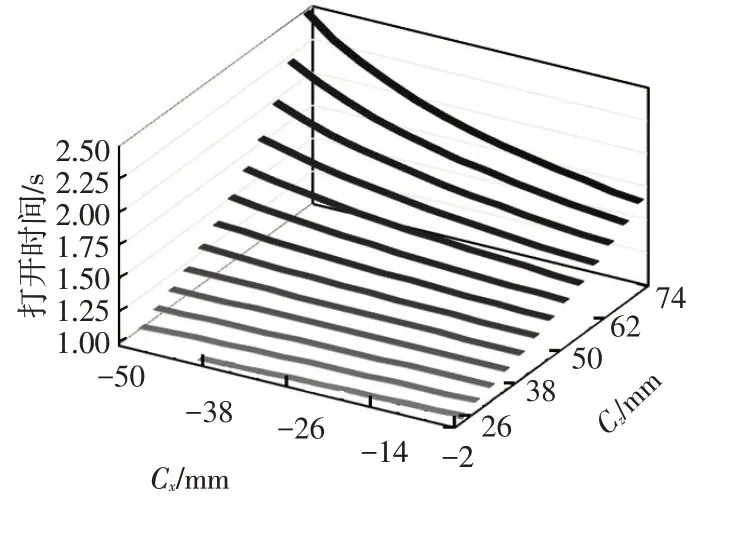
图8 负载工况(C,C)对打开时间的影响

图9 (Cx,Cz)对负载打开时间损失比的影响
从图7 和8 可知,Cx与Cz显著影响开箱时间,PC连线到转轴点O的距离越大则时间越长。且Cz的影响比Cx更显著:随着Cz由低到高,空载时间跨度从1 s提高到2.5 s,负载2 kg时间从1 s提高到1.7 s;而Cx只有当Cz处于高位时,才对打开时间有明显作用。这主要是因为阻力力臂的大小更取决于挂点的高度,且C点高于P点一定程度后,减小PC之间的水平距离才会显著增大阻力力臂,即出现图7和图8中打开时间在左上角区域显著抬升的现象。
以上结果表明,手套箱内部结构设计和阻尼器布置设计均能有效调节开箱时间。进一步分析两者的结合能否调节开启性能在不同负载工况下的稳定性。图9给出本例中结构设计最优点下,(Cx,Cz)对时间损失比的关系曲面。虽然曲面大部分仍位于负值区,但当Cz低于一定高度时,负载下的打开时间可以与空载持平甚至更长。本例中Cz<30 mm 时(Pz高度的3/5),损失比为0 或为正值。其原因在于:一是开箱过程中,随着挂点向车后侧旋转移动,转轴O到PC连线的垂线长度(即阻力力臂)增加,使阻尼器的阻滞效果更明显;二是综合重力力臂大小在手套箱开启过程中的增量较空载重力力臂的增量小。
由此可归纳阻尼器布置的设计方法:阻尼器外壳,特别是其拉线/拉杆的出口端布置在转轴上方,拉线/拉杆到内斗的系挂点高度位于出口端和转轴之间。同时满足这两点要求可以在使用普通空气阻尼器(阻滞力往往随着负重的增加而减小)的情况下也能实现空载和负载下打开过程保持稳定的手套箱运动系统设计。
5 结束语
本文基于刚体转动动力学理论建立了手套箱系统的转动角度与运动时间的函数关系,并使用龙格-库塔四阶法借助Excel 软件实现了迭代计算,便于工程应用。计算结果与实车测试结果误差小,在早期设计阶段即可预判手套箱的运动性能,较常规的经试验设计再优化的方式可大幅缩减开发时间和成本。
最后,采用本文计算工具,探讨了内斗转轴/置物空间、锁止机构和外门板等手套箱内部结构设计与阻尼器固定位置和拉绳挂点位置等布置设计对开启性能的影响,归纳了结构设计与布置设计方法。

