基于极限学习机的质子交换膜燃料电池在线故障诊断方法＊

刘奥 牛志刚 张东光 朱晓鹏 王壮

（太原理工大学，太原 030024）

1 前言

质子交换膜燃料电池（Proton Exchange Membrane Fuel Cell，PEMFC）系统在新能源汽车发展中具有广阔的应用前景。目前，燃料电池的可靠性和寿命是PEMFC 系统大规模商用面临的主要难点之一[1-3]。

PEMFC故障诊断系统的主要功能是检测系统运行中产生的故障，提高系统的运行稳定性和使用寿命[4]。目前，相关研究可分为基于模型的故障诊断和基于数据驱动的故障诊断2 类。基于模型的故障诊断通过建立PEMFC 仿真模型，计算模型输出与实际输出之间的参数偏差，分析残差实现故障检测[5]，包括使用等效电路模型的流阻检测[6]、利用压力降模型的故障诊断[7]、基于线性变参数（Linear Parameter Varying，LPV）模型的非线性动力学仿真[8]和针对膜电极失效的相关研究[9]等。此类诊断方法的难点在于保证模型相对于试验电堆的准确率，由于系统内部数据获取困难，燃料电池系统间存在个体偏差，难以建立准确、具有普遍性的故障诊断模型。基于数据驱动的故障诊断通过算法分析数据建立模型实现故障诊断，快速高效，且无需燃料电池专业知识，具有广阔的研究前景。相关研究包括使用在线序列极限学习机（Online Sequential Extreme Learning Machine，OS-ELM）的故障诊断方法[10]、利用电化学阻抗谱（Electrochemical Impedance Spectroscopy，EIS）的支持向量机（Support Vector Machine，SVM）模式识别[2]、基于小波变换（Wavelet Transform，WT）和奇异值分解（Singular Value Decomposition，SVD）的信号处理方法[11]等。此外，该方法还包括在线诊断的实现，如基于K均值（K-Means）和SVM的在线自适应故障诊断[12]。

以上研究仍存在待解决的问题：SVM 受Mercer 条件限制，收敛慢；神经网络复杂度高，对样本、算力需求大，存在过拟合、局部极小值等问题；主成分分析（Prin⁃cipal Component Analysis，PCA）降维时面对复杂特征聚类准确率较低；增量学习算法的引入研究仅探讨了算法本身的可行性，未考虑诊断模型更新的实现。

针对以上问题，本文提出基于在线序列极限学习机和无监督极限学习机（Unsupervised Extreme Learn⁃ing Machines，US-ELM）的燃料电池在线故障诊断方法，引入US-ELM 得到反映燃料电池系统运行状态的特征向量，使用OS-ELM 对特征向量进行分类，在数据获取方面，采用K-Means 聚类区分正常与故障状态的数据，并使用包含3 种不同状态的样本对方法的有效性进行验证。

2 蒸发冷却型燃料电池系统与算法原理

2.1 蒸发冷却型质子交换膜燃料电池

蒸发冷却（Evaporatively Cooled，EC）型燃料电池系统是由英国智能能源公司针对高容量、低成本的工业需求设计的PEMFC。其100 kW EC型PEMFC电堆可提供3.5 kW/L 及3.0 W/kg 的功率密度，EC 技术利用蒸发冷却替代传统的冷却液循环，无需设置冷却水流道，降低了系统的复杂性、质量和生产成本。系统原理如图1所示，系统并联了2 台PEMFC 电堆，分别由300 片单电池组成，空气和氢气分别输入到电池的阴极和阳极，液态冷却水输入到电堆，部分蒸发形成液体/蒸汽混合物并从电堆中带走热量，为保持系统水量平衡，热交换器会将电堆排出的蒸汽冷凝，将水收集并送回水箱。

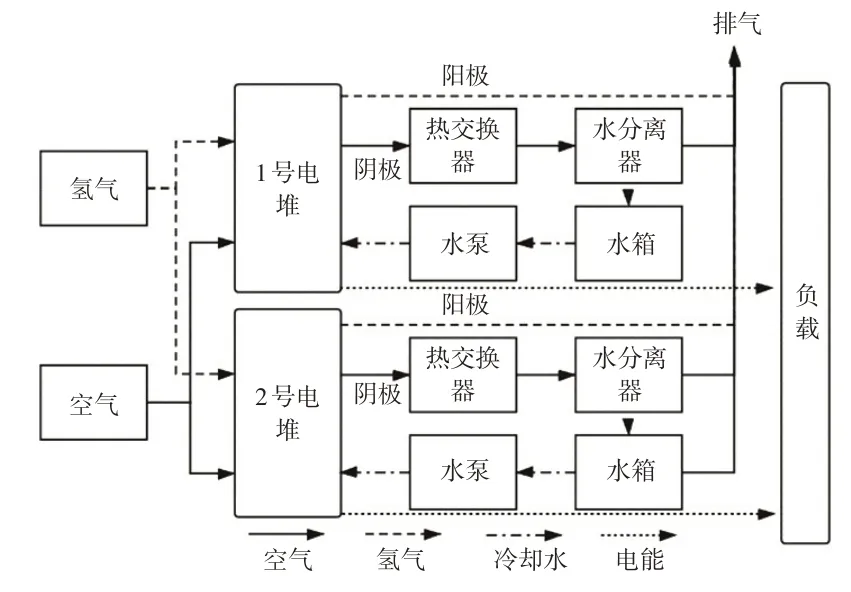
图1 EC型燃料电池系统原理

2.2 在线学习故障诊断系统算法

2.2.1 极限学习机

极限学习机（Extreme Learning Machine，ELM）[13]是基于广义逆矩阵的新型单隐层前馈神经网络，该网络由输入层、隐含层和输出层构成，原理如图2所示。

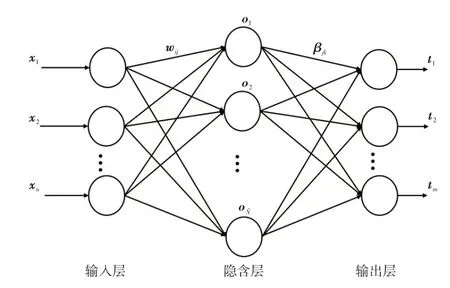
图2 ELM网络结构示意

设数据集为ℵ={(xi,ti)|xi∈Rn,ti∈Rm,i=1,…,N}，隐含层神经元数量为，隐含层激励函数为g(x)。数据集输入样本可表达为xi=(xi1,xi2,…,xin)T∈Rn，输出目标可表述为ti=(ti1,ti2,…,tim)T∈Rm。ELM的输出矩阵O为：

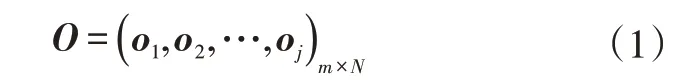
其中，oj为隐含层神经网络节点：

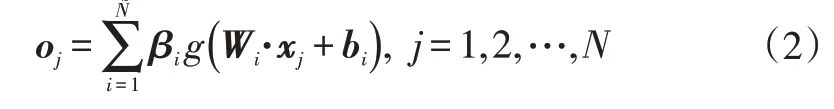
式中，Wi=(wi1,wi2,…,wim)T为输入权重，即第i个隐含层节点与输入层间的连接权重矩阵；βi=(βi1,βi2,…,βim)T为输出权重，即输出层与第i个隐含层间的连接权重矩阵；bi=(bi1,bi2,…,bim)T为第i个隐含层的偏置矩阵。

ELM 的学习目标是使输出误差尽量接近于零，可表述为：

若隐含层神经元数量与训练集样本数量相等，ELM对任意隐含层输入权重和偏置均能实现零误差逼近。然而，实际操作中训练样本数量常大于隐含层节点数量，训练误差可逼近任意ε>0。

结合式（1），学习目标可表述为矩阵形式：

式中，T为期望输出；β为输出权重矩阵；H为极限学习机隐含层输出矩阵：

式中，H†=(HTH)-1HT为H的穆尔-彭罗斯（Moore-Penrose）广义逆矩阵[10]，该解范数唯一且最小。

2.2.1.1 无监督极限学习机

US-ELM利用了ELM的逼近能力，通过非线性映射将原数据投影到低维空间，利用高斯函数描述近邻样本间的相似度，并得到显式的非线性映射函数[14]。US-ELM 继承了ELM 的计算效率和学习能力，可用于多分类或多聚类，在精度和效率方面都满足使用需求，在降维任务中，设训练数据为X∈RN×ni，其输出目标为n维空间中的嵌入矩阵E∈RN×n0（ni为训练数据维度，n0为嵌入矩阵维度）。运算流程如下[15]：

a.基于原始数据X，构建拉普拉斯（Laplacian）参数L。

b.利用随机输入权值构建隐含层神经元数量为nh的ELM 网络，并计算隐含层神经元H∈RN×nh的输出矩阵。

c.US-ELM目标函数为：

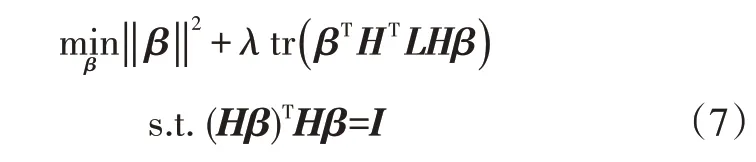
通过将β作为矩阵给出式（7）的最优解，该求解过程可替换为广义特征值问题的求解，根据nh与N关系式（7）进行如下替换：

若nh≤N，式（7）可替换为(Inh+λHTLH)νs=γsHTHνs,s=1,2,…,n0+1，γs(γ1≤γ2≤…≤γn0+1)为最小特征值，对应特征向量vs，使，其中,i=2,…,n0+1为归一化特征向量；

若nh＞N，式（7）可替换为(Inh+λLHHT)us=γsHHus,s=1,2,…,n0+1，γs(γ1≤γ2≤…≤γn0+1)为最小特征值，对应特征向量us，使，其中,…,n0+1为归一化特征向量。

d.计算嵌入矩阵E=Hβ。

2.2.1.2 在线序列极限学习机

当样本数据分批次加入时，传统ELM 需要重新训练模型。为适应增量学习需求，Liang 等在ELM 的基础上提出了OS-ELM 算法[16]。OS-ELM 的学习过程分为初始和在线学习2 个阶段，先通过少量样本得到OS-ELM 的初始输出权重β0，再利用新样本/数据块更新β0。

2.2.1.2.1 初始阶段

设有N0个训练样本ℵ0={(xi,ti)|xi∈Rn,ti∈Rm,i=1,…,N0}，其中N0≥。运算流程如下：

a.产生随机的输入权重矩阵wi和偏置矩阵bi，其中i=1,2,…,。

b.计算初始隐含层输出矩阵H0。

c.计算初始输出权重矩阵β0：

d.令数据块（Block）序号为k=0，初始化阶段完成。

2.2.1.2.2 在线学习阶段

在线学习阶段每次投入样本为1 个Block，每个Block包含若干样本(xi,ti)。设 第(k+1)个Block的样本，在Block 中的样本数大于1 时，运算流程如下：

a.计算隐含层输出矩阵Hk+1。

b.计算输出权重矩阵βk+1：

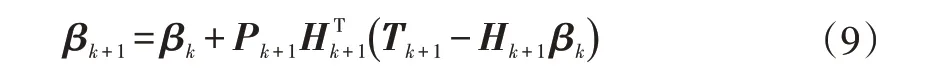
c.令k自加1，重复在线学习阶段，直至完成全部学习。

2.2.2 K-Means聚类算法

K-Means 是一种基于距离的经典聚类算法，因其快速、简单而得到广泛使用。设数据集X=[xi],xi∈Rd,i=1,2,…,k，其中k为样本数量，d为样本维数，样本的类别空间a=[aj],aj∈Rm,j=1,2,…,l，其中l为类别数量。样本点距离度量采用欧氏距离：

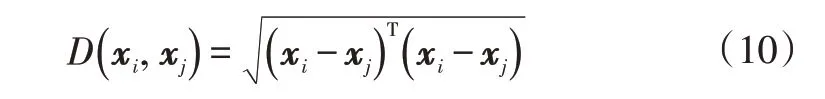
聚类中心为：

式中，kj为属于第j类的样本数量。

K-Means的目标是使簇内样本距离最小，簇间样本距离最大化，其目标函数为：

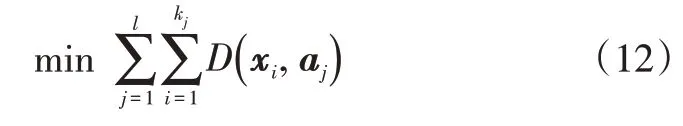
算法迭代的时间复杂度为O(tldk)，空间复杂度为O((k+c)d)，其中t为迭代次数，一般t、c均不大于n[12]。

3 基于OS-ELM的在线学习故障诊断系统

现有的大部分基于数据驱动的诊断方法中，训练好的诊断模型不再做进一步调整，当故障出现新的特征时，只能重新训练模型，虽然有文献探讨了增量学习在故障诊断领域的应用，但在故障特征提取等方面并没有考虑新数据的获取过程。

为解决增量学习过程中的样本获取问题，本文提出使用US-ELM 和K-Means 构建基于OS-ELM 的在线故障诊断方法，利用OS-ELM的增量学习能力构建诊断模型，US-ELM实现基于流形正则的降维并输出显式的降维函数。由于数据采集和旧模型的分类往往无法标记全部数据，故引入K-Means 聚类算法，利用不同状态数据聚类准确率较高的特点，在进行少量人工标记的情况下达到批量区分标记新数据的目的。图3 所示为使用该方法进行燃料电池系统故障诊断的流程。

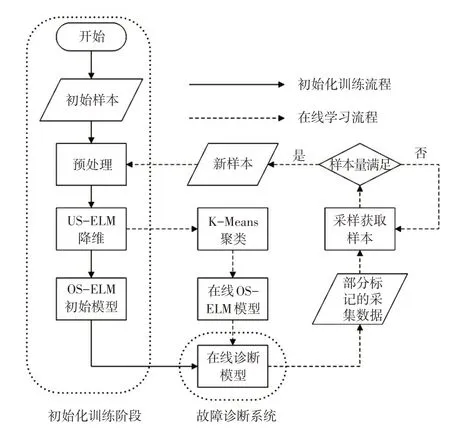
图3 在线诊断模型流程

在系统流程中，预处理步骤包含在US-ELM算法程序内，K-Means 聚类用于辅助新样本的数据划分，根据研究经验，US-ELM 降维后数据的聚类效果明显，故利用聚类辅助区分，根据诊断系统的部分预标记对各聚类区块进行标记。另外，在整个流程中，初始的在线诊断模型由OS-ELM初始模型提供，之后均由在线OS-ELM模型提供，该在线OS-ELM模型即为在线学习阶段通过新样本更新的OS-ELM初始模型。

4 实例分析

4.1 原始数据获取

为验证本文提出的方法，利用正常状态、膜干故障和阳极缺气故障共3 种状态的数据验证算法的诊断效果。由蒸发冷却型PEMFC 获得的原始数据共有约182 130 组，其中正常状态（Normal）171 020 组，阳极缺气故障（F1）2 604组，膜干故障（F2）8 506组，2种故障对电堆的影响如下：

a.膜干故障。质子交换膜为保持良好的离子导电性，运行状态下需要与水接触以保持较高的相对湿度，否则产生膜干故障会导致膜的欧姆阻抗变化[17]，极大地影响质子传导率，引起欧姆过电势增加和电池输出电压下降，严重时会导致电堆内部温度过高，缩短PEMFC使用寿命。

b.阳极缺气故障。阳极缺气会导致电堆无法获得足够的氢气供应，在负载电流下表现为工作电压逐渐下降。严重时，电池电压降至0 后会发生“反极”现象，电池阳极析出氧气，大幅降低电堆的电压。极端条件下，氢氧混合可能会在阴极催化剂上反应发生燃烧，造成燃料电池系统内部爆炸。

考虑机器学习的数据均衡，本实例对每种状态各采样400组数据，从中随机抽取形成训练集、测试集，采样结果数据集各包含样本600组，每个数据集包含3种状态数据各200组，数据的具体参数如表1所示。

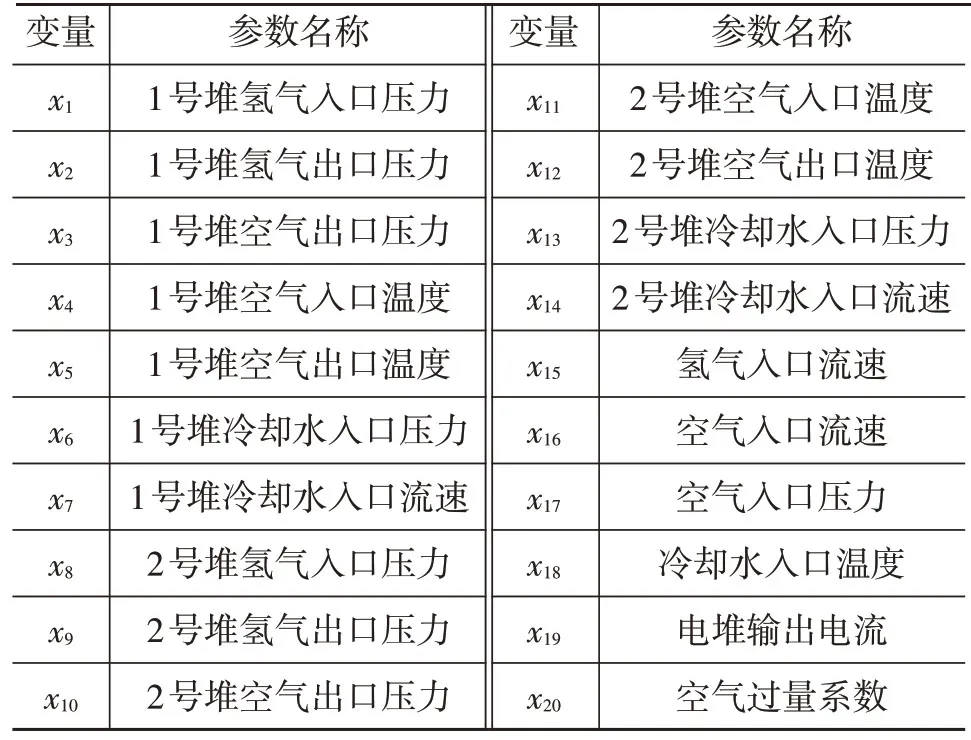
表1 电堆参数

4.2 故障特征提取

为提高聚类和模式识别的效率及准确率，选用US-ELM 对归一化数据进行降维。US-ELM 降维基于流形正则思想，利用ELM 的逼近能力将高维样本通过非线性映射投影至低维空间，并能够得到显式的映射函数[14]。在保证降维数据各维度的相关性尽量最小的同时，通过将高维数据合理展开至低维空间，可大幅简化模型复杂度。

由表1 可知，每组原始数据为1 个20 维特征向量X=(x1,x2,…,x20)，对样本进行归一化处理，将向量中各变量归一化至[-1,1]区间，在保留数据特征的同时减少了量纲差异所带来的问题。

由于非线性降维的参数选取缺乏统一的评判指标，本文以US-ELM 在不同参数下的聚类准确率作为衡量标准，对比并最终确定特征提取的参数设置如下：拉普拉斯算子采用基于距离的权重，距离度量采用欧氏距离函数，算子归一化参数为0，迭代阶数为1 阶，近邻数量为5个，超参数设定嵌入层数为5层，隐含层神经元数量默认为2 000 个，归一化输入、输出均为1，核函数使用Sigmoid函数。降维后部分样本数据如表2所示。

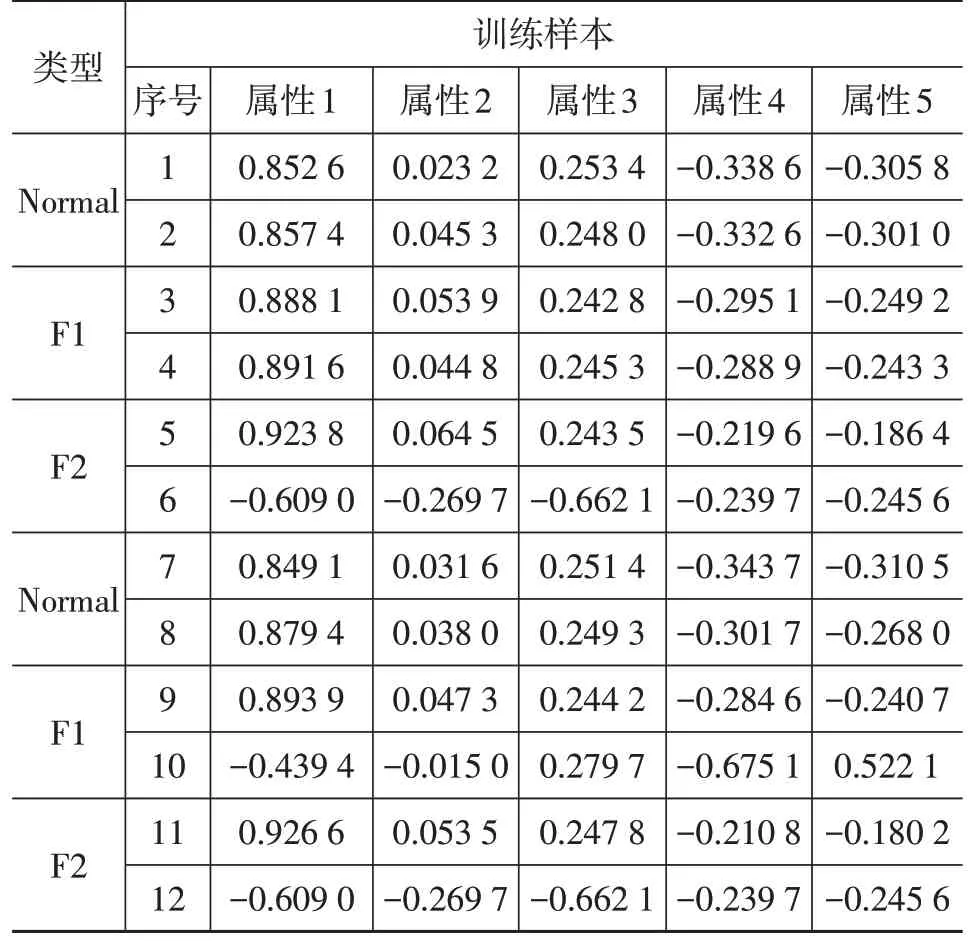
表2 US-ELM降维后的部分训练样本和测试样本

4.3 OS-ELM初始阶段

OS-ELM初始阶段，算法参数包括初始训练数据量N0=200 组，隐含层神经元数量L=5 个（考虑预处理后数据维度），激活函数使用Sigmoid函数。该阶段对应OSELM 的初始模型生成。在系统流程中，该步骤生成的模型即可用作最初的在线诊断模型，对后续试验中获得的数据进行故障识别及标记。

4.4 在线学习阶段的数据划分

该步骤用于标记经预处理的原始数据，此时数据缺少状态标签（正常或故障），需对新数据进行聚类和标记。使用K-Means算法，基于诊断模型的结果和少量人工标记，即可实现快速分类获得不同状态的数据，形成新的训练集，配合增量算法实现诊断模型的更新。

为更好地验证聚类结果，将试验样本合并后进行K-Means 聚类分析，可视化结果如图4 所示，经降维后数据的聚类准确率达95.75%，较原始样本提升约12.5%，其中正常状态数据的聚类准确率达到100%，可达到快速有效分离各状态数据的目的。

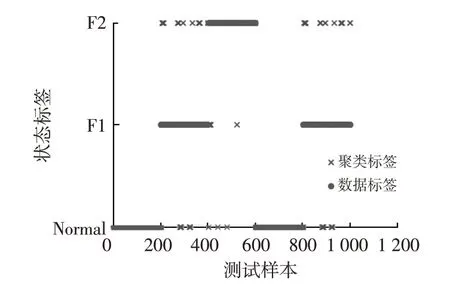
图4 K-Means的聚类结果

在聚类过程中，存在少量样本标记错误的情况，由于诊断模型的更新在原模型基础上产生，新样本数量远少于模型累计训练样本的数量，因此这类错误并不会影响更新后新模型的诊断准确率。

4.5 在线学习阶段及验证

OS-ELM 在线学习阶段，隐含层神经元数量L=5个（考虑预处理后数据维度），激活函数使用Sigmoid函数，以上参数需与初始阶段保持一致。数据块为40组，表示未训练样本将以40组为1个数据块投入模型模拟增量学习过程，在初始阶段的基础上对模型进行更新。试验结果的分布如图5所示，OS-ELM的运算用时为0.187 5 s，训练样本分类准确率为93.17%，测试样本分类准确率为92.00%，其中正常状态的分类准确率达100%。

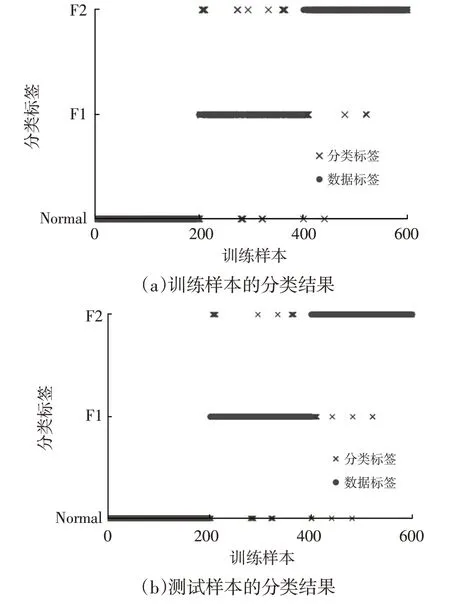
图5 US-ELM-OS-ELM的分类结果

基于US-ELM-OS-ELM 的燃料电池系统诊断结果如表3 所示。由表3 可以看出，US-ELM-OS-ELM 的准确率均达到90%以上，整体准确率为92%，分类诊断效果较好。

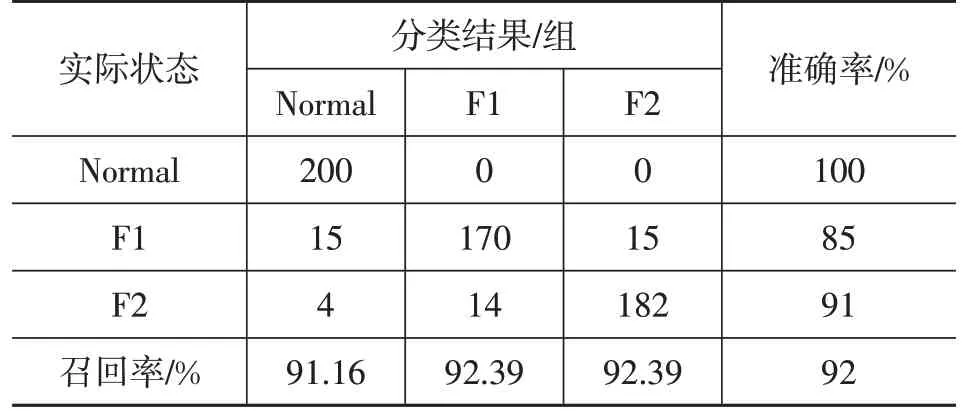
表3 基于US-ELM-OS-ELM的燃料电池系统诊断结果

试验结果验证了US-ELM-OS-ELM 构建模型的故障诊断能力，此外，结果较PCA-OS-ELM得到的同维数样本准确率提高约6.97%，且达到相近准确率所用的L数值更小，说明US-ELM用于特征提取在改善K-Means聚类效果的同时，对模型复杂度的降低能力更好。

试验验证了使用US-ELM 和K-Means 建立以OSELM为核心的在线学习诊断模型的可行性。由于试验的主要目的为检验聚类辅助数据标记的可行性和算法的在线学习能力，样本偏重表现数据特征的复杂度，导致在样本总量有限的情况下部分特征独立出现，对分类准确率产生了较大影响，OS-ELM的分类准确率略低于预期。本文认为随着增量学习的进一步深入，该影响会随着训练数据的增加得到改善，OS-ELM 相关文献[10]表明，在各特征样本数量充足的情况下，OS-ELM 准确率、召回度均可达98%以上，且性能优于SVM、反向传播（Back Propagation，BP）等同类算法。

5 结束语

本文利用蒸发冷却型燃料电池系统数据进行了故障诊断研究，提出了在OS-ELM基础上使用US-ELM和K-Means 构建的在线诊断方法，并在试验中实现了对3种运行状态的识别。该方法具有以下优点：

a.US-ELM 实现了非线性的故障特征提取，在样本可视化、聚类及故障诊断等方面均表现了较好的处理结果，提高了聚类结果的准确率并降低了模型复杂度。

b.K-Means 聚类的使用实现了新数据的快速区分，在诊断模型给出结果的基础上能够对大部分数据进行正确分类，扩展了增量学习中旧模型的数据区分范围，降低了增量学习过程中数据标记的困难程度。

c.OS-ELM 作为基于机器学习的诊断方法，在样本数量较少的情况下获得较为可靠的诊断模型，通过增量学习能够不断更新诊断模型并提高诊断性能，具备较高的实用性，并可扩展应用到类似的模式识别问题中。