叶片曲率对少片变截面钢板弹簧力学特性的影响*

杨林 于曰伟 周长城 郑伟

（山东理工大学，淄博 255049）

1 前言

钢板弹簧作为弹性元件兼导向机构，目前广泛应用于乘用车和商用车。随着节能环保、汽车轻量化等相关政策的实施，少片簧以其质量轻、噪声小、性能好、寿命长等优点，日益受到重视。为满足不同工况下的应力约束条件、刚度设计要求和加工工艺需要，少片簧通常加工成抛物线型、斜线型、根部加强型、端部加强型、两端加强型等不同结构型式。针对不同结构型式的少片簧，研究人员建立了相应的少片变截面钢板弹簧刚度、应力计算公式[1-5]。为了使分析结果更加精确，研究人员开始考虑材料[6-10]、片间摩擦[11-14]、安装约束[15-16]等因素的影响，并利用有限元法对少片变截面钢板弹簧的力学特性进行了分析[17-18]，为少片钢板弹簧的前期设计和强度评价提供了科学依据。然而，这些研究均未考虑叶片曲率对少片簧力学特性的影响，不可避免地使设计结果与实际情况存在较大的偏差。

在汽车行驶过程中，少片钢板弹簧除了承受车辆自身及载物质量外，还要承受因路面不平引起的冲击载荷，其主要失效方式是疲劳断裂和产生永久性塑性变形[19]。为在一定程度上减小板簧应力、延长板簧寿命，使各片板簧寿命接近，通常在自由状态下将各片板簧加工成不同的曲率，装配压紧前各片间保持一定自由间隙，装配后各片紧密贴合，呈现自然向上弯曲的状态。但在少片钢板弹簧的设计、分析计算中，往往忽略叶片曲率的影响，将少片簧视为平直的簧片叠加，导致了实际应用时少片簧的性能和寿命难以与设计值相吻合。

为了在现有基础上进一步提高少片变截面钢板弹簧的分析、设计精度，本文通过考虑叶片曲率对少片簧的影响，建立符合少片簧实际结构特征的有限元模型，对不同曲率的少片变截面钢板弹簧的力学特性进行分析，以期为少片钢板弹簧的设计和疲劳寿命预测提供有效的理论参考和技术借鉴。

2 少片变截面钢板弹簧建模与仿真

2.1 结构特征

通常，少片变截面钢板弹簧由1～4 片中间厚两端薄、等宽、等长、曲率半径不同的弹簧钢片叠合而成，其中，少片簧的一半对称结构根据厚度特征划分为3个部分，即根部平直段、变厚度段和端部平直段。为保持等强度特性，变厚度段厚度可按抛物线型或线性变化。板簧中部安装中心螺栓以保证装配时各片的相对位置，形成一根弹性梁纵置于车桥与车架之间，如图1 所示。

图1 少片变截面钢板弹簧

2.2 仿真模型的建立

根据少片变截面钢板弹簧的实际结构尺寸，考虑叶片曲率的影响，利用SolidWorks软件建立相应的少片簧仿真模型。模型简化原则为：

a.考虑到少片簧沿片长方向的对称性，在确保不影响结果精度的前提下，建立钢板弹簧的1/2模型进行仿真。

b.假设板簧在折弯成一定曲率后，各位置的厚度不变。

c.假设第n片板簧与第(n+1)片板簧之间的垫片厚度与第n片板簧端部平直段厚度之和等于第n片板簧根部平直段厚度。

2.2.1 上表面曲线的确定

基于少片簧结构以及设计、安装要求的特殊性，折弯加工前其叶片上表面为水平直线段，折弯成一定曲率后，除根部平直段被骑马螺栓固定仍为直线段外，其余部分变为该片板簧对应曲率圆的一段圆弧，几何关系如图2所示。

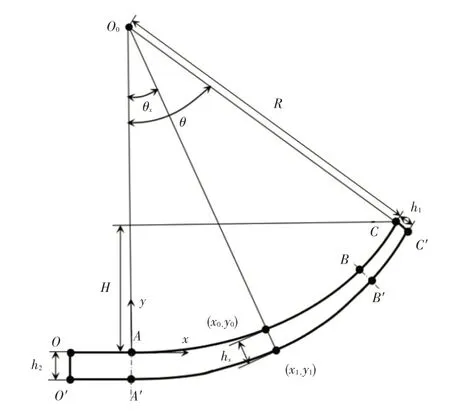
图2 少片簧几何关系

图2中，O0、R分别为板簧上表面曲率圆的圆心和半径，h1、h2分别为板簧端部和根部平直段厚度，直线段OA、直线段O′A′分别为1/2 板簧模型的根部平直段上、下表面曲线，、曲线A′B′分别为模型的变厚度段上、下表面曲线，分别为模型的端部平直段上、下表面曲线，H为弧高，即板簧根部平直段上表面与卷耳下部切线间的垂直距离，θ为对应的圆心角。

由图2可得：

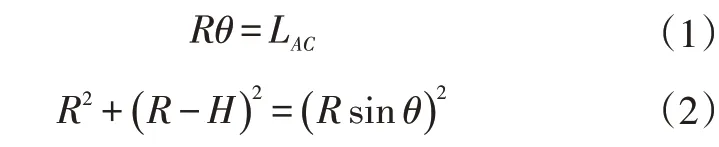
式中，LAC为的长度。

由于各片板簧被压紧且由螺栓固定，根据模型简化原则c，其余各片上表面曲率半径可根据第1片确定。以3片簧为例，设第1片、第2片、第3片叶片上表面曲率半径分别为R1、R2、R3，根部平直段厚度分别为h12、h22、h32，则

2.2.2 下表面曲线的确定

折弯加工后，对应的少片簧的下表面曲线由直线段O′A′、曲线A′B′、组成。其中是以O0为圆心，(R+h1)为半径的一段圆弧。以A为原点，根据简化原则b，曲线A′B′上某点(x1,y1)与曲率圆圆心连线交于点(x0,y0)，点(x0,y0)与点(x1,y1)的连线长度为hx，即折弯加工前点(x1,y1)对应的叶片厚度。利用角度θ建立(x0,y0)与(x1,y1)的关系：

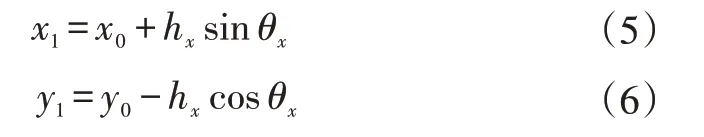
式中，θx为点(x0,y0)与圆心O0连线与垂线O0A的夹角。

运用MATLAB 进行求解，得出曲线A′B′上一系列点，通过对这些点进行8 次曲线拟合，可得到曲线A′B′的表达式。以某片板簧为例，该板簧结构参数如表1所示。

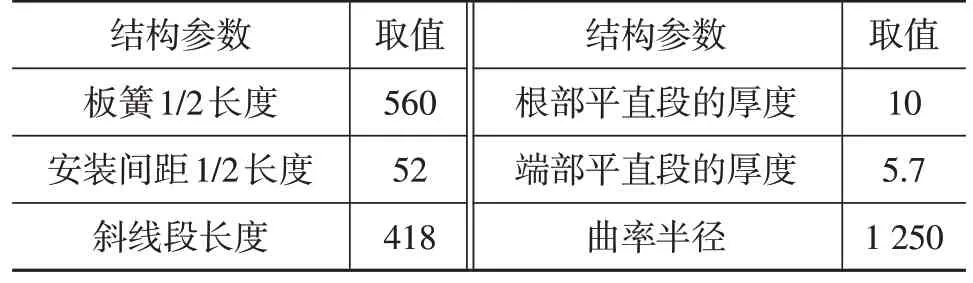
表1 结构参数 mm

所得到的曲线拟合结果如图3 所示。其中曲线A′B′的表达式为：

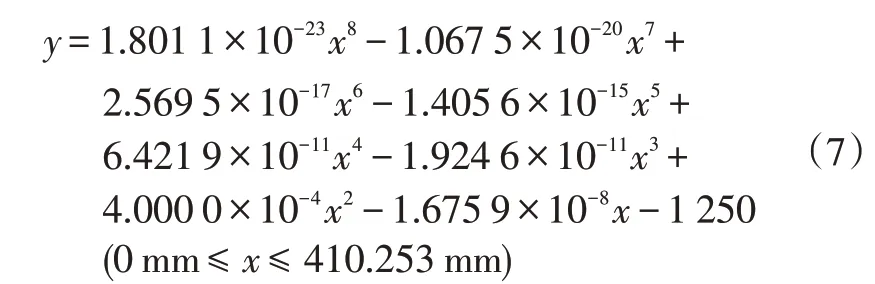
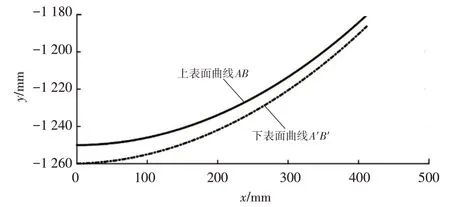
图3 MATLAB曲线拟合

2.2.3 三维模型的建立

将得到的曲线拟合表达式输入SolidWorks软件中，得到少片簧三维模型。

2.3 有限元仿真过程设置

2.3.1 定义单元属性和材料属性

定义单元类型为SOLID186，SOLID186 是一个高阶3维20节点固体结构单元，每个节点有3个分别沿x、y、z方向平移的自由度，支持塑性、超弹性、蠕变、应力钢化、大变形和大应变，三维实体接触单元采用TARGE170及CONTAC174来模拟片与片之间的接触和力的传递。钢板弹簧的材料为60Si2Mn，弹性模量为206 GPa，泊松比为0.29，密度为7.74×103kg/m3，屈服强度为1.176 GPa，抗拉强度为1.274 GPa。

2.3.2 少片簧的网格划分

为提高网格质量，对模型进行合理分块，网格划分主要采用六面体单元，根据板簧结构参数设置合适的单元尺寸来保证计算精度，一般设置为5 mm。

2.3.3 定义边界条件

在两叶片根部平直段、端部平直段分别定义1个接触对来模拟叶片间接触和力的传递，每个接触对都由1个接触面和1 个目标面组成，定义凸曲面为接触面，凹曲面为目标面，接触类型定义为摩擦接触，按簧片在良好的润滑状况下计算，摩擦因数设置为0.2，接触刚度系数为0.001。由于各叶片之间采用中心螺栓连接且在钢板弹簧中部用U形骑马螺栓夹紧在桥壳或桥体上，故在各叶片根部施加宽度方向上的固定约束，各叶片的端部为自由端，允许其自由变形。

2.3.4 加载-卸载和求解

集中载荷加载在首片少片簧端部的节线上，为了获得不同载荷下少片簧的变形，以分步加载的方式施加载荷，加载过程分解为7 个载荷步，逐级加载至最大载荷5 280 N。卸载过程同样分为7 个载荷步，逐级卸载至空载。由于少片簧在受力过程中产生大变形，故打开求解控制中的几何大变形选项。因板簧间的接触的特点为不穿透、自由的分离和带摩擦的滑移，故关闭修剪接触（Trim Contact）并选择接触算法为罚函数法（Pure Penalty），以提高计算准确性。添加总位移分布云图（Total Deformation）和应力分布云图（Equivalent Stress）分析求解。

3 模型试验验证

以某少片斜线型变截面钢板弹簧为例，对所提出的建模方法的正确性进行试验验证。该少片簧的结构参数如表2所示。

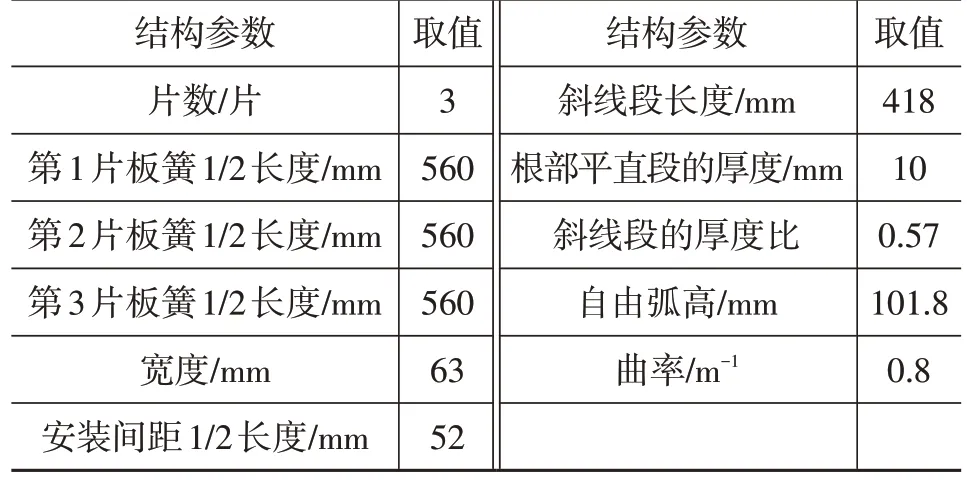
表2 结构参数

3.1 ANSYS仿真

根据所建立的仿真模型搭建方法，构建的少片斜线型变截面钢板弹簧仿真模型如图4所示。

图4 仿真模型

利用ANSYS有限元分析软件对该少片簧进行静力学特性仿真，通过解算器输出检查，确定该有限元模型共计52 422个节点、12 103个单元。

3.2 试验结果与仿真结果对比

根据GB/T 19844—2018所规定的试验方法，对表2所示少片簧进行力学特性试验，试验测试设备为TPW-100 型钢板弹簧静刚度试验机，试验平台如图5 所示。试验中，逐级对该少片簧进行加载和卸载，测试少片簧的变形和应力等参数。通过有限元软件对曲率k为0和0.8 的板簧模型进行加载-卸载仿真，所得到的试验数据与仿真数据对比结果如图6所示，力学特性对比结果如表3所示。

图5 试验平台和测试过程

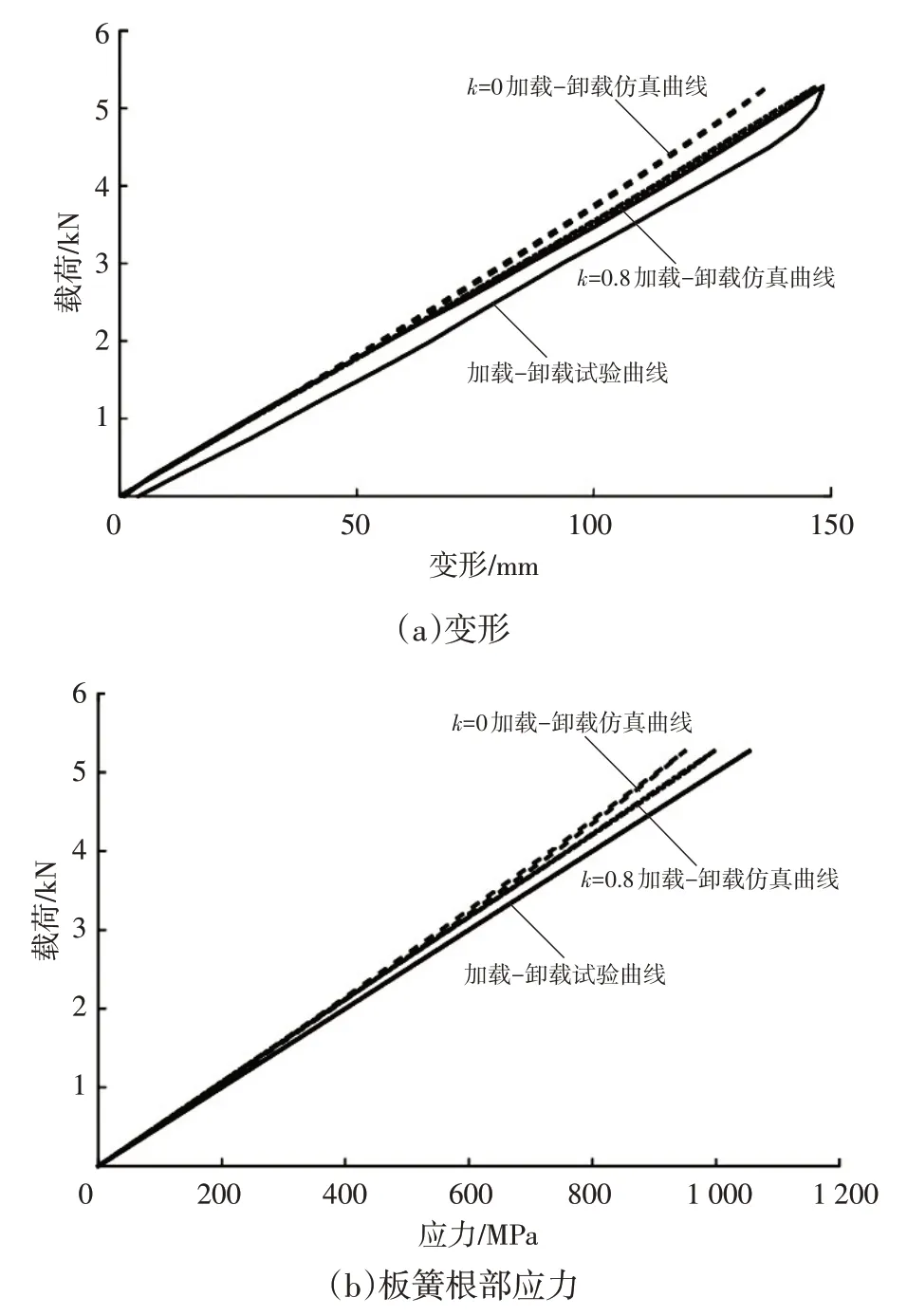
图6 试验与仿真对比结果

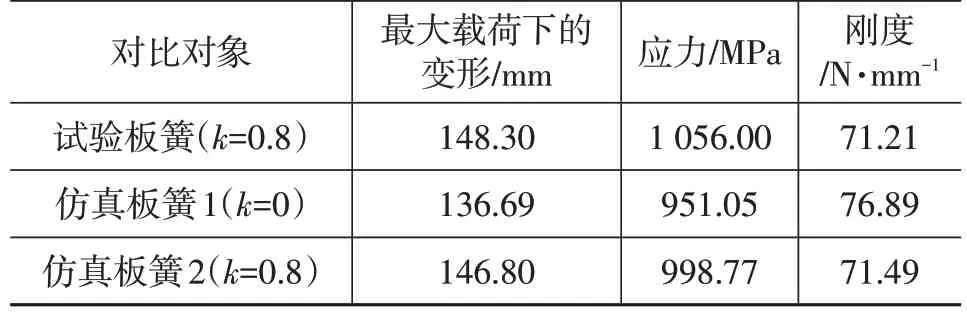
表3 力学特性对比结果

由图6和表3可知，加载至最大载荷时，仿真板簧1与仿真板簧2 的变形与试验结果的相对偏差分别为7.8%和1.0%，对加载过程的变形曲线进行线性拟合，得到刚度数据，仿真板簧1与仿真板簧2的刚度与试验值的相对偏差分别为7.987%和0.403%。结果表明，仿真板簧2与试验板簧刚度吻合度较高，即建模时考虑曲率能够较好地反映少片簧的刚度特性。产生相对偏差的主要原因在于：建模时忽略了实际板簧在由平直状态折弯成一定曲率的过程中因受拉力、压力而造成的叶片厚度变化。加载至最大载荷时，仿真板簧1 与仿真板簧2的最大应力均出现在板簧根部，与试验结果的相对偏差分别为9.94%和7.83%，由于仿真时没有考虑装配所产生的应力，导致应力仿真结果小于试验结果，为准确模拟该曲率板簧在装配和受压后的应力情况，对装配过程进行仿真，在考虑装配、加载、卸载3 个阶段后，得出的应力对比结果如图7所示。

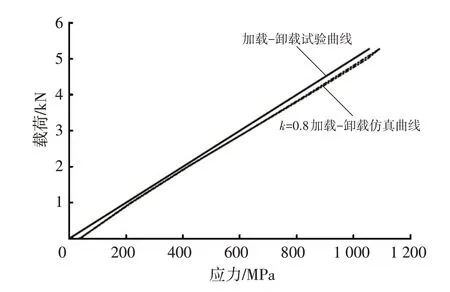
图7 板簧根部应力对比

加载至最大载荷时，仿真板簧2的应力与试验结果的相对偏差为3.38%，通过上述分析，证明了该模型是准确可靠的。

4 叶片曲率对少片变截面钢板弹簧力学特性的影响

以3种不同结构参数的少片变截面钢板弹簧为例，其中少片簧1为斜线型钢板弹簧，少片簧2与少片簧3为抛物线型主副钢板弹簧，利用所建立的建模方法搭建不同曲率的少片簧仿真模型，为方便探究曲率的影响，设叶片向上弯曲时曲率k>0，叶片向下弯曲时曲率k<0，叶片平直，即不考虑曲率时k=0，曲率的正负仅表示叶片弯曲方向，曲率大小以|k|表示。对于曲率k≠0的主副簧复合式钢板弹簧，以其副簧端点与首片主簧上表面对应点间距离为主副簧间隙。进行叶片曲率对少片簧力学特性的影响规律的分析，少片簧结构参数如表4所示。

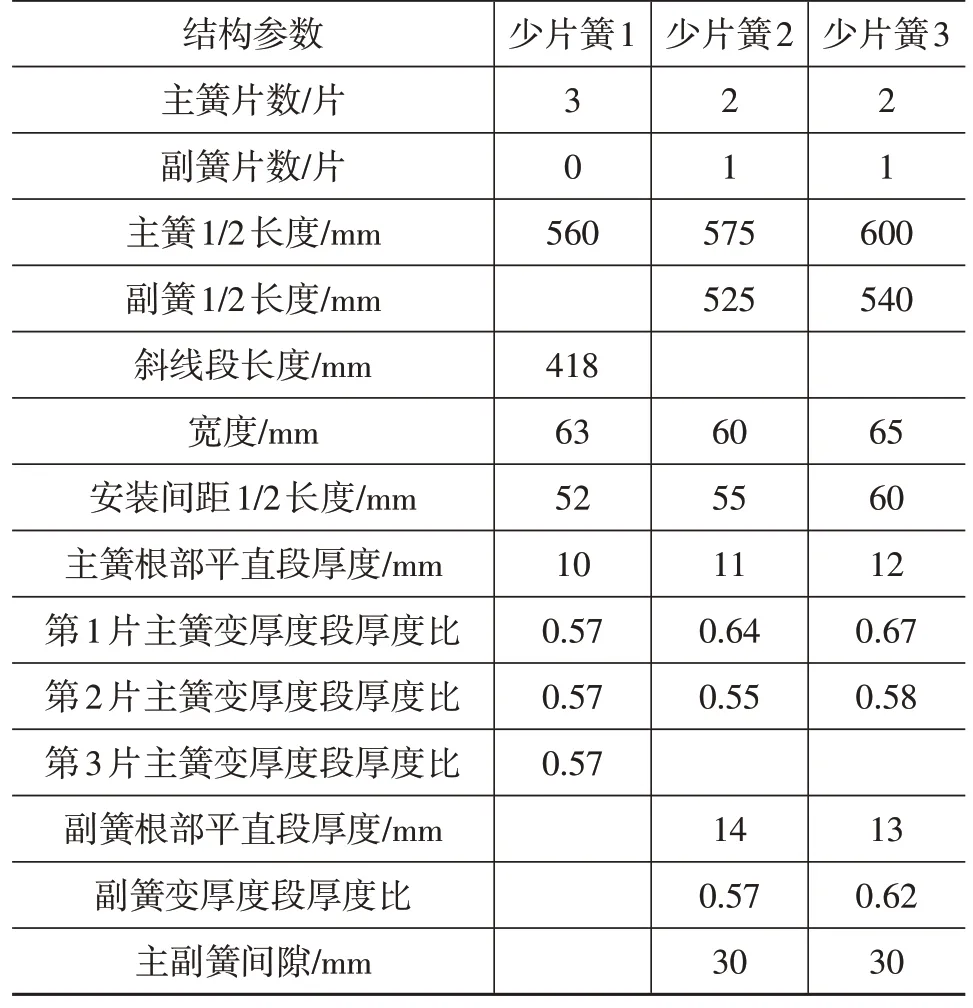
表4 少片簧结构参数

4.1 叶片曲率对刚度特性的影响

图8所示为仿真得到的叶片曲率对表4所示少片变截面钢板弹簧刚度特性影响的曲线。

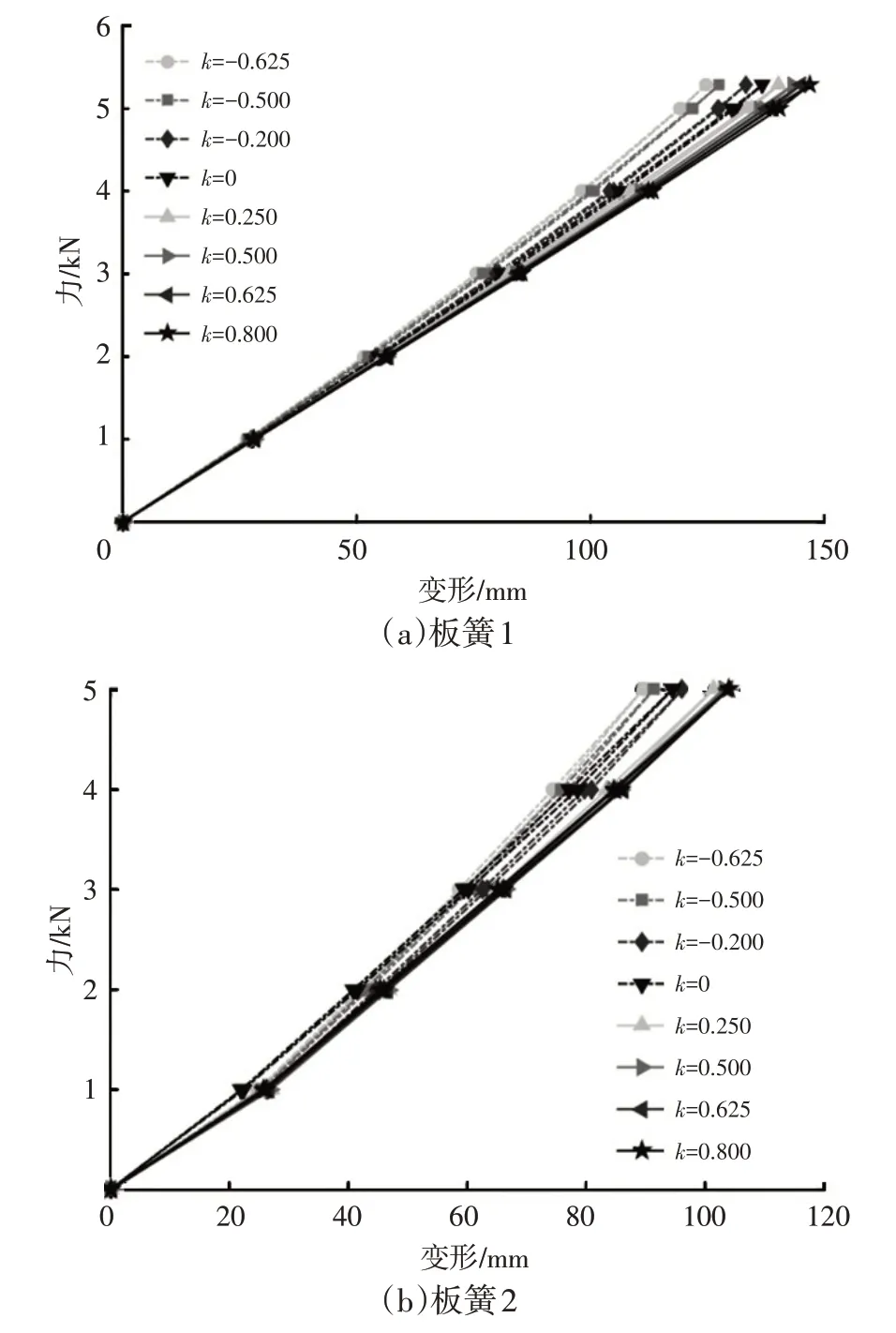
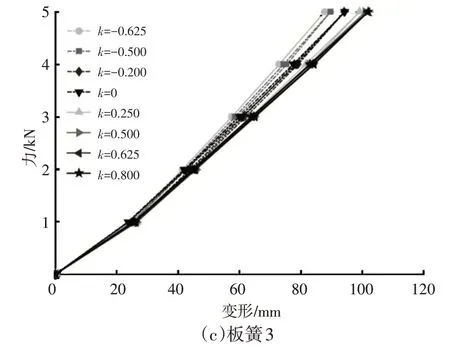
图8 刚度特性结果对比

由图8a可以看出：k<0时，相同端部作用力下，随着|k|的增大，板簧的变形减小；当曲率k≥0时，相同端部作用力下，随着|k|的增加，板簧的变形增加，但增加程度较曲率k<0时小。由图8b、图8c可以看出：k<0时，相同端部作用力下，随着曲率的增大，板簧的变形减小；当k>0时，随着曲率的增加，板簧的变形增加；板簧2 与板簧3是主副簧复合式钢板弹簧，k=0时，主副簧间隙一定，无法等同于其他曲率板簧的主副簧间隙，逐级加载时，其副簧早于其他非零曲率副簧进入接触，所以一定载荷范围内，其刚度较大，变形较小。

为了进一步分析叶片曲率对刚度特性的影响，图9给出了仿真所得的叶片曲率对表4 所示少片变截面钢板弹簧刚度影响的曲线，其中板簧1的刚度为加载至最大力下的刚度，板簧2与板簧3的刚度为主副簧完全接触后的复合刚度。

图9 不同曲率下的少片簧刚度

由图9 可以看出：叶片向下弯曲时，随着曲率的增大，少片簧的刚度增大，且增大趋势明显；叶片向上弯曲时，随着曲率的增大，少片簧刚度逐渐减小，减小趋势较为平缓。整体看来，图中曲线近似二次曲线。出现上述情况的原因可能是：叶片曲率变化导致端部作用力的作用线与板簧中心垂线的水平距离发生变化，从而导致了弯矩、片间接触摩擦的变化，且叶片向上弯曲时，施加载荷有使叶片曲率减小的趋势，叶片向下弯曲时，施加载荷有使叶片曲率增大的趋势。这种减小或增大趋势减缓或加剧了上述变化的程度，这种变化反映在刚度上使刚度曲线在不同曲率下近似呈二次曲线变化。通常，在板簧初始状态下，叶片呈现向上弯曲的形状。仿真结果显示，随着叶片曲率的增大，板簧抵抗弹性变形的能力降低，在悬架垂直载荷一定时，刚度减小导致悬架垂直变形增大，增加了撞击限位块的概率。对于主副簧复合式钢板弹簧，刚度降低会造成副簧过早进入接触状态，导致板簧不能满足实际工作要求。

为了进一步分析叶片曲率对刚度的影响程度，表5给出了仿真所得的不同非零曲率下的少片簧刚度对于不考虑曲率时的变化量。从表5中可以看出，随着曲率的增大，变化量逐渐增大，即曲率对刚度的影响程度逐渐增大。通常，少片簧初始状态下的曲率在0.5～0.8 m-1范围内，为了便于工程应用，同时简化求解过程，可以在不考虑板簧曲率进行计算分析的基础上，以曲率-刚度修正系数γ进行修正，γ的取值范围为0.06～0.08。

表5 刚度变化量

4.2 叶片曲率对应力特性的影响

图10 给出了仿真所得的叶片曲率对表4 所示少片变截面钢板弹簧的第2 片主簧同一节线距离板簧端部不同位置处的应力曲线。

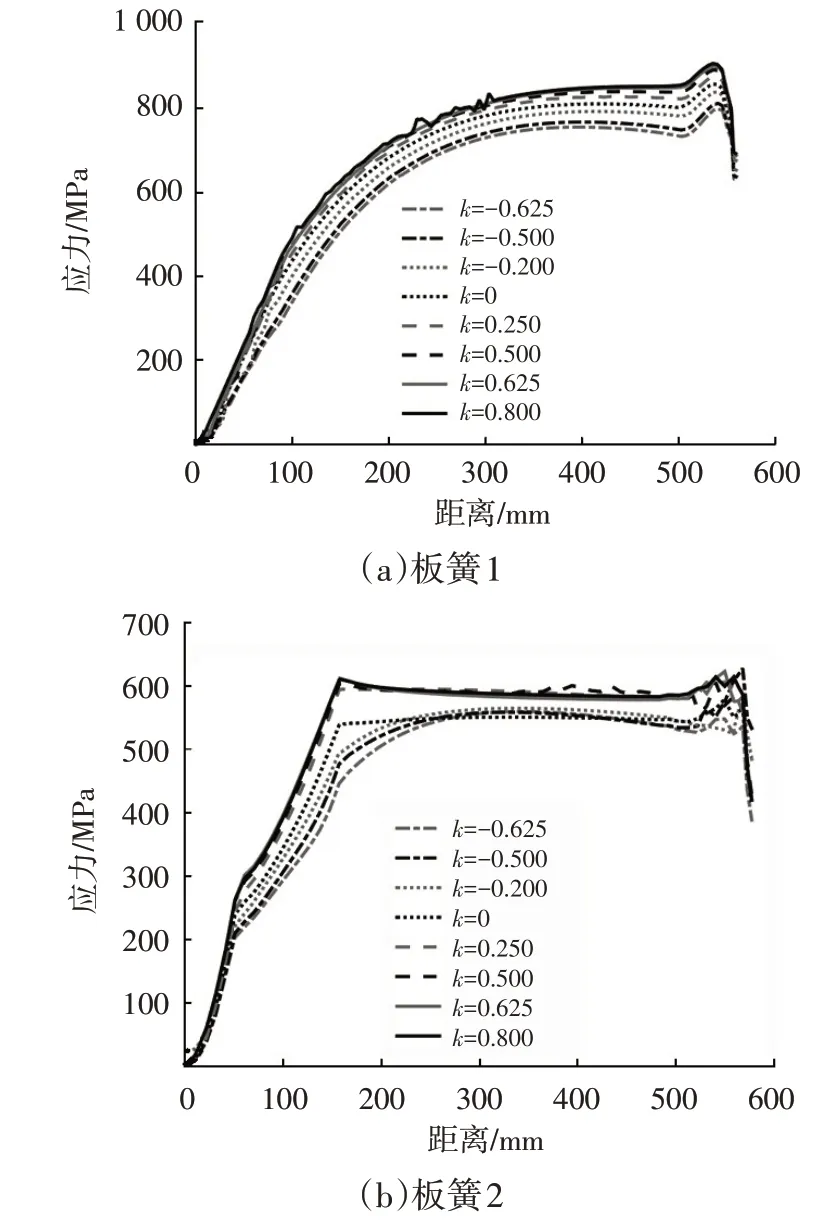
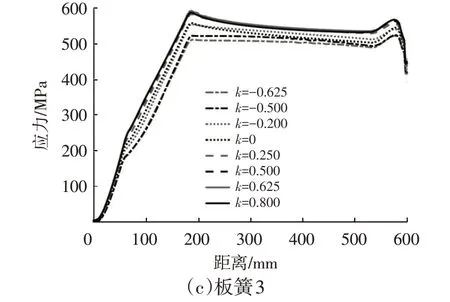
图10 板簧不同位置处的应力曲线

由图10a 可以看出：当k=0 时，在端部力的作用下，板簧1 某一节线上的应力由端部平直段到变厚度段迅速增加，而后增加趋势趋于平缓，并在根部平直段出现最大应力；当板簧1 的叶片曲率改变时，同一节线上的应力整体变化趋势与曲率k=0时一致，曲率的存在并没有改变板簧1的应力分布，仅改变了应力的大小。由图10b 可以看出：当k=0 时，在端部力的作用下，板簧2 某一节线上的应力先是沿长度方向迅速增加，而后在抛物线段出现等应力现象，最后在根部平直段出现最大应力；当板簧2 的叶片曲率改变时，同一节线上的应力分布发生了变化，如曲率k>0 时，在主簧对应副簧端点位置处出现了较大的应力。由图10c可以看出：当k=0时，在端部力的作用下，应力由端部平直段到变厚度段迅速增加，在主簧对应副簧端点位置处出现了较大的应力，下降后趋于不变，而后又再增加并在板簧根部平直段出现了应力最大值；当板簧3的k<0时，随着曲率的增大，主簧对应副簧端点位置处的应力逐渐减小，在此位置不再出现较大的应力分布。整体来看，当板簧长度、厚度不变时，曲率的存在可能会改变其应力的大小或分布情况。

为了进一步分析叶片曲率对应力特性的影响，图11 给出了仿真所得的叶片曲率对表4 所示少片变截面钢板弹簧的根部最大应力影响的曲线。

图11 不同曲率下的少片簧根部最大应力

由图11可以看出，在叶片曲率的影响下，少片簧的应力呈非线性变化。k>0 时，应力随曲率增加而增加，k<0时，应力随曲率的增加而减小。出现上述情况的原因可能是：叶片曲率变化导致端部作用力的作用线与板簧中心垂线的水平距离发生变化，从而导致了弯矩、片间接触摩擦的变化，这种变化反映在应力上使应力曲线在不同曲率下呈非线性。图11 中板簧2 与板簧3 的应力曲线在k=0 处出现尖点的原因是：板簧2 与板簧3 是主副簧复合式钢板弹簧，k=0时，主副簧间隙一定，无法等同于其他曲率的板簧。

为了进一步分析曲率对应力的影响程度，表6给出了仿真所得的不同非零曲率下的少片簧应力对于不考虑曲率时的变化量。从表6中可以看出，随着曲率的增大，变化量逐渐增大，即曲率对应力的影响程度逐渐增大。为了便于工程应用同时简化求解过程，可以在不考虑板簧曲率进行计算分析的基础上，以曲率-应力修正系数λ进行修正，λ的取值范围为0.02～0.04。

表6 应力变化量

5 结束语

本文通过考虑曲率对少片变截面钢板弹簧的影响，建立了其上、下表面曲线的构造方法，并利用台架试验验证了该方法的正确性；通过有限元分析，对不同曲率的少片簧的力学特性进行了探究，得到以下结论：

a.少片变截面钢板弹簧刚度及应力随叶片曲率变化的一般规律为：叶片向上弯曲时，随着曲率的增大，少片簧的刚度逐渐减小，应力逐渐增大；叶片向下弯曲时，随着曲率的增大，少片簧的刚度逐渐增大，应力逐渐减小。

b.为了便于工程应用，同时简化求解过程，可以以曲率-刚度修正系数γ与曲率-应力修正系数λ对不考虑叶片曲率的板簧模型的刚度和应力进行修正，从而提高设计精度，优化板簧设计，延长板簧寿命，保证少片簧更好地满足实际工作要求。