基于深度卷积-长短期记忆神经网络的整车道路载荷预测
罗欢 胡浩炬 余家皓
(广州汽车集团股份有限公司汽车工程研究院,广州 511434)
1 前言
在现有的汽车底盘结构疲劳耐久分析流程中,为了获得整车的道路载荷谱,通常需要在项目开发早期开展整车道路耐久试验,该试验需要特制的试制样车、测量设备、试验场所以及数周的试验时间。随着控制成本和缩减开发周期的要求日益严格,道路试验成本高、周期长的问题更加突出,亟待解决。
近年来,针对如何在取消道路试验的条件下获得底盘结构疲劳耐久分析所需的道路载荷问题,国内外的学者主要提出了2类分析技术:基于整车动力学分析的虚拟路谱技术和基于机器学习的路谱识别技术。前者首先通过激光扫描技术获取试验场路面不平度信号,然后对包括轮胎、衬套悬置等弹性元件的整车模型进行动力学仿真分析[1-4];后者首先利用合适的机器学习模型直接根据方便测量的整车参数预测道路载荷,然后利用整车动力学仿真分析获取底盘结构件的动态响应载荷[5-8]。通过对比这2种方法,发现与虚拟路谱技术相比,基于机器学习的路谱识别技术省去了操作复杂且代价高昂的路面不平度测量工作,且不需要在整车动力学模型中建立轮胎模型。
尽管相关研究越来越多,目前基于机器学习的路谱识别技术仍然存在2个方面的问题:相关研究涉及的工况比较简单,没有充分覆盖当前道路试验通常包含的试验场路面;相关研究中利用的机器学习模型非常传统,如反向传播(Back Propagation,BP)、径向基函数(Radial Basis Function,RBF)、非线性自回归(Nonlinear Autoregressive Exogenous,NARX)等神经网络模型,这些神经网络模型所能达到的预测精度低于更为先进的深度学习模型[9-12]。因此,整车路谱的识别作为典型的非线性时序数据预测问题,更适合采用深度学习神经网络模型。
本文针对上述问题,基于整车试验场测量数据,探索了利用深度神经网络模型建立整车结构参数和运行参数与道路载荷之间的关系,建立了包括试验数据预处理、整车参数选择、神经网络模型训练和测试的完整流程,以期为进一步实现利用数据库和深度学习预测道路载荷提供理论基础。
2 DCNN-LSTM模型及其设计
在基于机器学习的路谱识别技术研究中,为了根据整车运行参数有效地预测以轮心六分力为代表的路谱载荷,需要从众多可实际测量的整车结构参数和运行参数中挑选出与轮心六分力最相关的部分,并建立合适的机器学习模型,从大量的样本数据中确定挑选的整车运行参数与轮心六分力之间的对应关系。
深度学习模型作为机器学习领域的最新研究成果,在处理高度非线性、高度动态特性问题时具有强大的学习能力,因此在大规模时间序列数据预测研究中得到广泛应用[9,11]。在众多的深度学习模型中,大量的研究证明,使用联合了深度卷积神经网络(Deep Convolutional Neural Network,DCNN)模型和长短期记忆(Long-Short Term Memory,LSTM)神经网络模型的DCNN-LSTM 模型可取得相对较高的预测精度[12-15]。
为了根据大量具有高度动态特性的整车运行参数预测对应的轮心六分力载荷,本文提出了基于DCNN-LSTM模型的整车路谱识别技术,其基本框架如图1所示。
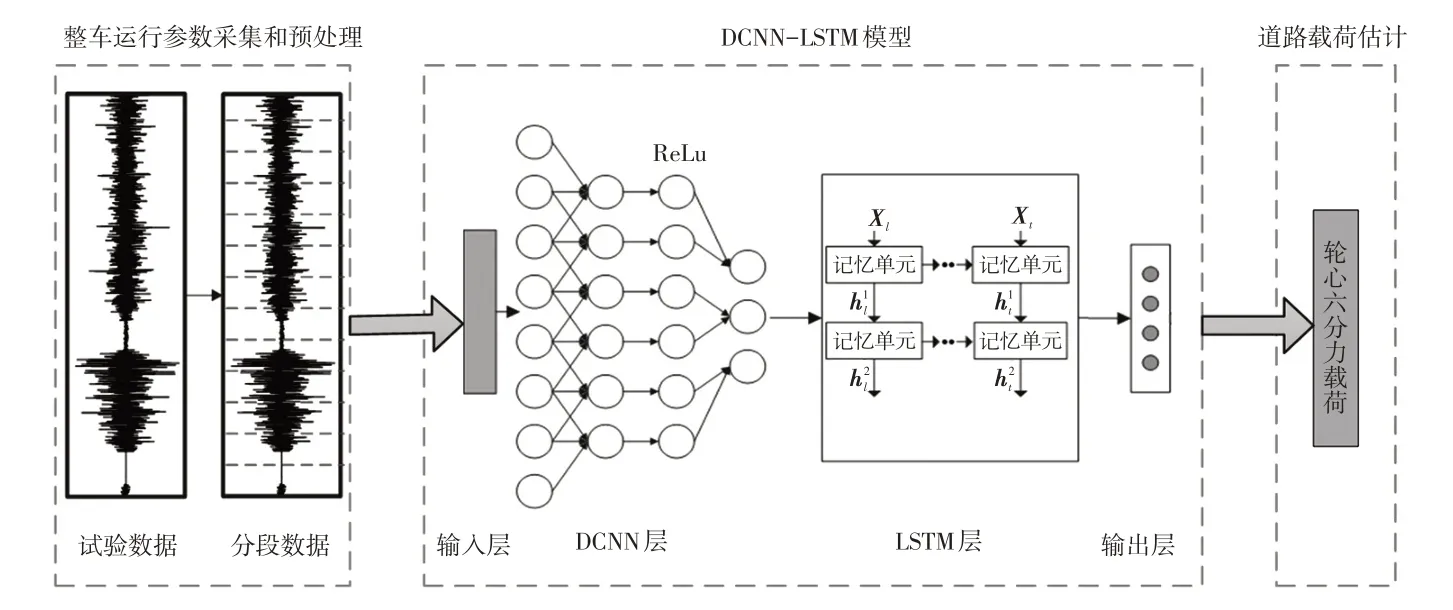
图1 基于DCNN-LSTM模型的整车路谱识别技术
2.1 DCNN-LSTM模型
DCNN-LSTM 模型主要包括输入层、DCNN 层、LSTM层以及输出层。其首先利用DCNN层提取输入层数据的重要特征信息,然后通过LSTM层及最后的全连接层预测轮心六分力载荷[13-15]。
DCNN 层通常由2 类交替连接的子层组成,即卷积层和池化层。在卷积层输入数据与卷积核进行卷积运算和求和运算,然后通过非线性转换获得卷积层的输出信息。在池化层,输入的数据被分为很多小块,通过对每小块求取统计值(如均值或最大值)即可得到池化层的输出信息。在整车道路载荷预测中,需要处理的汽车运行参数属于一维时序数据,因此DCNN 层选用如图2所示的一维卷积神经网络层。
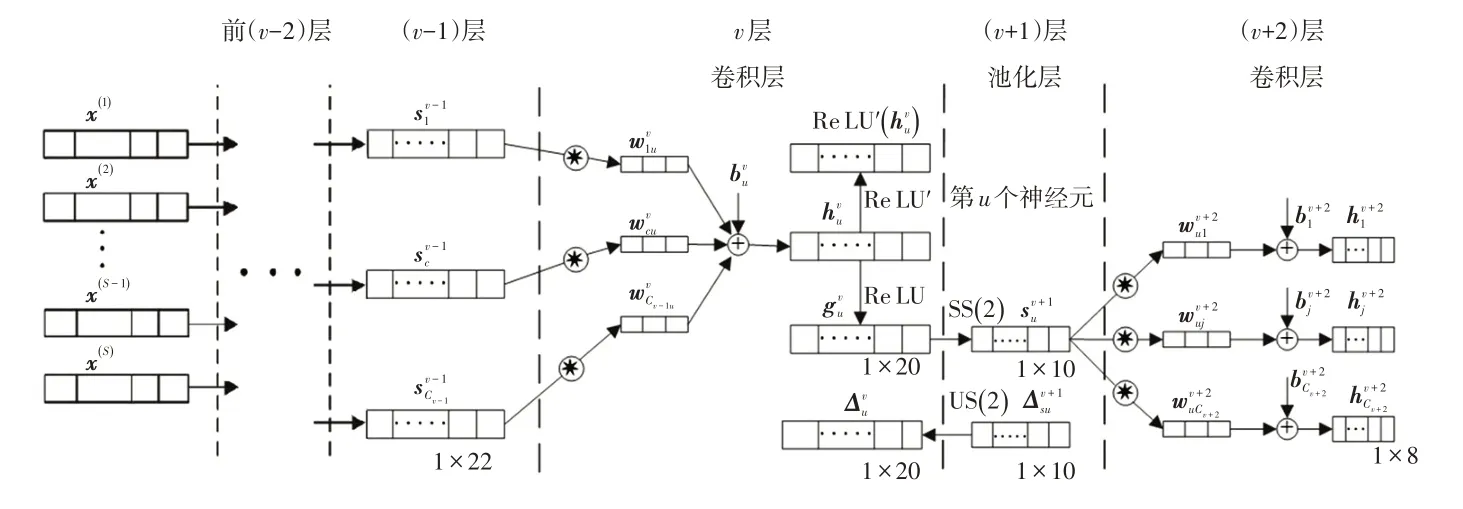
图2 一维卷积神经网络层
设输入层数据为xD=[x(1),…,x(S)],其中S为选择的整车运行参数的数量。在第v层(卷积层)中,一维卷积操作可表达为:
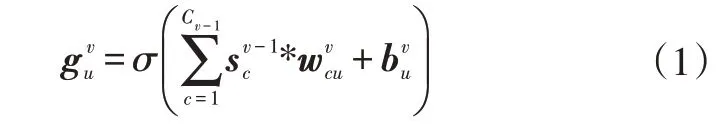
式中,为第v层的第u个数据;为第(v-1)层的第c个数据;表示由计算的卷积核权值参数,卷积核的数量对应于第v层输出数据的数量;为第v层的第u个偏置参数;Cv-1为第(v-1)层数据的总数量;*表示卷积运算;σ为非线性传递函数,在卷积神经网络模型中常用的非线性传递函数为线性整流单元函数(Rectified Linear Unit,ReLU),即σ(z)=max(0,z)。
池化层的计算过程可表达为:
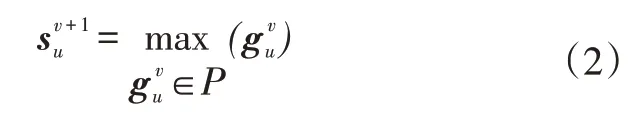
式中,为第(v+1)层的第u个数据;P为降采样的区域,设该区域的尺寸为1×M,移动步径为M,则通过降采样操作,数据的尺寸将变为原来的1/M。
如图3 所示,LSTM 层利用特殊的隐含层神经元(称为记忆单元)处理时间序列数据,每个记忆单元包括3 个主要元素,即输入门、遗忘门和输出门。LSTM层通过这3 个门单元控制信息的传递并且记忆信息中的时序状态。设Xt为LSTM 层的输入数据,Yt为与输入信息对应的LSTM 层输出数据,Ct为记忆单元的状态值,ht为记忆单元的输出值,在每个时间步t,记忆单元的各个门、状态值及隐含层输出值的计算过程为:
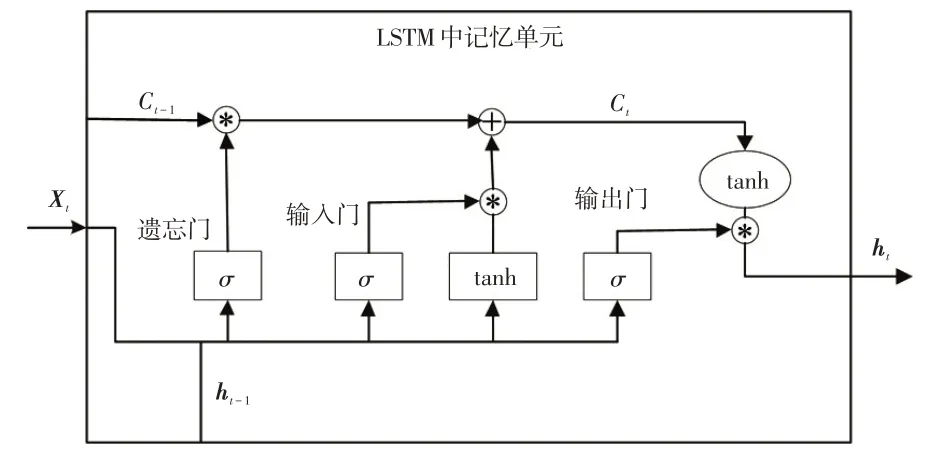
图3 LSTM层
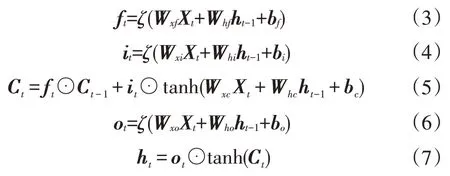
式中,⊙表示点积运算;ζ为非线性激活函数(通常为Sigmoid 函数);ft、it、ot分别为遗忘门、输入门和输出门;ht、Ct分别为t时间步的状态值和隐含层输出值;Wxf、Whf、Wxi、Whi、Wxc、Whc、Wxo、Who分别为遗忘门、输入门、状态值、输出门对应的权值向量;bf、bi、bc、bo分别为遗忘门、输入门、状态值、输出门对应的偏置向量。
如图1 所示的DCNN-LSTM 模型中,输出层为全连接层,在该层计算轮心六分力载荷Yt:

式中,Why和by分别为全连接层对应的权值向量和偏置向量。
2.2 整车参数选择
在整车道路载荷预测中,DCNN-LSTM 模型的输入是整车结构参数和运行参数。考虑到能够测量的整车结构参数和运行参数数量较多且每个参数的规模也较为庞大,直接将采集的所有整车运行参数作为DCNNLSTM模型的输入会导致模型本身比较复杂且影响计算效率[16]。为了避免此问题,同时保证模型的预测精度,需要对采集的整车运行参数进行选择。
在工程实际中,特征选择法可以从原始测量参数集中抽取对预测值具有最重要贡献的参数子集。该方法由于分别计算了各候选参数对预测值的影响,故可以有效地对所有候选参数的重要性进行排序[17]。在众多的特征选择方法中,综合考虑各候选特征参数的相关性、冗余性以及互补性的基于冗余-互补散度的数据驱动特征选择(Redundancy-Complementariness Dispersionbased Feature Selection,RCDFS)方法,相比其他特征选择方法在预测精度和计算效率方面都表现更优[18]。为了挑选出对轮心六分力载荷影响最大的整车运行参数,本文利用RCDFS方法计算各测量参数对轮心载荷变化的贡献度,并基于贡献度排序确定最终挑选出的整车运行参数。
为了处理输入参数中的时域相关性,DCNN-LSTM模型要求每个输入样本为具有一定长度的时序信号,因此选择的整车运行参数在输入到DCNN-LSTM 模型前需要进行分段处理。本文参考其他学者的研究工作,将选择的整车运行参数试验数据均分为包括50个时间步长度的输入样本[19]。
2.3 DCNN-LSTM模型结构设计及评估
合理地设计DCNN-LSTM 模型的结构参数是保证取得较高预测精度的关键。在模型设计过程中,需要确定的结构参数主要包括:DCNN层中卷积层和池化层的数量、各卷积层的神经元数量、卷积核的尺寸、LSTM 层的数量和各LSTM层的神经元数量、全连接层的数量和各全连接层的神经元数量。为了评价具有不同结构参数的DCNN-LSTM模型能够取得的预测精度,选择均方误差EMSE和相关系数R2作为评价指标:
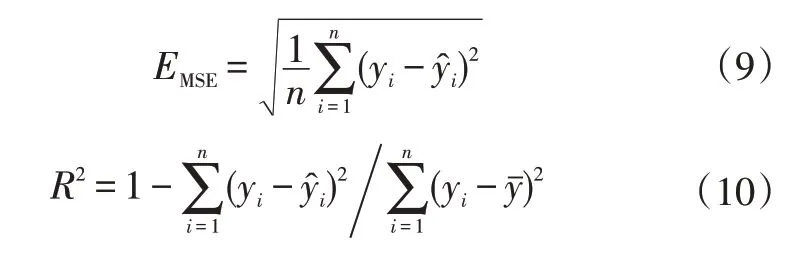
式中,yi、分别为目标值和预测值;为目标值的平均值;n为样本数量。
EMSE可反映预测值的稳定性,其值越小,表示预测值的精度越高。R2可表示预测值与目标值变化趋势的一致性,其取值范围为0~1,数值越接近1,表示预测值与目标值的相关性越强。
本文在对具有不同结构参数的DCNN-LSTM 模型进行训练时,利用EMSE评价训练过程中每次迭代获得的预测值。预测值的EMSE通过反向传递的方式从最后的输出层逐步向前传递到第1 个卷积层。预测误差反向传递的过程中,权值的更新采用最常见的随机梯度下降法。对训练完毕的各DCNN-LSTM 模型,同时采用EMSE/ERMS和R2评价其预测值的精度,其中均方根ERMS为:
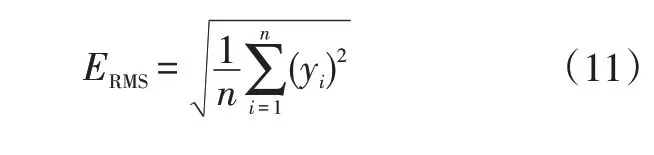
3 基于DCNN-LSTM 模型的轮心六分力载荷预测
基于某些样车在襄阳试验场进行道路耐久试验采集的数据,建立合适的DCNN-LSTM 模型,在多种运行工况下进行轮心六分力载荷预测。
3.1 试验数据采集
收集多款车型在整车道路耐久试验中采集的测试数据,各车型试验过程的整备质量和后悬架形式如表1所示。
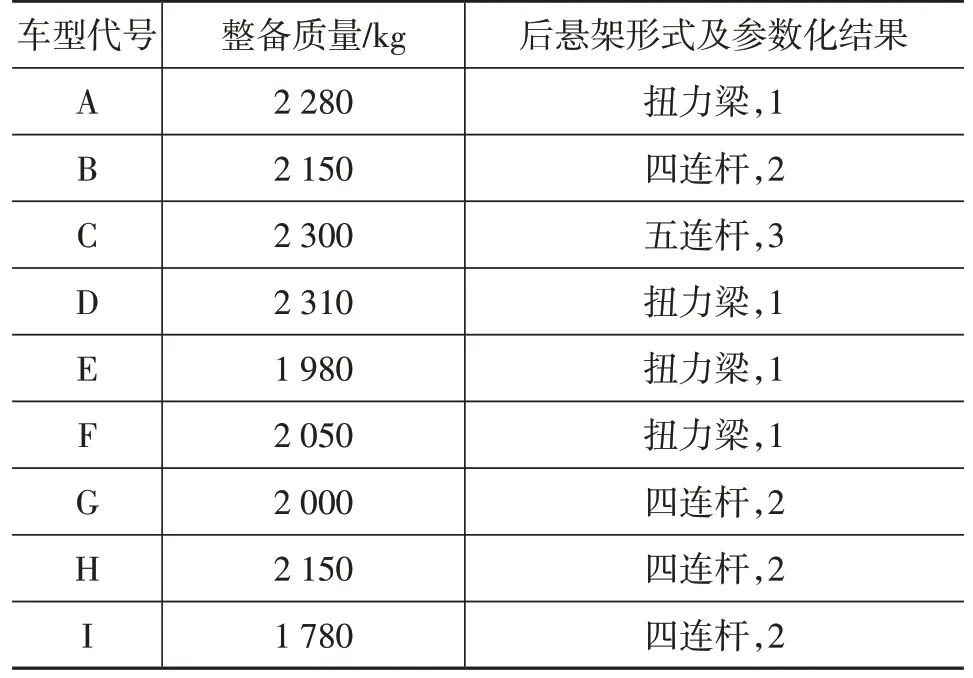
表1 各车型的整备质量及后悬架形式
整车道路耐久试验在襄阳试验场进行,该试验场具有多种典型的耐久试验路面,包括凸块路、搓板路、制动路、坑洼路、卵石路、石块路、砂石路、共振路等。整车在试验场行驶过程中,装备有多种传感器,包括轮心六分力传感器、加速度传感器、惯性导航仪、应变传感器等。通过这些传感器以及整车内置传感器,测量了多种整车运行参数,包括车速、转向盘转角、整车质心加速度等。
3.2 DCNN-LSTM模型参数选择
为了确定DCNN-LSTM模型的输入参数,首先利用RCDFS方法分析测量的整车运行参数对轮心载荷变化的贡献度。该分析基于某车型的测量数据进行,并参考路面形式将轮心载荷进行分类[20]。分析结果表明,对轮心载荷影响最重要的几项整车运行参数依次为转向盘转角、质心纵向加速度和车速。此外,考虑到不同车型的整车质量、悬架形式以及耐久试验的路面形式与轮心载荷也具有很强的相关性,共选择了6 项参数作为DCNN-LSTM 模型的输入:传感器测量的转向盘转角、质心纵向加速度以及车速,参数化的整车质量、悬架形式以及耐久试验的路面形式。
为了设计合适的DCNN-LSTM模型,在模型设计阶段,首先将每种路面下的试验数据进行归一化处理,然后随机分为训练样本数据、校核样本数据和测试样本数据。其中训练样本数据和校核样本数据用于更新每个DCNN-LSTM 模型的权值向量,测试样本数据用于评价每个DCNN-LSTM模型的预测精度。理论上,增加深度学习模型的层数有利于提高其预测精度,然而,层数过多会引起2个严重问题:增加计算负担,降低计算效率;导致模型参数过多,增加模型设计难度。为了确定合适的结构参数,参照其他的研究案例[21-23],将DCNN-LSTM模型的重要结构参数限定在一定的范围:卷积层的数量限定为1~5 层,各卷积层神经元的数量限定为10~500个;池化层的数量限定为1~5 层;LSTM 层的数量限定为1~3 层,各LSTM 层神经元数量限定为10~500 个;全连接层的数量限定为1~3 层,各全连接层神经元数量限定为10~200 个。通过比较不同模型的测试精度,确定最优模型的结构参数为:C(128)-C(128)-C(128)-P(2)-C(256)-P(2)-C(256)-P(2)-L(400)-F(200)-F(200),其 中C(nc)表示神经元数量为nc的卷积层,P(M)表示池化区域尺寸为M的池化层,L(nl)表示神经元数量为nl的LSTM层,F(nf)表示含有nf个神经元的全连接层。
3.3 轮心六分力载荷预测
利用DCNN-LSTM 模型预测了多款车型在不同试验场路面下的轮心六分力载荷,并与试验测量值进行对比,结果如图4 所示。在不同试验场路面下,特别是当整车运行于低频试验路面时,预测的轮心垂向载荷
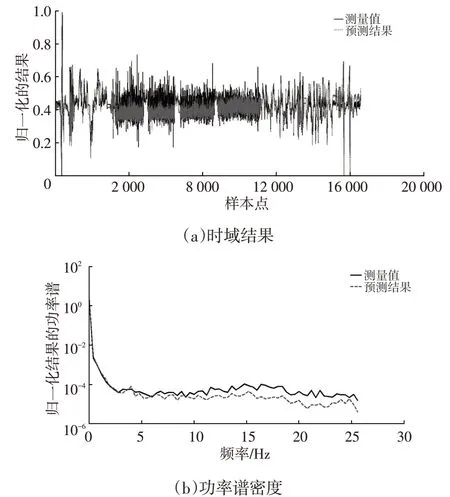
图4 轮心六分力载荷预测值与测量值对比结果
与试验测量结果在时域变化、功率谱密度分布方面均比较一致。某款车型不同轮心力载荷的预测值与试验测量值之间的EMSE/ERMS和R2如表2 所示,由表2 可知,EMSE占ERMS的比例在0.05~0.2 范围内,R2在0.5~0.8 范围内。预测的不同轮心六分力载荷伪损伤与试验测量值处于相同量级,如图5 所示,这进一步表明预测的轮心力载荷与试验测量值比较接近,能够满足结构疲劳耐久分析的要求。表2 和图5 中,Flfx、Flfy、Flfz、Frfx、Frfy、Frfz、Flrx、Flry、Flrz、Frrx、Frry、Frrz分别为左前轮心纵向、侧向、垂向载荷、右前轮心纵向、侧向、垂向载荷、左后轮心纵向、侧向、垂向、右后轮心纵向、侧向、垂向载荷。
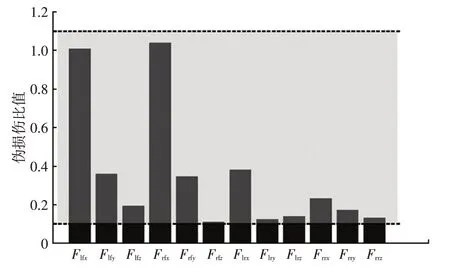
图5 某车型不同轮心力载荷的伪损伤比值
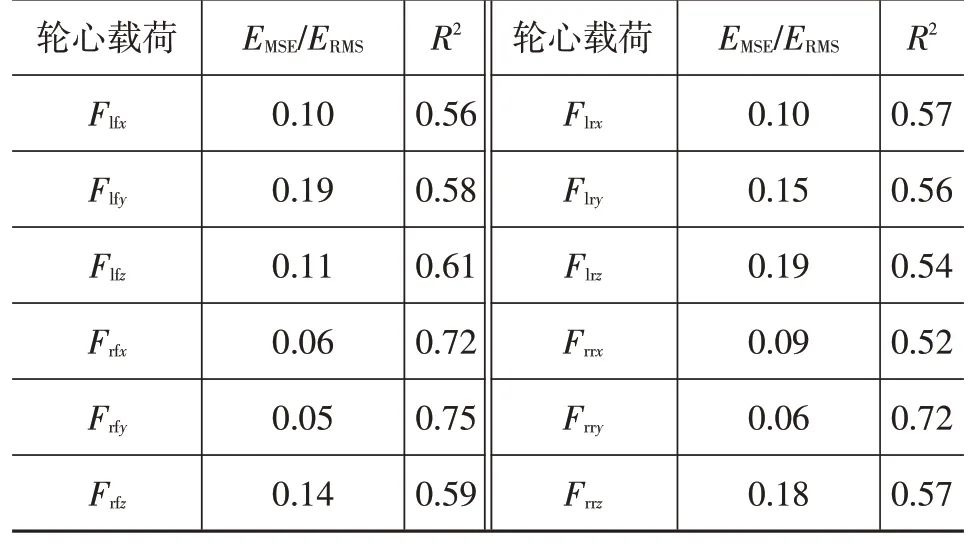
表2 某车型轮心力载荷的预测精度
基于DCNN-LSTM 模型轮心力载荷预测值与试验测量值在时域、频域、伪损伤方面均比较接近,这证明了基于现有数据库进行轮心载荷预测具有较强的可行性。应用该预测方法能够减少汽车底盘结构疲劳耐久分析对整车道路耐久试验的依赖,并可以有效降低分析成本、提高分析效率。
4 结束语
本文从实际应用角度出发,利用多款车型在试验场道路试验中测量的数据,研究了基于DCNN-LSTM模型的整车道路载荷预测,解决了试验数据预处理、整车运行参数选择、DCNN-LSTM 模型结构参数确定等问题,提出了将实际可测量且具有明确试验规范的参数作为输入,利用合适的DCNN-LSTM模型预测不同路面下轮心六分力载荷,并确定了合适的评价指标。
将利用DCNN-LSTM 模型预测的轮心六分力与实际测量值进行了多方面比较,分析结果表明,两者不仅在时域和频域范围内均比较接近,而且预测值的伪损伤误差也很小,这证实了基于数据库和深度学习神经网络进行道路载荷预测可获得较高的精确度。在后续研究中,为了持续推进在底盘结构耐久设计阶段逐步减少甚至取消整车道路试验,将针对高频试验路面下数据动态特性更强、非线性关系更复杂导致的精度相对偏低问题,继续优化DCNN-LSTM模型的各项参数或者采用其他深度学习模型,进一步提高轮心六分力载荷预测精度。

