知识+方法+思想

陆芳芳

【摘 要】以加法、减法概念为核心的加法结构包含多种数学概念，如总数、部分数、差数、大数、小数等，一般分为变化题、合并题和比较题，学生若一直停留在题文推理的解题水平，则不利于加法结构的完善。教师应通过将数学方法和数学思想融合于数学知识的概念教学中，助力学生达到概念推理的解题水平，为数学课程的学习打下良好基础。

【关键词】知识 方法 思想 概念

日本数学家米山国藏说：“作为知识的数学出校门不到两年就忘了，唯有深深铭记在头脑中的数学的精神、思想、研究的方法和着眼点等，这些随时随地地发生作用，使人终身受益。”方法、思想形成的基础和载体是知识技能，因而方法和思想的习得需扎根于知识技能的学习过程中。同时，只有在知识技能的学习过程中将方法和思想相融合，学生才能在火热的思考中感受到冰冷的美丽。

人们获得的数学知识，多是在以概念（词）为节点的语义网络中储存的，人们头脑中的概念有个重要的特征，即它们都是被嵌入到一个有组织的概念体系中。因而，教师应把数学基本概念的教学置于重要地位。加法和减法是数学课程的基础，以加法、减法概念为核心的加法结构又包含多种数学概念，如总数、部分数、差数等。在纷繁复杂的加减法实际问题中，如何帮助学生做到举一反三和触类旁通呢？本文就从三个维度谈一谈“知识+方法+思想”的教学模式在加减法实际问题教学中的运用。

一、知识维度——掌握核心概念，生成“一”

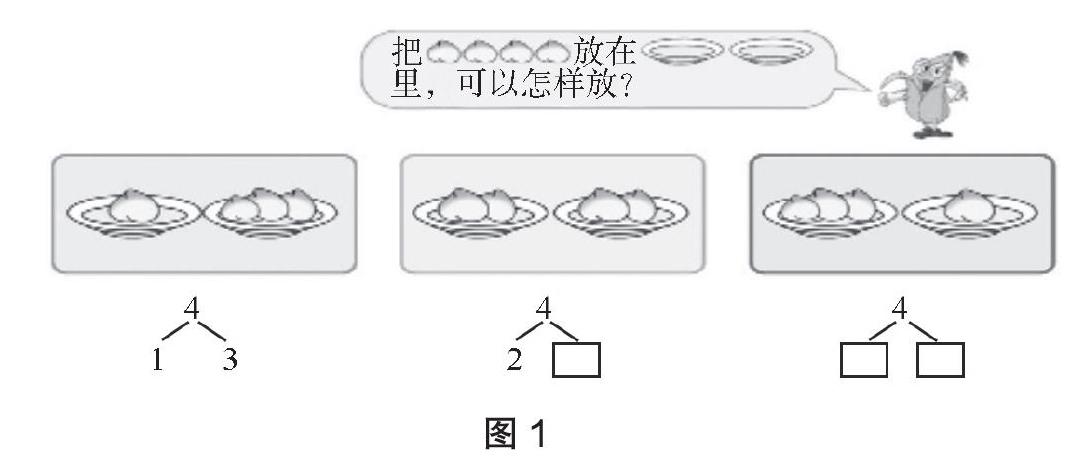
教材将“分与合”单元编排在认识加减法之前，除了将“分与合”作为加减法的口算方法基础，同时也作为加减法的概念铺垫。教师容易忽略“分与合”这一基本算术技能在加减法概念发展中的重要作用。通过“分与合”的教学，教师在帮助学生体会“分与合”的有序性之外，还应让学生初步感受部分与总体的关系，即将一个总体分成两个部分，以及两个部分合成一个总体（见图1）。

孙昌识教授将加减法实际问题分为三大类：变化题、合并题和比较题。其中，学生以生活经验为基础形成了加减法的概念雏形，如数量增加用加法，数量减少用减法。教材在编排上也遵循学生的认知规律，先认识变化题（题文中有暗示增量或减量的动词，如“又来了”“走掉了”等），顺势引导学生利用已有生活经验初步建构加减法概念，即合并图式;再认识合并题（题文中没有暗示增量或减量的动词，三个量是包含关系），进一步丰富学生的加减法概念，知道两个部分数合起来是总数用加法，从总数中去掉一个部分数得到另一个部分数用减法，即部分与总体关系推理图式;随着解题经验的积累，教师应引导学生将原有以生活经验为主导的合并图式整合到部分与总体关系推理图式中，逐渐摆脱生活经验的束缚，学会用概念进行思维，逐渐接近加减法概念的本质。

在变化题的教学中，笔者也遇到了一些顽固性问题，如：划走6只船后，还剩5只船，原来有几只船？不少学生列式为“11-6=5（只）”，因为数字较小，他们在列式之前已经知道了答案，但到了高年级，涉及的数字较大时，这种数字推理方式就行不通了。如何帮助学生走出困境呢？笔者认为，一些学生习惯了“减量用减法”的思维方式，新知与原有的认知产生了矛盾，教师应通过概念分析帮助学生将新知与原有认知加以整合：题目中虽然出现了减量动词，但是要结合加减法概念思考三个量的关系——“原来的只数”分成了“划走的6只”和“剩下的5只”这两部分，求总数只要把两个部分的数合起来，所以用加法。

在加减法实际问题的教学中，教师应引导学生从题文（找增、减量动词）驱动的解题方式向概念（推理部分与总体关系）驱动的解题方式转变，只有把握了概念本质，才能“一”以贯之，以不变应万变。

二、方法维度——联通核心概念，合成“类”

在三类加减法实际问题中，变化题和合并题便于学生建立部分与总体的关系图式，进而建构加减法概念，比较题涉及差数概念，不利于学生整合到部分与总体关系推理模式中，因而教材将比较题教学置后编排。新授课教学中，一些教师先告诉学生“比某某多用加法，比某某少用减法”，再运用此技巧进行练习，这属于题文驱动的解題方式，新授课采取此种教学方式实属不当。

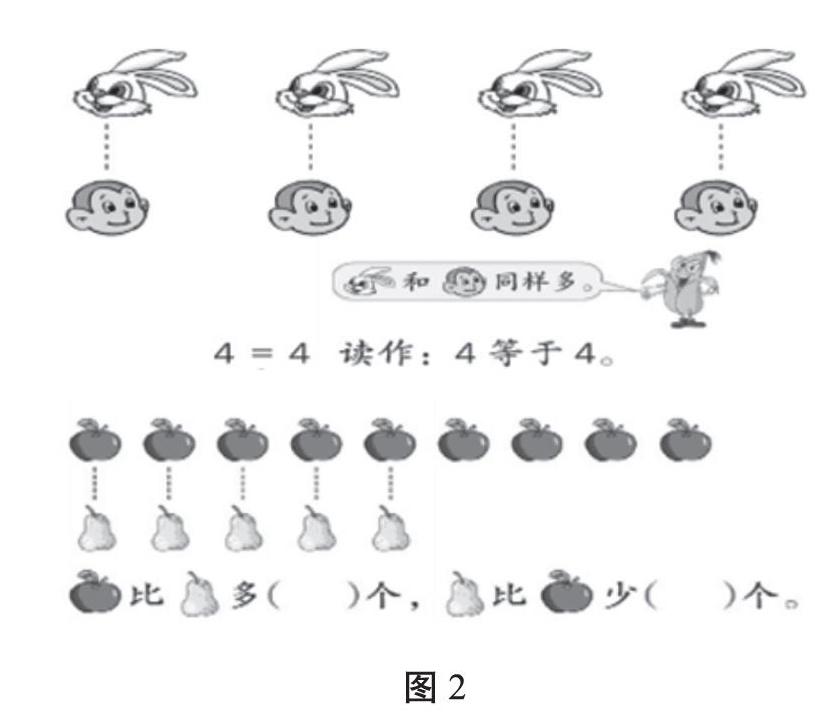
比较题中关于差数这一难点知识该如何处理呢？笔者认为，教师应当研读教材，从学生初次接触比较两个数量的多少开始，教材就引导学生一个对应一个地排（见图2），这对我们的教学也有所启示，即重视动作、线段图等表象在理解概念中的作用。

学生学习比较题的基础是“一样多”的概念和一一匹配的操作程序。学生能够通过一一匹配的直观图看出两个数量（大数、小数）相差多少，但如何用算式表征？如何沟通算式与减法概念的联系？这都需要借助动手操作和线段图等形象直观的教学方法。

比较题的教学编排分成两部分，一年级下册是“求两数相差多少的实际问题”，二年级上册是“求比一个数多（少）几是多少的实际问题”，在教学中，教师要重点引导学生联系加减法概念列出算式。

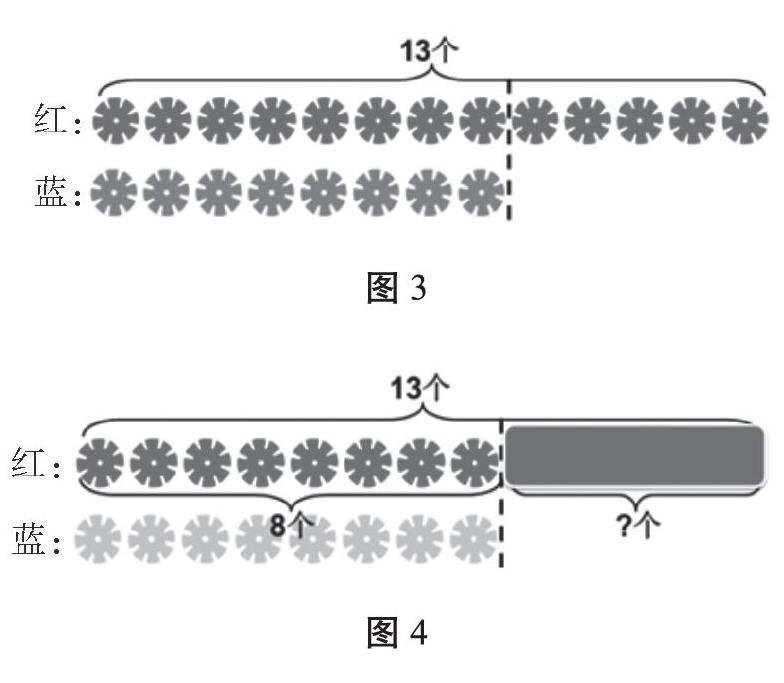
笔者在教学“求两数相差多少的实际问题”时，首先提出明确的操作要求：怎样摆，能让别人一眼看出来哪种花片多？多几个？在学生操作、展示的基础上，课件显示（见图3），明确 “红花片多，多5个”;课件显示（见图4），将蓝花片设置成透明效果，引导学生联系直观图理解算式，13个红花片分成了两部分，一部分是与蓝花片同样多的8个，另一部分是多出来的个数，从总数中去掉与蓝花片同样多的8个，就是多出来的个数，即13-8=5（个）。

“求比一个数多（少）几是多少的实际问题”的教学可作类似处理。将大数（总体）、小数（一部分）、差数（另一部分）通过直观的方法整合到部分与总体关系的推理图式中。这样，学生就能将求大数与求总数归为同一类问题，将求小数、求差数与求部分数归为同一类问题，即合成“类”。

三、思想维度——融合核心概念，达成“通”

加法结构是一个概念域，是以加法减法概念为核心的概念体系，是多种数学概念（部分数、总数、差数等）围绕加减法概念形成的联结网络。在加法结构的建构过程中，加法和减法也从分离状态逐渐实现整合——减法是加法的逆运算。

教材从“分与合”单元开始渗透分解与合成的互逆关系，在“一图四式”的教学中，要求学生看图写出四道算式（见图5），进而明确“同一幅图既可以看作是把总体分成两部分，也可以是把两部分合成总体”。“求未知加数”的教学，在尊重学生算法多样化的基础上，要相机介绍用减法求未知加数（见图6）。以上内容都是学生在直观感知的基础上，初步感受到加法、减法之间的联系。

一年级下册“20以内的退位减法”的教学，教师要在倡导算法多样化的基础上优化算法，以引导学生在逻辑抽象层面进一步理解加法、减法之间的联系（见图7）。

笔者在学习评价中采取以下检测方法，能有效甄别学生解决加减法实际问题时采取的解题方式，同时通过适当的训练，帮助学生理解题目中三量之间的关系，以提高学生概念驱动的解题水平。先提供一组文字描述的题目，如：①小丽和小军共有20枚邮票，小丽有8枚，小军有几枚？②妈妈买来一些蘋果，吃了6个后，还剩5个，妈妈买了多少个苹果？③一分钟跳绳比赛中，小红跳了82下，小军比小红多跳4下，小军跳了多少下？④张阿姨已经做了40件上衣和28条裤子，至少再做多少条裤子就能和上衣配套？⑤一分钟跳绳比赛中，小红跳了82下，小明比小红少跳6下，小明跳了多少下？再出示线段图（见图8），要求学生根据题文信息选择匹配的线段图，并将条件填在合适位置，再列式解答。

教师在具体操作中，也可根据学生情况调整实际问题的难易程度。在这个过程中，学生首先要将问题中的条件抽象成总数、部分数、大数、小数和差数等概念，多个问题可以用同一幅图表征，这时线段图作为模型就能帮助学生通过部分和总体关系推理出数量关系，进而列出正确算式。在整个过程中，三个基本数学思想——抽象、推理和模型得以渗透，打破了加法、减法彼此孤立的状态，达成“通”，并进一步完善了学生的加法结构。

钱阳辉老师说：“知识背后没有方法，知识就不可能被调用，只能成为一种僵硬的学问与沉重的负担;方法背后没有活生生的思想，方法也不可能被创造性地灵活运用，只能是一种笨拙的工具。”知识技能是基础，数学思考、问题解决、情感态度的发展离不开知识技能的学习，知识技能的学习必须有利于其他三个目标的实现。因此，在知识技能的教学中，应注意数学方法的指导和数学思想的渗透，让数学学科核心素养得以真正达成。

综上所述，坚持采用“知识+方法+思想”的数学教学模式，我们的学生即使离开了校园，依然会用数学眼光观察世界、会用数学思维分析世界、会用数学语言表达世界，这也是我们致力追求的数学教育愿景。

【参考文献】

[1]孙昌识，姚平子.儿童数学认知结构的发展与教育[M].北京：人民教育出版社，2004.

[2]钱阳辉.发展学生思维的关键在于展开探索过程[J].江苏教育，2009（5）.

注：本文系无锡市陶行知研究会“十三五”课题“核心素养立意下的加减法实际问题大单元教学研究”（课题编号：XTD-025）的阶段性研究成果。