一种基于偏振度估计的自适应导航方法*
张 原 邢 琰 熊 凯
北京控制工程研究所,北京 100094
0 引 言
太阳光在穿过地球大气层时会发生散射现象,形成大气偏振光。包括砂蚁和蜜蜂在内的许多动物都能利用大气偏振光获取方向信息,进行导航[1]。
基于偏振光的定向方法具有抗干扰性强,自身无源等优点,是一种完全自主的导航方式[1-4]。将偏振光与SINS、GPS等进行组合可以有效提高系统导航精度。同时,基于偏振光的导航方式还具备测量误差不随时间累积发散、敏感器体积小的优点,具有广泛的应用价值。
现有的应用偏振光导航的方法中,大多通过偏振光敏感器的输出解算偏振方向角,然后利用偏振方向角进行导航[1-5]。虽然有误差补偿与标定的过程[6-7],但是让偏振光敏感器的测量独立于导航系统的其他部分,其测量误差仍会一直存在于此后的导航运算中。光电式偏振光敏感器依据其测量原理,其误差参数对于输出结果的计算有相当的影响,尤其是偏振度的解算受影响极大。实际应用中,偏振度虽然不直接用于导航,却与偏振光敏感器测量精度直接相关。事实上,当偏振度低到一定程度(通常认为小于0.05)时,偏振光敏感器输出的信噪比会变得极低,此时其测量结果将不再可信[1]。然而现有的偏振光导航方法中,很少考虑到偏振度[1-5]。
针对现有的偏振光导航方法对于偏振度的重视不足,为了能够准确地获得偏振度,本文提出了一种应用于最大偏振度的“当前”统计模型估计方法,同时应用于导航中。“当前”统计模型是我国学者周宏仁在singer模型的基础上,假设当前的加速度为瑞利分布提出的一种加速度预测模型[8]。自提出以后,许多学者都进行了相关的研究,其应用十分广泛[9-11]。该方法借鉴机动目标跟踪中的加速度“当前”统计模型的思想,根据最大偏振度本身的物理特性,假设被测量天空区域当前的最大偏振度为修正的瑞利分布,提出了均值自适应模型。仿真结果表明,该方法能够在载体运动中准确地跟踪最大偏振度的变化。
1 大气偏振模式
太阳光在大气中传输时,被大气层中的空气分子、气溶胶粒子散射,大气散射辐射具有偏振特性。在晴朗无云的条件下,大气对于太阳光的散射主要是瑞利散射,散射后的光线主要是线偏振光,线偏振光以偏振度和偏振化方向来描述[1]。
偏振化方向为偏振光最大偏振度的方向,偏振方向同观测点位置的太阳矢量方向垂直。偏振度P由散射角θ决定,散射角为散射后的光线传播方向与原传播方向的夹角
(1)
其中Pmax表示最大偏振度,理想天气情况下Pmax=1。
太阳和天顶的连线称为太阳子午线。根据瑞利散射理论,大气偏振模式关于太阳子午线与太阳矢量所在的平面呈对称分布[1],如图1所示,图中虚线表示偏振方向。

图1 大气偏振模式示意图
2 偏振光测量
2.1 偏振光敏感器工作原理
偏振光敏感器的结构如图2所示,主要结构一对偏振敏感单元和一个对数减法器。偏振敏感单元由色彩滤光片、偏振片和光电转换元件组成[2]。

图2 敏感器结构示意图
两个偏振敏感单元的偏振片的极化方向相互垂直,天空偏振光经过敏感单元后两路信号经过对数减法器形成敏感器输出。其输出为
(2)
其中P表示偏振度,φ表示太阳光最大偏振方向与第一敏感单元中偏振片极化方向的夹角。通常情况下,偏振光敏感器设置为三组,偏振片极化方向依次增加π/3,考虑到元器件参数、安装等带来的误差,综合各种误差因素后实际的输出为
(3)
其中Δfpi(i=1,2,3)表示是加性误差,Δki(i=1,2,3)表示乘性误差,Wfpi(i=1,2,3)表示测量噪声,为0均值白噪声。其中各路敏感器的Δki(i=1,2,3)不同所导致计算时的误差影响最大。
偏振光敏感器误差系数的来源通常是元器件参数不一致以及安装误差等导致的,一般通过标定获得,不考虑标定残差认为是固定的常数[5-6]。
2.2 偏振光敏感器输入角与航向
所使用的坐标系定义如下:
载体坐标系(简称b系):载体坐标系固联在载体上,坐标原点在载体的质心,x轴沿载体横轴指向右,y轴沿载体纵轴指向前,z轴垂直x-y平面,并沿载体的竖轴指向上。
导航坐标系(简称n系):以载体质心为坐标原点,x轴正方向指向东,y轴正方向指向北,z轴正方向指向天顶向上。
敏感器坐标系(简称m系):以偏振光敏感器参考方向为x轴,在不考虑安装误差的情况下相当于等于b系绕z轴转-90°,对应旋转矩阵为
(4)
(5)

(6)
俯仰角和滚转角可以通过其他测量得到,因此式(6)可以看作偏振光敏感器输入角与载体航向间的关系式。
假设载体运动方向在水平面的投影与航向一致,以速度的方向表示载体运动方向,则有
(7)
其中ve表示东方向速度,vn表示北方向速度。
3 跟踪导航滤波器结构
3.1 最大偏振度的“当前”统计模型
“当前”统计模型是机动目标跟踪中常用的一种表征目标加速度统计特性的模型。目标以某一加速度机动时,“当前”统计模型认为机动加速度可能取值的范围可以缩小。因为当目标现时正以某一加速度进行机动时, 下一瞬时机动加速度的取值范围是有限的, 而且总是在“当前”加速度值附近。

针对最大偏振度的这一特性,可以参考加速度“当前”统计模型的思想,构建类似的最大偏振度“当前”统计模型。
加速度“当前”统计模型认为,由于物理上的限制, 目标现时加速度值越大, 在下一瞬时目标加速度大幅度偏离此值的概率就越小。因此采用修正的瑞利分布来描述加速度的统计特性。
参考加速度“当前”统计模型,最大偏振度的概率密度采用修正的瑞利分布来描述,当前最大偏振度预测值为最大偏振度均值。
(8)
其中μ为唯一待定参数,根据均值即为分布的期望可得到
(9)
其中E[Pmax]为最大偏振度均值,在每一个时刻μ有确定取值,各时刻不一定相同,相应的最大偏振度方差为
(10)
采用一阶时间相关模型来描述最大偏振度:
(11)


3.2 最大偏振度方差自适应导航算法
所研究的问题针对地表附近的情况,加速度的测量通过加速度计获得。选取导航滤波用的状态变量为
X=[δvTPmax(Δb)T]T
(12)
其中δv速度误差,Δb表示加速度计漂移矢量。
根据式(1),实时的最大偏振度Pmax可以通过偏振度P和散射角θ反向求取。太阳矢量的反方向即为太阳光原本的传播方向,视线方向的反方向即为散射后偏振光的传播方向,这两个方向的夹角即为散射角θ,有
(13)
θ不在滤波器中估计,作为一个参量处理。
根据捷联惯导速度误差方程,不考虑姿态误差,有
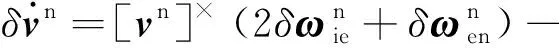
(14)

(15)
综合上述各式可以得到导航使用的状态方程

其中
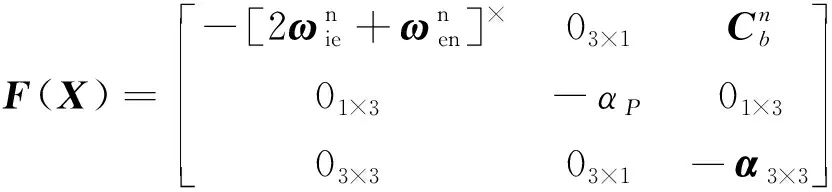
(16)
其中-α3×3=diag(-αbe,-αbn,-αbu),αbe,αbn,αbu分别为对应的时间常数的倒数,Wb为加速度计比力测量噪声。
对于式(3)而言,任意一路的偏振光测量模型均存在P和φ的取值不唯一却使得输出结果相同的情况,因此需要至少两个偏振光敏感器输出作为测量,以保证Pmax和ψ能够被估计。其中任意两组均可作为测量使用,这里选用前两组。
考虑速度误差的存在,式(7)可表示为
(17)

以加速度计输出为
(18)
其中[·]×表示对应的反对称矩阵,F表示加速度计输出矢量,a,g和v分别表示导航系下的加速度矢量、重力矢量和速度矢量,ωie表示地球自传角速度,ωen表示在地球表面附近移动因地球表面弯曲引起的导航系旋转角速度,WF表示加速度计测量噪声,为0均值白噪声。
偏振光敏感器输出取前两路
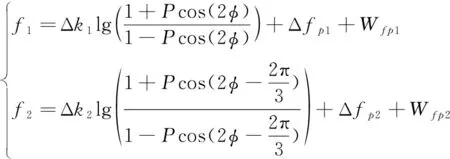
(19)
式(17)和(19)构成了偏振光敏感器与速度的内在联系。
考虑到式(3)中存在速度误差和速度保持同步变化的情况,这会使得含误差的速度方向与真实速度方向保持一致,此时仅依靠偏振光敏感器并不能对速度误差的估计有所帮助,因此需要引入新的测量,这里选取里程计作为新的测量工具。考虑到随运行时间增加,里程计输出数量级会远大于加速度计和偏振光敏感器,因此这里选取里程计输出的增量Δs作为测量值使用。有

(20)
其中Δt表示采样周期,Vs表示测量噪声。式(19)和式(20)联立则为量测方程,含有误差的速度通过加速度计解算得到。
4 仿真校验
仿真中设定载体运动轨迹为起始静止,以4m/s2加速度在30°角斜坡上运动,水平方向为北偏东33°,加速20s后开始匀速运动,斜坡匀速运动10s后转为平地匀速运动,50s后以4 m/s2减速运动10s,之后保持线速度不变以6(°)/s角速度向右旋转360°后结束。运动过程包括上坡、加减速和转向。
采样周期0.01s。初始时刻太阳方位角1.6902rad,太阳高度角0.1959rad,Pmax=0.4。地理位置东经E110°北纬N38°。偏振光敏感器的误差参数为Δk1=0.90, Δk2=1.05, Δfp1=0.010, Δfp2=0.012 偏振光敏感器测量噪声方差2.5×10-4, 误差条件下直接利用测量计算偏振光敏感器的输入角误差在0.12rad左右[11-12]。
Pmax按照如图3所示规律进行变化,其过程包括线性增加和减少以及按照三角函数波动变化。

图3 最大偏振度变化曲线
仿真结果如图4和图5所示。

图4 最大偏振度估计误差

图5 速度误差的估计误差
仿真结果显示,滤波后速度误差,最大偏振度和加速度计漂移均收敛。
1)载体姿态不变仅在加速和匀速之间转换时,估计误差变化较小,说明加速度的变化对估计结果影响较小;
2)载体转向时,航向角时刻在变化,使得偏振光敏感器输入时刻变化,反映到滤波结果中就是最大偏振度误差在产生小量波动;
3)最大偏振度估计发生波动时,速度误差估计真实值附近发生波动,这是由于偏振光敏感期中偏振度与偏振方向的耦合,导致了以偏振方向作为速度方向校正时估计误差随着偏振度产生波动,反映了偏振度变化对导航精度的影响。


图6 模型最大偏振度估计结果和估计误差

5 结论
“当前”统计模型作为机动目标跟踪中应用最广泛的模型,有其优越性。根据模型假设中的共通处,本文提出了一种最大偏振度的“当前”统计模型,并应用于导航中。利用偏振光敏感器输出和里程计增量输出为测量,以及偏振光敏感器输入角与航向之间的关系来同时估计加速度计速度误差和最大偏振度。相对于以往的偏振光导航方法,该方法直接使用偏振光敏感器的输出作为测量,取消了解算偏振方向角的过程,通过滤波器估计最大偏振度,将最大偏振度纳入了导航系统的考虑范围。数值仿真结果表明,该方法可以实现对于速度偏差信息和最大偏振度的估计,对于最大偏振度有良好的跟踪效果。

