高速再入飞行器分数阶PIλDμ稳定域分析
秦昌茂 王 兴 雷延花
中国运载火箭技术研究院,北京 100076
0 引言
高速飞行器再入过程中,由于马赫数高达10以上,飞行中气动参数受到马赫数及攻角变化的影响,导致高速飞行器是一类参数大范围快速时变、强非线性的复杂被控对象,传统PID控制往往难以获得满意的控制效果,而目前普遍应用的鲁棒控制、自适应控制及滑模控制等[1-5],虽然控制效果很好,但是增加了控制器设计的复杂程度,并且也没有对高速飞行器的稳定域进行相应的分析。
分数阶PIλDμ[6]将传统PID的整数阶次推广到分数阶次,由于比传统PID具有更强的鲁棒性及更好的控制效果[7-8]及继承了传统PID结构简单等特点,分数阶PIλDμ在其他领域已获得应用。分数阶PIλDμ控制器设计过程包括数字实现及参数整定2部分,目前数字实现方法[9-10]中以薛定宇的改进Oustaloup算法获得较好的近似效果。分数阶PIλDμ相较于传统PID增加了2个阶次参数,目前的参数整定主要是通过优化算法来确定,有极点配置法、频率法及遗传算法[11]。在分数阶PIλDμ的稳定域分析中,主要是使用D-分解法针对分数阶系统[12-13]或是参数不确定时滞系统[14]分析控制器参数稳定区域,但并未整定λ和μ两个参数。
本文基于最优Oustaloup数字实现及高速飞行器非线性俯仰通道模型建立仿真框图,结合ITAE指标利用遗传算法寻优整定分数阶PIλDμ参数,然后针对选定的分数阶PIλDμ控制器,利用D-分解法分析高速飞行器的马赫数及攻角稳定区域,以确定所设计的控制器稳定控制范围和控制参数,同时保证控制器具备最优的稳定性。最后结合跟踪微分器设计了改进的分数阶PIλDμ控制器。
1 分数阶PIλDμ最优Oustaloup数字实现
基于Oustaloup滤波器在(ωb,ωh)频率段内实现分数阶微分算子sμ的近似,在该滤波器之前增加一个滤波器来提高数字实现近似精度,将分数阶微积分sμ近似为:
sμ≈G×Gc
(1)
其中G为滤波器,Gc为Oustaloup滤波器。
滤波器G的形式为:
(2)
其中的参数通过最优算法寻优确定。为了提高频率段内幅频及相频近似精度,将分数阶微积分sα近似算法的幅频及相频与实际的幅频及相频之间的误差作为寻优性能指标,即:
(3)
其中,M1和P1代表实际的幅频及相频,M2和P2代表近似算法的幅频及相频,ρ为调整因子,可以调整幅频及相频近似的侧重。一般取ρ=0.5。通过寻优使得J达到最小来确定滤波器G的参数。
以分数阶算子s0.5为例,取频率段为[0.001,1000],N=4,以改进算法中的滤波器参数作为优化的初始值,经过寻优之后,得到最优参数为:
分别利用Oustaloup算法及最优Oustaloup算法进行仿真,频率响应曲线如图1所示。

图1 分数阶算子s0.5频率响应曲线
分数阶PIλDμ微积分阶次一般取λ,μ∈[0 ∶0.1 ∶1],最终设计的分数阶PIλDμ框图如图2所示。

图2 分数阶PIλDμ仿真图
2 分数阶PIλDμ参数整定
以高速飞行器俯仰通道为例,俯仰通道模型如下:

(4)
其中:
r=h+RE
CL=0.6203α
CM(α)=-0.035α2+0.036617α+5.3261×10-6
CM(δe)=ce(δe-α)
式中:V,θ,h,α和ωz分别表示飞行器的速度,弹道倾角,高度,攻角和俯仰角速度;L,Mz分别表示升力和俯仰力矩;m,Iz,μ,S和RE分别表示飞行器的质量、俯仰转动惯量、重力常数、参考气动面积和地球半径。其中飞行器仿真模型的参数见参考文献[1]。
遗传算法是一类借鉴生物界自然选择和生物遗传机制的随机化搜索方法,其主要特点是群体搜索策略和群体中个体之间的信息交换,优化搜索不依赖于梯度信息,尤其适合于处理传统搜索难以解决的复杂性和非线性问题。建立分数阶PIλDμ控制器及高速飞行器俯仰通道非线性模型,结合ITAE指标,利用遗传算法寻优整定分数阶PIλDμ参数,积分及微分阶次取μ,λ∈[0 ∶0.1 ∶1],参数Kp,Ki,Kd∈[1,100],高度h=30km,V=15,期望值α=10°,仿真结果如图3所示。

图3 不同λ和μ的ITAE值
从仿真结果可以看出,分数阶PIλDμ比传统PID可以获得更好的控制品质。
3 马赫数及攻角稳定域分析
将高速飞行器俯仰通道模型转化为非线性传递函数,被控系统模型为马赫数及攻角的函数。
(5)
其中:
A=s2+0.04078Vα2s-
0.001809Vαs+0.0013734Vs
B=-0.0015785V2α2+
0.0003344V2α+2.402×10-7V2
D=0.001317V2
选择分数阶PIλDμ控制器模型为:
C=Kp+Kis-λ+Kdsμ
因此,系统闭环传递函数为:
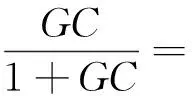
(6)
特征多项式为:
P(s;V,α)=
sλ(Aα+AC-B)+Dα·(Kdsλ+μ+Kpsλ+Ki)
(7)
定义1:设马赫数和攻角的稳定域为S,当K=(V,α)∈S时,控制系统稳定的条件是特征根均在s平面的左半部。
稳定域S由实部边界(Real region boundary,RRB),虚部边界(Imaginary region boundary,IRB)及复数边界(Complex region boundary,CRB)确定,3条边界线由D-分解法计算确定。边界由以下方程确定:
RRB:P(0;K)=0;IRB:P(∞;K)=0;
CRB:P(±jω;K)=0
将s=0代入到特征多项式中可得RRB边界线方程为:V=0。
由于高速飞行器俯仰通道传递函数分子分母最高阶次不相等,因此没有IRB边界线。
将s=jω代入特征多项式,可得CRB边界线方程。
复数的分数次方计算公式为:

其中,σ为实部,ω为虚部,γ为阶次。
利用上式可得:
将上式令特征多项式代入特征多项式,令实部及虚部都等于0,可得关于V与α的方程,其中ω∈(0,∞),所得数值解中取V>0,则稳定域边界为RRB在α=∞时与CRB相接,稳定区域为CRB边界曲线上方。
以分数阶PIλDμ控制器:
C=100(1+s-0.5+s0.9)
(8)
为例得到的方程如下所示:
0.06585V3α+0.014566V3αω1.4+
0.0011164V3α2ω0.5+0.092889V3αω0.5-
0.7071Vαω2.5+4.1393×10-5Vαω0.5-
0.000031426Vω0.5-1.2438×10-7V3ω0.5+
2.5087×10-5V3α3ω0.5-9.3312×10-4Vα2ω0.5=0
0.028836V2α3ω1.5+0.091979V3αω1.4+
0.0000331V2ω1.5-0.022882ω1.5-0.06585V3α-
0.0012791V2α2ω1.5+0.0015863V2αω1.5=0
(9)
解上述方程,即可得到V与α的稳定域边界。
3.1 λ对稳定域的影响
取μ=1,λ分别为0、0.2、0.4、0.6、0.8和1,得到高速飞行器V与α的稳定域如图4所示。

图4 λ变化时对稳定域的影响
从图中可知,随着λ的增大,稳定域不断减小,在攻角α∈[5°,15°]内变化很明显。传统PID的稳定域最小,而分数阶PIλDμ扩大了稳定域,说明分数阶PIλDμ比传统PID对系统参数的变化不敏感,且应用的范围更广,所以λ应取分数阶次并取较小值。
3.2 μ对稳定域的影响
取λ=1,μ分别为0.2、0.4、0.6、0.8、1,得到高速飞行器V与α的稳定域如图5所示。
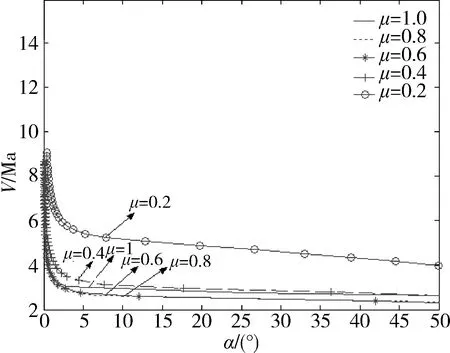
图5 μ变化时对稳定域的影响
从图中可知,随着μ的增大,稳定域先减小后增大,μ取较小值时,稳定域范围比传统PID小,当μ取0.6~0.8时,稳定域基本不变,比传统PID稳定域范围大,所以μ应取较大值。
4 改进的分数阶PIλDμ控制器
跟踪微分器(Tracking differentiator,TD)是自抗扰控制技术的重要组成部分,主要是解决在工程实际问题中,有效的给出不连续或有噪声的信号的跟踪信号和信号的微分。即跟踪微分器给出输入信号的跟踪信号以及跟踪信号的微分,用跟踪信号的微分来近似输入信号的微分。对于离散系统,具体算法如下[15]:

(10)
构造最速控制综合函数fhan(x1,x2,r,h),算法如下:

(11)
将u=fhan(x1,x2,r,h)带入系统中,以x1(k)-v(k)代替方程中的x1(k),就可以得到离散化的跟踪微分器:

(12)
其中,v(k)为输入信号,x1(k)为输入信号的跟踪信号,x2(k)为x1(k)的微分信号,可近似看为v(k)的微分信号,r为快速因子,r越大x1(k)跟踪v(k)也越快。h为滤波因子。
利用跟踪微分器改进分数阶PIλDμ控制器,将两者结合,为便于设计控制器,并结合前文的性能指标分析及分数阶次对稳定域的影响分析,选择分数阶次λ=0.2,μ=1。在稳定域满足实际应用的前提下,μ=1可以直接利用跟踪微分器输出的微分信号,如果μ≠1,可以直接加入分数阶PIλDμ微分对信号进行分数阶微分计算。
建立高速飞行器纵向通道非线性模型,构造如图6所示的高速飞行器俯仰通道自抗扰分数阶PIλDμ控制器:

图6 高速飞行器纵向通道控制框图
仿真参数选取如下:r0=300,h0=0.1,r1=300,T=0.001,其中,r0,h0分别为前向通路的快速因子和滤波因子,r1,h1为反馈通路的快速因子和滤波因子和T为采样时间,当V=15,期望输入α=10°,在输入信号中加入高斯白噪声及第5s时加入幅值10°的脉冲信号,仿真结果如图7所示。
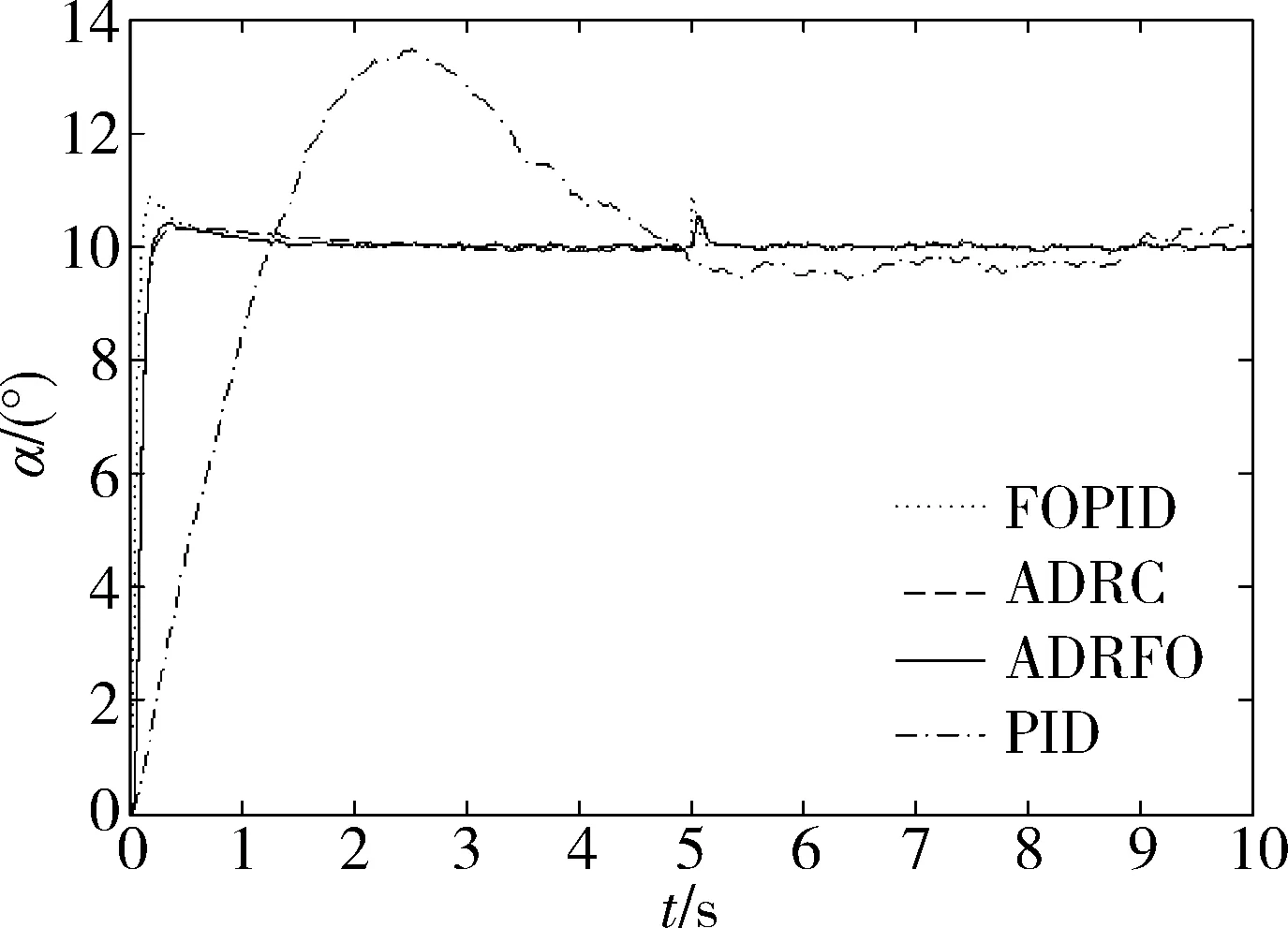
图7 控制器仿真结果
从图中可以看出,分数阶PIλDμ控制器上升时间短,响应快,能更好的满足高速飞行器的快速性要求,具有更高的稳定精度,能精确地跟踪控制指令达到期望值。而传统PIλDμ上升时间长,响应速度慢。
分数阶PIλDμ(FOPID)、自抗扰(Active disturbance rejection controller,ADRC)及自抗扰分数阶PIλDμ(Active disturbance rejection and Fractional-order PID,ADRFO)均比传统PID控制效果好,调节时间及超调量均优于传统PID,获得了更好的控制品质。而分数阶PIλDμ相比于自抗扰及自抗扰分数阶PIλDμ调节时间减少,但是超调量稍大,自抗扰超调最小,但是调节时间稍大,自抗扰分数阶PIλDμ介于两者之间。
从图7可知,当α=10°,V=2.7时,对于传统PID及自抗扰控制器而言,该系统是不稳定的。但是对于分数阶PIλDμ而言,该系统是稳定的,仿真结果如图8所示。
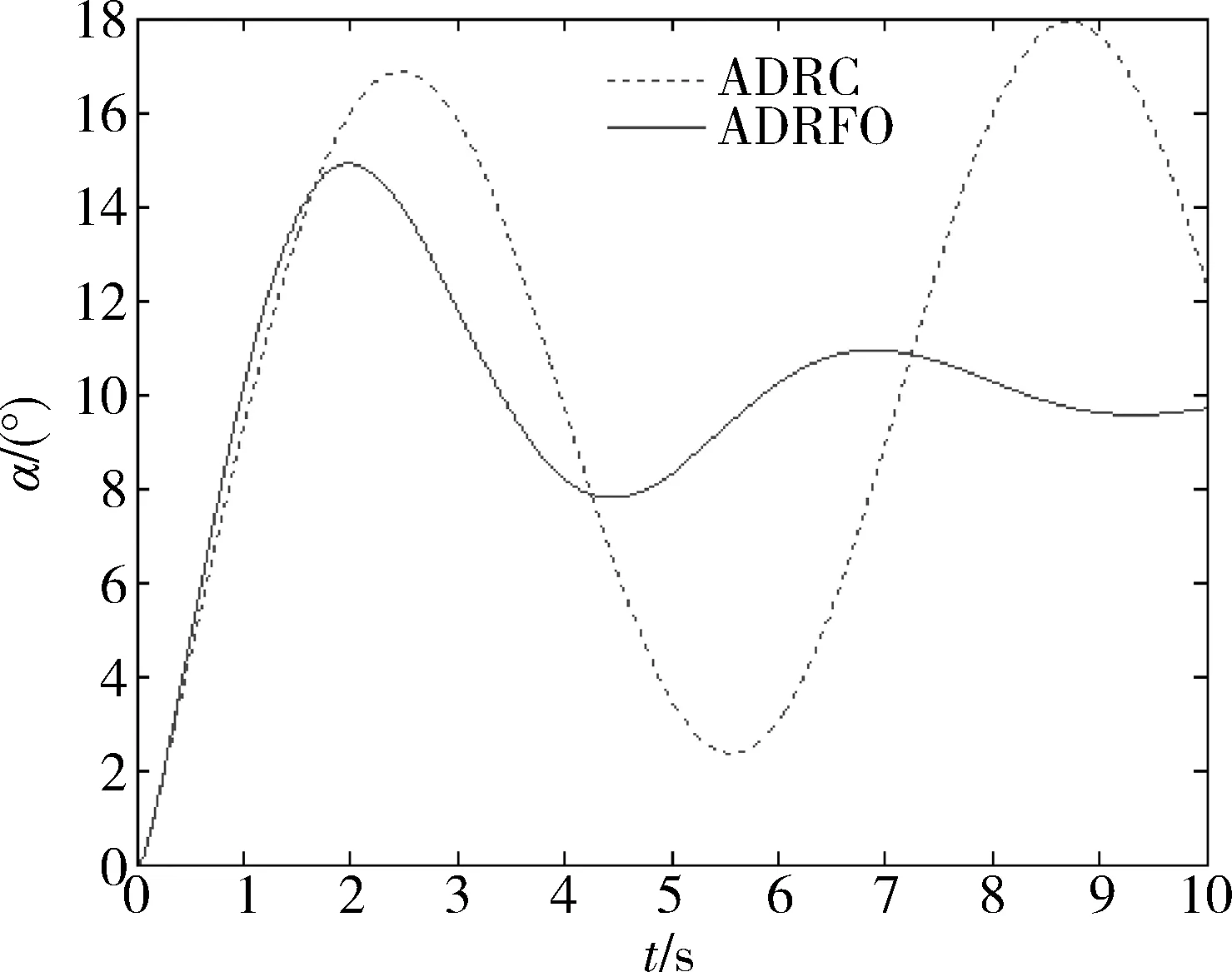
图8 控制系统稳定性分析
自抗扰控制仿真结果是发散、不稳定的,而自抗扰分数阶PIλDμ仿真结果是收敛、稳定的。由此,可以看出,自抗扰控制虽然设定了过渡过程时间,并且在超调量及调节时间方面有了很大改进,但是稳定域还是继承了传统PID的特点。而分数阶PIλDμ则扩展了传统PID的稳定域,提高了控制器的鲁棒性。因此结合自抗扰控制器及分数阶PIλDμ控制器的优点,在提高控制品质的同时,提高了被控系统的稳定域,也提高了控制器的鲁棒性。
5 结论
利用最优Oustaloup数字实现算法及遗传算法设计了高速飞行器的分数阶PIλDμ姿态控制器,并结合D-分解法计算出在确定的分数阶PIλDμ控制器下马赫数及攻角的稳定域。自抗扰分数阶PIλDμ通过跟踪微分器改进分数阶PIλDμ控制器,结合了自抗扰技术及分数阶PID控制器的优点,在噪声和大幅干扰存在的情况下,控制器仍然有较好的控制品质,且在解决快速性及超调量之间矛盾的同时,获得了较大的稳定域。仿真结果证明分数阶PIλDμ继承了传统PID结构简单等优点,获得更好的控制品质和更强的鲁棒性,满足高速飞行器快速性的要求,在马赫数及攻角大范围内变化的情况下也能保证控制品质及控制系统稳定。对于设计高速飞行器全程姿态控制系统,具有工程应用价值。

