基于启发式学习的折叠舵展开安全优化控制*

黄民昌 蒋 政 张 南 褚衍超 胡 勇

上海航天控制技术研究所，上海 201109

0 引言

舵机作为飞控系统的执行机构，其工作特性直接影响飞行控制的品质[1]。折叠舵(翼)以其结构简单、占用空间小、便于贮存、运输和发射等优点而广泛应用于导弹弹翼以及舵机机构[2]。导弹折叠舵的关键指标包括展开时间、展开冲击量级、可靠稳定性等。这些指标是导弹正常完成后续预定任务的前提，也对导弹传动机构、弹体框架等薄弱部位提出了耐冲击、高强度、高可靠的要求[3]。同时，以指标提升、持续学习为核心目标的航天智能控制系统也是今后的发展趋势[4]。

为了解决折叠舵展开时结构的冲击安全性问题，国内学者主要从以下两方面进行了较为充分的研究：一是对折叠舵展开冲击过程进行精细化分析，作为加强结构设计的指导与评估，如甄文强等对横向折叠翼展开过程进行考虑空气阻力和摩擦力矩的数学和动力学建模分析[5]。二是在结构设计上引入特殊设计方法，提高折叠舵本体抗冲击强度。如祝隆伟、张玉翠、刘芳等学者分别研究了间隙与折叠翼面振动的关系，各自提出了通过控制间隙从而减小碰撞力的方法[6-8]。李玉亮等在折叠舵中引入了减震垫，给出了力函数参数的确定方法[9]。

目前折叠舵展开冲击研究主要集中在抗冲击结构强度和振动两方面。而实际中却往往忽略了两方面重要问题，一方面，舵轴作为舵系统的传动件，在巨大的舵面展开冲击下，舵轴难以保持零位，如不进行适应性控制，容易激励出弹体的弹性振动[10]。另一方面，基于环境交互时冲击安全控制的思想，利用在短时间内舵轴旋转方向自由度的力和位移，可达到化解部分舵轴弯曲应力与舵面冲击应力的效果，避免传动件间的硬碰硬冲击。

因此，在舵面展开的瞬时过程中如何控制舵系统使得舵面的展开冲击最小成为一个最优控制问题。在最优控制问题的解决方法中，启发式策略以试探的方法，通过不断迭代生成较优解，以逼近最优解，具有良好的通用性和稳定性，广泛运用于仿生控制、人工智能、机器人等领域[11-14]。

本文针对舵面展开冲击过程舵系统安全最优控制问题，在引入舵系统自由度的基础上，分析折叠舵系统展开过程的动力学模型，建立了包含舵面展开运动耦合特性的控制系统模型。依据展开时间、最大舵轴弯矩、冲击残余动能三大指标作为约束条件，采用启发式学习的方法对舵面展开冲击过程中的舵系统优化控制进行迭代求解，经过仿真验证，经过优化后的舵系统展开过程达到了减少弯矩应力、减小冲击载荷的效果。

1 折叠舵展开多体动力学分析

1.1 折叠舵基本模型建立

某横向折叠舵分为2个部分，与舵轴固连的内舵，以及横向折叠的外舵，外舵初始与内外舵转轴折入一定角度，如图1所示。导弹发射后，燃气驱动外舵向外展开，在完全展开时刻锁紧销将内外舵锁制在一起[15]。

图1 某折叠舵结构示意图

如图2所示，针对舵展开原理建立固定坐标系OXYZ位于舵轴接口中心，δX、δY和δZ分别为沿各轴分量的单位基矢量，动坐标系pxyz与外舵固连，δx、δy和δz分别为沿各轴分量的单位基矢量，z轴与内外舵转轴重合，y轴垂直于外舵面，动坐标系qx′y′z′与内舵固连，δx′、δy′和δz′分别为沿各轴分量的单位基矢量，x′轴与内舵舵轴转轴重合，y′轴垂直于内舵面。令舵轴转角为θ，外舵展开角度为φ。

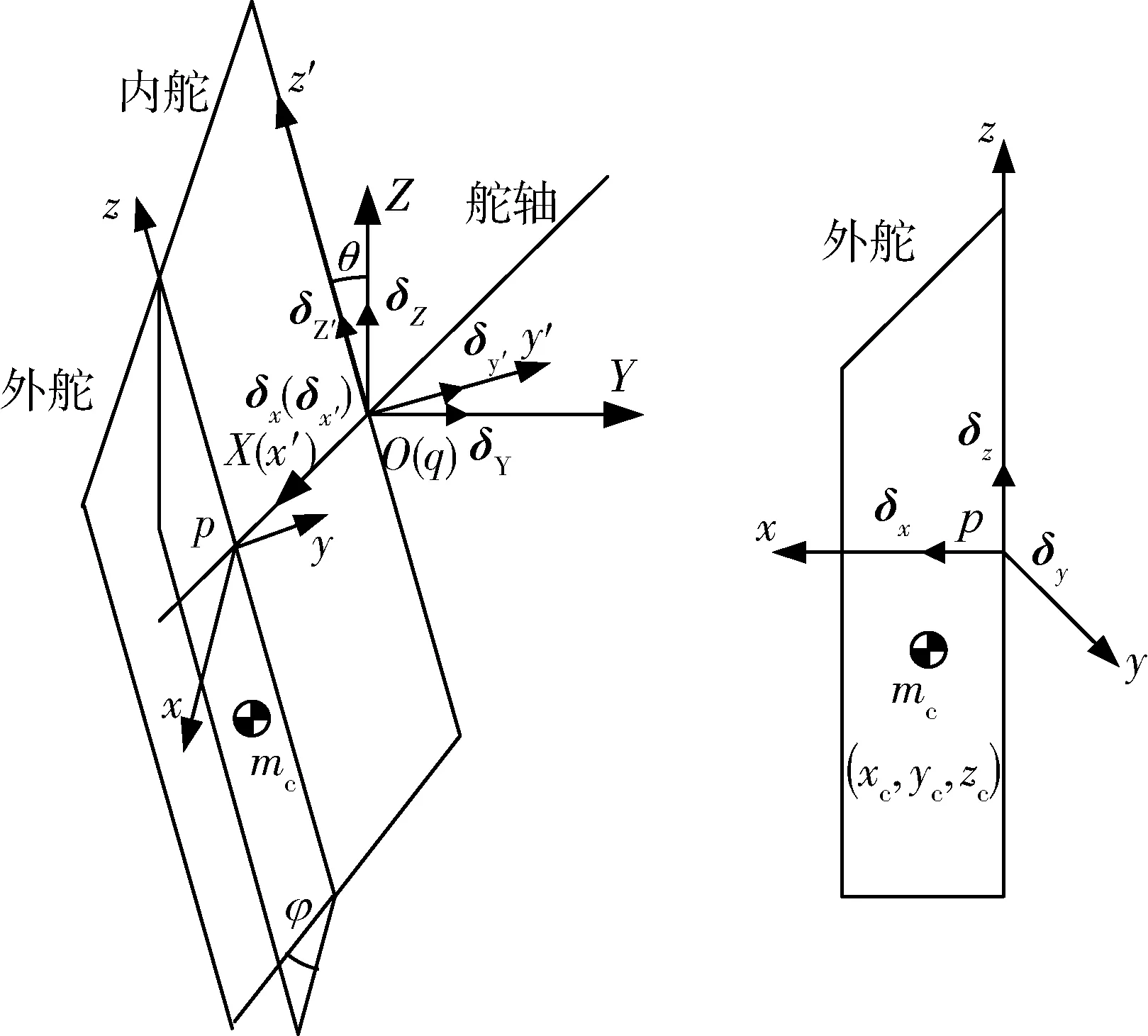
图2 折叠舵展开基本模型

矢量或张量在坐标系下的投影矩阵为沿该坐标系的各单位矢量或单位并矢量的对应分量组成的矩阵，本文中投影矩阵采用坐标原点加括号的上标来区分矢量或张量。设外舵以质心mc为原点的惯性张量为Jout_c，刚体平面上各点的法线必为该点的惯性主轴[16]，张量Jout_c平行于pxyz各坐标轴的投影矩阵为：

(1)

式中：A,B,C分别为外舵以质心为原点的惯性张量分别在x,y,z轴方向上的分量。

(2)

(3)

式中：Rop为旋转矩阵，

(4)

为了简化问题，折叠舵展开时内外舵间隙和变形忽略不计，展开到位后内外舵看做一个整体。以下分为展开阶段和冲击阶段对舵面展开进行分析。

1.2 展开段折叠舵动力学分析

展开阶段，外舵在燃气驱动下向外展开，内舵由于伺服系统在驱动力和燃气驱动耦合力作用下运动。忽略内外舵转轴与舵轴轴线的中心距，外舵的运动为绕动坐标系原点p的旋转运动，其动能Tout为：

(5)

式中ωout为外舵转动角速度矢量，其在惯性坐标系OXYZ下投影为：

(6)

类似地，对内舵动能Tin进行分析：

(7)

式中：ωin为内舵与舵轴的转动角速度矢量，Jin_q为内舵相对于原点q的惯性张量，计算公式为：

(8)

(9)

(10)

式中： (xcin,0,zcin) 为内舵质心在qx′y′z′坐标系下坐标，min为内舵质量，Ain,Bin,Cin分别为内舵相对于内舵质心的惯性张量分别在x′,y′,z′轴方向上的分量，ωin在惯性坐标系OXYZ下投影为：

(11)

若忽略重力势能的影响，列写拉格朗日函数：

L=Tout+Tin

(12)

基于拉格朗日定理，建立舵系统动力学方程为：

(13)

式中：

m12=m21=myczcsinφ-mxczccosφ

Q1=τ·i·η，τ为舵机电机转矩，i为电机到舵轴的减速比，η为传动效率。

Q2=Q(t)，Q(t)为舵面展开的驱动力矩。

由式(13)，m12包含xc和zc，外舵质心位置到舵轴延长线以与折叠舵轴线交点的距离决定了展开力矩对舵轴偏转扭矩的耦合程度。由于m12项和H1，H2项的存在。舵面展开动力学方程具有极强的时变性质和耦合性质。

舵面展开阶段，舵轴处的弯矩和扭矩是舵面展开时期的主要冲击部位。由动量矩定理，外舵的动量矩M是引起舵轴中心处产生的弯矩的唯一因素。列写OXYZ坐标系下动量矩方程：

(14)

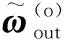
(15)

将动量矩投影于惯性坐标系OXYZ：

(16)

式中：Mx为冲击产生的舵轴转矩，由传动机构弹性变形以及电机伺服控制产生的力矩来吸收。My和Mz为施加于舵轴轴承上的弯矩分量，是冲击的薄弱位置，记其合力矩为：

(17)

1.3 冲击阶段折叠舵动力学分析

冲击阶段，外舵与内舵产生激烈碰撞，同时锁紧机构将内外舵锁定在展开状态，可视为内外舵产生了完全非弹性碰撞。此时由于舵面展开时燃气做功积累的能量在短时间内来不及释放，巨大冲量使舵轴，轴承甚至弹体产生弹性形变。通常情况下，舱体径向刚度要比切向刚度大，因此切向是主要冲击方向。冲击阶段在舵轴处引入了绕Z轴方向的旋转自由度，设外舵转轴与坐标原点O距离为d，如图3所示。

图3 展开到位冲击阶段折叠舵模型

碰撞前，外舵的旋转角速度投影于惯性坐标系OXYZ为：

(18)

(19)

由于碰撞时间极短，忽略碰撞短时间内的动量变化，列写OXYZ坐标系下动量守恒方程：

(20)

式中：Jall_o=Jout_o+Jin_o，为整个舵面相对于坐标原点O的惯性张量，其在惯性坐标系OXYZ下的投影为：

(21)

(22)

xcd=xc+d

(23)

内外舵展开到位后动坐标系pxyz平行于动坐标系qx′y′z′，因此有

(24)

(25)

式中：

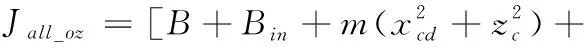
2 折叠舵展开安全优化控制

2.1 控制模型

建立舵面展开阶段的控制模型，由式(13)，可得系统逆动力学方程如下：

(26)

引入电机模型如下：

(27)

τ=KtI

(28)

式中：u为电机控制电压，L为电机绕组电感，R为电机绕组内阻，τ为电机扭矩，I为绕组电流，i为电机到舵轴的减速比，Ke为电机反电势系数，Kt为电机力矩常数。

定义系统状态变量为：

(29)

由式(26)～ (28)，可推导出系统状态方程：

(30)

式(30)的控制模型为仿射非线性系统，直接对其进行最优求解较为困难，通过数值计算不断逼近最优解是一条切实可行的途径。

2.2 启发式学习

根据式(30)的控制模型，以下基于启发式学习方法对控制输入制定学习策略。首先，基于控制周期将控制输入离散化，将控制时域划分为T,2T,3T，…，nT，对应控制输入：

u(kT)=uk,k=1,2,…,n

(31)

n为正整数，输入有界|uk|≤umax，控制点之间输入以样条曲线过渡。设计舵面展开评价函数为：

J=(k1tf)n1+(k2Mbmax)n2+(k3Tafter)n3

(32)

评价函数包括3部分：1)舵面展开到位时间tf，舵面能在指标要求的时间内展开是优化的前提； 2)舵面展开过程的最大弯矩Mbmax；3)舵面展开到位冲击后的内外舵共同运动的动能Tafter，以此表征冲击后舵面残余的能量。k1,k2和k3为线性权重参数，n1,n2和n3为指数权重参数。

基于式(32)的评价指标对式(30)的非线性系统进行终值时间不定的启发式学习优化设计。训练过程如图4，首先以随机初值输入给定u(kT)。依次对每个输入点进行上探索和下探索，探索步长Δu。对比上探索，下探索和原始状态的评价函数，如果评价函数优化则更新最优的输入序列u*。重复探索的过程，直至u*不变。接着缩小探索步长Δu，重复探索过程直到评价指标收敛速度足够小，即认为对最优解进行了足够精度的逼近。

图4 启发式学习流程图

3 仿真分析

依据实物测量值，将各参数以及燃气驱动力试验实测数据代入系统状态方程(30)，建立实物折叠舵控制迭代模型。令式(32)的评价函数各分量参数为：k1=100s-1，k2=0.01(N·m)-1，k3=0.002J-1，n1=n2=n3=1。根据图4的启发式学习流程对样本进行仿真迭代，直至参数稳定，获得逼近最优解迭代结果。

图5为经过训练前后的输入曲线对比，可见优化后的输入曲线为一条复杂曲线。图6为优化前后舵面展开角度曲线对比图，优化前后舵偏角变化不大，保证了舵面展开快速性指标。图9为弯矩曲线对比图，图中显示经过优化后最大弯矩从89.87N·m降到了75.75N·m，冲击后的动能从原来的397J降低至374J，冲击后残余动能为舱体冲击的主要原因，因此舵面展开对舱体的冲击减小了6%。

图5 启发式学习训练前后输入曲线

图6 舵面展开曲线训练前后对比图

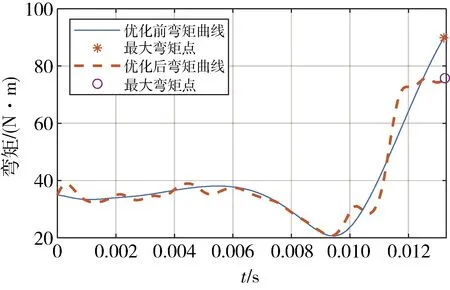
图7 展开阶段弯矩曲线训练前后对比

结合图5～7的分析， 0.008s前波动的输入量控制了外舵展开速度不受影响的同时，尽可能在展开过程中耗散掉积累的能量。而在0.012s后的输入反向，起到了抑制最后弯矩迅速增加的作用。

4 结论

针对折叠舵展开冲击大，过载高的情况，对展开过程中舵系统控制进行了优化，得出以下结论： 1)当外舵质心不在舵轴中心线上时，内外舵的展开具有强耦合的动力学特性；2)利用耦合特性，可以通过舵机伺服系统输入对展开时间、弯矩、冲击等因素进行优化控制； 3)利用启发式学习法，对舵面展开进行迭代仿真，可以使舵面展开安全性能得到优化，仿真结果表明，经过优化的输入可以使舵面在展开时间基本不变的条件下，舵轴的最大弯矩减小16%，碰撞后冲击载荷减小6%。