单晶锗纳米尺度分层多次切削的分子动力学模拟

杨晓京，余 证，刘 宁，赵 垒

(昆明理工大学机电工程学院，云南 昆明 650500)

1 前 言

单晶锗在半导体管、太阳能电池、红外光学仪器、微/纳电子系统等领域具有广泛的应用[1-3]。例如在微电子与光伏领域，锗的电化学性质稳定且与当前微电子仪器兼容性好[4]，与硅相比具有更高的电子和空穴迁移率，被视为传统半导体材料替代品[5]。另外，单晶锗对红外光具有较高的透过率，可被用来加工成复杂曲面的光学镜片[6]。然而，单晶锗是一种脆性材料，具有高硬度、高脆性、低断裂韧性等性质，难以通过传统的抛光、研磨等手段加工。单点金刚石切削(SPDT)是一种使单晶锗等脆性材料在纳米尺度下能够实现材料塑性去除的超精密加工方法，受到许多学者的关注[7-8]。但是，当采用SPDT方法在纳米尺度对单晶锗加工时，由于存在尺寸效应，无法利用现有的宏观切削理论对单晶锗材料的去除机理与表面成形/损伤行为做出解释，因此，有必要对单晶锗材料在纳米切削过程中的材料去除机制和表面损伤行为进行研究。

为了分析材料在切削过程中的去除机制和表面成形/损伤行为，近年来许多学者通过实验手段对硬脆材料纳米加工机理进行研究。比如，硅、4H-SiC这类脆性材料，一些学者开展SPDT，纳米压痕等实验，发现加工表面/亚表面存在非晶层和相变层。针对这一现象他们提出材料在高压作用下发生相变是材料塑性去除的主要原因[9-11]。此外，还利用纳米刻划实验分析了光学玻璃BK7[12]、微晶玻璃[13]等材料的去除机制和表面变形。然而，采用实验方法难以对纳米加工过程中材料去除机制和损伤机理进行分析，而分子动力学 (MD)仿真适合从原子尺度分析材料加工过程中的去除机制(即高压相变、晶体结构等)。例如，詹胜鹏等[14]运用MD模拟不同曲率半径的探针压入和刻划单晶铜工件，对材料的变形和磨损机理进行分析。Xiao等[15]利用MD分析6H-SiC在塑性域切削时的塑性变形机制。Wang等[16]使用MD方法对单晶硅进行纳米切削模拟，分析晶体各向异性对切削行为的影响。Zhu等[17]采用MD方法研究了Cu50Zr50非晶态合金在纳米切削过程中的去除和表面形成机制。

通过分析发现大多数MD模拟都是单次切削去除材料来分析材料去除特征。但是，从单次纳米切削模型获得理论不能够完全解释材料的切削机理、表面成形和损伤行为，因为在实际生产过程中，大多数加工过程都需要刀具多次切削去除材料形成新的表面。当第一次切削已经对加工表面造成损伤时，在随后切削中材料可能会发生不同的变形。目前一些学者对单晶铜，单晶硅等材料利用MD模拟SPDT重复切削，分析材料的变形行为，同时对已加工表面进行压痕模拟，分析加工表面的缺陷对材料力学行为的影响[18-19]。但是，上述研究侧重于分析加工表面硬度变化，没有对切削过程中晶体结构变化进行分析，其重复切削仿真模型与实际切削并不完全吻合。另外，目前对单晶锗纳米尺度分层多次切削过程中的表面/亚表面质量与去除机制的研究并不多见。因此，研究单晶锗纳米尺度分层多次切削过程中加工表面/亚表面损伤程度和相变，并且从晶体结构角度揭示材料去除机理是非常重要的。

本研究利用MD模拟金刚石刀具对单晶锗进行多次纳米切削，分析了晶体结构的演变和相变；同时比较了在相同的总切削深度下采用不同的两次预设切削深度加工单晶锗材料后表面/亚表面损伤程度和工件应力和温度的变化。通过对单晶锗多次切削过程中工件的晶体结构与原子配位数变化的研究，可以增加对实际加工时材料的去除与损伤机制的理解。

2 建模与模拟

2.1 MD仿真模型与势函数

图1为三维单晶锗纳米尺度多次切削仿真模型，三维模型由单晶锗工件和两个几何参数相同的金刚石刀具组成。单晶锗工件的大小为40 a×25 a×20 a(a为锗的晶格常数，a=0.567 nm)，工件的三维方向为X-[001]，Y-[100]，Z-[010]。单晶锗工件被分成三个部分：边界层原子、恒温层原子、牛顿层原子[20]。为了阻止工件在切削时移动和保持晶体结构对称，将左边与底部的两层边界层原子固定。与边界层原子相邻是恒温层原子，左边与底部的两层恒温层原子主要是保持温度恒定，以模拟环境温度对工件热耗散。牛顿层原子遵循牛顿运动定律。在切削过程中为了有效地模拟多次切削过程，将金刚石刀具设置成一样的几何参数。刀具的前角为10°，后角为15°，刀尖圆弧半径为2 nm，刀具宽度为4 nm。由于金刚石硬度远大于单晶锗，所以在切削过程中金刚石刀具被设置为刚体[21]。

图1 单晶锗纳米尺度多次切削分子动力学模型Fig.1 Molecular dynamic model for multi-cutting of single crystal germanium in nanoscale

选择合适的势函数，对MD仿真结果的准确性和可靠性至关重要。Tersoff势函数对共价键原子相互作用的描述具有很高的精确性，在描述Si-Si, C-C, Si-C原子之间相互作用时取得很好的效果。基于之前的研究选用Tersoff势函数作为Ge-Ge原子之间相互作用的描述[21-24]。使用Morse势函数描述Ge-C原子的相互作用，Morse势函数的参数为[25]：结合能D=0.125778 eV，弹性模量α=2.58219 Å-1，平衡距离γ0=2.2324 Å。由于金刚石刀具被视为刚体，所以C-C原子不需要指定相互作用势函数。为了降低模型的尺寸效应，满足目前的计算能力，在Z方向使用周期性边界条件。工件的Z-X表面是加工表面，所以采用自由边界条件。

2.2 仿真模型初始化与切削参数设置

切削仿真的加工参数如表1所示，为节约计算时间，仿真设定的切削速度远大于实际加工速度，但是相关学者指出在纳米切削过程中切削速度对切削过程的影响不大，且目前依然有许多学者采用大的切削速度[16,26]。在切削之前，使用共轭梯度法对模拟体系进行能量最小化，原子的初始速度服从麦克斯韦-玻尔兹曼分布，采用Nose-Hoover控温方法(NVT)将体系温度控制在298 K，弛豫时间为15 ps。在切削过程中，只对恒温层进行控温，模拟环境对切削热能的耗散作用。

表1 MD仿真模型的加工参数Table 1 Processing parameters of the MD simulation model

为了模拟多次切削过程，研究切削过程中加工表层/亚表层质量和去除机制。设定总的切削深度为4 nm，刀具第一次切削深度分别为1、2、3和4 nm；基于总的切削深度与前一次切削深度，第二次切削深度分别为3、2、1和0 nm。多次切削过程中刀具运动轨迹如图2(a)所示，在弛豫结束之后，首先，Tool1在预设切削深度下，沿着X轴的负方向从工件最右端移动至距离右端16 nm处；其次，Tool1退到工件上方，避免在下次切削时对工件产生相互作用；最后，Tool2在预设切削深度下沿着同样的路径移动至距离工件最右端9.5 nm处。图2(b)为切削仿真过程中的时间步长。模拟结束后，使用OVITO软件对模拟结果进行可视化，分析晶体结构的变化。

图2 多次切削过程中刀具运动轨迹示意图(a)和时间步长(b)Fig.2 Schematic diagram of tool movement trajectory (a), and timestep (b) during multi-cutting processes

3 结果与讨论

3.1 单晶锗材料的晶体结构与去除机制分析

图3为不同预设切削深度下切屑与工件晶体结构图(在x-y平面截取与刀具宽度相同的工件作为晶体结构图)。从图中看到，灰白色原子主要分布在工件的已加工表面/亚表面和切屑当中，表明单晶锗原子结构已经由金刚石结构向无定形结构转变，这在脆性材料单晶硅切削过程中也同样出现[18]。绿色原子区域是工件表面，由于表面原子缺少近邻原子，所以提取时被视为有缺陷的金刚石结构。蓝色原子区域是无缺陷的金刚石结构，表示晶体没有发生结构变化。从图3(a)～(d)看出，随着切削深度的增加，工件表面上的切屑体积越来越大，亚表面无定形结构原子厚度增加，说明切削深度直接影响材料的去除量与亚表面损伤深度。切屑的产生是由于在高温和剪应力作用下Ge-Ge键键长和键角增大并且剧烈波动使得Ge-Ge键键能减弱[27]，当刀具推挤产生的能量超过Ge-Ge键键能时原子键发生断裂，而带有锗悬键的锗原子具有很高的能量和活性，会重新和其它原子形成稳定的共价键，因此当原子键发生断裂后部分原子在推挤作用下发生塑性流动形成切屑。并且受刀具挤压作用切削区域内的原子晶格发生了剪切和挤压变形使原子结构从金刚石结构转变成无定形结构。Wang等[16]提出当脆性材料在高压作用下被去除时切屑为无定形结构，发生塑性去除；当高压相变不易发生时，刀具的推挤使得材料解理面的剪切应力超过材料屈服极限时，材料发生解理，切屑出现微晶结构，发生脆性去除。而图3中切屑和已加工表面是无定形结构，所以切屑是被塑性去除。另外，从图可见，受到刀具挤压后亚表面金刚石结构表面呈锯齿形，并且随着深度的增加更加明显。这是由于切削深度增加垂直载荷加大，使得刀具后刀面挤压作用更突出。图3(b)、(c)、(d)和(g)标记为Ⅰ～Ⅳ处，出现了六方金刚石结构原子，六方金刚石结构原子主要位于已加工亚表面的无定形结构原子与金刚石结构原子交界处。这是由于刀具切削后，加工表面温度和应力降低，无定形结构转变为六方金刚石结构，类似于退火过程[28]，而当压力与温度进一步释放后，切屑区Ⅵ处甚至出现了金刚石结构原子。

图3(a)～(d)是第一次切削后晶体结构图，(e)～(h)是第二次切削后晶体结构图。图3(e)、(f)、(g)与(d)比较发现，当总的切削深度相同时采用多次切削方式加工的工件亚表面损伤层深度比单次切削小，且加工表面更加平滑。同时比较(e)、(f)、(g)图之间发现，(g)图的亚表面损伤层深度最小。说明当总的切削深度一定时，采用第一次切削深度比第二次切削深度大的切削模式能获得更好的加工表面。对图3(e)～(h)中第一次切削留下的切屑分析发现，没有受到刀具推挤后，切屑体积明显增大。同时，切削区无定形层厚度d3、d4大于d1、d2。说明切削完之后，无定形层原子由于压力和温度释放发生弹性回复，造成无定形层厚度增加。

图3 不同预设切削深度下切屑与工件晶体结构图 (a)～(d)第一次切削时的加工深度分别为1 nm、2 nm、3 nm和4 nm；(e)～(h)第二次切削时的加工深度分别为3 nm、2 nm、1 nm和0 nmFig.3 Crystal structures of chips and workpieces at different preset cutting depths (a)-(d) the processing depths of the first cutting are 1 nm, 2 nm, 3 nm and 4 nm, respectively; (e)-(h) the processing depths of the second cutting are 3 nm, 2 nm, 1 nm and 0 nm, respectively

图4为多次切削过程中亚表面损伤深度与实际加工深度。从图4(a)可见，随着切削深度增加，亚表面损伤深度增加，但切削深度超过3 nm后损伤层深度增幅降低。第二次切削时，亚表面损伤深度随预设切削深度的降低而降低，而第二次切削深度为0 nm时，损伤层深度上升是因为Tool2没有切削工件而是挤压加工表面，导致亚表面损伤层深度增加。表明亚表面损伤深度不受第一次加工深度影响，仅与最终加工深度相关。对图4(b)第二次切削后的实际加工深度曲线分析，可以得出当第一次切削深度比第二次切削深度大时材料去除量最好。总切削深度相同的条件下，多次切削的实际加工深度要大于单次次切削，这是由于第一次加工之后工件表层覆盖的无定形层原子的硬度与密度小于金刚石结构原子，更容易被去除[20]。

图4 多次切削过程中的深度变化曲线 (a) 亚表面损伤深度； (b) 实际加工深度Fig.4 Depth curves during multi-cutting process (a) subsurface damage depth; (b) actual processing depth

3.2 纳米尺度多次切削过程晶体相变分析

为了分析多次切削过程中单晶锗的相变，计算了工件原子的配位数。图5是不同预设切削深度下原子配位数分布图(在x-y平面截取与刀具宽度相同的工件作为相变原子分布图)，图中颜色依据原子配位数的大小标记，配位数为4的原子(金刚石结构)被删除。淡蓝色的原子是配位数为2的表层原子。从图中看到配位数大于4的原子主要分布在切屑和已加工表面/亚表面中，这是由于工件原子受到刀具挤压和剪切使得晶格结构发生变形，造成了原子配位数增加从而发生相变。而由图7分析发现多次切削过程中的原子相变与一些学者依据纳米压痕仿真提出的当静水压力超过某一阈值后，单晶锗原子从金刚石结构(Ge-Ⅰ)转变为β-tin结构(Ge-Ⅱ)的相变理论一致，并且指出β-tin结构原子的配位数是6，配位数为5的原子表示一种将会转变为β-tin结构的中间结构，配位数为7的原子表示一种类似于液态的非晶结构[25,29]。图5(a)～(d)是第一次切削后原子配位数分布图。从图可见，相变原子体积和数量受切削深度的影响，切削深度越大亚表面相变层厚度也越大。造成这种情况的直接因素是由于切削深度变大使得刀具对工件的垂直作用力增加导致更多的Ge-Ⅰ 结构原子发生相变。从图中还可以看到，刀刃口与工件接触区和前刀面与切屑接触区有大量配位数为7的原子，这是因为刀具在运动过程中，前刀面和刀刃口对工件挤压使得接触区应力和温度增大，造成了原子发生非晶相变，从而导致材料以塑性方式去除。图5(e)～(h)是第二次切削后原子配位数分布图，从图中看到第一次切削后的切屑区与切削区配位数为6、7的原子数量明显减小。这是由于切削之后，经过一段时间非晶结构原子与β-tin结构原子会重新转变为Ge-Ⅰ结构，这一现象和其他学者分析结果一样[30]。另外，对比图5(e)～(h)中亚表面相变层厚度发现，图5(g)的相变层厚度最薄，说明采用预设切削深度为3/4 nm的加工方式切削的工件质量最好，这与第3.1节分析得出的结论相一致。同时，对比(b)图和(f)图亚表面相变层厚度发现，当两次切削深度相同时，第二次切削后的亚表面损伤层厚度小于第一次切削后的损伤层厚度，表明多次切削能提高加工表面质量。

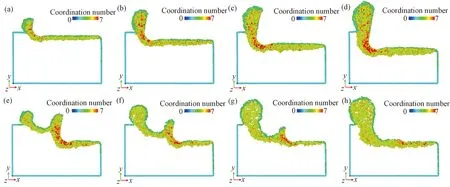
图5 不同预设切削深度下原子配位数分布图 (a)～(d)第一次切削时的加工深度分别为1 nm、2 nm、3 nm和4 nm；(e)～(h)第二次切削时的加工深度分别为3 nm、2 nm、1 nm和0 nm(配位数为4的原子被删除)Fig.5 Distribution of atomic coordination number at different preset cutting depths (a)-(d) the processing depths of the first cutting are 1 nm, 2 nm, 3 nm and 4 nm, respectively; (e)-(h) the processing depths of the second cutting are 3 nm, 2 nm, 1 nm and 0 nm, respectively (The atom with coordination number 4 is deleted)

为了更清晰地了解在多次切削过程中相变原子数量的变化，将四种不同预设切削深度切削后的工件相变原子数进行统计，如图6所示。从图中看到配位数为5的原子数量明显多于配位数为6、7的原子，配位数为7的原子最少，这是由于在切削过程中大量Ge-Ⅰ结构原子转变为中间结构，当切削区应力超过一定值时，一部分转变成β-tin结构，另一部分在更大的应力和高温下转变为非晶结构。第一次切削过程中，配位数为5、6和7的相变原子数量明显增加，尤其是配位数为5的原子，由此确定相变原子增加量与切削深度密切相关，这与前面的结论相一致。刀具未切削时，相变原子数量明显下降，说明应力和温度释放导致相变原子重新转变成金刚石结构或其它晶体结构，如六方金刚石结构。对图中第二次切削过程中的相变原子数量分析发现，(a)、(b)图中相变原子继续增加，而(c)、(d)图中相变原子基本不变或下降。

图6 多次切削过程中原子的配位数变化曲线 (a) 1/3 nm; (b) 2/2 nm; (c) 3/1 nm; (d) 4/0 nmFig.6 Coordination curves of atoms during multi-cutting processes (a)1/3 nm; (b) 2/2 nm; (c) 3/1 nm; (d)4/0 nm

径向分布函数(RDF)是一种能够描述晶体结构变形的分析方法，利用RDF可以分析单晶锗工件结构和原子键长的变化。切屑和切削前工件的RDF，如图7(a)所示。从图中看到加工前工件的RDF曲线表现出短程和长程都有序，最近邻原子间距为2.4 Å，而切屑原子的RDF曲线表现出短程有序而长程无序,这与LAI等[31]计算的非晶锗原子的RDF曲线类似，这说明切屑原子为非晶结构。图7(b)为四种不同切削情况下加工之后的单晶锗工件径向分布函数。从图中看到当预设切削深度为1/3 nm、2/2 nm、3/1 nm的峰值位置为2.45 Å，4/0 nm的峰值位置为2.5 Å，而β-tin结构原子的键长为2.53 Å[31]，说明工件的亚表面原子结构从Ge-I结构转变为β-tin结构，从而使得加工后的单晶锗工件RDF峰值位置右移，证实了前文的分析是合理的。同时，从图中看到原子间距为2.45 Å处的峰值降低，这是由于切削量增加，导致更多原子发生相变造成的。

图7 径向分布函数曲线 (a) 加工前工件原子和切屑原子; (b) 加工后工件原子Fig.7 Radial distribution function curves (a) workpiece atoms before processing and chip atoms; (b) workpiece atoms after processing

3.3 应力和温度分析

分析多次切削过程中单晶锗工件的应力和温度，对了解单晶锗结构演变和表面/亚表面损伤程度具有重要意义。使用式(1)计算不同切削模式下单晶锗工件的温度[32]：

(1)

式中：N是原子数，kB是玻尔兹曼常数(1.3806503×10-23J/K),vi是i原子的速度，T代表原子的温度,Ek是系统的动能，mi是原子的质量。

同时，使用式(2)计算静水应力：

(2)

式中：σHyd是静水应力，σxx是切向应力,σyy是法向应力，σzz是侧向应力。

工件的平均应力和温度曲线，如图8所示。从图可见，第一次切削过程中的应力和温度受初始预设切削深度影响，特别是温度和切向应力随初始预设切削深度呈直线增加。第二次切削过程中应力和温度的变化趋势与第一次切削相反，但其变化趋势也受到切削深度的影响。多次切削过程中第一次切削的温度比第二次切削变化剧烈，这是因为第一次切削金刚石结构的表面时释放的能量比第二次在非晶结构表面切削时多，此外经过初次切削之后，加工表面软化使得第二次切削力变小，所以第二次切削中温度没有剧烈变化。与此同时，切向应力和静水应力受切削深度影响明显，对比图5中配位数为7的原子数量发现，其数量变化与切向应力和静水应力的变化趋势一致，说明切向应力和静水应力是影响工件原子发生相变的主要原因。当初次切削深度接近或超过总切削量的一半时，前后两次切削过程中工件的平均切向应力和静水应力相同，此时工件内部应力均衡有利于形成较好的加工表面。而图8(c)中第一次切削后法向应力的变化没有第二次切削的剧烈，但其值超过第二次切削时的应力，这是因为第一次切削时加工表面的弹性回复大，且第一次切削的实际加工率小于第二次切削，所以垂直切削力大，但其变化相对平缓，从而导致工件法向应力大但变化较小。对比图4(a)中加工完成后的工件亚表面损伤层深度可以看出，其变化规律与法向应力一致，说明法向应力是影响亚表面损伤厚度的主要原因。另外，在预设切削深度为0 nm的第二次切削中，法向应力值上升是因为刀具再次挤压产生的应力和初次切削产生的应力积累导致其上升的。

图8 工件的平均应力和温度曲线 (a) 温度; (b) σxx; (c) σyy; (d) σHydFig.8 Average stress and temperature curves of the workpiece (a) temperature; (b) σxx; (c) σyy; (d) σHyd

4 结 论

本研究通过MD模拟金刚石刀具对单晶锗工件进行纳米尺度分层多次切削，分析了多次切削过程中单晶锗结构演变、表面/亚表面损伤程度和相变以及工件应力和温度的变化。得出如下结论：

1. 切削过程中，在刀具的推挤作用下切削区原子发生高压相变，原子结构从金刚石结构(Ge-Ⅰ结构)转变为无定形结构(β-tin结构或非晶体结构)，从而使得材料发生塑性变形并且切屑以塑性方式去除。切削结束后由于压力和温度的释放，无定形层原子发生弹性回复，使得损伤层厚度增加，少量无定形结构原子重新转变为Ge-Ⅰ结构或六方金刚石结构。通过径向分布函数分析发现，加工表面/亚表面和切屑的无定形结构原子，主要是β-tin结构和非晶体结构。

2. 预设切削深度增加材料的去除量和亚表层损伤深度增加。亚表面损伤深度不受前一次切削深度影响，仅与最终预设切削深度相关。当两次预设切削深度接近或初次切削深度大于再次切削深度时，材料去除量最好。并且在同样的切削条件下，多次切削比单次切削更有利于降低亚表面损伤深度和提升加工效率。

3. 工件内部的平均温度和应力随预设切削深度的增加而上升。工件原子相变与切向应力σxx和静水应力σHyd相关，亚表面损伤厚度与法向应力σyy相关。当两次预设切削深度接近或相等时，前后两次切削过程中的平均切向应力σxx和静水应力σHyd相同，此时工件内部应力均衡，有利于形成较好的加工表面。