基于位置差的特征序列挖掘快速算法*

潘向荣，王 婷

(1.中国西南电子技术研究所，成都 610036；2.电子科技大学 通信抗干扰技术国家级重点实验室，成都 611730)

0 引 言

公开通信协议的数据帧结构是确定并易知的，但在某些特殊场景尤其是军事应用环境中，为提高数据传输的安全性，通信方通常不会采用公开的通信协议，而是采用专用的通信协议进行数据传输，这些专用通信协议通常是不公开的。因此，在电子对抗中，数据帧格式对非合作接收方而言是未知的，从侦查截获的通信比特流中识别出帧结构进而识别通信协议，将协议帧头与数据载荷区分开来，从而进一步对截获的数据载荷进行破译等分析，对分析网络拓扑结构、识别信息流目标以及网络抗干扰通信具有重要意义。

目前，国内外对数据链路层未知协议的识别领域的研究进展较为缓慢[1-10]。“未知协议”是指具有一定固定帧头格式的未公开协议。比特流未知协议识别的一般思路是：基于统计理论挖掘出比特流的特征序列等协议特征，根据一般通信协议的基本特征来进一步确定比特流的帧头位置，进而分析出比特流的帧格式。对于未知的通信协议，分析者并没有可以参考的特征序列，必须通过枚举和统计方法来筛选、比对等步骤挖掘出特征序列。从比特流中如何快速、准确的分析出特征序列是识别未知通信协议的关键。

一般说来，未知通信协议识别包括数据预处理、频繁序列提取(统计与筛选)、特征序列挖掘和特征序列关联分析4个主要步骤。

数据预处理是指将获取的数据转换为01比特流，频繁序列提取是指对模式序列进行准确计数，并通过预设阈值，根据一定的筛选规则筛选出频繁序列，然后通过拼接等手段获得较长的频繁序列，从而得到候选特征序列集合。最后，应用关联规则挖掘技术对候选特征序列进行关联规则挖掘，由此确定未知通信协议的特征序列和可能的协议帧结构。

文献[2]采用AC(Aho-Corasick)统计算法完成频繁序列的提取(包括统计与筛选)。该算法基于二叉树来实现对模式序列出现位置的存储。在对模式序列进行统计计数时需要遍历整棵二叉树节点，其遍历代价很大。本文在分析出AC快速统计算法[2]的这一缺陷后，改进了模式序列的统计方式，采用数组代替二叉树存储比特流中模式序列的位置信息，并构造了使得数组下标值与二叉树节点值保持一致的关系式，有效降低了对模式序列进行计数及筛选的时间复杂度。进一步，本文将存储各频繁序列位置信息的数组依次连接成一个长数组，并按频繁序列出现位置的先后顺序重新排列该数组元素，进而改进了基于位置差的特征序列挖掘算法。与原算法相比，改进算法大幅度减少了算法迭代次数，将频繁序列拼接时间减少了至少一个数量级，快速挖掘出了比特流中的特征序列。

1 相关概念

设有长度为n的随机比特流序列S，对于S中的任意一个模式序列P，不妨给出如下定义：

定义1 假定P中包括m个比特，则称P的长度为m。

定义2 假定P为长度m的模式序列，Q为长度q的模式序列，q≤m，且P的1～q位均与Q的对应位置比特相同，则称Q是P的子序列，P是Q的父序列。

定义3 假定S中共有r个长为m的模式序列，其中模式序列P出现了k次，则P的支持度supp(P)为k/r。

定义4 假定supp(P)不小于用户规定的最小支持度，那么P为频繁序列；反之，为非频繁序列。

2 基于位置差的特征序列挖掘快速算法

2.1 AC快速统计算法的改进

AC算法是于1975年由贝尔实验室的Aho和Corasick两位研究人员提出的一种多模式匹配算法，该算法是模式匹配领域的经典算法之一。金陵等人[2]提出的AC快速统计算法是基于AC算法的一种改进，该算法将二叉树存储结构改为使用数组结构进行比特流中模式序列的存储，可以实现对比特流中出现的所有模式序列统计完全。

显然，比特流序列的元素取值为0或1。因此，长为m的模式序列P有且仅有两个长为m+1的父序列。穷举长度取值为[1，m]的所有模式序列可构成一棵完全二叉树。图1表示由长度区间为[1，4]b的所有模式序列构成的二叉树。

图1 长为1～4 b的模式序列所构成的完全二叉树

AC快速统计算法基于二叉树来实现对模式序列出现位置的存储。在对模式序列进行计数时需要遍历整棵二叉树节点，其遍历代价很大。

经过对二叉树存储结构和相关存储结构特点的深入分析，采用数组代替二叉树存储比特流中模式序列的位置信息，并构造了使得数组下标值与二叉树节点值相等的关系式，基于此给出了一种复杂度更低的模式序列统计算法。该算法的创新之处在于，通过对所截获的比特流的存储结构的修改，使得在对模式序列的计数过程中极大降低了对模式序列的扫描次数，进而极大减少了统计过程中所需的计算时间和存储空间。

本文对文献[2]中的AC快速统计算法进行了改进，通过分析各模式序列与数组下标之间的逻辑关系，构造了使得存储模式序列对应的数组下标值与二叉树节点值相等的表达式，具体为

Index= dec(x)+2Length(x)-1

(1)

式中：x表示模式序列，dec(x)表示x对应的十进制数，Length(x)表示x的长度，Index表示x在存储其位置信息的数组中的下标值。

根据式(1)，所有的模式序列均与存储其位置的数组的下标值对应。将图1中的二叉树采用式(1)列出模式序列与存储其位置的数组的下标号之间的对应关系,如表1所示。

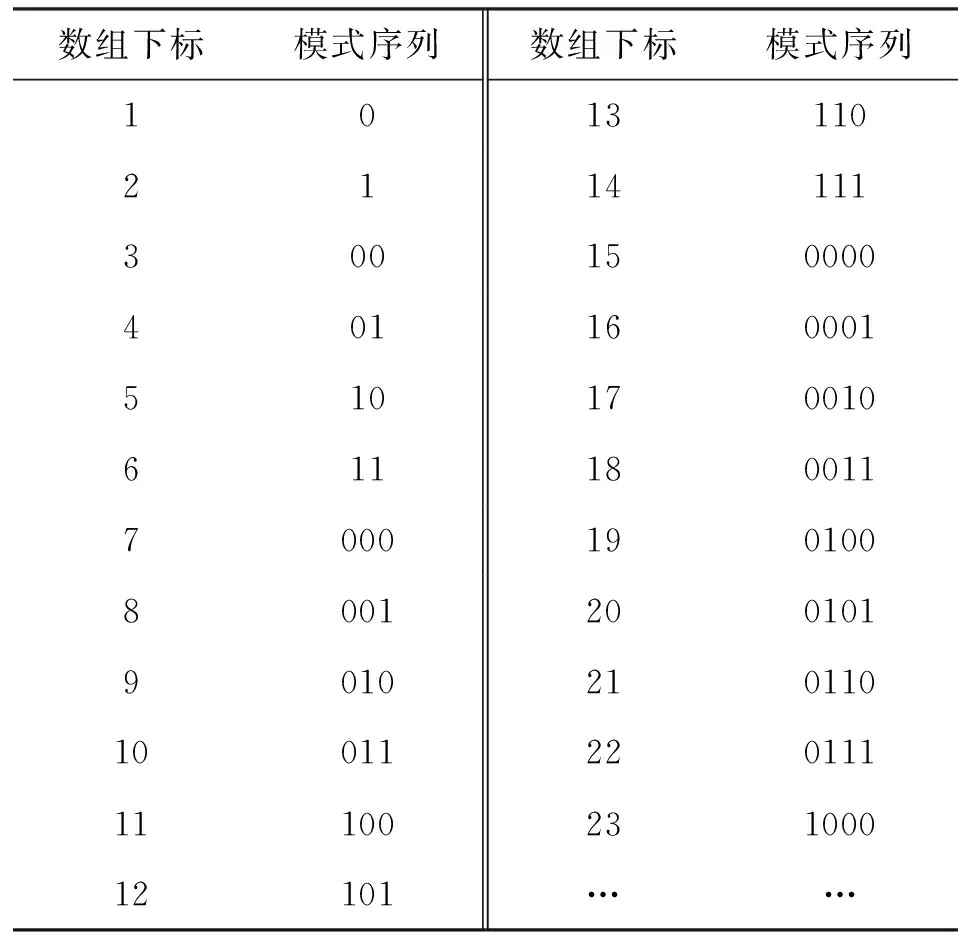
表1 模式序列与数组下标的映射关系

将表1和图1进行比较，不难发现如下事实：比特流中各模式序列在数组中的下标值与这些模式序列在二叉树中的节点值完全对应。这一事实可以更为直观地比较模式序列在二叉树结构和数组结构下的存储特征。

2.2 基于阈值的频繁序列筛选

在无任何先验信息情况下，假设对长度为m的模式序列进行计数，不失一般性，假定0和1等概率出现在每一个比特位置上，那么，长为m的模式序列的种数为2m。不妨假定待识别的比特流S的随机性良好，那么每种长为m的模式序列的出现概率均为1/2m。根据支持度的定义，则长度为m的模式序列的平均支持度等于1/2m。不难得知，长为n的比特流S中存在(n-m+1)个长度为m的模式序列。因此，长为m的模式序列出现的平均次数为(n-m+1)/2m。

通常，筛选阈值Th被设置为

(2)

式中：参数α的作用为调节阈值大小，n表示序列S的长度，m表示模式序列的长度。

在所有的模式序列的计数和阈值设置完成以后，根据对比模式序列的计数值与筛选阈值的大小以及筛选规则，可将所有的模式序列划分为频繁序列和非频繁序列，所有被列为频繁序列的模式序列构成频繁序列集合。

2.3 基于位置差的长序列拼接改进算法

一般来讲，子序列的出现次数均大于其父序列的出现次数。因此，子序列被筛选为频繁序列的机会大于其父序列。换句话说，频繁序列集合中更多的是长度较短的模式序列。但在实际协议中，也会存在长度较大的特征序列。序列拼接是获得较长模式序列的一种主要方法之一，即将满足一定要求的较短的频繁序列通过拼接的方式获得较长的模式序列。

文献[2]介绍了一种基于位置差的长序列拼接方案，但该方案在对短序列进行拼接的过程中需要大量的重复迭代操作。经分析，该序列拼接算法存在如下三个不足：第一，复杂度高；第二，存在特征序列挖掘误差；第三，序列重叠度高。本文从这些分析结果出发，对基于位置差的长序列拼接算法进行了改进。改进算法充分利用了各频繁序列在比特流中出现位置的先后顺序这一信息，在对频繁序列集合进行存储表示时，改进算法按照各频繁序列的出现位置来进行存储。这一改进大幅简化了拼接过程中的迭代次数。

在文献[2]中，将同种频繁序列出现的多个位置信息存储在同一个数组中，如表2所示。

表2 频繁序列与其出现位置对应表

在表2中，xi(i=1,2,…,N)表示第i种频繁序列，而pi,j表示第i种频繁序列的第j个出现位置。这种频繁序列与表示其出现次数位置的数组之间的对应关系，不能准确刻画出这两个频繁序列间的出现位置的先后顺序。例如，无法直接判断出模式序列p1,1和p2,1的大小关系，只能分别将这两个模式序列的数值取出并进行比较才能做出判定。这直接导致了该拼接算法的复杂度较高。

基于对AC快速统计算法的不足的分析，本文提出了改进算法。改进算法在基于表2所示的存储方式上，将各模式序列对应的所有数组依次首尾连接成一个数组P，如表3所示。显然，此时频繁序列出现位置的总数，即为频繁序列集合的元素个数。

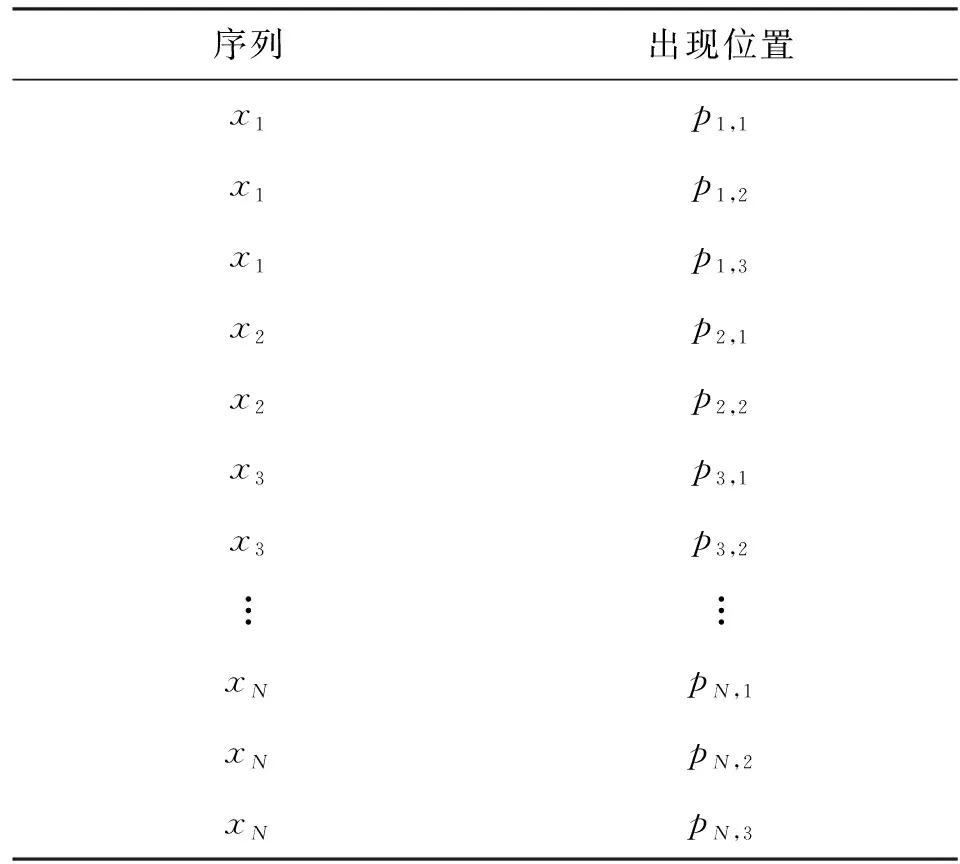
表3 频繁序列与其出现位置一一对应表

进一步，将数组P中的元素按照相应频繁序列出现位置的先后顺序从左到右进行排序，然后，进行基于位置差的长序列拼接，其拼接算法流程如图2所示。

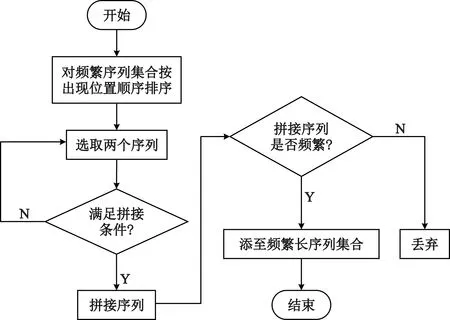
图2 基于位置差的长序列拼接算法流程

将满足如下拼接条件的两条频繁序列xi和xj进行拼接，然后对拼接后的长序列进行筛选，判断其是否为频繁序列。拼接条件仍然为[2]

pos(xj)- pos(xi)=Length(xi) 。

(3)

式中：pos(xi)和pos(xj)分别表示序列xi和xj在输入比特流中的出现位置。这里需要指出的是，因为改进算法的拼接条件与原算法一致，因此，拼接而成的长序列的输出结果与原算法也完全相同。

基于位置差的长序列拼接改进算法的伪代码如下：

1 初始化XS=∅,P=∅;

2 fori=1 to length(Xs) do

6 end for

7 end for

8 对P进行由小到大的排序，并对X进行对应的元素交换；

9 初始化i←1,j←i+1,Xtemp=∅;

10 while true do

11 ifP[j]-P[i]=length(X[i])then

12xnew←splice(X[i],X[j]);

13 ifxnex∉Xtempthen

14Xtemp←Xtemp∪xnew,pos(xnew)←pos(xnew)∪i;

15 else

16 pos(xnew)←pos(xnew)∪i;

17 end if

18i←i+1,j←j+1;

19 else ifP[j]-P[i]>length(X[i])then

20i←i+1;

21 else

22j←j+1

23 end if

24 if j=length(X)+1 then

25 ifXtemp=∅ then

26 break;

27 else

28 筛选Xtemp中满足阈值的频繁序列，并将筛选出的序列集合展开为Xsel以及其出现位置集合Psel;

29 ifXsel=∅ then

30 break;

31 end if

32 对Psel进行排序，Xsel也对应进行排序；

33 初始化k←1,l←1;

34 while true do

35 ifP[k]=Psel[l] then

36X[k]←Xsel[l],k←k+1,l←l+1;

37 else

38k←k+1;

39 end if

40 ifl=length(Psel)+1 then

3 算法分析及算法有效性验证

与原算法[2]相比，本文提出的改进算法采用一个数组来存储所有频繁序列的位置信息，且数组元素依照对应频繁序列出现位置的先后顺序从左到右依次排列，该存储方式极大减少了算法的迭代次数。在原算法[2]中，需要扫描所有可能的位置差来判断拼接条件(式(3))是否满足，极大增加了算法中的迭代操作，导致原算法的复杂度较高。改进算法在拼接过程中只需要遍历频繁序列集合一次，极大减少了迭代地进行拼接条件的判断操作，使得改进算法的复杂性大大低于原算法。

为验证算法的有效性，我们采用Visual C++开发平台编写程序实现算法，使用Wireshark抓包软件截取数据包完成了算法性能有效性测试实验。测试环境为Windows 7操作系统，Intel®CoreTMi5 7400处理器，CPU主频3 GHz。

测试实验方案的步骤如下：

Step1 使用Wireshark抓包软件截取ARP包(200帧以上)进行测试，以包含100帧ARP协议帧的比特流作为实验数据。

Step2 设置5组筛选阈值，分别为0.5、1.0、1.5、2.0和2.5。

Step3 对Step 1得到的实验数据分别采用原算法[2]和本文的改进算法完成对实验数据的比特流分析。

Step4 对比两种算法下的时间复杂度。

表4给出了在不同阈值下上述两种长序列拼接算法的仿真运行时间。

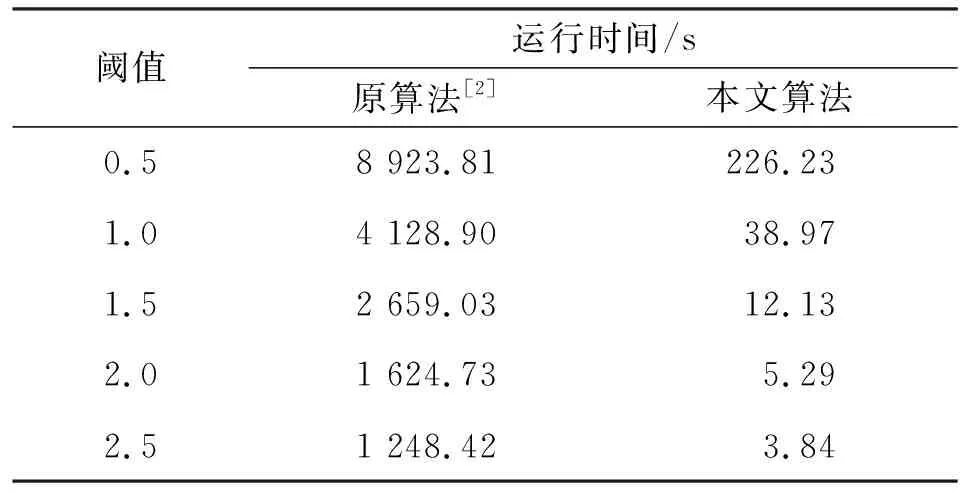
表4 不同阈值系数下两种序列拼接算法的运行时间

从表4中的仿真数据可以得到以下结论:第一，随着筛选阈值从0.5到2.5以0.5为步长逐渐增大，两种拼接算法的计算时间均逐渐减少；第二，改进算法的时间复杂度远低于原算法，表明对频繁序列出现位置进行排序后再进行拼接的方案极大降低了拼接算法的时间复杂度，验证了改进算法的有效性。图3形象地展示了两种算法的时间性能对比。

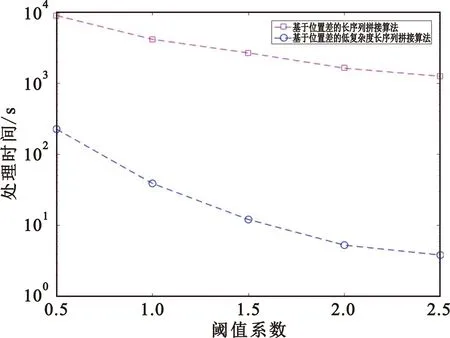
图3 两种序列拼接算法的时间复杂度比较

4 结 论

链路层中基于比特流的帧结构分析是进一步获取情报信息的关键环节。金陵等人[2]提出的基于位置差的长序列拼接算法是面向比特流未知协议识别的主要算法。本文在深入研究该算法基础上，提出了基于位置差的特征序列挖掘改进算法。改进算法采用数组来替代原算法中的二叉树来存储频繁序列的出现位置信息，且数组元素依照对应频繁序列出现位置的先后顺序从左到右依次排列，这种存储方式极大减少了算法的迭代次数。最后，使用Wireshark截取ARP包完成了算法的有效性测试。仿真结果表明，与原算法相比，本文的改进算法大幅度减少了算法迭代次数，将频繁序列拼接时间减少了至少一个数量级，快速挖掘出了比特流中的特征序列，为进一步挖掘比特流的帧内结构奠定了基础。