全空域球面相控阵测控系统角跟踪方法概论*

杜 丹，王文政，扈景召

(中国西南电子技术研究所，成都 610036)

0 引 言

随着我国航天技术和“北斗”导航系统的快速发展，在轨的侦察卫星、海洋监视卫星、通信卫星、导航卫星以及其他低轨飞行器的数量在未来十年内将快速增长。为了在同一时刻完成多个飞行器的管理，测控系统必须具备多目标运行管理、多目标同时跟踪测量的能力[1-2]。

数字多波束球面相控阵测控系统是一种新的测控通信架构[1-2]。由于采用对多个动态目标的数字波束实时指向，需要知道动态目标的实时位置信息，解决数字多波束相控阵系统对动态目标的实时信号接收问题，即需要得到对动态目标的无偏来波估计，完成多个独立数字波束对动态目标的自动跟踪。这方面的工程实现，国内外的研究近几年也才刚刚起步，公开发表的文献很少。本文总结了近两年几个工程项目中数字多波束球面相控阵系统对动态目标自跟踪问题的解决方案，希望促进国内在这方面研究工作的开展。

1 全空域球面相控阵测控系统概述

全空域球面相控阵测控系统天线阵面采用半球面加圆柱面布局的阵列天线，增加柱面的目的是为了改善低仰角时的增益，如图1(a)所示，以满足全空域覆盖的要求[2]。系统原理框图如图1(b)所示，系统由天线及射频前端、数字波束形成(Digital Beamforming，DBF)单元、波控单元以及综合基带等组成。系统采用数字多波束形成技术，充分利用了数字多波束形成的指向精度高、波束数目扩展灵活、系统易于升级等技术优点[2]。

(a)全空域球面相控阵测控系统天线示意图

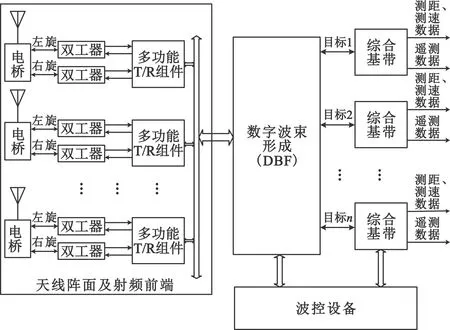
(b)全空域球面相控阵测控系统原理框图图1 全空域球面相控阵测控系统示意图

球面相控阵和传统的平面相控阵天线的工作原理是基本相同的，区别在于阵元的排列不是在平面上而是在曲面上，在分析计算其辐射特性时不能按照传统的平面阵列天线分析计算[2]。

2 角跟踪系统框架

全空域球面相控阵测控系统的角跟踪系统包括数字波束形成单元[2]、角跟踪接收机以及波控单元，如图2所示。

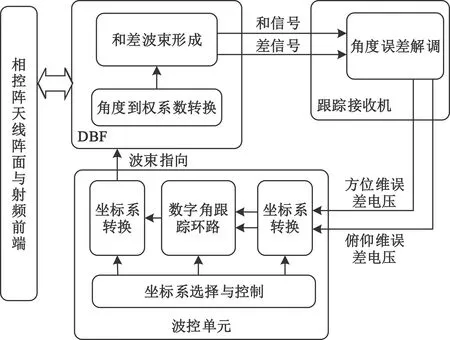
图2 角跟踪系统示意图

其中DBF由多级数字处理板卡实现，级数以及形成体量根据相控阵天线规模而定，其功能为接收射频前端相控阵天线阵面送下来的数字信号，根据波束指向形成和差数字波束。全空域球面相控阵测控系统的跟踪接收机与传统测控系统的跟踪接收机功能相同，通过解调和差信号，得到角误差电压，并送波控单元。波控单元可在波控计算机上由软件实现，其具体功能是根据任务情况进行坐标变换，接收跟踪接收机送来的角跟踪误差电压，再通过数字角跟踪环路，最终得到对跟踪目标的波束指向，并送DBF。

2.1 DBF和差波束形成

与传统测控系统相同，在全空域球面相控阵测控系统中，也可采用单脉冲跟踪体制或者圆锥扫描角跟踪体制。由于全空域球面相控阵测控系统采用数字波束形成，因此在实现上与传统测控系统还是有所区别的。

2.1.1 单脉冲角跟踪技术

单脉冲是一种雷达测角技术，也叫作同时多波束技术，最早是为了克服波束转换技术[1]和圆锥扫描技术[1]在雷达跟踪应用中跟踪精度不高而提出的。传统的单脉冲技术可分为幅度比较单脉冲、相位比较单脉冲与和差比较单脉冲。测控系统一般都采用和差比较单脉冲技术。

全空域球面相控阵测控系统单脉冲跟踪和差波束形成如图3所示，在DBF中，将任务目标指向激活的阵元进行A、B、C、D区域差阵列划分[1]。

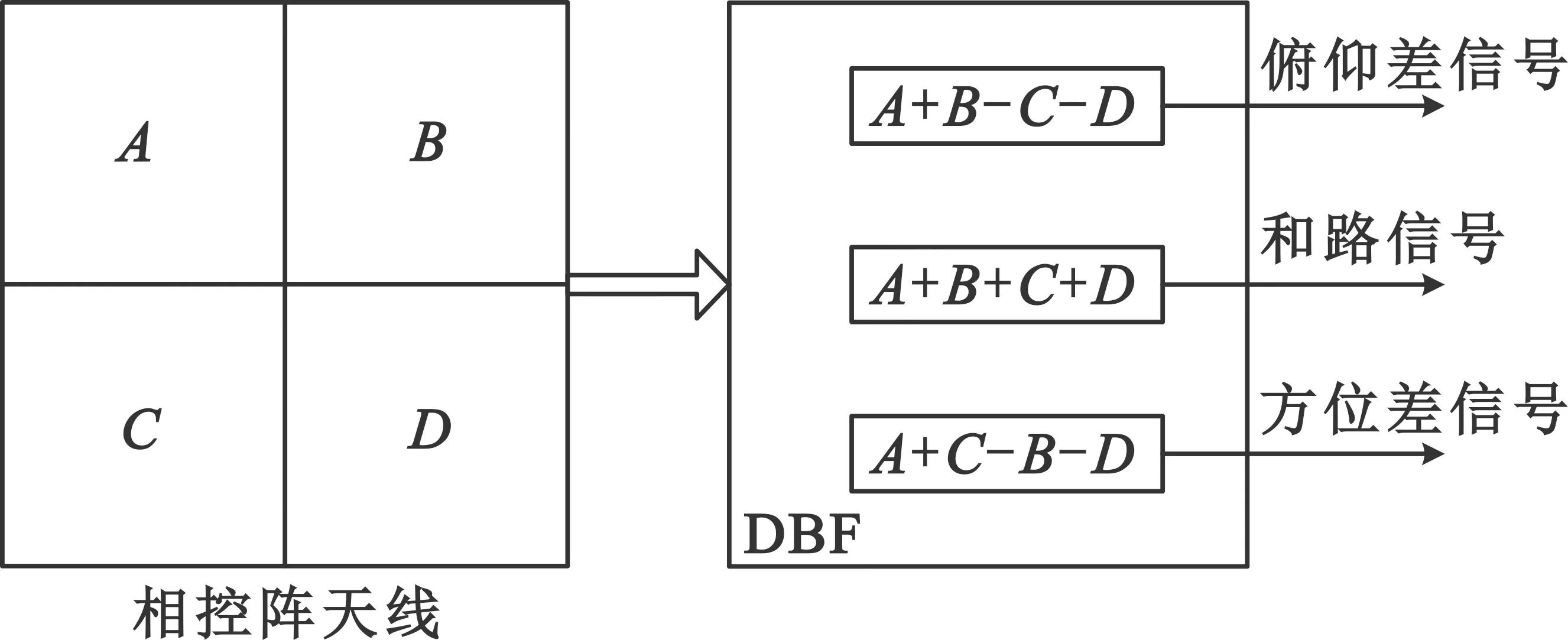
图3 相控阵和差波束形成原理

令(A+B)为接收通道的俯仰正相通道，则(C+D)为接收通道的俯仰负相通道。两个通道的相位中心距离为d，来波方向与指向角度之差为Δφ，则和信号为

(1)

俯仰差信号为

(2)

将和信号或差信号移相后相除，误差电压仅与指向偏差有关，即

Δu=tan(φ/2)=tan(πd/λsinΔφ)∝πd/λΔφ，

即给出了俯仰维的角误差电压公式，方位维推导过程与之相似。

根据波束指向与目标位置的角度差Δφ的不同，得到和/差方向图如图4所示。

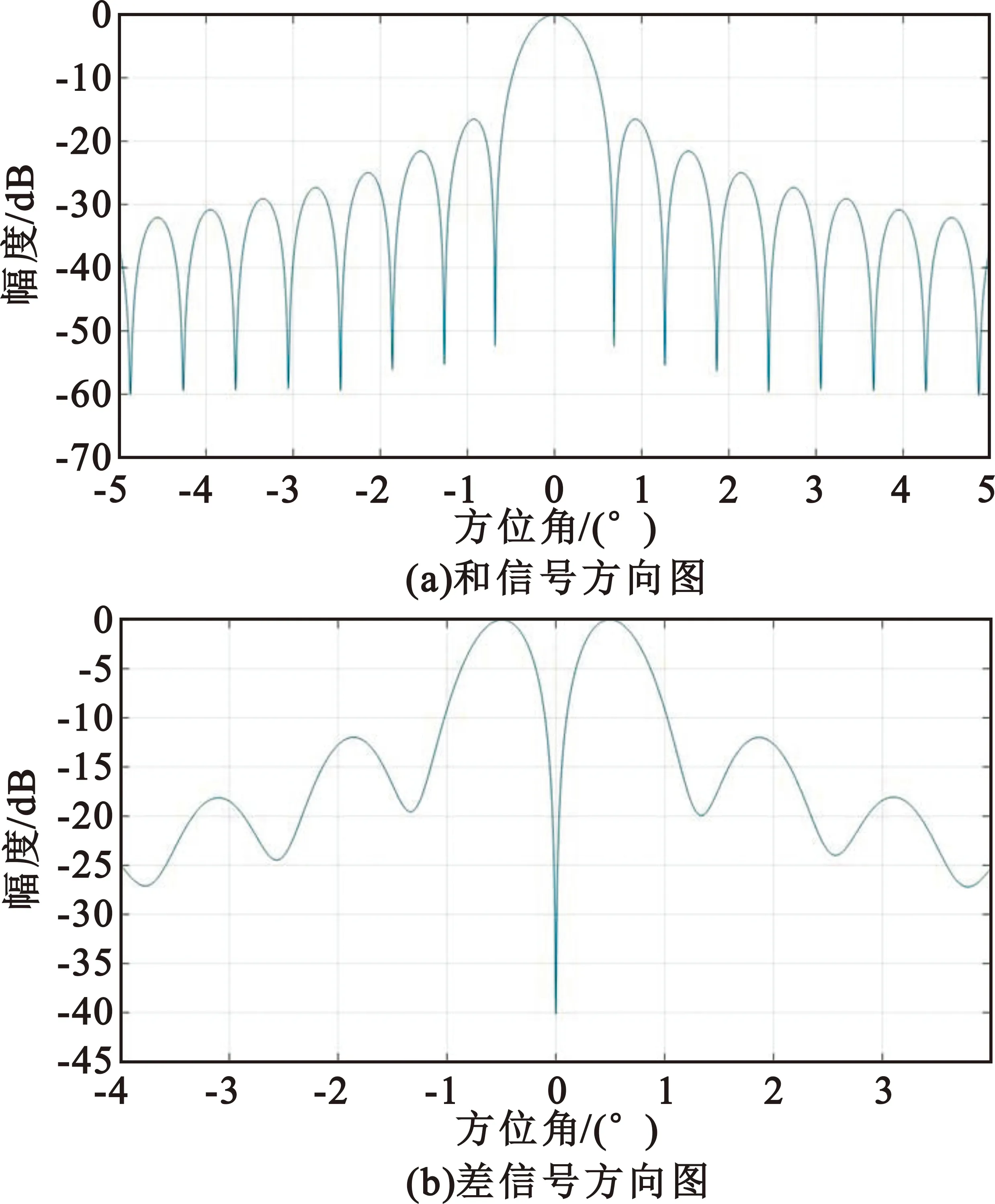
图4 天线和/差方向图

2.1.2 圆锥扫描角跟踪技术

圆锥扫描测角原理是将波束轴偏离反射器轴,并绕反射器轴旋转,以此来得到当前角误差。传统上可用旋转偏斜的喇叭、主反射器、副面、卡塞格伦副反射器、对称振子馈源等方式来进行圆锥扫描[6]。全空域球面相控阵测控系统由于采用数字波束形成技术，波束采用电扫方式，因此需要进行特殊设计才能实现圆锥扫描角跟踪技术。

全空域球面相控阵测控系统采用的圆锥电扫描方式如图5所示。与传统圆锥扫描一样，电扫描也是通过将扫描波束轴与理论波束轴偏开一个波束偏角δ，并且沿理论波束轴旋转。当理论波束轴指向目标即理论波束轴与目标轴重合(ε= 0)时，由于旋转的对称性，接收波束信号的幅度是一致的，可认为目标角跟踪差信号为0；当ε≠0(ε≤δ)，即理论波束轴没有向目标时，扫描波束在不同指向上得到的信号幅度就不相同了，而且这种差别与方位及俯仰角的偏差相关，即方位差信号与俯仰差信号是通过幅度调制在和信号上。与传统圆锥扫描不同的是，全空域球面相控阵测控系统波束的电扫描无法进行连续扫描，其扫描点是离散的，因此，在设计上采用在波束扫描环路按方位俯仰选择A、B、C、D四个对称的扫描点，如图5(b)所示，按一定时间间隔轮流指向这四个点。

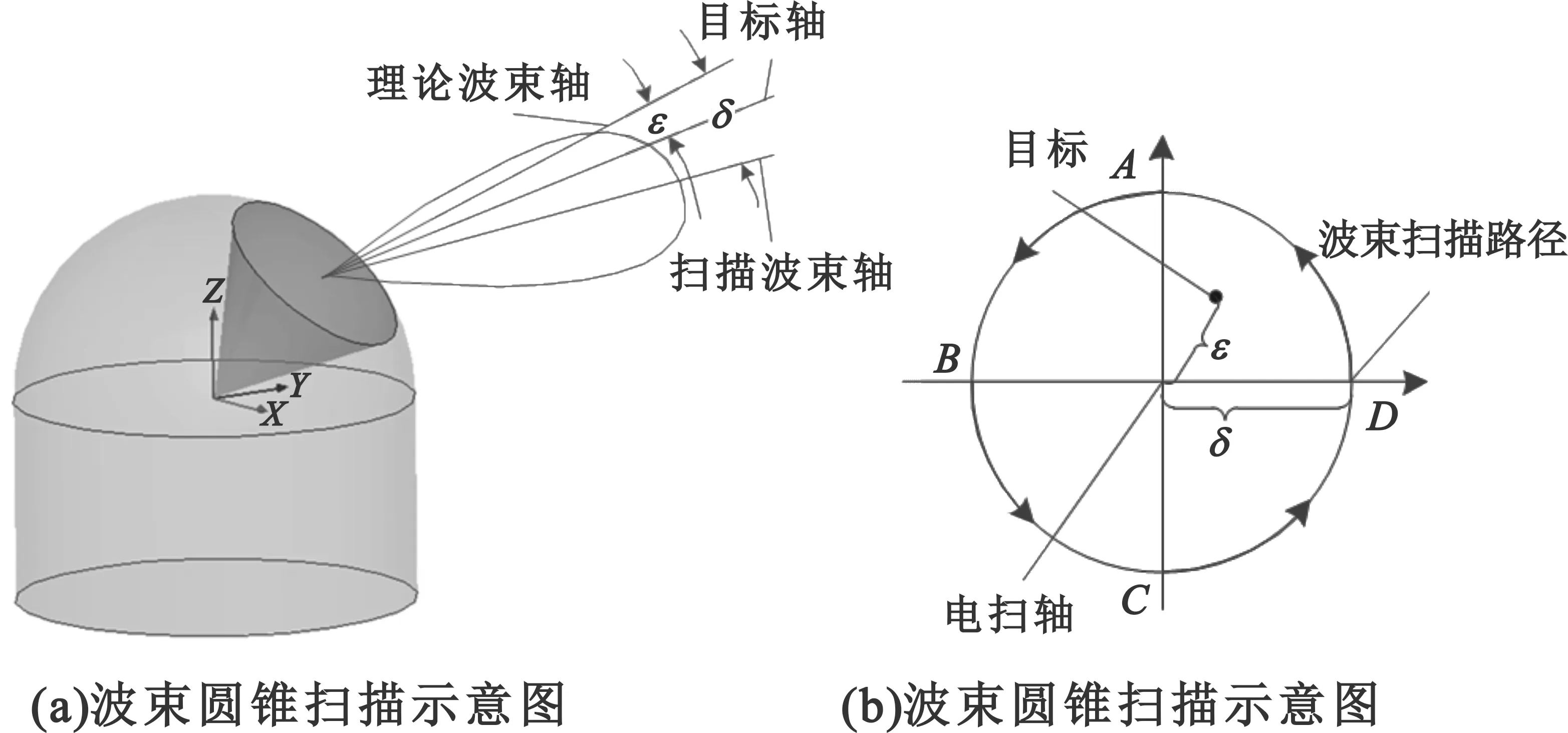
图5 相控阵天线圆锥扫描示意图

综合考虑硬件响应延迟时间及跟踪环路延迟时间等综合因素，取扫描间隔时间为5 ms，波束电扫描时序图如图6所示。

图6 相控阵天线圆锥扫时序图

根据图5，设波束轴与反射器轴线的夹角(波束偏角)为δ,跟踪误差为ε,在ε<<δ情况下,跟踪接收机的输出电压为[5]

(3)

从式(3)可知,跟踪接收机输出的信号为一幅度调制信号,要根据调制幅度和相位推算得到当前角误差信号,而方位和俯仰跟踪角误差可分别表示为[5]

(4)

最后一个问题是圆锥扫描的波束偏角δ的选取。文献[7]中对此进行了分析：δ越大，误差信号曲线的斜率Ks和越大，跟踪灵敏度就越高；δ越小，偏离天线电轴引起的信号功率损失Lk越小，接收信号的信噪比越高。所以，δ的选择应该兼顾角灵敏度和信噪比损失。文献[7]的结论是，选取归一化波束偏转角δ/θb为0.28，其中θb为天线半波束宽度。

2.2 跟踪接收机的设计

目前跟踪接收机技术成熟，有多种实现方式，根据输入的和差通道数可以分为单通道、双通道以及三通道跟踪接收机，航天测控领域应用比较多的是单脉冲体制的双通道跟踪接收机和圆锥扫描体制的单通道跟踪接收机。单脉冲单通道跟踪接收机多应用于卫星遥感侦察地面站，主要采用四相调制[8]或0/π调制方式[9-10]，通过中频数字化接收机[11]或直接利用单片机实现跟踪角误差信号的处理[12]。通常情况角误差信号的提取采用同步检波的方法，当接收宽带高信噪比的信号时，可截取部分带宽信号并采用更为简单的包络检波完成调幅信号解调，实现宽带信号的稳定跟踪[13]。

跟踪接收机从信号体制又可以分为标准TT&C跟踪接收机、扩频TT&C跟踪接收机以及数传跟踪接收机，这里仅简述单脉冲体制的标准TT&C跟踪接收机的设计方法。

标准TT&C双通道跟踪接收机主要是完成角误差信号的提取，得出俯仰和方位角误差信息送给天线伺服系统实现目标跟踪。全空域球面相控阵测控系统由波控单元实现波束的指向和跟踪，其原理框图如图7所示。

图7 标准TT&C双通道跟踪接收机原理框图

DBF输出的和差两路中频信号进入FPGA数字芯片送跟踪解调器模块，与和路信号鉴相后检测出方位和俯仰角误差信息，和路参考信号为移相后的环路数控振荡器 (Digital-Controlled Oscillator，DCO)输出信号，移相器与DCO一体化设计。自动增益控制(Automatic Gain Control,AGC)信号由和路产生，实现和路对差路信号幅度的归一化。

跟踪接收机解调出的方位及俯仰误差电压送波控角跟踪环路处理，由波控角跟踪环路转换成相应的方位及俯仰的角跟踪修正量，最终修正对动态目标的波控目标指向。

2.3 波控角跟踪环路设计

对于如何在相控阵天线中设计数字角跟踪环路,文献[3]中已经进行了详细分析，这里引用其结论。波控数字角跟踪环路的计算公式为

(5)

式中：G1、G2、K0为常量系数；θA/E(n)为当前目标方位/俯仰角；θA/E(n-1)为上一轮迭代计算所得目标方位/俯仰角；VA/E(n)为当前上报方位/俯仰误差电压；xA/E(n)、yA/E(n)为方位/俯仰环路计算的中间变量，跟踪开始时对其初始化。

文献[3]给出了对300 km轨道高度的低轨卫星跟踪特性的动态分析，在跟踪环路带宽选择为2BL=1 Hz的条件下，该设计的动态跟踪性能可以满足工程需要。

3 差阵列划分及过顶跟踪技术

3.1 传统差阵列划分及问题分析

按传统天线跟踪方式，球面阵天线差阵列划分是沿方位及俯仰方向划分，方位差阵列由通过Z轴的切面划分，并按照顺时针或逆时钟方向取极性；俯仰差阵列是按照与方位差阵列正交的方式划分，这种划分方式在天线高仰角时会出现差阵列划分旋转现象如图8所示，天线仰角越大，差阵列旋转角速度越大，在90°过顶时会出现差阵列划分在过顶点前后出现翻转180°现象。

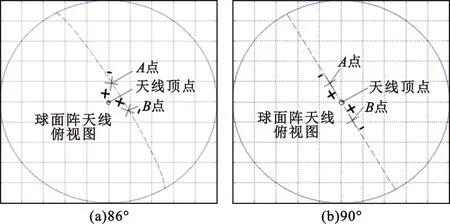
图8 过顶差阵列划分翻转示意图

根据上述情况，下面分析在天线或波束处于高仰角时，差阵列旋转对目标跟踪的影响。

3.1.1 建立数学模型

假设天线跟踪目标的角速度为Ω。根据上述分析，高仰角时由于差阵列旋转，等效于天线本身沿指向轴的一个轴向旋转。因此可建立模型如下：一个天线在圆周中心跟踪一个角速度为Ω的旋转目标，天线本身沿轴向旋转，旋转角速度为φ，如图9所示。

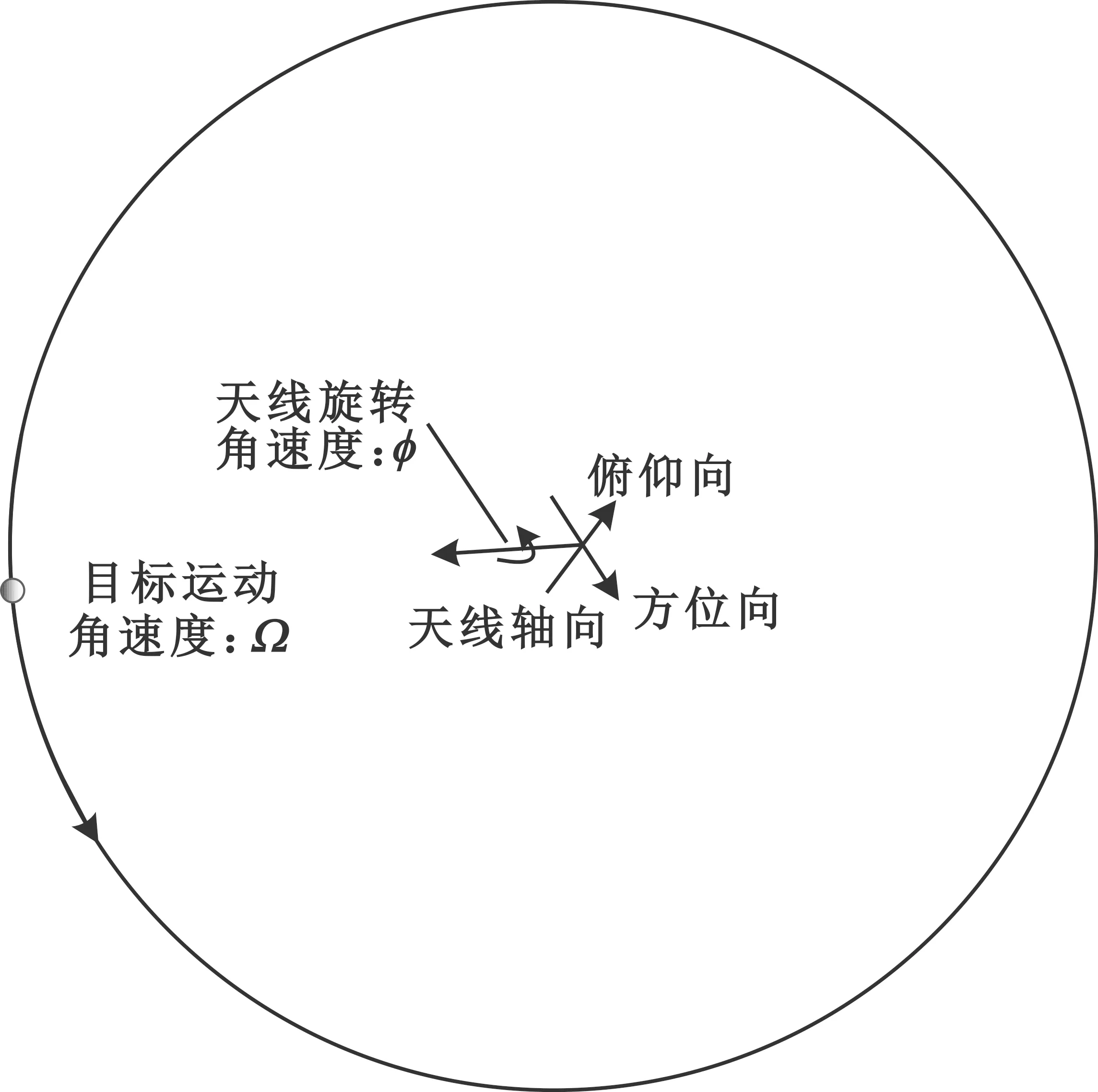
图9 90°过顶差阵列划分旋转示意图

设在时刻0时，天线方位与目标运动方向一致，则在时刻t天线方位方向角速度分量为Ωcosφt，天线俯仰方位角速度为Ωsinφt。

根据上述模型，在过顶点设目标在方位上的角速度为Ω,则在过顶点，天线在方位方向角速度分量为

Ωcosφt|t=0=Ω，

(6)

天线在俯仰方向角速度分量为

Ωsinφt|t=0=0 ,

(7)

天线在方位方向角加速度分量为

d(Ωcosφt)/dt|t=0=0 ，

(8)

天线在俯仰方向角加速度分量为

d(Ωsinφt)/dt|t=0=Ωφ。

(9)

3.1.2 波控角跟踪环路稳态误差分析

根据二阶环跟踪角加速度的稳态误差分析[14]，二阶环对角加速度的稳态误差为

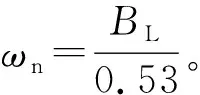
取跟踪环路带宽2BL=1 Hz，则

(10)

代入公式(9)即得在高仰角过顶点俯仰跟踪环路稳态误差为

θe俯仰=1.1236Ω2。

(11)

式中：Ω为目标在过顶点的方位角速度。

根据上述分析，过顶跟踪仰角越高，差阵列划分的旋转速度越快，极端情况下在90°仰角过顶时差阵列瞬间旋转180°，根据公式(11)，此时理论上俯仰角跟踪环路的误差为无穷大。因此，传统的球面差阵列划分方法在高仰角过顶跟踪情况下在会出现由于差阵列旋转而导致的附加跟踪误差，极端情况下会出现环路由于跟踪误差太大而导致丢失目标情况。因此，不能用传统的球面差阵列划分方法来处理高仰角过顶跟踪问题，必须另寻他径来解决全空域球面相控阵的高仰角过顶跟踪问题。

3.2 全空域球面相控阵过顶跟踪技术1

一种可以采用的过顶跟踪技术是高仰角限位的方法，即差阵列的划分在目标超过一定仰角时，划分差阵列的俯仰角保持在该门限角度上不再增加。根据公式(11)，可计算波控角跟踪环路的稳态误差，只要跟踪的稳态误差不超过天线的半波束宽度，即可保证波控角跟踪环路不会丢失目标。

假设天线半波束宽度为0.5°，根据公式(11)可计算出最大可容忍的过顶点方位角速度为5.05 °/s。这样就可以采用文献[4]中对飞行器轨道高度为300 km的低轨目标轨迹仿真的办法，得到门限俯仰角。如图10所示，卫星目标在73.5°仰角过顶时，方位角速度大于5 °/s。因此上述设定条件下，可以选择差阵列划分俯仰角门限为73.5°。通过上述分析可知,采用本方法可避免高仰角过顶跟踪目标时波控角跟踪环路丢失目标。

图10 卫星过顶动态仿真图

3.3 全空域球面相控阵过顶跟踪技术2

上面讨论了一种简单易行的球面相控阵过顶跟踪方式，但这种过顶跟踪方式在目标高仰角过顶跟踪时有两方面缺陷：一是这种方法存在跟踪的稳态误差，只能保证目标在高仰角过顶时波控角跟踪环路不丢失目标；二是在高仰角跟踪目标时由于差阵列划分在俯仰上不是以指向目标的轴为中心划分的，这样也会造成差波束的畸变，损失一些跟踪精度。为了解决全空域球面相控阵对高仰角过顶目标的波控角跟踪精度问题，文献[4]中讨论了另一种球面相控阵测控系统过顶跟踪技术，该技术是采用天线坐标系旋转的方式，其过顶跟踪设计包括坐标系旋转矢量的计算、自跟踪指向的计算与差阵列划分。采用这种方式可完全避免球面相控阵在高仰角过顶跟踪时的差阵列划分的旋转问题，具体分析见文献[4]，这里只引用其结论。

采用文献[4]的跟踪过顶设计，经过坐标旋转后可使得飞行器在整个测控跟踪过程保持在低仰角状态，极大地减小了测控目标的角跟踪动态。根据文献[4]仿真的结论，对轨道高度为300 km的低轨目标在不同仰角过顶时，采用坐标系旋转的方式可有效减少目标过顶时角跟踪的速度与加速度，在各个不同过顶点的最大角速度小于等于1.5 °/s,最大角加速度小于等于0.023 6 °/s，避免跟踪时由于角速度或角加速度过大导致的对目标跟踪不稳定甚至丢失目标的情况。

4 多目标跟踪技术与变口径跟踪技术

对于多目标跟踪技术来说，对每个独立跟踪的目标需要有独立的跟踪接收机以及波控单元，由于这两部分独立且相对简单，所以并不是限制系统规模的关键。真正限制系统规模的是DBF单元，其所能实现的下行波束数量决定了系统能同时跟踪目标的数量。全空域球面相控阵测控系统采用DBF技术，理论上数字波束形成技术可实现无限多波束通道，但实际上受数字处理芯片规模限制，其所能实现的接收通道数量是有限的，必须综合考虑系统需求与建设成本来设计跟踪目标数量。

在传统测控系统中小口径天线由于波束较宽常常用于辅助主天线对跟踪目标进行角度搜索和捕获。全空域球面相控阵测控系统由于采用DBF技术，可通过控制加权系数，按等效口径激活参与合成阵元的范围，因此很容易实现变口径收发信号，并且可自动实现小口径搜索及捕获目标、大口径接收目标信号。这些变口径跟踪技术具有广泛的应用前景。

5 结 论

本文概述了全空域球面相控阵测控通信系统角跟踪设计的各个方面，包含差波束形成技术、跟踪接收机设计以及角跟踪环路设计等。针对过顶跟踪时差阵列划分的局限性，本文提出了高仰角限位的方法，与坐标系旋转的方法相比虽然存在一定的角跟踪误差，但实践表明该方法简单易行，目标过顶时波控角跟踪环路工作稳定，因此在工程应用上具有现实意义。