一种抗扩频参数测量的低截获波形设计*
孙岩博
(中国西南电子技术研究所,成都 610036)
0 引 言
随着分布式作战、网络化协同作战、有人/无人协同等新型作战概念的提出和运用,除了对提升通信传输能力要求之外,更需要提升通信本身的射频隐身能力[1-2]。参数测量是通信侦察的核心,处于信号检测分离与类型识别之间,其中扩频参数测量是其重要环节,用于实现扩频信号伪码速率和扩频周期的估计,对于调制方式的识别、特定信号的搜索以及盲解调等具有重要的意义。
早期低截获波形采用直接序列扩频(Direct Sequence Spread Spectrum,DSSS)技术,通过降低传输信号瞬时功率谱密度,使信号淹没于噪声之下,迫使截获接收机难以获取足够多的能量,由此达到射频隐身的效果[3]。文献[4]采用多元低密度奇偶校验(Low Density Parity Check,LDPC)码作为信道编码,并结合自适应调制和DSSS技术来提高系统的低截获概率性能。文献[5]研究了非量化实值混沌直接序列扩频通信系统,利用其非恒包络特性,以降低被截获概率,但同时也带来严重的非线性失真问题。文献[6]采用混合扩频方式,将跳频技术与传统DSSS技术优势相结合,在低信噪比下隐蔽通信的同时有效克服远近效应。然而现有的低截获技术扩频体制单一,主要采用固定增益定码扩频体制,扩频信号特征具有较强的规律性,易被敌方侦测设备发现,难以满足未来体系作战的低截获需求[7-9]。为此,研究一种抗扩频参数测量的低截获波形具有重要的现实意义。
本文在兼容现有通信技术体制下,从抑制和消除通信信号中存在的可检测、可攻击统计特征的思路出发,通过引入随机过程对跳码扩频序列和扩频码速率进行随机化控制,使输出的码速率和扩频周期时间具有非平稳统计特征和非各态历经性质,以增强低截获波形抗扩频参数测量的能力。同时,辐射源扩频参数对于截获方是未知的,具有很强的不可预测和不可重构特征,可以实现真正意义上的物理层安全通信。
1 低截获波形方案
将信息安全的概念从传统的信息加密扩展至信号特征加密,由于通信系统协作式的工作特点,只要通信双方事先约定或在通信过程中重新约定,可以实现信号扩频特征的随机化控制,消除波形扩频特征的循环平稳性,使非合作对象的终端无法稳定测量。
1.1 发射方案
本文低截获波形以时隙为单位猝发通信。图1为低截获波形的时隙结构,主要由控制信息和业务信息组成。控制信息用于传输同步信息和通信波形特征参数指示信息,后者用于指引业务信息的处理方式。业务信息用于传输用户消息。为最大化扩频辐射特征的不确定性,同时降低截获接收机处理累积增益,本文采用跳码扩频方式,其不同扩频序列具备良好的互相关性。控制信息以事先约定的方式采用固定跳码图案进行扩频且不同时隙内控制信息的跳码图案是相同的。业务信息以通信过程中重新约定的方式引入混沌随机过程对不同扩频序列随机化控制实现对不同时隙内用户消息的动态扩频。每个时隙内相邻驻留时间所采用跳码扩频序列的扩频周期时间和扩频码速率是不同的。

图1 抗扩频参数测量的低截获波形时隙结构示意图
低截获波形时域表达式可表示为
x(t)=Ψ(s(t))ej(2πfct+θ),
(1)
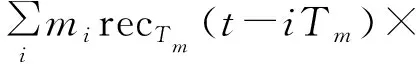
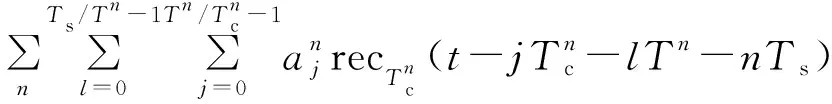
(2)
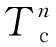
图2为低截获波形的发射结构。首先业务数据经基带调制、跳码扩频等处理得到业务信息已调信号,其中扩频序列通过Logistic映射的混沌随机过程,经量化处理后从跳码序列集合与扩频速率集合中随机生成。同时将业务信息已调信号采用的跳码序列和扩频速率作为波形特征参数指示信息用于控制信道传输,经过格式化模块将其与同步信息进行组帧和基带调制后,基于事先约定的跳码图案扩频处理得到控制信息已调信号。最后业务信息已调信号与控制信息已调信号进行复用组帧得到已调信号,最终已调信号经数字模拟转换器(Digital-to-Analog Converter,DAC)及上变频处理进行射频输出。
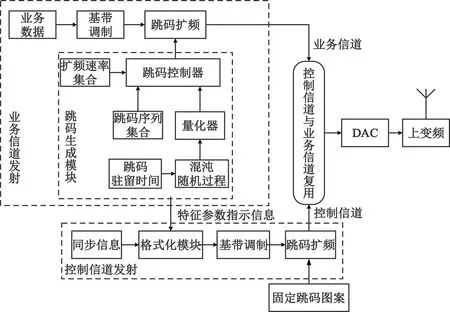
图2 抗扩频参数测量的低截获波形发射结构
Logistic映射是从Logistic方程演化来的,Logistic差分方程为
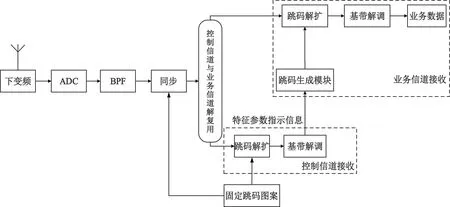
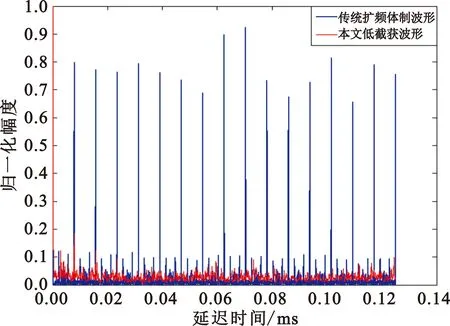
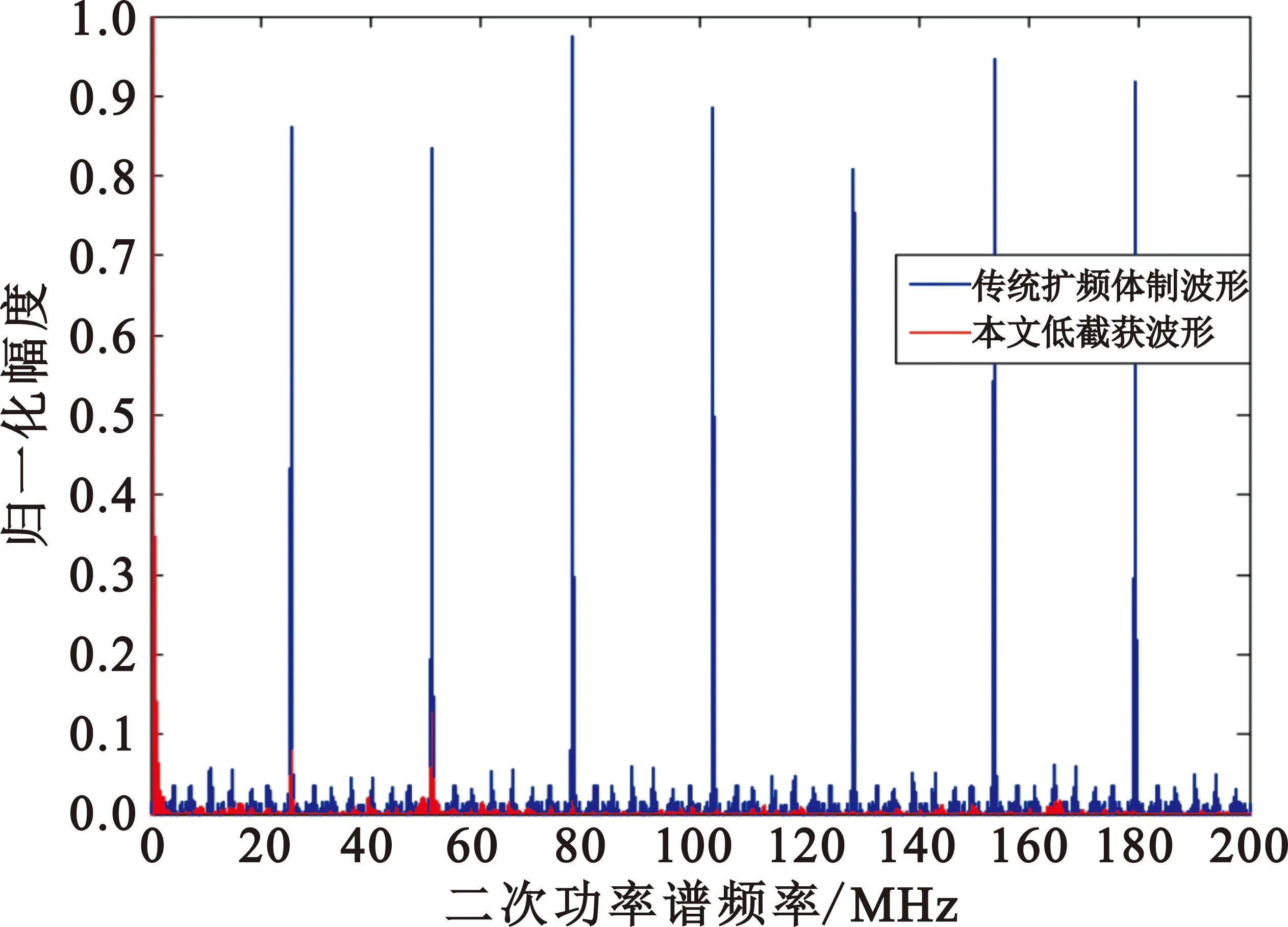
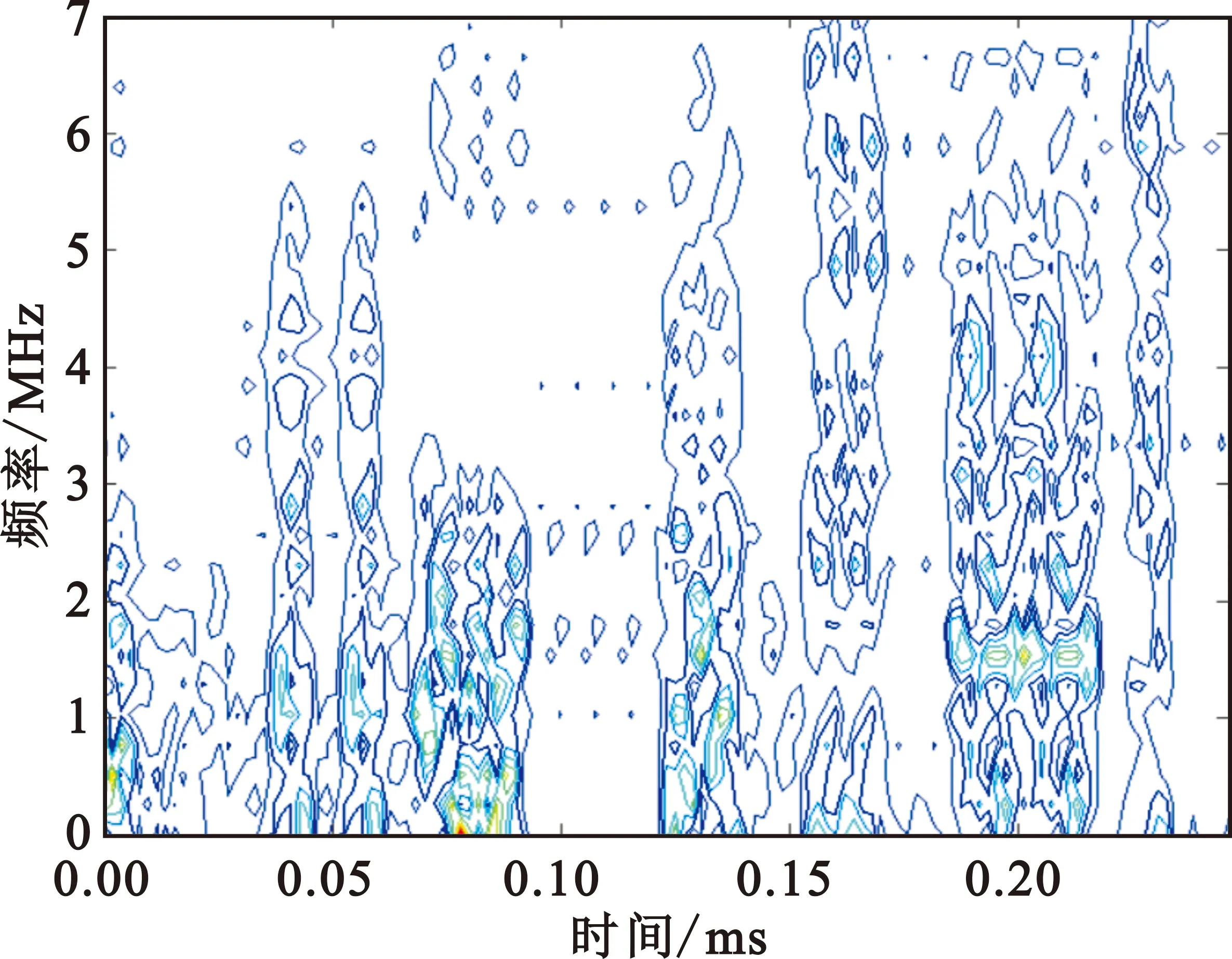
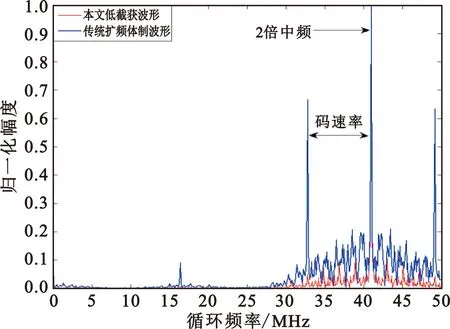
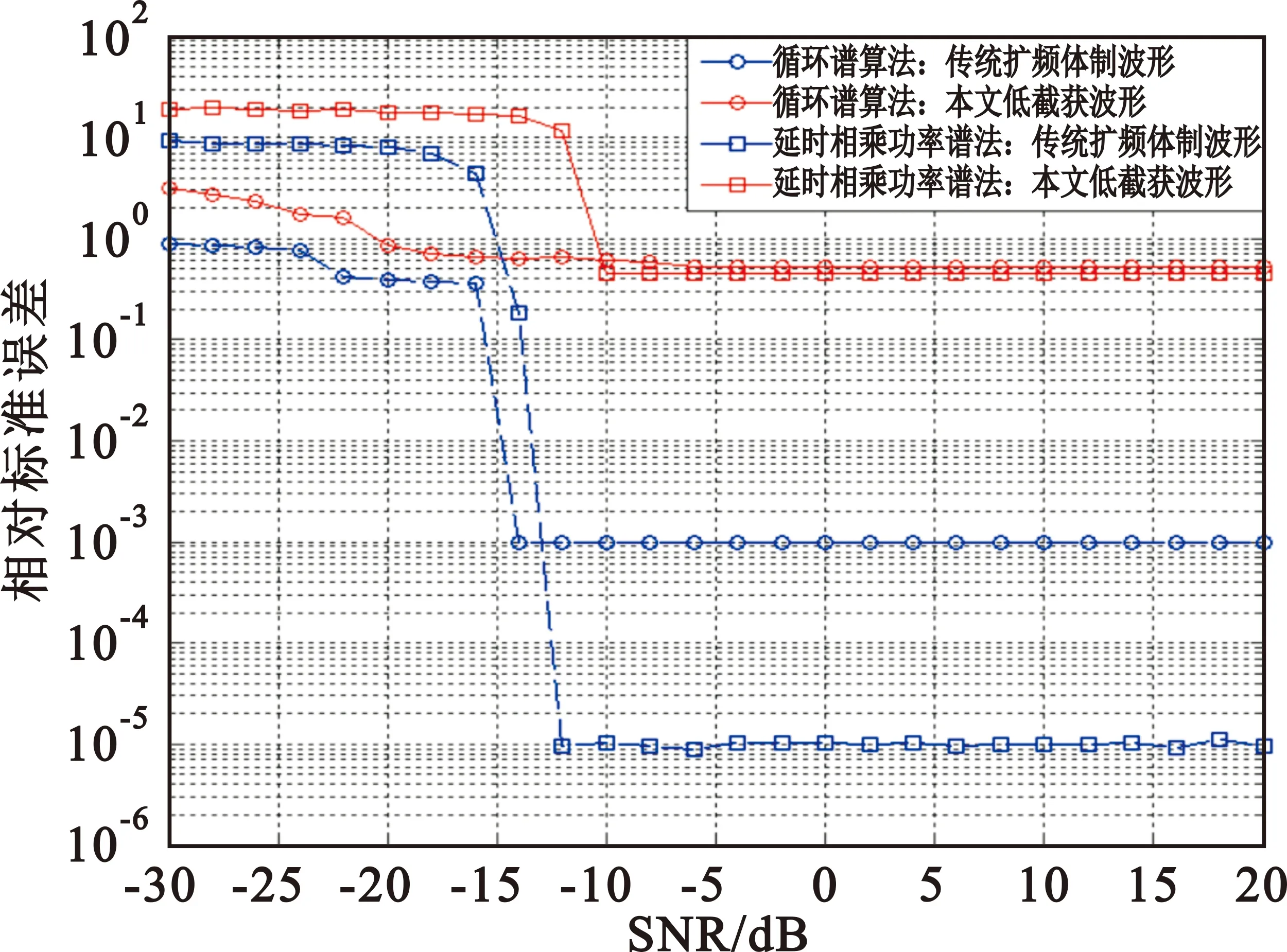
xk+1=uxk(1-xk),0 (3) 式中:xk是第k个混沌系统状态,u为映射的控制参数。采用非线性量化,每一个混沌序列实值都会产生一个量化后的跳码序列或扩频速率索引值i,具备运算量小且信息利用率高的特点。非线性量化方程为 (4) 式中:q是跳码序列集合或扩频速率集合样本数目。 低截获波形的接收结构如图3所示。接收端对接收信号进行下变频,模拟数字转换器(Analog-to-Digital Converter,ADC)和带通滤波器(Band-Pass Filter,BPF)处理输出已调信号,利用接收同步信息和本地产生的固定跳码图案扩频序列实现时间和载波同步,通过控制信道、业务信道解复用模块,将控制信息已调信号与业务信息已调信号进行分步处理:首先将控制信息已调信号根据事先约定的跳码图案依次进行解扩、解调等处理,恢复业务信息中波形特征参数指示信息,得到当前业务信息的扩频特征参数;然后跳码生成模块利用上述参数产生本地动态扩频序列,依次进行业务信息已调信号的跳码解扩、基带解调等处理恢复出用户信息。 图3 抗扩频参数测量的低截获波形接收结构 接收同步利用已知的同步信息实现定时同步和载波同步。定时同步用于搜索接收信号中同步信息的起始码相位。接收到的数字信号可表示为 (5) (6) (7) 按照中国2013胃肠胰神经内分泌肿瘤的分级标准[2],根据核分裂象计数和Ki67增殖指数将P-NENs分为NET G1级(核分裂数 ≤1个/10HPF,Ki67≤2%)、NET G2级(核分裂数2~20个/10HPF,Ki67为3%~20%)、NET G3级(核分裂数>20个/10HPF,Ki67>20%)、NEC G3级(核分裂数>20个/10HPF,Ki67>20%)。 载波同步是在定时同步的基础上,实现对多普勒频率和载波相位的准确估计。由于本文低截获通信系统采用猝发工作体制,需要载波同步快速锁定,为此可采用基于数据辅助的开环载波同步方法。由于同步信息是已知的,可通过本地再生的方法消除接收同步信息段内调制信号的影响。其中接收同步信息段信号可表示为 (8) 将r′(k)与本地同步信息复数域调制信号共轭相乘,得到 (9) (10) (11) (12) (13) 在电子对抗领域,敌侦收方对辐射源扩频参数的估计主要包括码速率和扩频周期。本节将对比分析所提出的低截获波形与传统扩频体制波形的参数估计性能。不失一般性,载波中频设为20.46 MHz,扩频速率集合为[2.048 MHz,4.096 MHz,8.192 MHz,16.384 MHz],跳码序列扩频增益集合为[16,32,64,128],调制方式为二进制相移键控(Binary Phase Shift Keying,BPSK)。 图4和图5分别对比了未加噪声下所提出的低截获波形与传统扩频体制波形的平均自相关二阶距和二次功率谱,其中传统扩频体制波形的扩频速率与扩频增益分别为8.192 MHz和64,所提出的低截获波形采用不同扩频速率与扩频增益组合的跳码扩频方式,且满足相邻驻留时间内跳码扩频序列的扩频周期时间和码速率是不同的,驻留时间设为62.5 μs。由图4可知,传统扩频体制波形的平均自相关二阶矩尖峰呈周期分布,其峰值间隔可准确估计出扩频周期时间;相反,所提出的低截获波形由于采用了变周期跳码扩频,不同驻留时间内的扩频序列具备良好的互相关特性,很大程度上降低了若干段信号二阶矩叠加后带来的累积增益,除了延时为零时刻的峰值外,导致其他峰值处幅值较低,同时也破坏了平均自相关二阶矩尖峰的周期性。与图4的现象相类似,由图5可知,传统扩频体制波形的二次功率谱在伪码周期整数倍处出现一系列的周期性尖峰脉冲,峰值间距即为扩频周期时间,而所提出的低截获波形显著抑制了二次功率谱可统计的周期特征。 图4 传统扩频体制波形和本文低截获波形的平均自相关二阶矩 图5 传统扩频体制波形和本文低截获波形的二次功率谱 采用二次功率谱算法和平均自相关二阶矩算法,图6分别对比了所提出的低截获波形与传统扩频体制波形的扩频周期时间估计精度。由图可知,随着信噪比(Signal-to-Noise Ratio,SNR)的增加,传统扩频体制波形的扩频周期时间估计精度提高,在高信噪比时,传统扩频体制波形在二次功率谱算法和平均自相关二阶矩算法下的扩频周期时间估计精度分别在约10-4和10-5数量级,而所提出的低截获波形由于其平均自相关二阶矩和二次功率谱不具备周期循环平稳性,同时也很大程度上降低了平均累积处理增益,导致扩频周期时间估计精度较差,在高信噪比下仍存在约0.6的相对稳态误差。 图6 扩频周期时间估计精度分析 由于码速率是影响信号时频特征的重要因素,在相同分析条件下,首先分析对比传统扩频体制波形与所提出的低截获波形的时频特征曲线,如图7所示。由图可知,传统扩频体制波形具备非常规律的时频特征;相反,所提出的低截获波形由于其相邻驻留时间内跳码扩频序列的码速率是不同的,导致其时频特征动态变化,不具备平稳的统计特征。同时,图8比较了未加噪声下传统扩频体制波形与所提出的低截获波形的循环谱特性。由图可知,传统扩频体制波形在零频时的循环谱切面表现出非常显著的载频特征和码速率特征,其中谱峰可准确估计2倍载频,谱峰和次峰间隔可准确估计码速率,而所提出的低截获波形很大程度上抑制了循环谱可统计的码速率特征。 (a)传统扩频体制波形的时频特征 (b)本文低截获波形的时频特征图7 传统扩频体制波形和本文低截获波形的时频特征 图8 零频时传统扩频体制波形和本文低截获波形的循环谱切面 由于截获信号往往具有比较低的信噪比,而延时相乘功率谱法[13]和循环谱算法[14]对噪声具有良好的抑制效果,可有效地估计扩频伪码速率。图9对比了上述两种算法下所提出的低截获波形与传统扩频体制波形的扩频码速率估计精度。由图可知,随着SNR的增加,传统扩频体制波形的码速率估计精度提高,在高信噪比时两种算法下的码速率估计相对标准误差分别在约10-3和10-5数量级,而所提出的低截获波形由于其具有非循环平稳统计特征,导致其码速率估计精度较差,在高信噪比下仍存在约0.5的相对稳态误差。 图9 码速率估计精度分析 为增强低截获波形抗扩频参数测量的能力,本文提出了一种抗扩频参数测量的低截获波形实现方案,通过引入随机过程对跳码扩频序列和码速率进行随机化控制,使输出的码速率和扩频周期时间具有非循环平稳统计特征和非各态历经性质。最后采用工程上常用的平均自相关二阶矩算法和二次功率谱算法以及循环谱算法和延时相乘功率谱法分别分析对比了传统扩频体制波形与所提出的低截获波形在扩频周期时间和码速率方面的测量精度。仿真结果表明,传统扩频体制波形在高信噪比下可准确估计扩频周期时间和码速率,其相对标准误差为10-3~10-5数量级;反之,所提出的低截获波形的扩频特征参量具有非循环平稳性,其扩频周期和码速率估计精度较差,在高信噪比下存在0.5~0.6的相对稳态误差,呈现出优越的抗扩频参数测量的能力,同时该技术也可与其他低截获技术相结合,实现多域特征参数的不可预测和不可重构,增强射频辐射源的低截获性能。1.2 接收方案
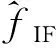
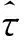
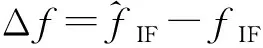
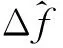
2 仿真与分析
2.1 扩频周期时间估计

2.2 码速率估计

3 结 论

