基于BP神经网络的OFDM系统信道估计*
纪勤文,朱春华
(1.粮食信息处理与控制教育部重点实验室,郑州450001;2.河南工业大学 信息科学与工程学院,郑州450001;3.河南省粮食光电探测和控制重点实验室,郑州450001)
0 引 言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统因其能够对抗多径效应、消除符号间干扰以及具有较高的频带利用率而成为无线通信的核心技术。信道估计是决定OFDM系统性能的关键技术之一,其中基于导频的信道估计应用最为广泛。传统的最小二乘(Least Square,LS)算法[1-2]实现简单、操作容易,并且不需要信道的先验统计信息,但其直接忽略了噪声的影响,因此会使导频位置的信道估计误差传播到数据位置的信道响应中[3]。线性最小均方误差(Linear Minimum Mean Square Error,LMMSE)算法在传统信道估计算法中的性能最好[4],但是其需要信道的先验统计信息以及矩阵的求逆运算,具有较高的计算复杂度。为了在较低计算复杂度条件下达到较好的信道估计性能,近年来,基于深度学习的信道估计方法成为研究的热点[5-7]。其基本思想是将频域变化的信道看作一个非线性的动态系统,可建模为自回归过程,这样OFDM系统的信道估计就转化为自回归系数的估计过程。
为了更深入地探究神经网络算法用于OFDM系统信道估计的性能,本文将建立OFDM信号数据采集平台以及基于反向传播(Back Propagation,BP)神经网络的OFDM系统信道估计模型,通过离线数据集对网络进行参数设置以及模型训练,并以此为基础对比分析网络参数和导频参数选择对OFDM系统信道估计性能的影响。本文利用神经网络的非线性映射,给出的基于BP神经网络的信道估计算法能够更好地从含有噪声的数据中学习到信道数据之间的映射关系,从而能估计出更加贴近实际信道特性的信道响应。
1 系统模型
基于BP神经网络的OFDM系统框图如图1所示。在发送端中每一个OFDM符号内都以一定的规则插入导频信号(块状导频或梳状导频等),本文所使用的是梳状导频,导频图样如图2所示。由于插入的导频序列和导频位置收发双方都是已知的,因此可在接收端分别提取导频信号和有用数据信号,并计算出导频处的信道响应,进而能够计算出有用数据处的信道响应并恢复发送信号[8]。

图1 基于BP神经网络的OFDM系统框图

图2中黑色圆圈代表导频数据,白色圆圈代表有用数据。在本文搭建的OFDM仿真系统中,使用一个OFDM符号为一帧数据,当一个OFDM符号内分配6个导频数据,并且前后各分配6个保护子载波(子载波总数为64,且图2未画出保护子载波)时,导频数据所在的子载波位置为[7,17,27,37,47,57]。
计算导频处的信道响应时,若采用LS算法,则计算公式为
(1)

为了评价神经网络算法的性能优劣,定义数据位置处信道响应真实值Hx为
(2)

(3)
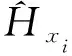
2 基于BP神经网络的信道估计流程
基于BP神经网络的信道估计整体框架如图3所示。
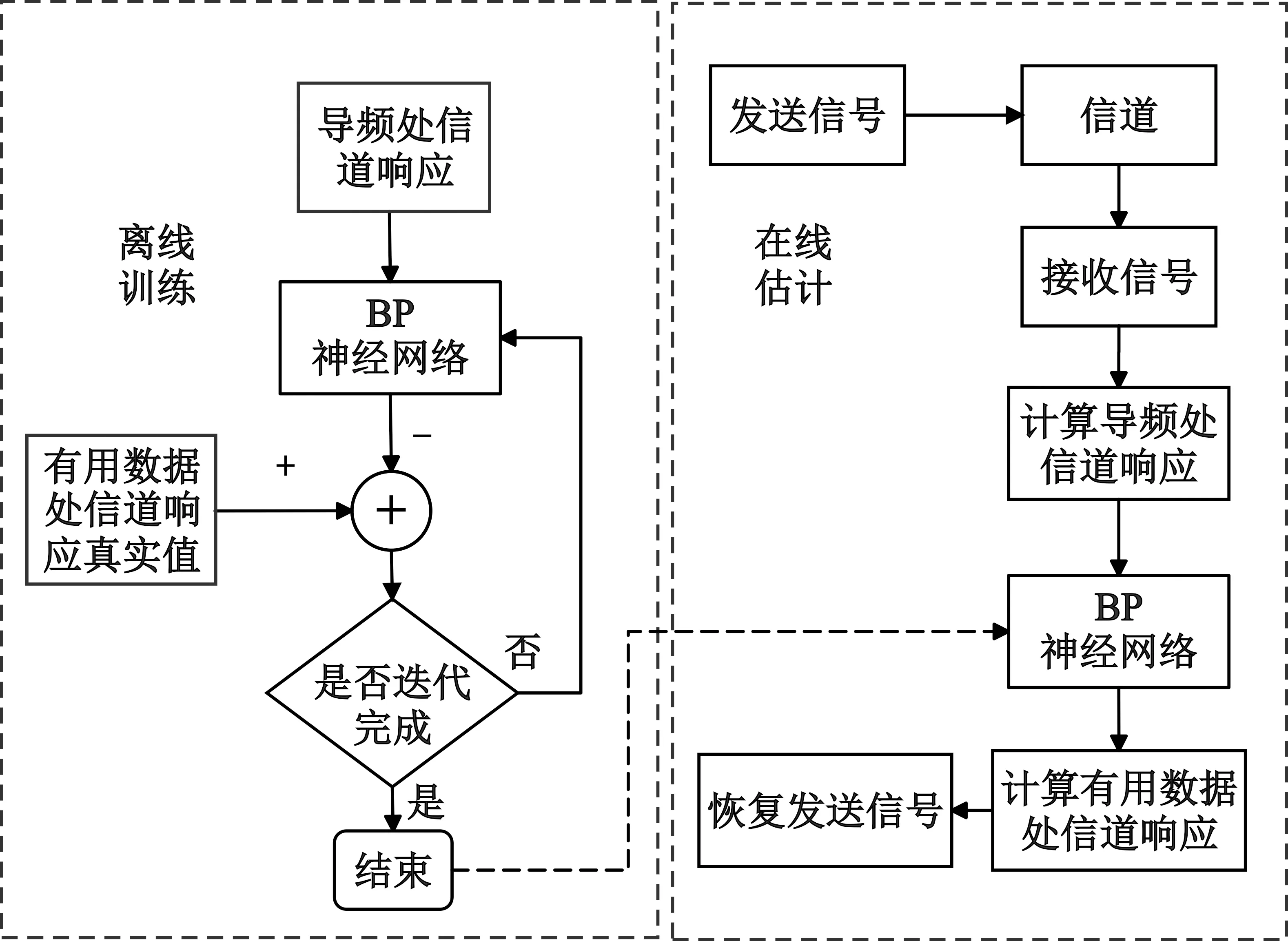
图3 基于BP神经网络的信道估计整体框架
图3中,本文提出的基于BP神经网络的信道估计主要分为两个阶段:离线训练和在线估计。在离线训练阶段,主要是使用大量先验的信道数据对神经网络进行训练,当所有样本输入完毕即完成一次迭代,通过多次不断地迭代,直至神经网络达到收敛状态,此时可保存网络的所有权重系数供在线估计阶段使用。在线估计阶段采用基于Simulink的OFDM系统仿真平台进行测试。首先在发送端生成包含有用数据和导频数据的基带信号,经过OFDM调制,并经过加性瑞利信道;在接收端,首先提取接收到的导频信号和有用数据信号,然后采用LS算法计算出所有OFDM符号的导频处信道响应,每次分别把一个OFDM符号内的导频处信道响应输入到训练好的基于BP神经网络的信道估计器中,可以得到一个OFDM符号内全部有用数据处的信道响应,据此可以恢复发送信号。
2.1 基于Simulink的OFDM信号采集平台设计
本文在离线训练阶段所使用的先验信道数据均是由Simulink仿真平台所得到的,基于Simulink的OFDM信号采集平台如图4所示。图4中,经过OFDM调制后的信号,先后经过瑞利信道和加性高斯白噪声(Additive white Gaussian noise,AWGN)信道,可设置不同的信噪比来模拟不同的信道环境。图中的Channel Estimation子系统主要是基于传统算法的信道估计,并完成相关数据的提取、分离和合成等。在采集训练数据时,主要收集的数据是图4中的Pilot_H和Target_H,其中Pilot_H表示的是导频处的信道响应,即式(1)中的Hp,而Target_H表示的是有用数据处信道响应真实值,即式(2)中的Hx。需要把不同信噪比条件下的Hp和Hx数据保存到本地的.csv文件中,以供离线训练时读取使用,且此处保存的均是把复数的实部和虚部分离之后的数据。

图4 基于Simulink的OFDM信号采集平台
2.2 BP神经网络系统结构
BP神经网络一般由输入层、隐藏层和输出层构成,通过增加隐藏层数量可提高网络的表示或识别能力,但同时也更容易出现泛化能力低下的问题。而经典的BP神经网络只有一个隐藏层,该类网络结构简单、运算复杂度低,常用于解决一些非复杂性问题。本文所使用的神经网络即由3层神经元结构组成,如图5所示。

图5 BP神经网络结构图
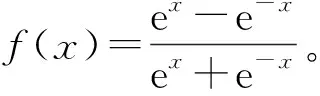
2.3 模型训练过程
由2.1节可知,基于Simulink的OFDM信号采集平台得到的不同信噪比条件下的Hp和Hx数据已经保存到本地的.csv文件中,它们作为训练数据使用。模型训练时,首先读取上述本地.csv文件中的数据,并把每一个样本中导频处信道响应的实部和虚部合成为一个列向量作为网络的输入值,将有用数据处信道响应真实值的实部和虚部也合成为一个列向量,作为网络的标签值。训练时需要确定损失函数和权系数更新算法。本文采用通用的均方误差损失函数和随机梯度下降算法,每输入一个样本数据就对网络的权重系数更新一次,直至网络达到收敛状态。此时可认为网络已经学习到了导频处信道响应和有用数据处信道响应之间的映射关系,也就是说,该网络能够基于导频位置的信道响应估计出有用数据处的信道响应,实现了基于导频的信道估计功能。经过上述模型训练过程并能够达到收敛状态的神经网络模型才可用于后续的在线信道估计。
3 仿真分析
为评估基于BP神经网络的信道估计器的性能,本节将对不同BP神经网络参数和导频参数下OFDM系统的信道估计BER和MSE性能进行仿真分析,所有的仿真都是在Matlab R2016a环境下进行,且没有考虑多普勒频移的影响。仿真中BP神经网络输入层和输出层神经元个数分别为12和92。对于离线训练阶段,训练集共有30 000个OFDM符号,在线估计使用的数据是由2.1节设计的基于Simulink的OFDM信号采集平台实时产生的,对某一固定的信噪比,都产生一定数量的OFDM符号,其总数据量是可调的,以下的仿真结果均是以每个信噪比产生1 000个OFDM符号进行实验所得。仿真中调制方式为QPSK,信道模型是EPA(Extended Pedestrian A model),噪声类型是AWGN,导频插入方式为梳状导频,其余OFDM系统参数如表1所示。
表1 仿真中的OFDM系统参数
3.1 学习率和隐藏层神经元个数对网络训练的影响
对于具有梯度下降的反向传播神经网络,学习率是训练神经网络的关键参数之一,它控制着每次迭代时权重系数更新的幅度大小,学习率过小会导致网络收敛速度慢,学习率过大会导致待优化参数在最优解附近振荡,不合适的学习率甚至会致使网络不收敛。学习率对网络训练性能的影响如图6所示,可以看出,当学习率从一个很小的值增大到某一个范围时,信道估计的MSE不再下降,此时对应的就是最优的学习率取值,图中对应的最优学习率为0.005;当学习率继续增大,网络有可能无法达到收敛状态,如图中学习率等于0.2时的情况。

图6 学习率对网络训练的影响
图7给出了不同隐藏层神经元个数对训练结果的影响,此时学习率为0.005。由图可见,随着隐藏层神经元个数的增加,网络训练收敛的性能差异不大。隐藏层神经元个数为5和10时,其对应的MSE曲线基本重合,考虑网络复杂度,可选择隐藏层神经元为5个。

图7 隐藏层神经元个数对网络训练的影响
3.2 网络学习率对信道估计性能的影响
根据3.1节在训练阶段寻求最优学习率的结果,测试不同学习率rate对在线信道估计BER性能的影响。这里同样选择一个OFDM符号内包含6个导频数据,其结果如图8所示。
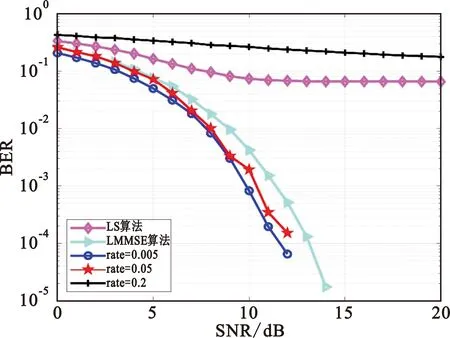
图8 不同学习率下的在线信道估计BER性能
图8给出了与图6相同的结论,在线信道估计阶段的BER对学习率的变化比较敏感,当学习率为0.005时可以达到最优的BER性能;当学习率为0.2时,信道估计的性能极差,这是因为在网络的训练阶段,该学习率下的网络并不能达到收敛状态。因此,在线估计阶段的信道估计性能取决于网络训练过程。但是学习率在一定范围内的变化并不会对在线信道估计的BER性能造成很大的影响,例如图8中的学习率为0.005和0.05时产生的BER曲线基本重合,即信道估计并没有因为学习率在一定范围内选择不同值而出现大幅度的性能差异。
3.3 信道估计算法对信道估计性能的影响
在上述最优网络参数下对信道估计模型进行训练并到收敛状态后,该神经网络模型就可用于在线信道估计。当选择一个OFDM符号内包含6个导频数据时,在线估计阶段基于BP神经网络(BP Neural Network,BPNN)算法的信道估计BER和MSE曲线分别如图9和图10中的Pilots=6所示,且图中对比了基于BP神经网络的信道估计算法与LS算法、LMMSE算法的信道估计性能差异。
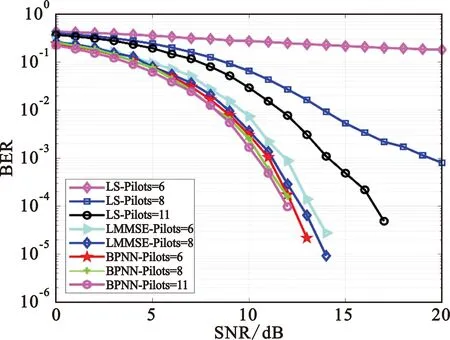
图9 导频数量对系统BER性能的影响

图10 导频数量对信道估计MSE性能的影响
由图9可见,随着SNR的增加,基于BPNN算法的信道估计BER性能优于传统的LS算法和LMMSE算法,且其随SNR变化呈现更快的下降趋势;在相同的误码率条件下,基于BPNN算法的信道估计所需要的SNR比传统LMMSE算法要少1 dB,这与文献[8]中所提出的基于深度学习的OFDM信道估计方法有着近似效果的性能提升,并且当SNR=13 dB时,本文使用的基于BPNN算法的信道估计的BER比LMMSE算法有10倍的改善。图10也显示出基于BPNN算法的信道估计相比传统算法的优势。引起上述结果的主要原因,一是LS算法忽略了噪声的影响,使得噪声引起的导频位置处信道估计误差传播到了数据位置处的信道响应估计值中,从而恶化了其信道估计性能;二是BP神经网络通过大量的先验信道数据对估计网络进行训练,该网络能够通过包含噪声的数据学习到信道数据的分布,拟合信道分布的过程即去噪的过程。
3.4 导频数量对信道估计性能的影响
一般来说,导频数量越多,信道估计的性能越好,但是大量的导频会占用一定的频带资源,导致频带利用率下降。因此,一般都希望用较少的导频达到信道估计的要求。
由图9和图10可见,随着导频数量的变化,传统LS信道估计方法的系统BER变化较大,呈现出BER性能随导频数量正比例变化的规律。但是,对基于BP神经网络的信道估计器来说,其系统BER和信道估计MSE对导频数量的变化不敏感,并且在相同导频数量下,基于BPNN算法的信道估计性能总是优于LMMSE算法。实际上当导频数量减少到0时,即在没有导频的情况下,LS算法是完全不能够进行信道估计的,但此时BP神经网络仍能端到端地恢复发送信号,只是此时信道响应就不会被显式地表达出来,而是网络把整个信道看成一个黑匣子,网络的输出直接就是基带调制信号,而不再是信道响应。因此,在具体应用时,只要有一定数量的导频即可,可结合网络训练和在线估计过程来确定。
3.5 算法复杂度分析
表2对比了LS算法、LMMSE算法、BPNN算法在完成一个OFDM符号信道估计的计算复杂度,其中复杂度以算法执行一次所需要乘法运算的次数为参考。

表2 计算复杂度比较
由表2可以看出,由于本文所给出的BPNN结构只有1层隐藏层,因此其计算复杂度和LS算法为同一个数量级。事实上BP神经网络的在线估计阶段只需要在每层进行简单的乘法和加法运算,其大部分复杂度主要体现在离线训练阶段的迭代过程。
4 结束语
本文系统研究了基于BP神经网络的OFDM系统信道估计的性能,完成了基于Simulink的OFDM系统训练数据采集、网络训练参数的优化选择以及导频设计等。研究发现,本文给出的基于BP神经网络的信道估计算法通过离线的信道数据学习到信道的特征,能够以LS算法相当的计算复杂度实现和LMMSE算法相似的信道估计性能。网络训练阶段的最优学习率、隐藏层神经元个数等参数可用于在线信道估计阶段,并且基于BP神经网络的信道估计算法只需要少量的导频,因而系统的频带利用率更高。值得说明的是,与卷积神经网络、循环神经网络、长短期记忆网络相比,本文所使用的BP神经网络由于采用的是梯度下降算法,因此其劣势是容易出现梯度消失的问题,从而会出现网络训练速度缓慢甚至停滞的现象,但是BP神经网络相比于其他网络来说实现更为简单。另外,BP神经网络的结构参数与应用场景以及前期离线训练阶段所使用的数据集有关,至今尚未有统一而完善的理论方法去推算出最优的网络结构,一般只能由经验所得。进一步探讨其他神经网络模型在OFDM系统信道估计中的应用将是未来的研究方向。

