高强钢筋含粗骨料超高性能混凝土梁抗弯承载力的正交分析

唐佳军，安思龙，胡 杰，王 坦，李九阳

(长春工程学院土木工程学院，吉林 长春 130012)

含粗骨料超高性能混凝土(Ultra high performance concrete with coarse aggregate，UHPC-CA)和活性粉末混凝土(Reactive powder concrete，RPC)同属于超高性能混凝土(Ultra high performance concrete，UHPC)范畴[1-3]。 以往研究表明，不同目标温度环境下，UHPC-CA的残余抗压强度均高于RPC，粗骨料对UHPC残余抗压强度的提高具有显著作用[4]；不同含湿量条件下，UHPC-CA的爆裂温度范围较RPC小、持续时间较短、爆裂声响次数较少、试件内部温度差较低、90 mm尺寸的碎块累计筛余较大，UHPCCA的高温爆裂性能高于RPC，粗骨料有利于提升UHPC的高温爆裂性能[5]。

高强钢筋的使用能够节约工程总用钢量，以HRB400 级代替HRB335 级和以HRB500 级代替HRB400 级时的省钢率分别为12% ～14%、5% ～7%[6]。 将高强钢筋和UHPC-CA结合，可充分发挥二者优良的力学特性。 孙涛[7]设计拉拔试验，分析了钢筋黏结长度、保护层厚度和养护龄期对HRB400 级钢筋与UHPC-CA黏结性能的作用规律。结果表明:当黏结长度由4 D(D为钢筋直径)加大至6 D时，极限黏结应力τu减小5.95 MPa；当保护层由10 mm增加至35 mm时，τu增大6.64 MPa；当龄期由7 d(d 表示天数)增加至28 d 时，τu增大10.46 MPa。 邓宗才等[8]对6 组HRB500 级钢筋UHPC-CA梁(参数为配筋率和截面形式)实施了抗弯性能测试，试验发现高强钢筋UHPC-CA梁的加载经历与普通混凝土梁类似，但钢纤维的存在显著提高了UHPC-CA梁的刚度。 徐海宾等[9]进行了高强钢筋UHPC-CA连续梁弯矩的调幅研究，基于非线性理论分析计算了承载能力极限状态和正常使用极限状态下的弯矩调幅系数。 金凌志等[10]分析了有无腹筋与剪跨比λ对高强钢筋UHPC-CA梁抗剪性能的影响。 结果表明:对于无腹筋梁，当λ为1.00、2.25、3.00 时，高强钢筋UHPC-CA梁的破坏形式分别为斜压、剪压和斜拉破坏；对于有腹筋梁，梁的破坏形式为剪压破坏(λ为1.00、2.25)和斜拉破坏(λ为3.0)；随着λ的增大，高强钢筋UHPCCA梁的斜裂缝倾角与抗剪承载力均逐渐减小。

考虑到目前有关高强钢筋UHPC-CA梁受力性能的研究较少，本文以钢筋等级、钢筋直径、截面有效高度和混凝土强度等级为因素，高强钢筋UHPCCA梁的抗弯承载力为指标，分析指标随各因素的变化规律、各因素对指标的影响大小与显著性程度，为高强钢筋UHPC-CA梁的理论研究提供参考。

1 试验概况

1.1 试验方案设计

设计L9(34)正交试验方案，选取4 个因素:钢筋级别(因素A)、钢筋直径(因素B)、截面有效高度(因素C)和混凝土强度等级(因素D)。 因素A包括HRB400 级、HRB500 级和HRB600 级钢筋3 个水平；因素B的水平有14、16、18 mm 3 类；截面高度选取180、200、220 mm 3 种，假定保护层厚度是20 mm，箍筋直径是10 mm，则对应因素C的水平值为143、162、181 mm；因素D的3 个水平包括C130、C150 和C180，其中C130UHPC-CA的强度数据源自杨娟[11]，C150UHPC-CA选自陈飞翔等[12]的论文，C180UHPC-CA则是李仕根[13]文中的数据。 试验因素与水平见表1，试验方案设计见表2。

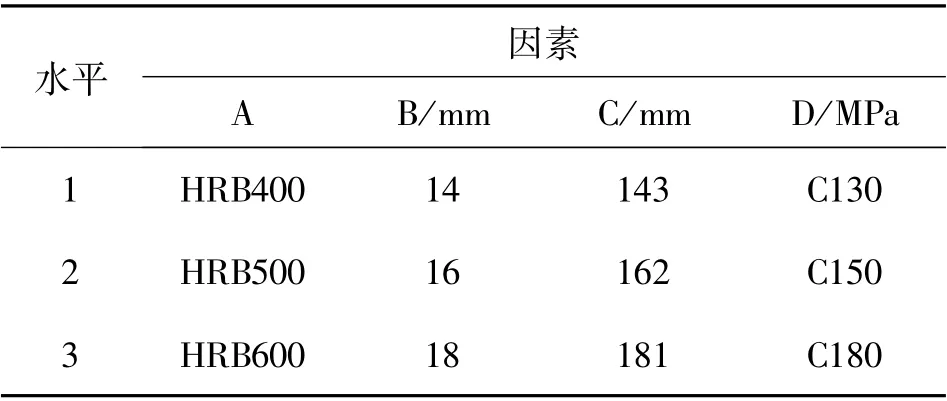
表1 试验因素与水平

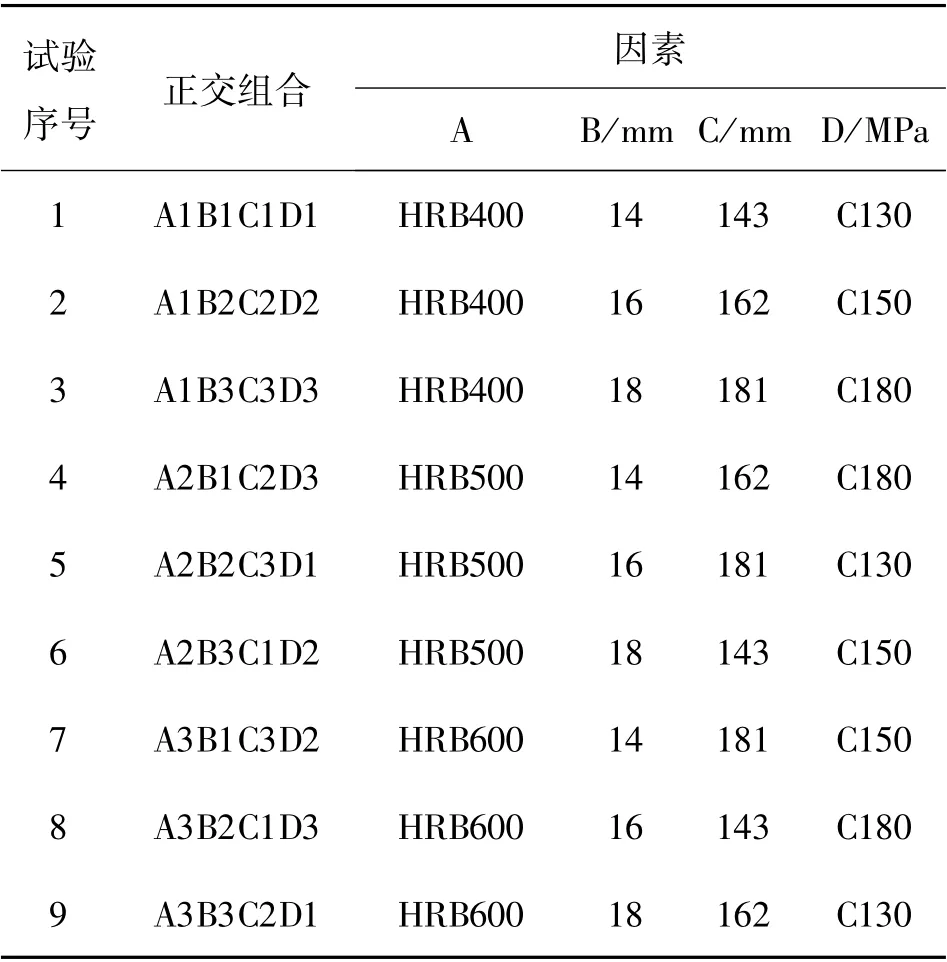
表2 试验方案设计

1.2 试件设计

图1 可见梁试件的截面大小与配筋构造。 除了以上提及到的钢筋信息与截面高度等，由图还可以看出，梁的截面宽度为120 mm，纵向受拉钢筋为2根，箍筋选用ϕ10＠100 的双肢箍，架立筋直径是10 mm。

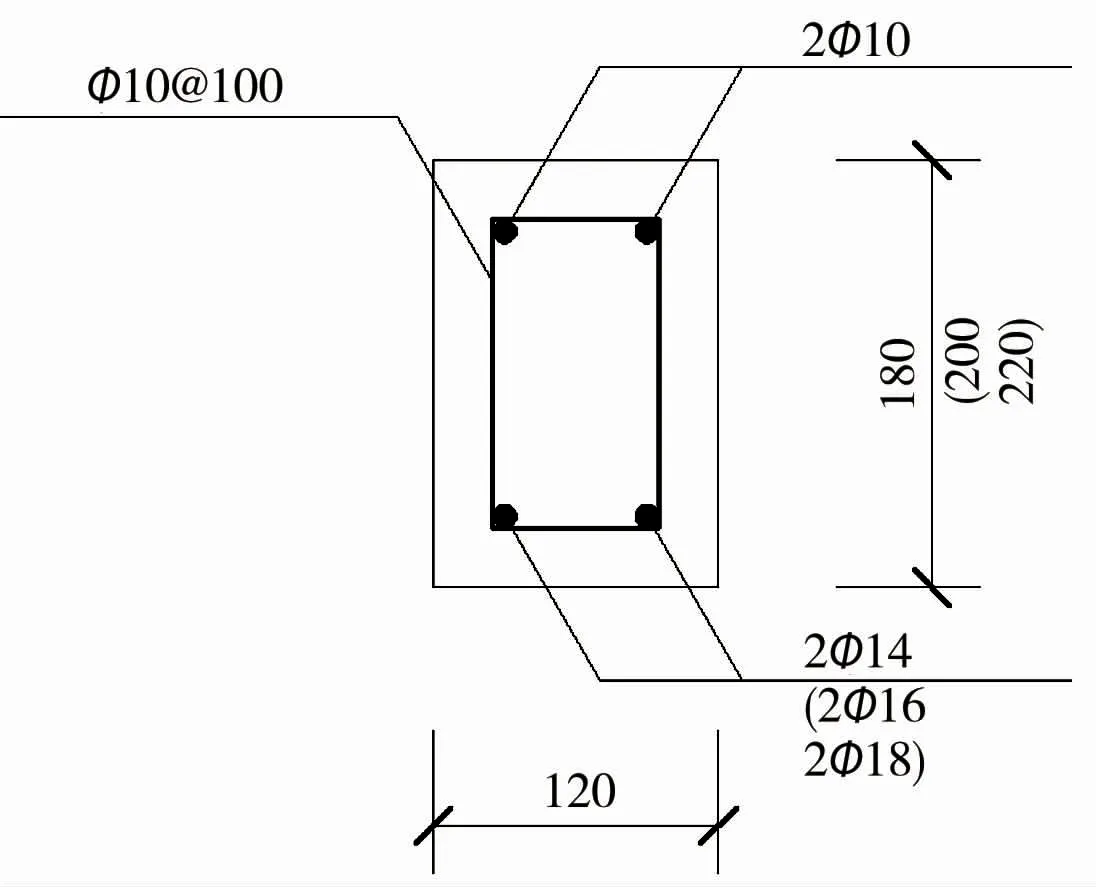
图1 梁试件的截面大小与配筋构造(mm)

1.3 抗弯承载力的计算

由于UHPC-CA的抗拉强度较高，因此在进行高强钢筋UHPC-CA梁正截面抗弯承载力的计算时，需要考虑受拉区混凝土的贡献。 本研究采用郑文忠等[14]的计算方法:

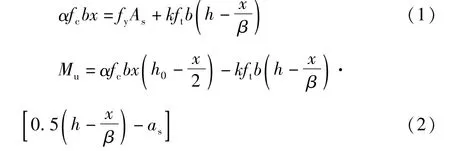
式中 Mu——高强钢筋UHPC-CA梁的正截面抗弯承载力；fc——UHPC-CA的轴心抗压强度设计值；ft——UHPC-CA的轴心抗拉强度设计值；fy——纵筋抗拉强度设计值；As——纵向受拉钢筋截面面积；as——纵筋合力点到截面受拉边缘的距离；α、β——受压区等效矩形应力图系数，α=0.9，β =0.77；k——受拉区等效矩形应力图系数，k=0.25；x——受压区高度；b——截面宽度；h——截面高度；h0——截面有效高度。

2 试验结果分析

表3 示出了各试验组高强钢筋UHPC-CA梁受弯承载力的试验计算结果。

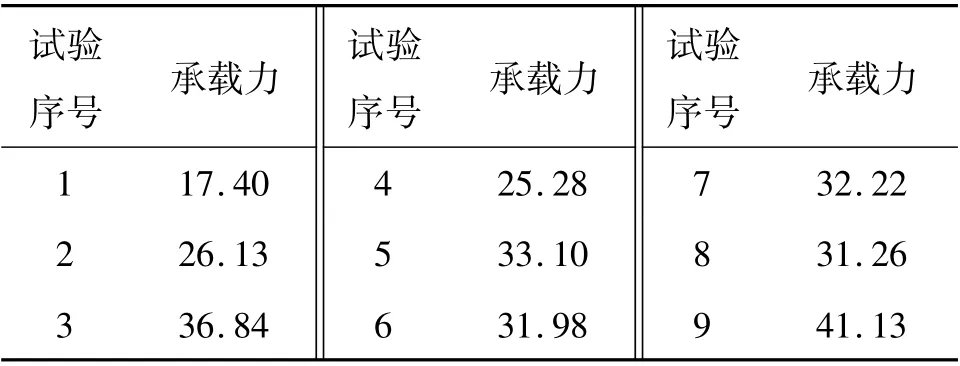
表3 试验计算结果单位:kN/m

2.1 直观分析

分析表3 可知，第9 组梁试件的抗弯承载力最大，为41.13 kN·m，此时的正交组合为A3B3C2D1，即钢筋等级是HRB600 级、钢筋直径是18 mm、截面有效高度是162 mm、UHPC-CA强度等级是C130；第1组试件梁的抗弯承载力最低，为17.40 kN·m，此时的正交组合为A1B1C1D1，即钢筋等级是HRB400级，钢筋直径是14 mm，截面有效高度是143 mm，UHPC-CA强度等级是C130。 对比分析可知，对于C130UHPC-CA，同时提高其钢筋等级(由HRB400级至HRB600 级)、钢筋直径(14 ～18 mm)和截面有效高度(143 ～162 mm)，梁抗弯承载力增加了23.73 kN·m，增幅为136.4%，增长显著。

2.2 极差分析

表4 为钢筋等级、钢筋直径、截面有效高度和UHPC-CA强度等级4 个因素对高强钢筋UHPC-CA梁抗弯承载力影响的极差值。 可以看出，因素A、B、C、D对应的极差值分别为8.08、11.68、7.18 和1.02，各因素对抗弯承载力的影响由大到小依次为B＞A＞C＞D，即钢筋直径＞钢筋等级＞截面有效高度＞UHPC-CA强度等级。

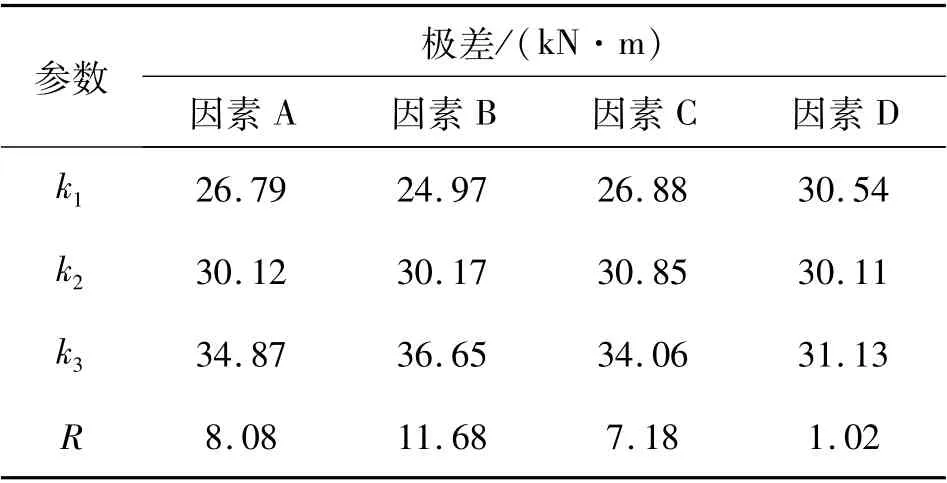
表4 抗弯承载力的极差分析

2.3 因素指标分析

为了得到研究指标随因素水平的变化规律，将表4 中各因素水平下抗弯承载力的平均值绘制成点图，见图2。

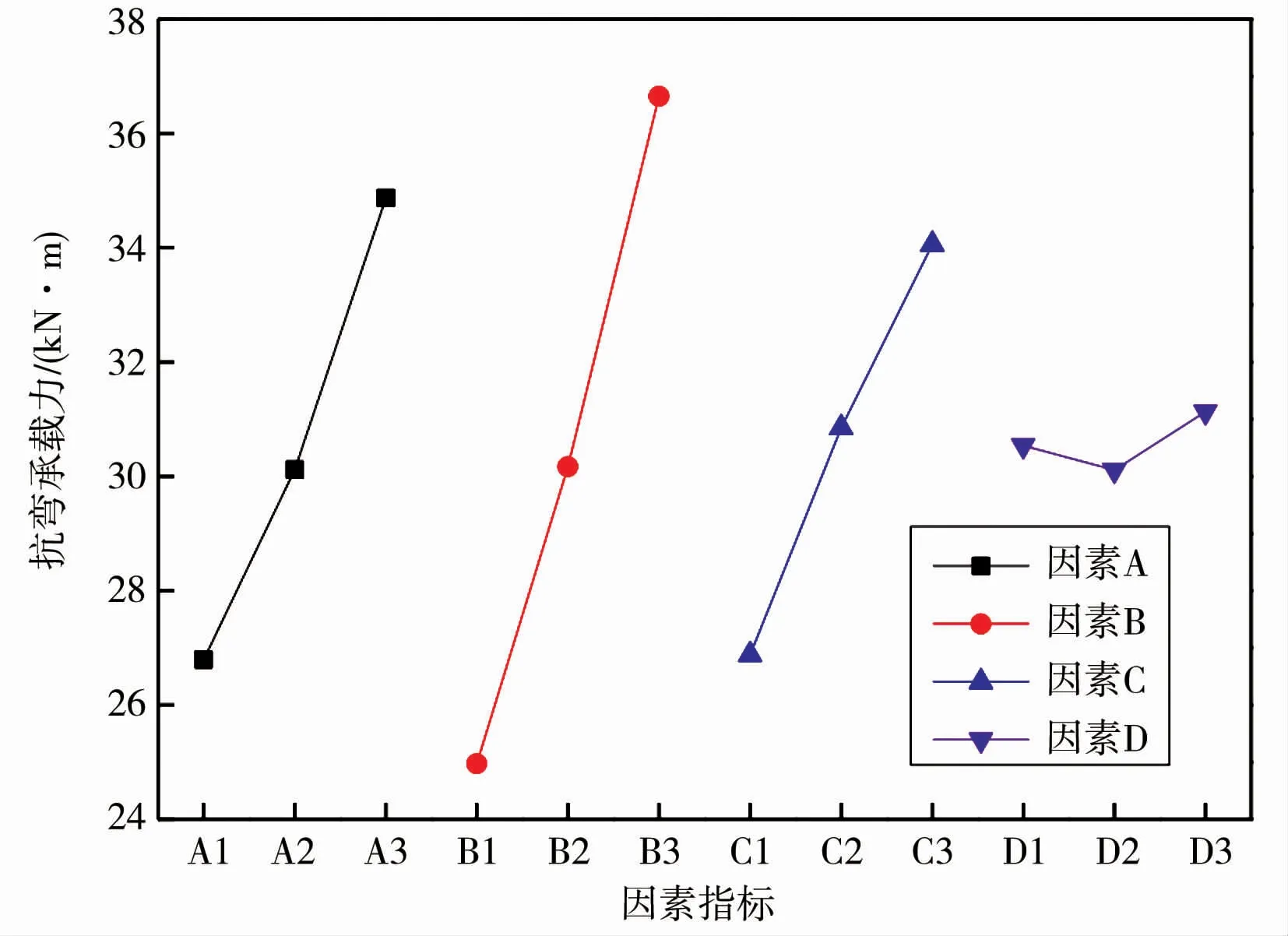
图2 抗弯承载力随因素水平的变化

由图2 可知，随着因素A、B、C的增长，高强钢筋UHPC-CA梁的抗弯承载力均逐渐增加；随着因素D的增加，抗弯承载力先略有降低后小幅增长。当钢筋等级由HRB400 级变化至HRB600 级时，抗弯承载力提升了30.2%；当钢筋直径从14 mm增加到18 mm时，抗弯承载力升高了46.8%；当截面有效高度从143 mm增长至162 mm时，抗弯承载力增大了26.7%。 当UHPC-CA强度等级由C130 增强至C150 时，抗弯承载力降低了1.4%；由C150 增强至C180 时，抗弯承载力升高了3.4%；C180 UHPCCA对应的抗弯承载力较C130 UHPC-CA增加了1.9%。 可见，UHPC-CA强度等级的提升对梁抗弯承载力的增强作用并不明显，而钢筋等级、钢筋直径和截面有效高度的增加对梁抗弯承载力的增强作用较为显著。 限于本研究中选取的UHPC-CA强度等级的数据较少，高强钢筋UHPC-CA梁抗弯承载力随UHPC-CA强度等级的变化规律需要进一步研究。

2.4 矩阵分析

为了计算各因素水平对抗弯承载力的影响权重，对研究指标进行矩阵分析。 将表4 中极差分析计算结果按照文献[15]中的方法以矩阵的形式编写并输入MATLAB软件窗口运行，将最终矩阵计算所得结果列于表5。

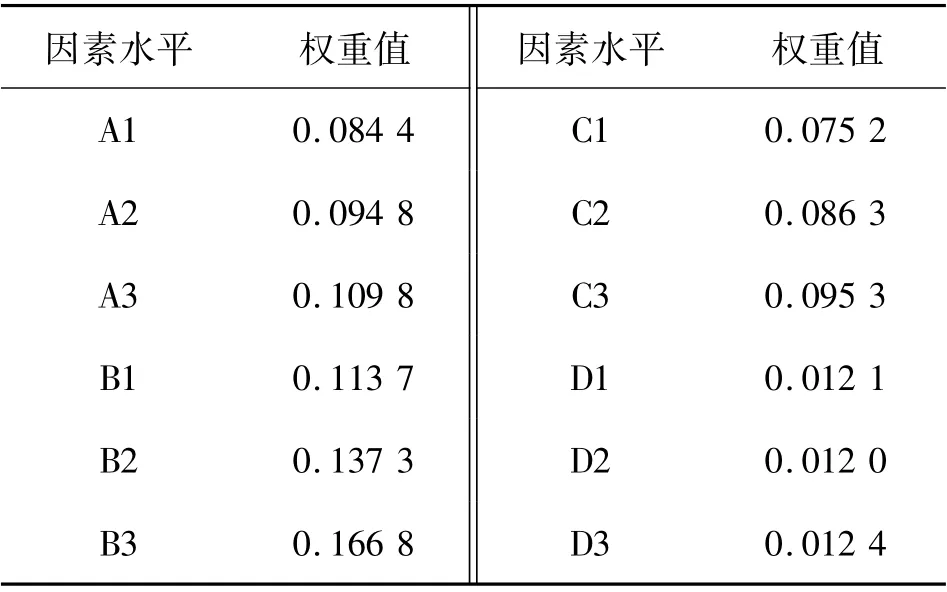
表5 抗弯承载力的矩阵分析

由表5 可知，在钢筋级别的3 个水平中，A3 对抗弯承载力的影响权重最大，权重值为0.109 8；在钢筋直径的3 个水平中，B3 的影响权重最大，值为0.166 8；在截面有效高度的3 个水平中，C3 的影响权重最大，值为0.095 3；在UHPC-CA强度等级的3个水平中，D3 的影响权重最大，值为0.012 4。 因此组合为A3B3C3D3，即钢筋等级是HRB600 级，钢筋直径是18 mm，截面有效高度是181 mm，UHPC-CA强度等级是C180 时，高强钢筋UHPC-CA梁的抗弯承载力将达到最大值。

2.5 方差分析

为了得到各因素对抗弯承载力作用的显著性程度，对研究指标进行方差分析，抗弯承载力的方差分析结果见表6。 由表可知，因素A、B、C对抗弯承载力均存在显著影响，因素D不存在显著影响。 其中钢筋直径为重要显著因子，对抗弯承载力的影响最大；钢筋级别和截面有效高度为一般显著因子，钢筋级别对抗弯承载力的影响高于截面有效高度；混凝土强度等级的影响最小。 可见，以上分析结果与极差分析相符合。

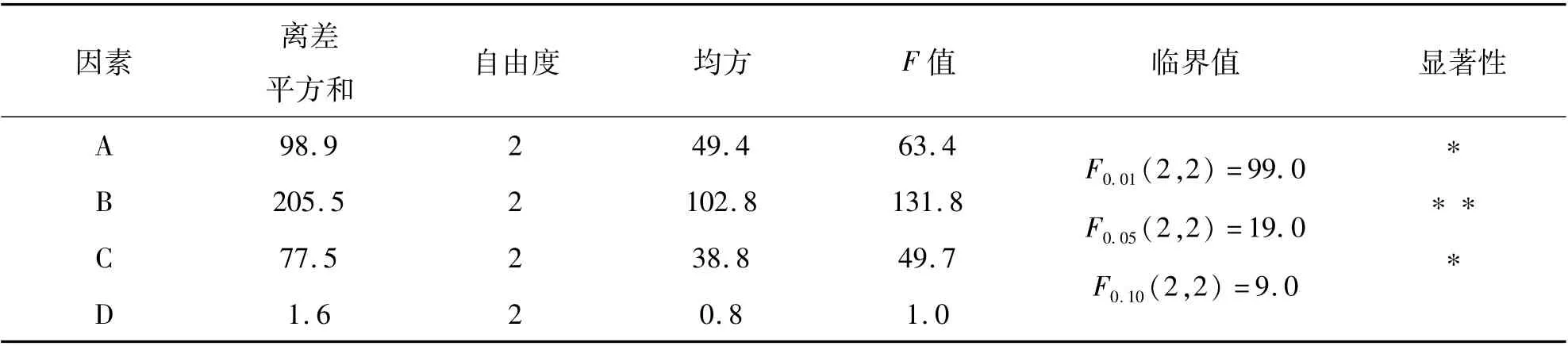
表6 抗弯承载力的方差分析

2.6 承载力-配筋率分析

纵筋配筋率等于纵筋总截面面积与截面有效面积之比[16]，本研究中各试件梁的配筋率随因素B(钢筋直径)和因素C(截面有效高度)的同时变化而改变。 由以上分析可知，因素D(UHPC-CA强度等级)对高强钢筋UHPC-CA梁的抗弯承载力的影响很小，如忽略这一因素，可得到不同钢筋级别(因素A)下抗弯承载力随配筋率的变化，见图3。

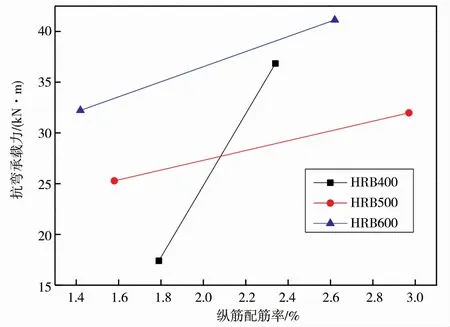
图3 抗弯承载力随纵筋配筋率的变化

从图3 可以看出，对于HRB400 级钢筋系列梁，当配筋率从1.79%增加至2.34%时，高强钢筋UHPC-CA梁的抗弯承载力提升111.7%；对于HRB500 级钢筋系列梁，当配筋率从1.58%增加至2.97%时，梁的抗弯承载力升高26.5%；对于HRB600 级钢筋系列梁，当配筋率由1.42%增加至2.62%时，抗弯承载力增加27.7%。 HRB400 级钢筋系列梁配筋率的增量(0.55%)最低，而承载力提高最多；HRB500 级与HRB600 级钢筋系列梁配筋率的增量接近，分别为1.39%和1.20%，承载力提高幅度接近，且均低于HRB400 级钢筋系列梁。 这一结果表明，纵筋配筋率对普通钢筋(HRB400 级)UHPC-CA梁抗弯承载力的影响较大，而对高强钢筋(HRB500 级、HRB600 级)UHPC-CA梁抗弯承载力的影响相对较小。

3 结论

a)由直观分析可知，正交组合为A3B3C2D1，即钢筋等级是HRB600 级、钢筋直径是18 mm、截面有效高度是162 mm、混凝土强度等级是C130 时，梁的抗弯承载力较高。

b)由极差分析可知，各因素对高强钢筋UHPCCA梁抗弯承载力的影响由大到小依次为钢筋直径＞钢筋等级＞截面有效高度＞混凝土强度等级。

c)由因素指标分析可知，随着钢筋等级、钢筋直径和截面有效高度的增加，抗弯承载力分别提升30.2%、46.8%和26.7%；随着UHPC-CA强度等级的增加，抗弯承载力先略有降低后小幅增长。

d)由矩阵分析可知，在各自因素的3 个水平中，A3(HRB600 级)、B3(18 mm)、C3(181 mm)、D3(C180)对抗弯承载力的影响权重最大。

e)由方差分析可知，钢筋直径为抗弯承载力的重要显著因子，钢筋级别和截面有效高度为一般显著因子，混凝土强度等级为不显著因子。

f)由承载力-配筋率分析可知，随着配筋率的增加，HRB400 级钢筋系列梁的抗弯承载力显著提升，而HRB500 级、HRB600 级钢筋系列梁抗弯承载力的提高幅度相对较小。