基于渗流的改进双强度折减法边坡稳定性分析

周锦涛，肖博文，蒋鹏飞，王雪蓉，黄耀兴

(1.三峡大学水利与环境学院，湖北 宜昌 443000；2.襄阳市南漳县东巩镇人民政府，湖北 襄阳 441528；3.长江三峡通航管理局，湖北 宜昌 443002 )

边坡失稳是工程中常见的问题，严重影响工程安全，而渗流在影响边坡稳定性的因素中占据重要地位，所以在考虑渗流应力耦合作用下如何对边坡的稳定性进行分析是一个十分重要的问题[1]。 近年来，数值模拟计算渗流场应力场耦合状况下边坡的稳定性成为一种主流[2-3]。 卢玉林等[4]在渗流应力双向耦合的基础上探讨了两级边坡渗流耦合破坏的机理。 田杰[5]通过比奥理论研究了渗流应力耦合作用下边坡稳定性。 童富果等[6]通过入渗控制方程的求解计算，实现了渗流场应力场耦合的直接求解。 张仁成等[7]利用水力全耦合分析模型，研究了渗流作用下边坡的位移分布和破坏形式。 这些研究成果在改进渗流耦合模型、强度折减方式方面取得很大进展，但在安全系数的计算方法和安全性上仍有待提高。 本文在考虑渗流应力耦合的情况下采用了改进的双强度折减法，改进了安全系数的计算方式，提高了安全性；通过案例发现，自然工况下，改进的双强度折减法计算结果较传统单强度折减法更安全。 暴雨工况下渗流对边坡安全系数影响比较明显。 因此在考虑渗流影响的条件下采用改进的双强度折减法对边坡进行分析可以得到更符合实际的结果，为实际工程安全提供参考。

1 改进双强度折减法

式中 c、φ——边坡原始黏聚力和内摩擦角，c′、φ′——进行双强度折减后边坡临界状态时的黏聚力和内摩擦角。

边坡失稳过程的实质是边坡的材料强度参数不断的弱化衰减，假设边坡折减比一定时，其临界状态的强度与边坡初始强度无关，边坡临界参数不会随着初始强度参数的改变而发生改变。 因此本文提供一种新的双折减安全系数计算方式。 以内摩擦角和黏聚力作为横纵坐标建立直角坐标系(图1)。

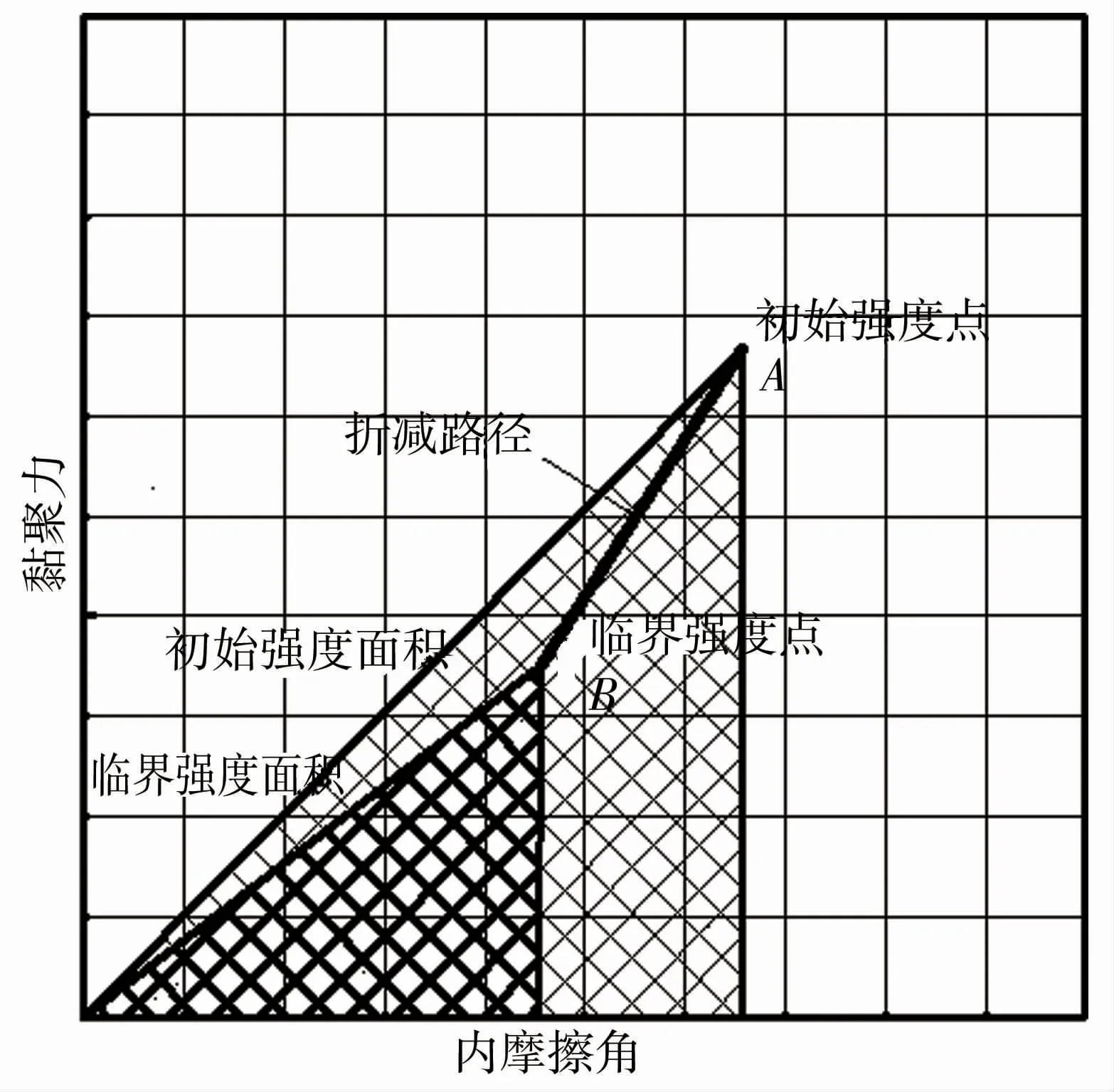
图1 强度坐标系三角形强度面积

A点为边坡的初始强度参数点，其坐标表示初始状态下边坡的黏聚力和内摩擦角，此时与坐标轴围成的三角形面积S1称之为“初始强度面积”；B点为边坡临界强度参数点，所对应的三角形的面积S2称为“临界强度面积”，计算见式(3)、(4)。

S1与S2大小并不代表边坡的强度值的大小，在双强度折减的计算过程中，边坡的强度是通过黏聚力c和内摩擦角φ的折减完成的，而强度面积的定义是直角坐标系的特性，所以可以利用三角形面积去表示双折减过程中强度的变化。

当折减比k=1 时，内摩擦角折减系数SRF1和黏聚力折减系数SRF2在临界状态的取值见式(5):

式(5)可以等价变换为式(6):

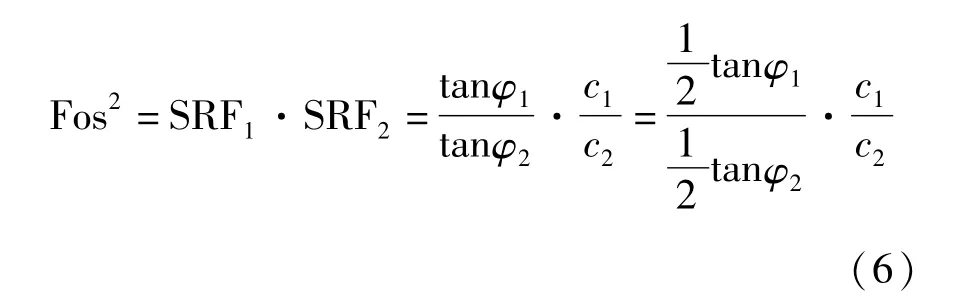
当折减比k≠1 时，在强度参数坐标系中，分子表示初始强度参数点、坐标原点(0，0)、横坐标轴所围成的三角形面积，称为“初始强度面积”，那么同理分母表示临界状态点、坐标原点(0，0)、横坐标轴所围成的三角形面积称为“临界强度面积”，见图1，因此，式(6)又可以表示为式(7):

由此可以得到通过“强度面积”推出的强度双折减的关系为式(8):

式中 SRF1——单独对内摩擦角φ单独进行折减时的折减系数SRFφ；SRF2——单独对黏聚力c进行折减时的折减系数SRFc。

其适用范围为折减比k∈ [0.6，1.4 ]。 此时在直角坐标系中初始强度点与临界强度点之间连线的斜率就是采用不同强度折减比。

2 渗流场和应力场耦合

通过对渗流场和应力场的分析，得到稳定渗流场与应力场耦合分析的连续介质模型[12]。

a)应力场影响下的渗流场数学模型。

c)渗流-应力耦合有限元基本方程。 将渗流场数学模型和应力场数学模型组合起来[13-14]，得到如下双场耦合有限元模型:

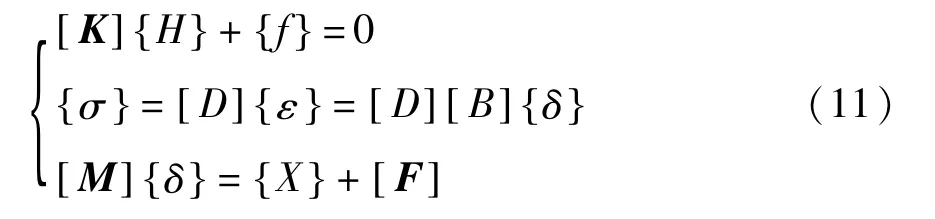
式中 [ ]K——与渗透系数有关的矩阵；[ ]F——与渗透坡降有关的渗透力矩矩阵；[ ]M ——整体刚度矩阵；{ }f——水头分布函数。

若给定边界条件和初始条件，上述双场耦合模型便可通过数值模拟确定耦合效应。 为了更好地把握耦合整体方程的收敛性，本文采用间接耦合的方式对渗流场应力场耦合进行计算。 考虑到上述公式求解比较困难，故用ANSYS 进行渗流计算[15-16]。

3案例分析

3.1 边坡模型的建立

蒋家淌滑坡位于湖北省兴山县大礼溪左岸蒋家趟村，滑坡后缘出现陡坎，高度15 ～18 m，滑体最大水平位移35 m，垂直位移16 m。 选取一个典型坡面建立模型，剖面形式及岩性见图2，各岩土层力学参数见表1。 模型力学边界条件为:底部边界为固定约束，X、Y方向的可变位移为0，左右边界施加水平方向约束，X方向水平位移为0。 渗流边界条件为:底部与左右两侧设置为不透水边界，上部设为透水边界；失稳判据采用特征点位移突变结合塑性区贯通来确定边坡的安全系数。

表1 岩土物理力学参数

图2 典型坡面截面岩性示意

3.2 自然工况下单强度折减法边坡稳定性分析

通过对边坡算例进行分析，得到安全系数与水平最大位移关系和塑性区贯通时的塑性云图，见图3、4。 图中可见，在安全系数为1.37 和1.40 时水平最大位移发生突变。 在安全系数为1.40 时塑性区贯通，故该边坡在采用单强度折减法时，安全系数为1.40。

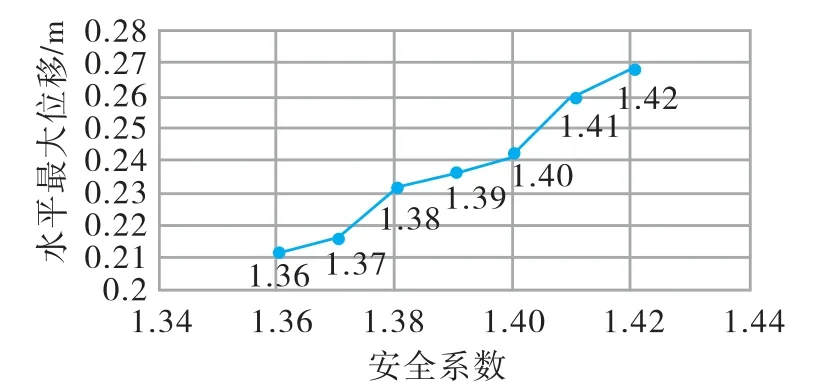
图3 单强度折减安全系数与最大水平位移关系

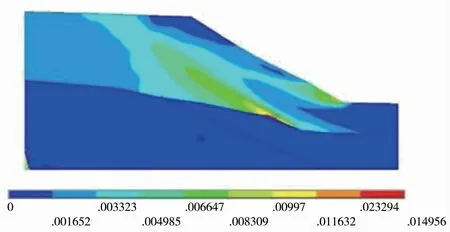
图4 Fos=1.40 时边坡塑性区云图

3.3 自然工况下改进双强度折减边坡稳定性分析

为使误差减小，折减比范围取k∈ [0.8，1.0 )，分别对k等于0.8、0.9 时进行计算。 通过ANSYS和式(1)—(3)得到的具体计算结果，见表2。

表2 自然状态下不同折减比下边坡安全系数及误差

当k=0.8 时，安全系数与水平最大位移关系和塑性云图见图5、6。 由图可知当位移发生突变且塑性区贯通时，安全系数为1.529。 当k=0.9 时，安全系数与最大水平位移关系和塑性云图见图7、8。由图可知当位移发生突变且塑性区贯通时，安全系数为1.328。

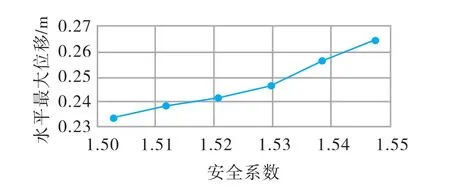
图5 强度折减安全系数与最大水平位移关系(k=0.8)

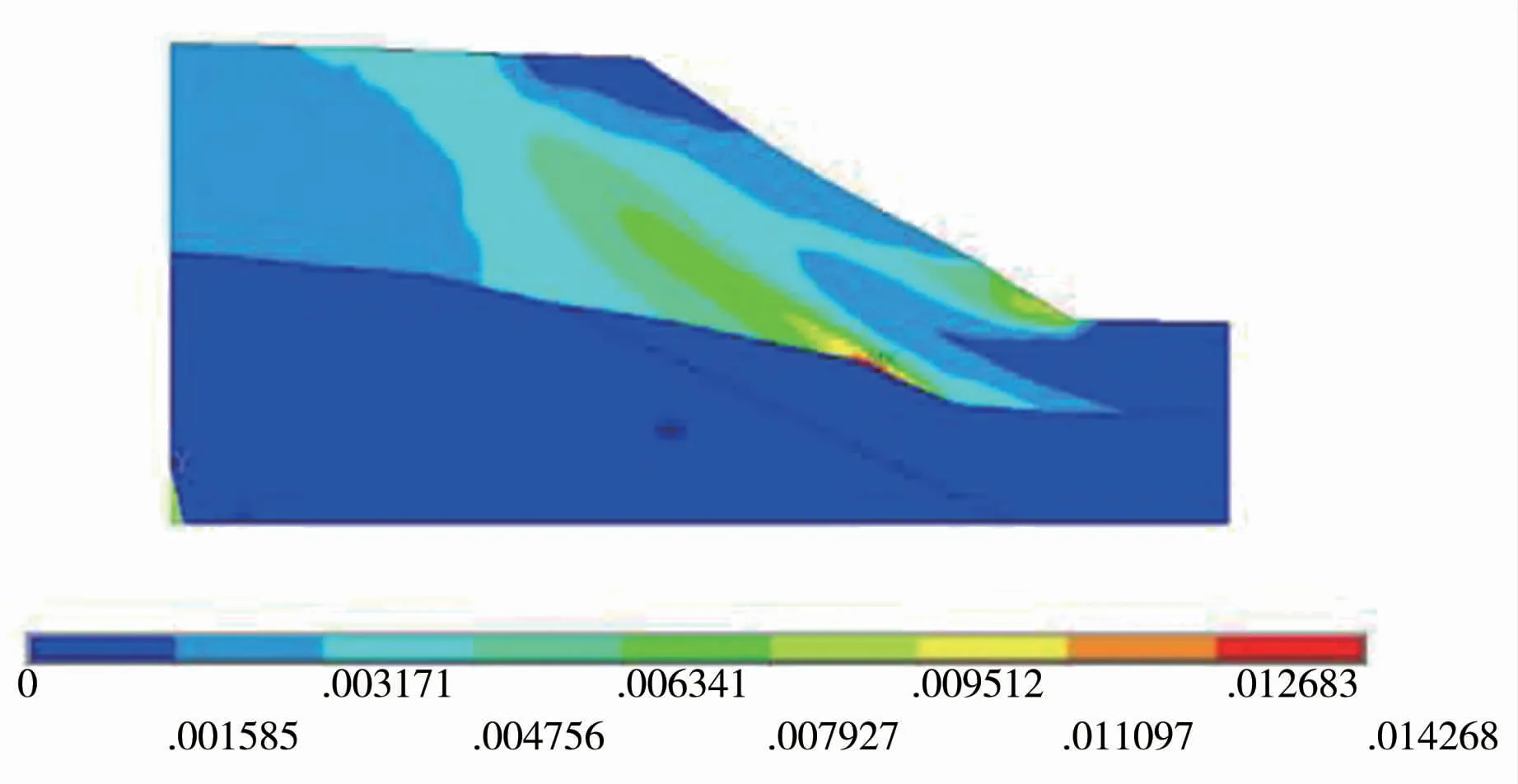
图6 Fos=1.529 时边坡塑性区云图

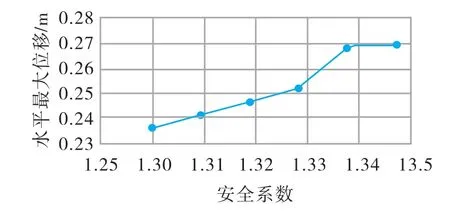
图7 强度折减安全系数与最大水平位移关系(k=0.9)

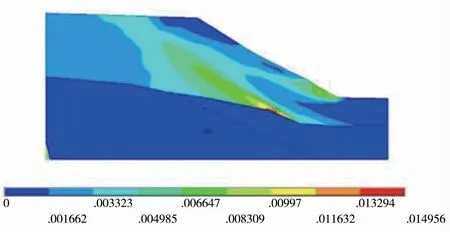
图8 Fos=1.328 时边坡塑性区云图

通过表2 可知，当k取0.8 时，安全系数计算偏差绝对值为9.21%；当k取0.9 时安全系数计算偏差绝对值为5.14%，故折减比取0.9 较为合适，此时安全系数为1.328。

3.4 暴雨工况下渗流应力耦合双强度折减边坡稳定性分析

根据参数条件，通过ANSYS 热分析模块计算出边坡孔隙水压力值，见图9；采用间接耦合的方法对渗流场与应力场进行耦合，用改进强度双强度折减法对边坡进行计算。

图9 孔隙水压力等值线

折减比取为0.9 时，安全系数与最大位移关系和塑性云图，见图10、11，图中可见在安全系数为0.97 时位移发生突变，同时塑性区贯通，故考虑渗流时边坡安全系数为0.97。

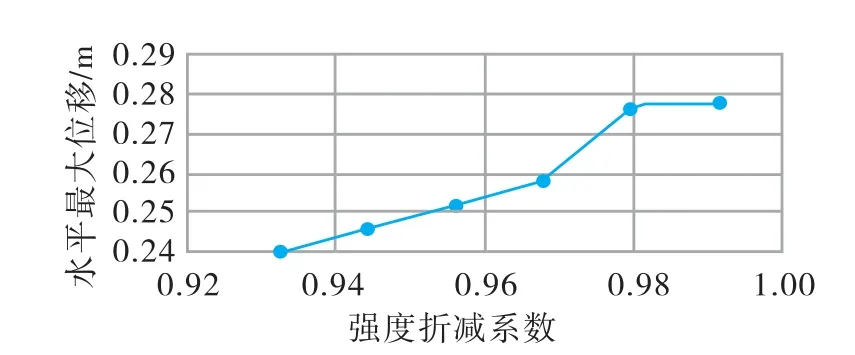
图10 强度折减安全系数与最大水平位移关系(k=0.9)

图11 Fos=0.97 时边坡塑性区云图

3.5 结果对比

对比3 种计算结果，见表3。 自然工况下，改进双强度折减法计算出的安全系数为1.328，传统单强度折减法计算出的安全系数为1.400，误差绝对值为5.42%，说明该方法计算安全系数是可行的；暴雨工况下，即考虑渗流的情况下，改进双强度折减法计算出的安全系数为0.97，渗流应力耦合情况下安全系数较自然工况降低了27%，可知渗流对边坡的稳定性有显著影响。

表3 不同折减方式下边坡安全系数

4 结论

a)采用改进双强度折减法对边坡进行分析，改善了传统单强度折减法中因为黏聚力c与内摩擦角φ按相同的折减速度进行折减从而掩盖c与φ在保持坡体稳定性中发挥着不同作用的问题。

b)对边坡进行了2 种工况，3 种计算方式的分析，发现折减比k的范围在 [0.8，1.0 )较为合适，结果表明取0.9 最为合理，极大程度地减少了试算过程中的工作量，提高了安全系数的计算效率。

c)相同工况下，采用改进双强度折减法对边坡进行分析时所得结果较传统单强度折减法降低了5.42%，说明该方法计算安全系数是可行的，并且更安全。

d)渗流对边坡的稳定性影响比较明显，达到了27.00%，在边坡失稳过程中，不同的水荷载分布对应着相应的渗流场分布，渗流场改变了岩土介质中水荷载分布进而改变了应力场，因此在进行边坡的稳定性分析中不可忽略渗流应力的影响。 即边坡在自然情况下处于安全状态，当考虑渗流影响时仍可能发生失稳，所以本文采用的考虑渗流的改进双强度折减法可以得到更符合实际的结果，为实际工程提供参考。