东江流域气象干旱向水文干旱传递阈值研究

莫晓梅，涂新军，2，3*，王 天，谢育廷，赵国羊

(1.中山大学土木工程学院水资源与环境研究中心，广东 广州 510275；2.广东省华南地区水安全调控工程技术研究中心，广东 广州 510275；3.南方海洋科学与工程广东省实验室，广东 珠海 519000)

干旱是指由于水分的收支或供求不平衡形成的水分短缺现象[1]。 干旱在世界范围内仍是发生频率最高、影响范围最广、致灾损失最大的自然灾害之一[2-3]。 全球因干旱导致的经济损失高达60 ～80亿美金，远超其他自然灾害[4-5]。 无论是基于水循环组分角度或研究对象要素角度，均可以将干旱分为气象干旱、水文干旱、农业干旱和社会经济干旱4类[6]。 其中，气象干旱主要是基于降水量不足而导致的干旱，水文干旱则是由于径流量不足而导致的干旱[7]。 气象干旱作为所有干旱发生的源头，也是最普遍和最基本的干旱类型，水文干旱则更能反应旱情，且影响因素较气象干旱复杂，影响程度更深[8]。 二者反应了干旱事件的不同阶段，通常认为水文干旱是气象干旱的延续，并直接影响农业干旱和社会经济干旱。 此外，从气象干旱到水文干旱的过程会受到土地利用因素、产汇流过程以及土壤性质等因素的影响[9-11]。

总体而言，研究基于不同水文气象要素形成的气象干旱到水文干旱的传递，可以在机理上揭示干旱传播途径和干旱形成过程。 因此，在干旱传递的过程中，量化传递规律是十分必要的。 有研究从干旱指数相关性的角度，分析水文干旱滞后于气象干旱的时间，以表征干旱传递特征[12]。 除通过干旱指数判断外，直接通过降雨、地下水和径流等影响要素对干旱传递进行判断也是一种适合的判断方法[13]。尽管上述2 种方法在一定程度上解决了定量化阈值的问题，但都将2 种类型的干旱进行了剥离，这将会导致2 种干旱无法在时间上统一。 同时，2 种不同干旱指数之间的分布状况不一致，也会造成结果的失真。

因此，本文基于之前学者研究存在的问题，在东江流域提出一种更适合定量化判断干旱传递阈值的方法。 首先，计算东江流域月尺度的标准化降水指数(Standardized Precipitation Index，SPI)和标准化径流指数(Standardized Runoff Index，SRI)指数。 其次，通过游程理论提取干旱事件及其特征，如历时和烈度，并对发生时间部分或全部重叠的气象干旱事件和水文干旱事件进行匹配。 最后，利用二变量Copula函数，构建气象干旱和水文干旱的特征属性的联合分布模型，通过条件概率分析，识别气象干旱向水文干旱传递阈值。

1 研究区域概况及数据来源

东江为珠江流域三大水系之一，流域控制站博罗站以上的集水面积为25 325 km2。 东江流域属于亚热带季风气候，流域多年平均降水量为1 500 ～2 400 mm，降雨时间上分配不均，4—9 月为雨季，降水量达全年降水量的80%，10 月到翌年3 月为旱季，降水量仅为全年降水量的20%。 东江担负着为珠三角地区4 000 多万人口提供生产、生活、生态用水的重任，因此研究东江流域干旱情况对社会和经济发展有着重要意义。 研究数据为中国国家气象局气象信息中心提供的东江流域内34 个主要气象站1956 年4 月至2009 年3 月的月降水数据和博罗水文站1956 年4 月至2009 年3 月的实测月径流数据，并根据流域三大水库(新丰江水库、枫树坝水库和白盆珠水库)的月径流调蓄量，还原得到天然径流数据。 站点分布见图1。

图1 东江流域及站点分布

2 研究方法

2.1 干旱指数计算

由于SPI指数可以表征一定时期内降雨发生概率，该指标不但适用于多时间尺度的气象干旱描述，而且能够很好地反映干旱的强度和持续时间，因此被广泛使用[14]。 SRI指数与SPI指数类似，计算方法简单，同样适用于多时间尺度分析，对资料缺乏、地形复杂的区域也有很好的适应性，目前在水文干旱识别研究中应用广泛[15]。 因此，本文分别采用SPI指数和SRI指数来表征气象干旱和水文干旱，2种指数的计算方法如下。

SPI指数计算采用常用3 参数Log-logistic概率分布模型，其累积概率函数见式(1):

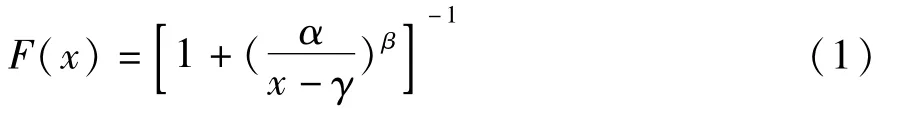
式中 (x|Xi=1，…，n)——降水系列；n——样本系列的长度；α、β、γ——基于样本系列通过线性矩法拟合而得的参数。

对累积概率进行标准化转换，有:

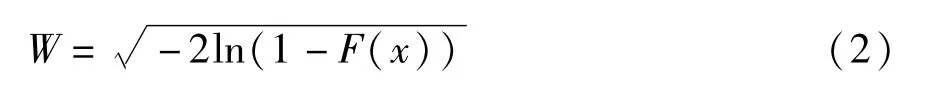
因此，干旱指数SPI为:

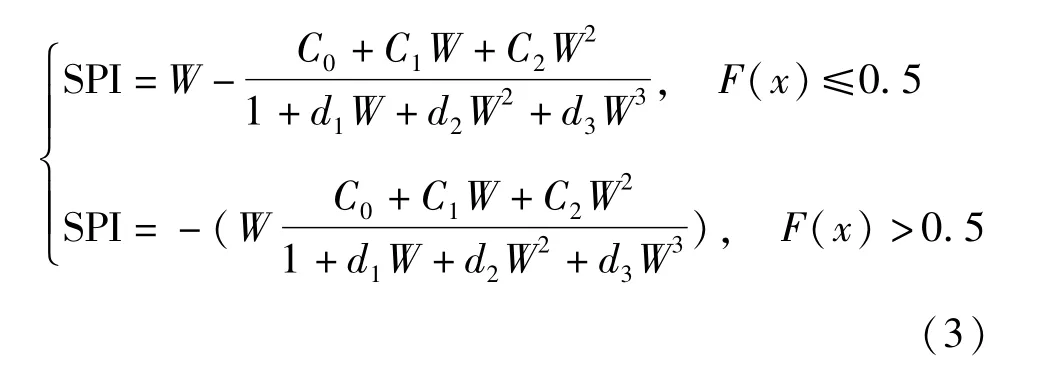
式中，C0=2.515 517；C1=0.802 853；C2=0.010 328；d1=1.432 788；d2=0.189 269；d3=0.001 308[16]。

以SPI指数的计算理论为基础，以径流值代替原SPI计算过程的降水值，即可得到标准化径流指数SRI[17]。

2.2 干旱事件识别

游程理论是分析时间序列的一种方法，经过长时间的发展和应用，目前被广泛应用于干旱事件的识别中[18-19]。 游程理论可以有效地从连续的干旱事件中提取干旱事件的历时D(Duration)和烈度S(Severity)。 历时是指干旱事件持续时间，烈度是干旱事件中指标值与截取水平差值之和，研究中通常取其相反数。

本文不仅通过游程理论对干旱事件进行识别，同时为了避免次要干旱事件导致干旱传递模型被破坏，同时采用了干旱事件的融合和剔除方法[20]。 具体步骤如下[21]:①当指数值小于R1，初步识别为干旱事件；②对于干旱历时仅为1 个月的干旱事件，若指数值大于R2，则该干旱事件应被剔除；③对于间隔时间为1 个月的2 个干旱事件，若间隔月份的干旱指数值小于R0，则将这2 个干旱事件合并为1 个干旱事件。 图2 中干旱事件a、b分别识别为2 次独立的干旱事件，但其间隔月份为1 个月，且该月干旱指数小于R0，因此将a、b及其间隔融合为1 次干旱事件进行考虑，合并后，干旱历时(烈度)为2 个干旱事件历时(烈度)之和。 本文R0=0，R1=0.3，R2=0.5[22-24]，示意见图2。

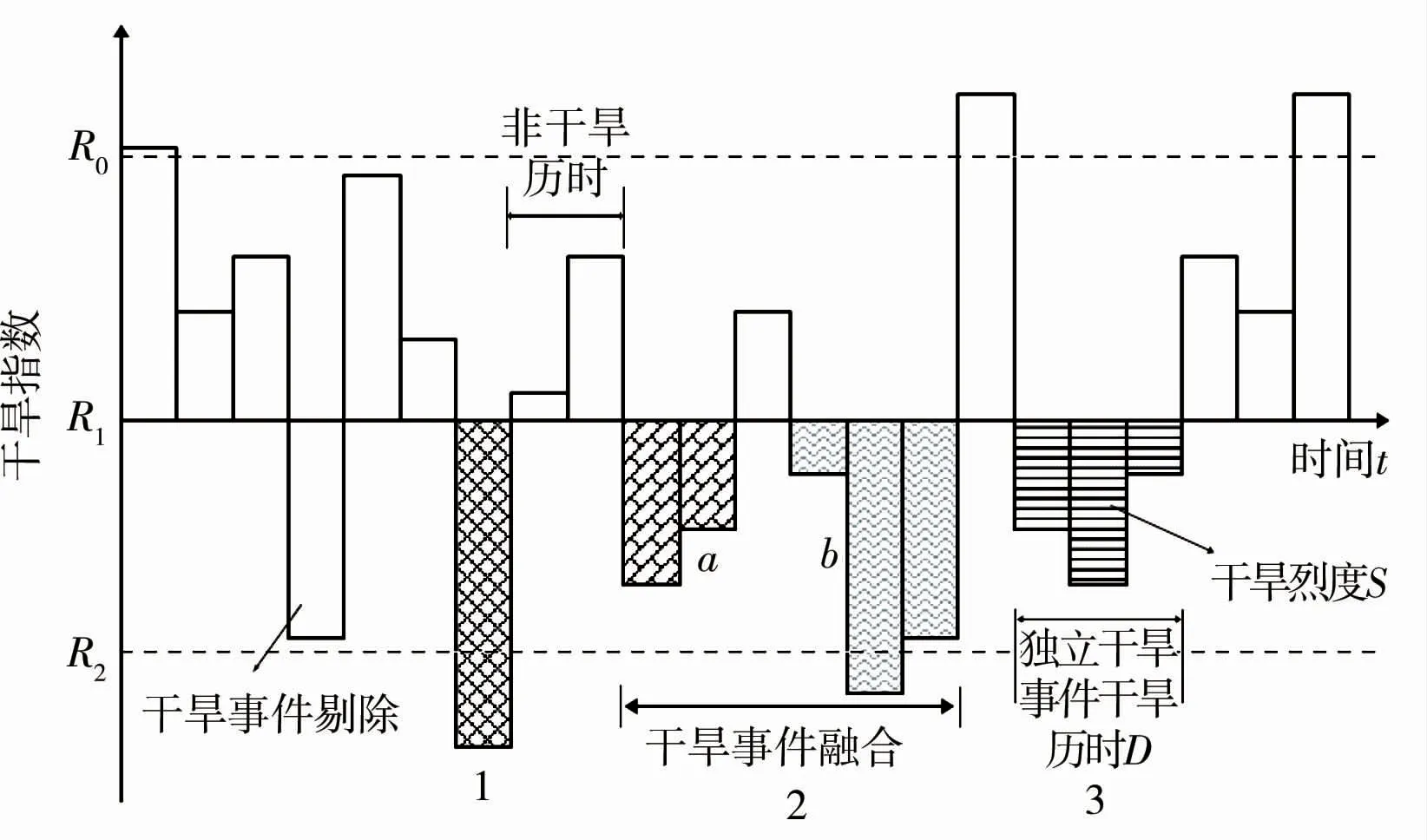
图2 游程理论示意

2.3 干旱传递模型的构建

Copula函数是由Sklar[25]在1959 年提出，已经广泛地应用在气象水文领域。 该理论的原理相对简单，认为任意一个多维度联合分布函数可以由一个Copula函数和多个边缘分布函数构成，并且允许多个边缘分布函数的分布概率存在差异，可以用于描述任意变量间的联合分布情况。 因此，拟采用二变量Copula函数构建气象-水文干旱传递模型。

二变量Copula模拟主要包括边缘分布函数拟合及优选、Copula函数拟合及优选、联合概率或条件概率分析等4 个过程。 以历时为例，气象-水文干旱传递模型的构建方法为:①选择伽玛分布、对数正态分布、广义正态分布、皮尔逊三型等单变量分布模型，对气象干旱历时和水文干旱历时进行边缘分布拟合，确定各自最优边缘分布函数；②分析气象干旱历时和水文干旱历时的相关性，若其相关性较强，符合构建Copula函数的条件； ③选择Gaussian、Gumbel、Frank 和Clayton 等常用二变量Copula函数，模拟气象干旱历时和水文干旱历时联合分布，选择最优Copula函数；④计算中旱、重旱、极旱3 个等级的水文干旱发生的气象干旱条件概率，基于条件概率确定该等级干旱历时传递阈值。

2.3.1 拟合边缘分布

拟合边缘分布是构建Copula函数的首要任务，目前常见的4 种单变量函数是伽玛分布、对数正态分布、广义正态分布、皮尔逊三型分布。 本文设气象干旱历时和烈度的边缘分布函数分别为FM(d)、FM(s)，水文干旱历时和烈度的边缘分布函数分别为FH(d)、FH(s)，采用上述边缘分布函数对气象干旱、水文干旱的历时、烈度进行拟合，用Anderson-Darling test(A-D)检验法[26]进行拟合优度的检验，认为处于95%置信区间的统计量符合检验要求，即通过检验。 同时，采用Kendall秩相关系数、Pearson相关系数和Spearman 秩相关系数等方法表征干旱历时和干旱烈度之间的相关性。

2.3.2 Copula拟合

Copula函数是连接单变量边缘分布，形成在[0，1]区间上服从均匀分布的多元函数。 由Copula函数的定义可知，气象干旱历时FM(d)和水文干旱历时FH(d)的联合分布函数为:

同理可以计算气象干旱烈度FM(s)和水文干旱烈度FH(s)的联合Copula函数。 文中选取常用的理论二变量Copula函数Gaussian-copula和Claytoncopula、Frank-copula、Gumbel-copula[27]。 计算理论Copula值与经验Copula值之间的均方根误差RMSE[28]评价Copula函数的拟合优度。

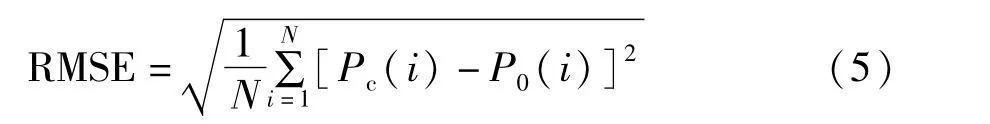
式中 N——样本容量；Pc(i)——实测概率值；P0(i)——Copula函数计算得到的概率值。

2.3.3 条件概率

假设X、Y为2 个随机变量，则X≥u 条件下Y≥v的条件概率可表示为:

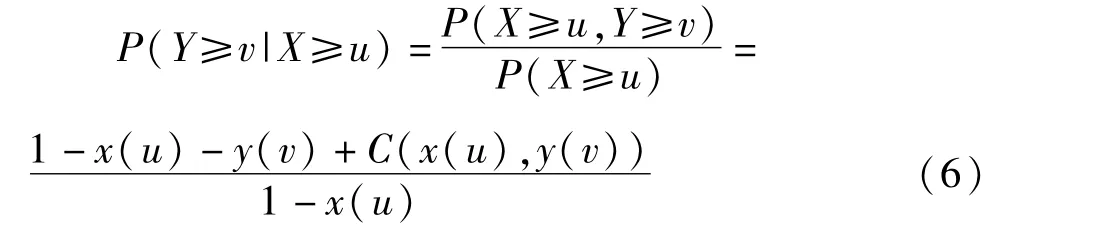
式中 x、y——随机变量X、Y的边缘分布；x(u)、y(v)——X≤u 和Y≤v时的累积概率；C(x(u)，y(v))——X≤u 和Y≤v时的联合概率。

本文X为气象干旱特征，Y为不同等级的水文干旱特征。 干旱通常分为轻旱、中旱、重旱和极旱4个等级[29]，表1 所示，轻旱、中旱、重旱和极旱等级干旱事件的累积概率区间为(0，0.5)、[0.5，0.75)、[0.75，0.9)和[0.9，1)[30-31]。 构造了气象干旱特征和水文干旱特征的联合分布模型后，根据式(6)计算气象干旱特征大于某一个值时水文干旱等级超过中旱、重旱、极旱的条件概率。 随着气象干旱条件的增加，条件概率逐渐接近1。 本文选取干旱传播阈值的置信水平为0.95[22]，即当条件概率等于0.95 时，对应的气象干旱特征值被视为该等级水文干旱的干旱特征传递阈值，干旱等级划分见表1。

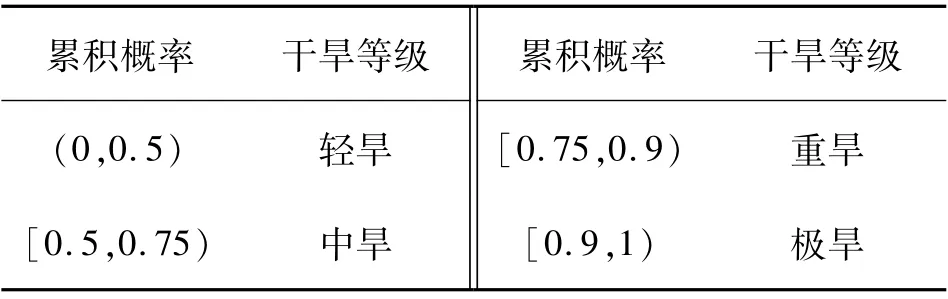
表1 干旱等级划分

3 结果分析

3.1 干旱指数特征

东江流域月尺度的SPI和SRI见图3，大部分年份SPI值比SRI小。 SPI的最小值为-1.45，出现在1979 年10 月，最大值为2.55，出现在1966 年6 月。SRI的最小值为-1.60，出现在1963 年5 月，最大值为2.52，出现在1959 年6 月。 SPI的最大值和最小值均比SRI大。

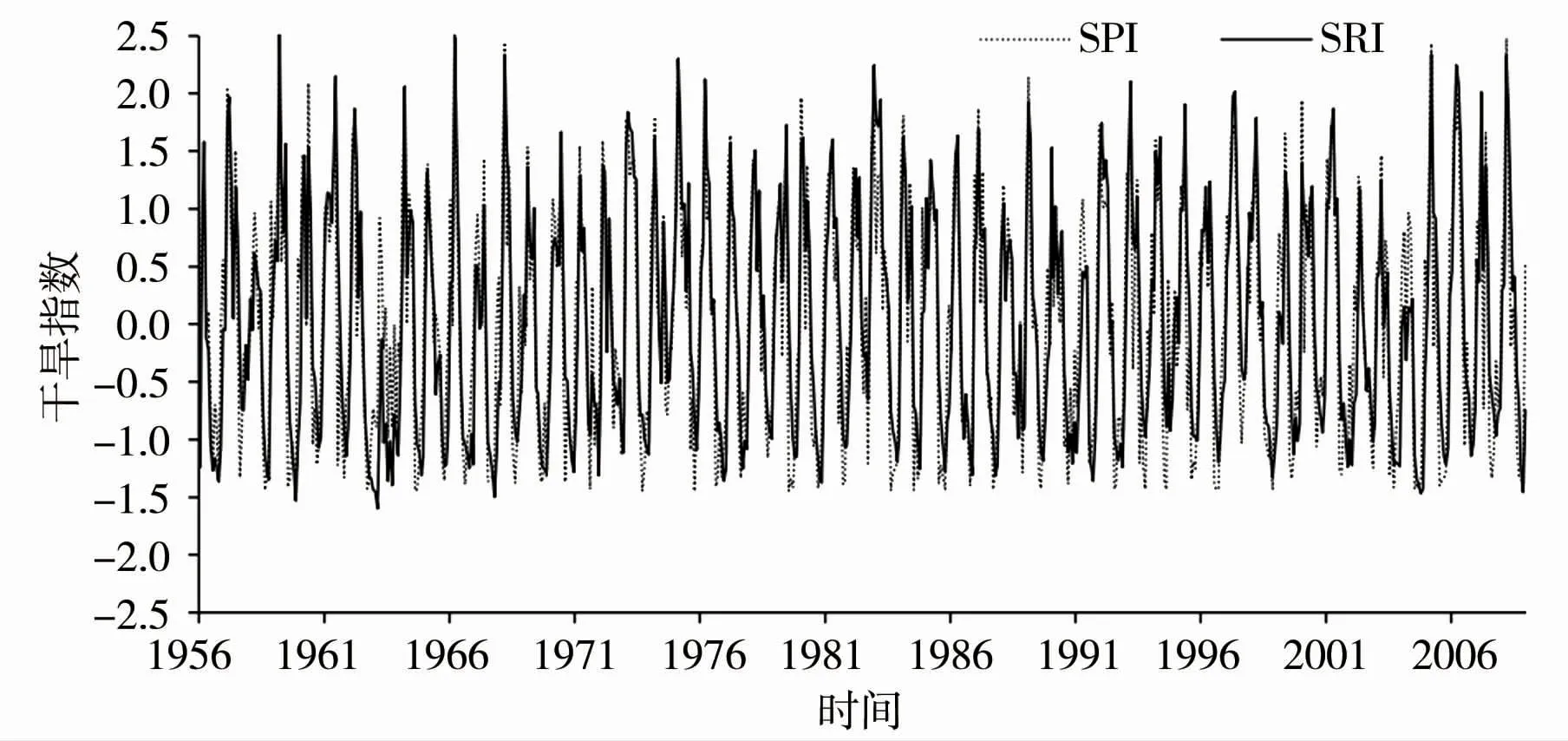
图3 东江流域月尺度的SPI和SRI

气象干旱和水文干旱均表现为春旱(1—3 月)和冬旱(10—12 月)。 但气象干旱一般出现于10 月份，于次年2 月份结束，平均持续时间为4 个月。 历时最长的气象干旱出现在1962 年11 月至1963 年5月、1963 年10 月至1964 年4 月、2001 年10 月至2002 年4 月，历时均为7 个月。 水文干旱一般出现于10 月份，于翌年3 月份结束，平均持续时间为5个月。 历时最长的水文干旱出现在1962 年11 月至1964 年4 月，历时18 个月。 同时，对于气象干旱，轻旱等级所占比例由55.5%下降至37.2%，中旱等级所占比例由44.6%上升至62.8%，进入21 世纪后轻旱所占比例上升至47.5%，中旱等级所占比例减少至52.5%，与气象干旱相比水文干旱变化规律不明显。

3.2 干旱事件及其特征

计算干旱指数后，根据游程理论提取干旱事件。东江流域发生气象干旱事件62 次，发生水文干旱事件54 次。 对时间上存在部分或全部重叠的干旱事件进行匹配。 例如1956 年9 月至1957 年1 月发生历时为5 个月的气象干旱，1956 年9 月至1957 年2月发生历时为6 个月的水文干旱，二者在发生时间上部分重叠，可匹配。 匹配后有干旱事件45 次。 匹配后干旱特征箱型见图4，统计参数见表2。 气象干旱历时均值为4.8 个月，最小值为1 个月，最大值为7 个月；烈度均值为3.24，最小值为0.91，最大值为4.93；水文干旱历时均值为5.42 个月，最小值为1个月，最大值为8 个月；烈度均值为3.11，最小值为0.35，最大值为5.42。 水文干旱相对气象干旱平均历时长，烈度小。

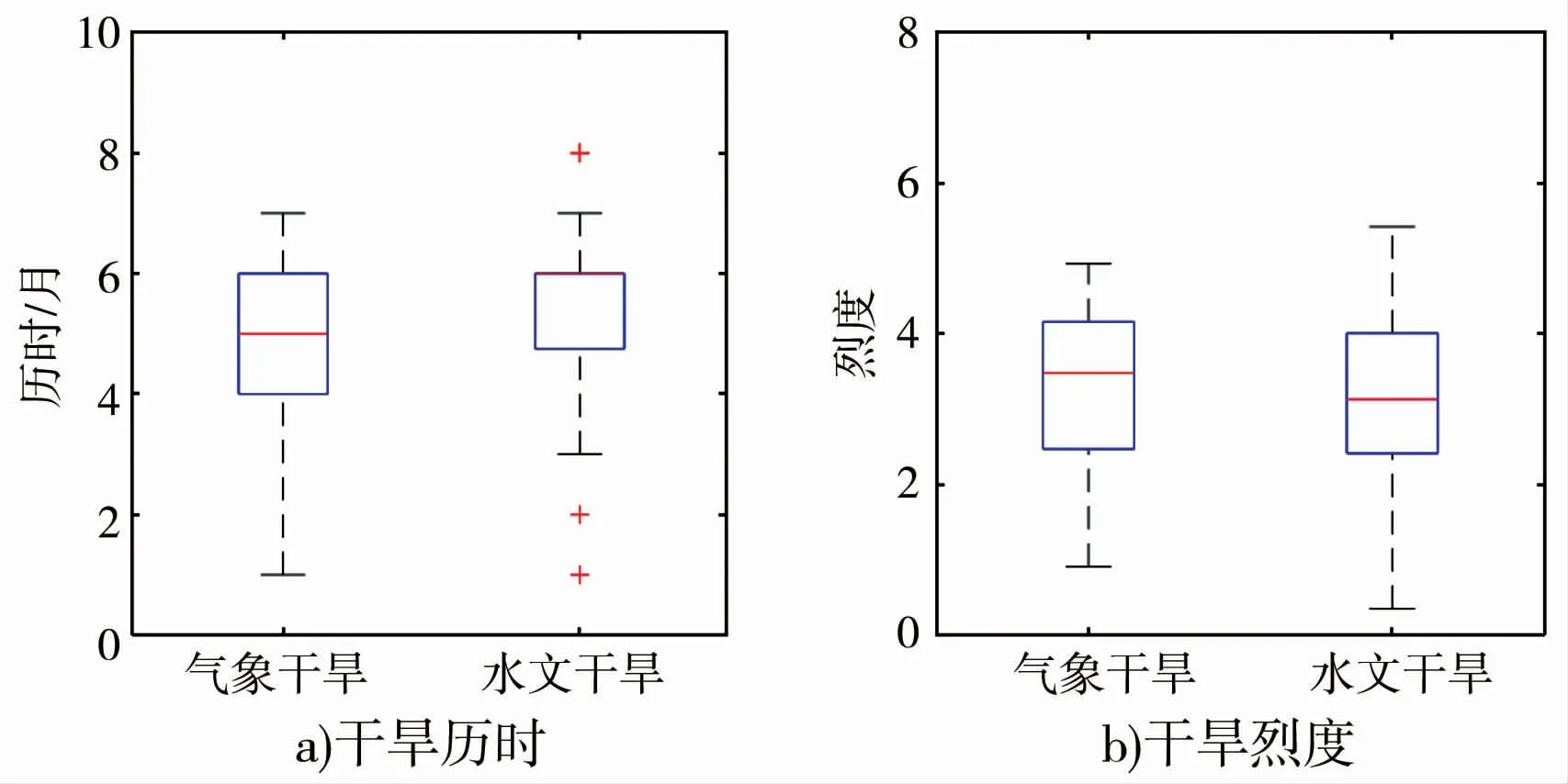
图4 干旱特征箱型

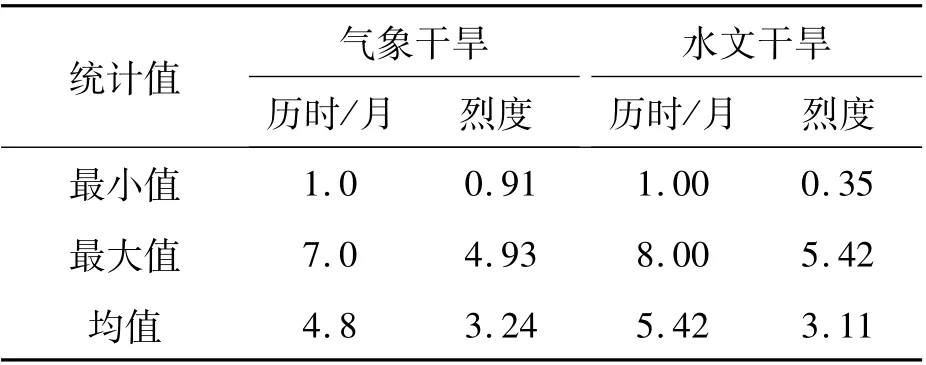
表2 干旱特征的统计参数

3.3 气象-水文干旱联合分布拟合

识别干旱事件后，采用伽玛分布、对数正态分布、广义正态分布、皮尔逊三型分布对匹配后的气象干旱和水文干旱的历时和烈度分别进行拟合，在通过显著性检验的前提下，结合历时和烈度的累积概率曲线图，根据AIC最小原则，选择最优拟合函数。各个边缘分布函数对历时和烈度的拟合效果见图5，拟合参数见表3。 气象干旱历时和烈度的最优拟合函数均为伽玛分布，水文干旱历时的最优边缘分布函数为伽玛分布，水文干旱烈度的边缘分布函数为广义正态分布。 采用Kendall秩相关系数、Pearson 相关系数和Spearman 秩相关系数计算气象干旱历时(烈度)和水文干旱历时(烈度)之间的相关性，结果见表4，变量呈明显的正相关关系，其中，气象干旱烈度与水文干旱烈度之间的相关性较高。

图5 边缘分布函数拟合效果

表3 边缘分布函数统计检验P值

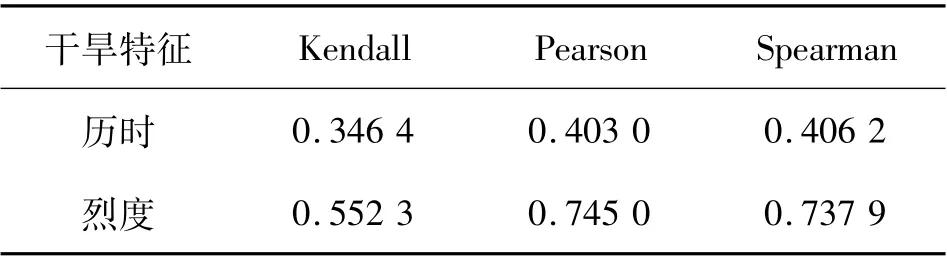
表4 气象干旱-水文干旱特征相关系数

建立气象干旱历时(或烈度)和水文干旱历时(或烈度)的二变量Copula函数，并计算理论Copula值和经验Copula值的RMSE验证Copula函数的拟合效果。 表5 为评价指标RMSE的值，其中RMSE越小，说明Copula函数拟合效果越好。 对于烈度，Gaussian-copula的RMSE值最小，为0.047 2；对于历时，Gumbel-copula的RMSE值最小，为0.094 6。 说明Copula函数拟合效果满足预期要求，且满足程度较高。 由于不同Copula函数的结构不同，会导致Copula函数的选择影响分析结果。 因此，本文统一采用Gumbel-copula对干旱特征进行拟合。

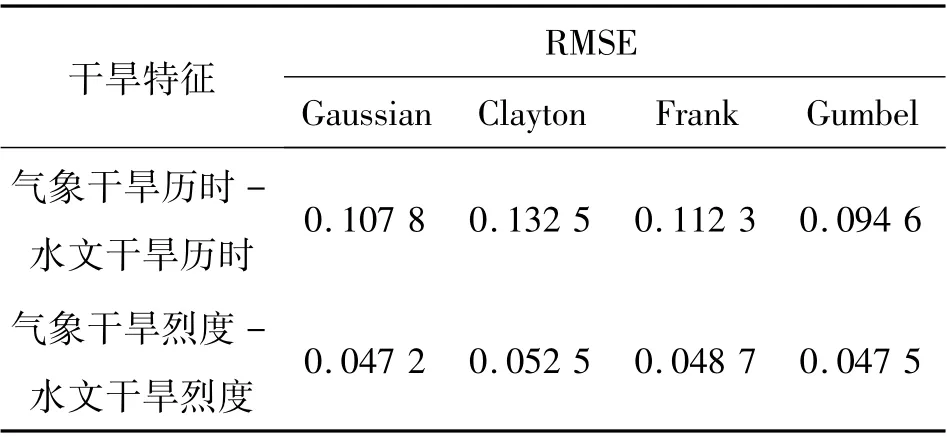
表5 Copula 函数拟合效果评价指标

3.4 气象干旱向水文干旱传递分析

本文构建Copula函数后，计算了给定气象干旱历时(烈度)超过某一值条件下水文干旱等级大于中旱(累积概率大于0.5)、重旱(累积概率大于0.75)和极旱(累积概率大于0.9)的概率分布。 不同气象干旱特征下，中旱、重旱和极旱等级水文干旱发生的条件概率见图6。 结果表明，相同气象干旱特征下，水文干旱的条件概率随着干旱等级的增加而减小。 条件概率曲线呈“S”形，在条件概率接近0.95 时，随着气象干旱特征的增加，条件概率曲线趋于平缓。 截取条件概率为0.95 时的干旱特征值作为干旱传递的阈值。 东江流域中旱、重旱和极旱等级的水文干旱历时和烈度的阈值为6.9、8.3、9.4个月和4.6、5.7、6.6。 随着干旱等级的增加，干旱的阈值也相应增加。

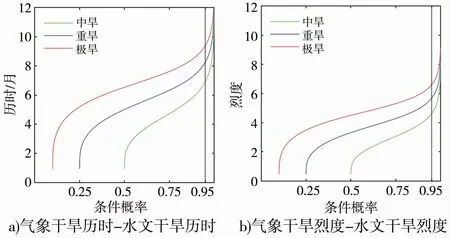
图6 气象干旱向水文干旱传递的条件概率

4 结论

计算东江流域的SPI指数和SRI指数，根据游程理论提取干旱历时和烈度，对干旱特征进行边缘分布拟合，建立气象干旱历时(烈度)和水文干旱历时(烈度)的二元Copula模型，计算不同气象干旱条件下中旱、中旱、极旱水文干旱发生的条件概率，截取条件概率为0.95 时的气象干旱特征值作为干旱传递阈值。 主要结论如下。

a)SPI和SRI分别体现了气象干旱和水文干旱严重程度，根据游程理论识别了气象干旱62 次，水文干旱54 次，历时最长的气象干旱为7 个月，出现在1962 年11 月至1963 年5 月、1963 年10 月至1964 年4 月、2001 年10 月至2002 年4 月，历时最长的水文干旱为18 个月，出现在1962 年11 月至1964年4 月，匹配后干旱事件45 次。

b)通过A-D检验方法对边缘分布拟合结果进行检验，气象干旱历时和烈度的最优拟合函数均为伽马分布，水文干旱历时和烈度的最优拟合函数分别为伽玛分布、广义正态分布。 通过RMSE结果对比4 种Copula函数的拟合效果，Gumbel-copula函数的拟合效果最优，则选择Gumbel-copula函数构建干旱传递模型。

c)气象-水文干旱特征联合分布条件概率取0.95 时，东江流域中旱、重旱和极旱的干旱历时传递阈值分别为6.9、8.3、9.4 个月，干旱烈度传递阈值分别为4.6、5.7、6.6。