基于噪声子空间特性的波束形成器设计

黄翔东, 赵一冉, 苗 笛

(1.天津大学电气自动化与信息工程学院, 天津 300072; 2.天津职业技术师范大学电子工程学院, 天津 300222)

0 引 言

鲁棒自适应波束形成(robust adaptive beamforming, RAB)一直是阵列信号处理领域的研究热题。通过调整权重,控制阵列中各个阵元输出,使其在期望信号方向形成增益;在干扰信号方向设置零陷,实现放大期望信号同时抑制干扰信号的目的。因而在雷达、声呐、移动通信、卫星导航等领域被广泛应用[1-4]。

传统标准Capon波束形成器[5](standard Capon beamformer, SCB)因其具有较高分辨率和较强抗干扰能力,而被作为基本模型广泛采用。然而当快拍数较少、期望信号失配、观测数据包含期望信号时,传统波束形成器的性能会严重下降。因此,提高期望信号的适配度和干扰加噪声协方差矩阵(interference plus noise covariance matrix, INCM)的估计精度是改善波束性能的根本途径。近年来,自适应波束形成器主要围绕两个方面进行改进:对角加载方法和基于子空间分解的方法。

对角加载方法是通过在样本协方差矩阵上增加一个尺度单位矩阵,或对方向向量施加二次约束而实现的[6],其优点在于可有效地降低波束形成器对快拍数的依赖度;但其缺陷在于:难以选择适用于不同环境下最优的对角加载因子,且当输入信噪比较高时,其性能下降严重[7-8]。

而基于子空间分解的思路是:对样本协方差矩阵做有效的处理,将观测空间分解为期望信号子空间、干扰子空间和噪声子空间,从中估计出INCM,再进一步结合标准SCB而完成波束形成器设计[9]。具体地,一方面,需要提升INCM的估计精度,另一方面,需要降低构造INCM的复杂度[10-11]。

文献[12]通过在期望信号入射角度以外的所有区间对Capon空间谱进行积分,首次解决了不可观测的INCM的估计问题,然而这种大范围的数值积分也带来了高计算复杂度;文献[13]在文献[12]基础上做出改进,利用一阶泰勒级数逼近期望信号方向向量,提升了Capon空间谱积分区间的精度,从而优化了波束性能,但仍然没有解决大范围积分带来的高计算复杂度的问题;文献[14]提出用空间谱采样的方法重构INCM,大大减少了计算复杂度,然而算法对阵元数量有较高的需求;文献[15]通过剔除Capon空间谱积分的残留噪声影响,不仅降低了计算复杂度,而且进一步提升了波束性能;然而文献[14-15]设计均建立在信号空间与干扰空间正交的基础上,而实际应用中这一假设往往不严格成立;文献[16]则利用了噪声空间和信号空间的正交性,通过构造阻塞矩阵实现了INCM的高精度估计和高性能波束形成器的设计,然而该设计要求期望信号功率远高于噪声功率,这限制了其实际应用。

为克服以上不足,提出基于噪声子空间特性的波束形成器的设计,其作用机理体现在: ① 利用噪声子空间的宽带分布特性,对期望信号和干扰以外的区间进行粗采样,计算出残留噪声,并将之作为补偿量, 获得信号协方差矩阵的估计;② 利用噪声子空间与信号子空间的正交性,对信号协方差矩阵进行分解,从中构造出信号正交补投影算子;③ 利用噪声子空间与干扰子空间的正交性,用信号正交补投影算子对观测信号进行处理,获得干扰功率的高精度估计。充分利用噪声空间以上特性,可确保高精度设计出波束形成器,由于以上数值积分均在窄空间上实现的,因而本设计的计算复杂度较低。仿真结果验证了所提算法的有效性。

1 系统模型

考虑由M个阵元组成的均匀线性阵列接收远场信号,假设有一个期望信号和J个干扰信号,期望信号入射角度为θ0,干扰信号波达角(direction of arrival, DOA)为θi,i=1,2,…,J。则在k时刻的阵列接收信号可以建模为

x(k)=s(k)+i(k)+n(k)

(1)

(2)

式中：se(k)为期望信号复包络；a0为期望信号方向向量;ai为干扰信号方向向量；si(k)是为干扰信号复包络。假设期望信号、干扰和噪声各自统计独立。

令λ表示信号波长，d为阵元间距,则对于任一入射角度θ的方向向量可表示为

(3)

式中：T表示转置,不难证明,该方向向量的l2-范数为

(4)

不妨将接收机的M个阵元上的权重矢量表示为w=[w1,w2,…,wM]T,则在k时刻可获得波束输出:

y(k)=wHx(k)

(5)

式中：H表示共轭转置；最优权重矢量w可以在输出信干噪比(signal to interference plus noise ratio, SINR)取到最大值时得到

(6)

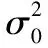
(7)

文献[5]指出,式(6)取最大值的问题等价于下面的优化问题:

s.t.wHa0=1

(8)

式(8)即为Capon波束形成器[5],其解为

(9)

实际应用中,由于Ri+n无法直接观测得到,通常用下式样本协方差矩阵代替：

(10)

式中：K为快拍数。此时的最佳权重矢量为

(11)

式(11)为由样本协方差矩阵近似推出的波束形成器,对期望信号方向向量失配较为敏感,尤其是当高信噪比(signal to noise ratio, SNR)时,性能下降严重。

因而,高效、高精度估计出式(9)中的INCM(即Ri+n)是RAB设计的关键所在。

2 算法原理

2.1 基于残留噪声补偿的信号方向向量估计

式(10)对应的Capon空间功率谱为

(12)

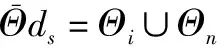
(13)

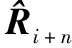
证明设x(k)的期望信号的入射角度和功率分别为θs、σ2,不妨聚焦于期望信号的角度区域Θs,则该区域的协方差矩阵为

(14)

将式(14)代入式(12),且令θ=θs,则可推导出在期望信号入射方向处的Capon空间谱功率值为

(15)

(16)

考虑到在Θs、Θi、Θn中,噪声区域Θn的范围最大,故为降低大范围内的数值积分造成的误差累积,且考虑到噪声特性在Θn内的一致性,仅在Θn内随机选取少数采样点进行数值积分。相应地,残留噪声可估算为

(17)

式中：θn是Θn中随机采样点；N为采样点个数。由于式(17)用随机取样平均取代了密集样点的数值积分,故计算复杂度得以降低。

联立式(16)和式(17),可估计实际噪声功率为

(18)

(19)

进一步,聚焦于期望信号区域Θs,联立式(13)、式(19),可推出期望信号协方差矩阵为

(20)

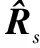
(21)

式中：α1,α2,…,αM为由大到小排序的特征值,dn是对应于αn的特征向量。从而,期望信号的方向向量可估计为

(22)

2.2 基于噪声与信号正交性的互补投影算子构造

为构造干扰加噪声协方差矩阵INCM,需消除观测空间中期望信号成分的影响,这可通过构造与信号子空间互补的投影矩阵来实现。

对式(22)的期望信号方向向量做归一化,有

(23)

考虑到实际应用中,噪声相比于干扰更具普遍存在性,因而利用噪声子空间与信号子空间的正交性,仅需从全集空间中减去信号子空间,即可构造出信号互补投影算子U,如下式所示：

U=I-BBH

(24)

从式(24)可推知,互补投影算子U的物理意义在于:从观测样本中消去其中的期望信号分量。

进而利用算子U对观测向量投影,得到

i(k)+UHn(k)

(25)

从而投影后的协方差矩阵为

(26)

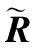
2.3 基于噪声与干扰正交性的INCM构造

构造INCM要求估计所有干扰的方向向量和对应功率。

为精确估计干扰方向向量,需做如下优化:

(27)

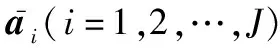
(28)

式中：μ为拉格朗日乘子,可通过求解下式得出：

(29)

(30)

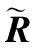
进一步利用噪声与干扰的正交性,有

(31)

联立式(30)和式(31),可推出干扰功率估计：

(32)

从而,可推出最终INCM的估计结果为

(33)

最后,根据式(22)和式(33),即可得波束形成向量：

(34)

2.4 算法总结

将以上波束形成过程归纳为算法1所示。

算法1 基于噪声子空间的波束生成器设计流程输入: 阵元个数M、阵元接收的快拍数据以及噪声采样数N步骤1 根据式(10)计算采样协方差矩阵^R,并根据式和计算残留噪声σ^2r和实际噪声σ^2n;步骤2 根据式(17)和式(18)计算期望信号协方差矩阵的估计值^Rs,进而根据式(19)和式(20),得到期望信号方向向量估计a^0;步骤3 根据式(24)构造期望信号补空间U,并根据式(26)得到准干扰协方差矩阵 R;步骤4 根据式(17)估计得到干扰方向向量的粗估计a-i=a( θi),1≤i≤J,后通过式(17)得到更准确的估计值a^i,1≤i≤J;步骤5 根据式(28)计算第i个干扰信号功率σ^2i,并根据式(32)计算自适应权值wpro。

3 仿真分析

其中,文献[12]方法求和区域、间隔分别为(-90°,θ0-5°]∪[θ0+5°,90°)和0.1°,文献[15]方法与本文求和区域为Θs,精度值为0.1°。

3.1 信号正交补投影算子的传输特性测试

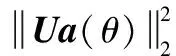
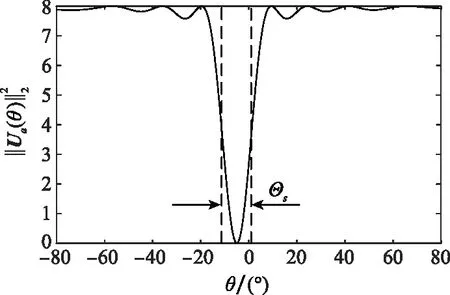
图1 信号正交补投影算子的传输曲线

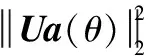
3.2 不同阵元数波束方向图对比

将本文算法应用于不同长度的线性均匀阵列(分别设定阵元个数M=8和M=12),得到的波束方向图如图2。如图2所示不同阵元数的波束方向图略有不同,阵元数为12时比阵元数为8时得到的方向图主瓣变窄,但是都在干扰角度(即-40°和20°)形成了较深的凹陷,这体现出本文方法对干扰抑制的自适应性。因而,工程实现时,需要在阵列孔径尽量大的前提下,才可以实现对近邻方向的干扰做深度抑制。

图2 不同阵元数波束方向图对比

3.3 DOA存在误差时对比试验仿真结果

令阵列个数M=8,当DOA存在+2°误差,即θ0=-3°时,仍将本文方法与以上提及的波束形成器做对比,分别观察输入SNR、快拍数对SINR的影响，结果如图3所示。图3(a)中,设定快拍数为80,设定输入SNR范围为[-10,30]dB;图3(b)中,固定输入SNR为30 dB,快拍数变化范围为[10,100]次;可看出在有DOA误差情况下,文献[5]、文献[7]、文献[10]的传输性能较差,特别是当输入SNR提高到15 dB后,SINR出现恶化,这是因为这些方法将INCM用样本协方差矩阵粗略替代。而本文在INCM构造时,做了各全面与噪声特性有关的全面考虑,故其传输曲线(以“ ☆”标记)避开了高信噪比的性能恶化效应。进一步可看出, 本方法得到的SINR曲线明显高于文献[12](以“ ◇”标记)和文献[13](以“❋”标记)的方法,这是因为这两种方法忽略了残留噪声误差带来的影响。而本文考虑了残留噪声影响的同时充分利用了子空间的相互正交特性,故输出信干燥比性能得以改善。

图3 DOA误差下性能对比

另外,还可看出本文方法得到的SINR曲线略微高于文献[15](以“□”标记)的方法,这充分反映了基于噪声特性设计的理论优越性。且本文在估计残留噪声时采用了随机取样并在构造互补投影算子U时避开了矩阵求逆过程,在性能改善的同时降低了算法复杂度,故综合实用性更高。

从图3(b)可看出,本文算法与文献[15]算法性能最好,文献[12]和文献[13]性能略差,这3种方法均仅耗费10次快拍即可得到35 dB以上的SINR输出;相比而言,文献[5]、文献[7]、文献[10]的输出SINR整体大幅下降20 dB左右,且需较多快拍数。

4 结 论

针对已有波束形成算法在高信噪比时输出下降以及计算量过大等问题,本文提出基于噪声子空间特性的波束形成器,该算法充分利用了信号、干扰和噪声空间的正交性。由于本文设计兼具低计算复杂度和高输出SINR,因而在雷达、声呐、移动通信等领域有应用前景。然而本文算法仅适用于密集阵列,未来将在稀疏阵列的波束形成器设计方面做努力。