基于正交频谱重构的微波三维成像方法

张 研, 王保平, 方 阳, 宋祖勋

(1.西北工业大学电子信息学院, 陕西 西安 710072;2.西北工业大学无人机特种技术重点实验室, 陕西 西安 710065)

0 引 言

微波三维成像技术是一种工作在300 MHz～300 GHz波段的三维合成孔径雷达(synthetic aperture radar, SAR)成像的技术[1-2],通过发射宽带电磁波信号获得距离向高分辨率,在方位向和高度向以合成孔径的方式对目标观测获得方位向和高度向高分辨率。因其具有高分辨、低辐射、非接触、三维立体成像等优点,在民用和军用领域开展了广泛的研究。在民用领域主要可应用于安检、医学诊断、灾难救援、无损检测等领域;在军用和反恐领域主要可应用于战场隐匿物体探测、重要军事目标勘察、地雷探测等领域[2-14]。

微波成像的分辨率取决于发射信号带宽、中心频率和合成孔径大小。受香农-奈奎斯特采样定律的限制,传统高分辨成像方法要求成像系统具有非常高采样率,这对雷达系统的硬件处理带来很高的难度。此外,三维成像需要在3个方向采集数据,导致回波数据量非常大,对数据处理也带来一定挑战[2,15-18]。将压缩感知(compressed sensing,CS)技术[19-20]引入微波三维成像可以大大降低成像系统的采样率和回波数据量,以欠采样数据恢复出精确的目标图像[21-23]。将稀疏度等先验知识作为约束项的正则化CS成像方法进一步提高了成像精度[24-25]。总差分(total variation, TV)正则化CS成像方法以散射点之间的能量差进行稀疏表示,可以提高成像的抗噪性能,但会降低成像精度[26-27]。为了同时提高成像精度和抗噪性能,一种基于TV和l1范数的混合约束正则化CS成像方法被提出,该方法通过迭代循环调整TV约束和l1范数约束的权值系数,实现最优的成像结果[28-30]。目前的CS成像方法主要基于目标场景的稀疏表示,由于需要计算整个目标场景最优解,导致字典矩阵的内存占用巨大,对硬件处理带来困难。此外,基于目标场景稀疏的CS成像结果是由离散的强散射点组成,对连续分布目标的细节特征体现较差,不利于目标识别。

本文首先分析了目标回波的频域空间分布特性和回波信号模型,讨论了目标回波频谱对成像的影响。然后,根据所构建的目标回波波阵面的正交投影模型实现了目标回波频谱的最优重构。最后,以成像结果的最小图像熵为判别准则对重构的正则化参数进行了最优估计,进一步提高了频谱重构精度和成像质量。计算机仿真实验和微波暗室实测实验表明,本文所提方法可以处理稀疏采样数据,内存占用较CS方法大大降低,且具有较高的成像精度,尤其对目标细节特征的恢复较为准确。

1 成像模型分析

本文所讨论的是平面扫描微波三维成像系统,采用直角坐标系表示成像几何关系,如图1所示。以目标场景中心o为坐标原点建立坐标系T(o,x,y,z),以扫描平面中心o′为坐标原点建立坐标系T′(o′,x′,y′,z),其中x′o′y′平面与平面xoy平行。雷达扫描平面的长和高分别为Lx和Ly,此即为成像系统在x′方向和y′方向的孔径长度,目标成像场景中心o与扫描平面的法向距离为z0。成像系统采用单发单收方式进行信号采集,以步进频方式发射宽频带电磁波信号,发射波瞬时频率为f=f0+Δf,f0为初始频率,Δf为频率步进间隔。

图1 成像几何模型

设rt∈R3为目标场景中心到某一散射点P的距离矢量,ra∈R3为雷达天线到目标场景中心的距离矢量,则散射点与雷达天线之间的距离矢量为

rP=ra-rt

(1)

假设电磁波传播介质为线性、各向同性、和均匀的,则在天线扫描位置(x′,y′)处接受到的散射点P(x,y,z)的反射波的电场强度标量可以表示为

E(x′,y′,x,y,z,k)=δ(x,y,z)e-jk|rP|

(2)

式中：k=4πf/c表示波数,c为光速;δ(·)表示某一位置上散射点的反射率(假设目标后向散射为各向同性的)。对于三维成像而言,可以将整个成像场景的回波近似为成像场景内所有散射点回波的线性叠加。因此,对于天线扫描位置(x′,y′),接收到的目标场景回波信号可以表示多个散射点在(x′,y′)处电场强度的积分,其表达式如下:

s(x′,y′,k)=

(3)

式中：R(x′,y′,x,y,z)表示散射点与雷达天线之间的瞬时斜距,其表达式如下:

R(x′,y′,x,y,z)=|rP|=

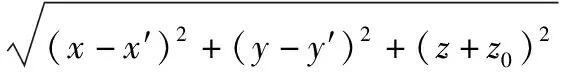
(4)

2 成像处理流程

2.1 频谱重构

对式(3)在x′方向和y′方向进行傅里叶变换,可以将回波信号变换到三维频域,其表达式如下:

s(kx,ky,kz)=

(5)

一种理想的处理方式是对上式分别在kx,ky和kz方向上进行傅里叶逆变换,即可得到目标场景的反射率分布,其表达式如下:

∭ {δ(x,y,z)e-j[kxx+kyy+kz(z+z0)]·

(6)

直接通过傅里叶逆变换运算效率太慢,一般计算机处理傅里叶变换使用的是快速傅里叶逆变换(inverse fast Fourier transform,IFFT)。IFFT要求数据具有均匀采样的格式。但在三维频域,如式(6)所示的回波信号频谱在kx-ky-kz坐标系下不具有均匀分布的性质,这是因为kz与k,kx和ky之间具有如下关系:

(7)

则式(5)变为

s(kx,ky,k)=

(8)

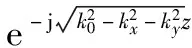
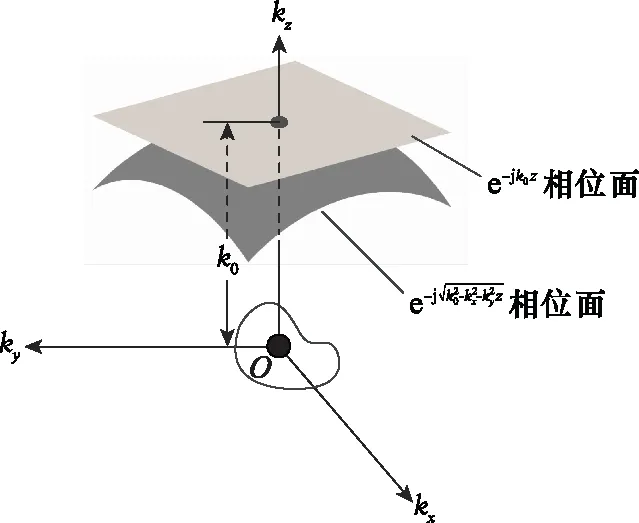
图2 相位面投影示意图

(9)

则回波频谱变为

(10)

式(10)经过IFFT就可以得到目标反射率分布。

通过变量替换实现频谱投影最常用的方法是插值,但是插值存在一定的误差和近似,而插值的过程本身也不是一个优化过程。此外,如果雷达成像系统在扫描平面和发射信号均采用随机稀疏采样的方式进行数据采集,则存在两个问题,第一个问题是数据不满足香农-奈奎斯特采样定律;第二个问题是数据为非均匀采样。这两个问题会导致原始回波数据s在x′方向和y′方向无法进行傅里叶变换,且插值精度会较差。

为了应对稀疏采样以及通过优化重构的方法实现数据的投影变换,首先需要推导由回波信号到待重构频谱之间的矩阵运算关系。设sP×Q×R为原始回波数据矩阵,P,Q和R分别为x′方向,y′方向和z方向采样点数,回波信号的频谱可以表示为以下矩阵运算：

(11)

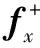
(12)

(13)

(14)

(15)

(16)

(17)

式中：λ为正则化参数,用以调节重构精度和稀疏性之间的平衡。λ的取值与先验知识相关,如待重构信号的稀疏度等。通过凸优化方法求解式(17)时,由于λ在实际应用中往往难以提前测量和估计,为了保证重构结果尽可能接近最优解,λ一般在0～1之间取较小的值。凸优化方法处理稀疏性不是很好的信号时仍能保持较高的精度,但其在处理大规模优化模型时效率太低,如三维SAR成像。因此，本文采用正交匹配追踪(orthogonal matching pursuit, OMP)算法进行重构。

在正交匹配追踪算法中,迭代终止条件依赖于对带重构信号稀疏度的估计,这将在第2.2节具体讨论。为了便于矩阵运算,将F拉伸成一维矩阵,设χλ为迭代的残差矩阵,th为判别迭代是否终止的残差阈值,t为迭代次数。具体重构流程如下所示。

算法1 目标波谱正交重构算法输入:F,Φ初始化:χλ=F,t=0迭 代:步骤1计算最大投影向量:Φη=max(ΦηF),η=1,2,…步骤2计算正交投影系数:αη=ΦTηFiΦTηΦη步骤3将重构结果填充在矩阵中:F′η=αη步骤4计算残差χλ=F-αηΦη步骤5判断:如果|χλ|≤th,停止迭代;否则,返回步骤1。 输出:F′

对F′作3D-IFFT就可以得到目标的反射率分布。

2.2 基于最小图像熵的参数优化

通过对目标频谱进行最优重构,然后再通过3D-IFFT得到目标的反射率分布(即目标图像)虽然可以在一定程度上提高成像效果,并且可以处理稀疏采样数据。但前提是选取合适的残差阈值th来判别迭代是否终止。不同的目标,不同成像环境中的杂波干扰,参数误差等都会影响最优迭代次数。因此，需要通过对残差阈值th进行最优估计。

正交投影可以消除目标频谱在kx,ky和kz方向上的耦合,使得目标精确聚焦。根据微波成像机理和信息熵理论,只有当成像参数为最优参数时,目标的聚焦性最好,此时目标图像具有最小的熵。因此，将最小图像熵作为判定准则,对正则化参数进行估计,可以求解出最优的正则化参数,并实现最优成像结果。图像熵的定义如下所示：

(18)

式中：

(19)

式中：I(x,y)为二维成像结果。由于频谱正交投影重构是逐波数采样进行的,因此只能通过对x′方向和y′方向进行IFFT得到目标的二维成像结果。在实际处理流程中对每次正交重构的残差阈值th进行调整,求出各th候选值对应成像结果的图像熵,其最小值对应的th和频谱F′就是我们所需要的最优解。为了提高计算速度,可以采用梯度下降算法或者牛顿法等进行求解。

定义imax为的采样点数,γ为迭代循环次数,ε为梯度下降算法的误差,Δth0为正交投影重构的误差阈值的初始步进值。根据最小图像熵进行参数优化的完整成像处理流程如图3所示。

图3 成像整体流程图

3 仿真与实验

本节根据平面扫描三维成像模型构建成像实验系统,分别通过计算机生成的仿真实验数据和在微波暗室测量获取的真实回波数据对本文所提方法进行验证。计算机仿真数据实验主要对所提方法的关键步骤进行定性定量分析。微波暗室测试数据主要验证本文所提方法对真实连续目标的成像效果。根据CS理论中重构字典的非相关条件,本实验所有的稀疏采样均为随机稀疏采样,采样位置的随机分布通过M序列实现。

3.1 点目标仿真分析

在计算机仿真实验中,目标如图4所示,为3个点目标,成像系统主要参数设置如表1所示。

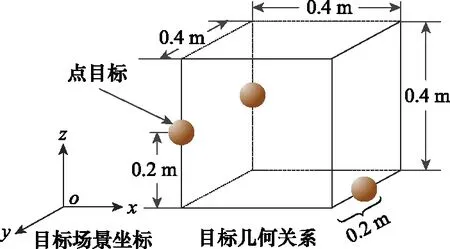
图4 点目标模型

表1 成像仿真参数

从图5(a)可以看出25%随机稀疏采样条件下传统频域插值成像方法完全散焦,说明传统频域插值方法无法处理随机稀疏采样数据。从图5(b)可以看出所提方法仅产生少量散焦情况,仍然较好地对目标的三维空间分布进行了表征。

图5 25%采样数据成像结果

频谱变换的精度对成像质量至关重要,对回波信号分别在电磁波发射方向和扫描平面进行稀疏采样,分析不同稀疏采样率下的均方误差(mean square error, MSE),如图6所示。由于稀疏重构结果与完整频谱相比会存在一些缺损,但少量缺损不影响成像,因此正交重构的MSE在计算误差时只计算非零值点。从图6中可以看出, sinc插值和非均匀快速傅里叶变换(non-uniform fast Fourier transform,NUFFT)的MSE在稀疏采样率大于70%时增长较小,在稀疏采样率小于70%时迅速增加。本文所提方法的MSE在采样率大于30%时增长比较缓慢,在稀疏采样率小于30%时迅速增加。

图6 不同数据采样率对频谱重构的影响

3.2 微波暗室测试实验分析

本研究搭建了微波暗室半物理仿真平台进行了平面扫描3D成像测试系统,测试系统如图7(a)所示。采用矢量网络分析仪、功率放大器、发射探头和接收探头来模拟一台雷达系统,模拟雷达系统放置在可升降扫描架上,扫描架被放置在一条导轨上,通过扫描架的升降和沿导轨移动实现平面扫描。测试采用逐列扫描和单发单收的方式,成像参数设置如表2所示。

表2 微波暗室成像参数

目标选用一把刀、2个矿泉水瓶、以及2个易拉罐组合成一个目标体,如图7(b)所示。这些物体被用塑料胶带固定在一个塑料泡沫支架上,刀柄和刀刃均为金属;2个矿泉水瓶的大小相同,但所装水的体积不同,左侧矿泉水装满水至瓶口,右侧大约装了3/4瓶水;2个易拉罐没有装任何物体。

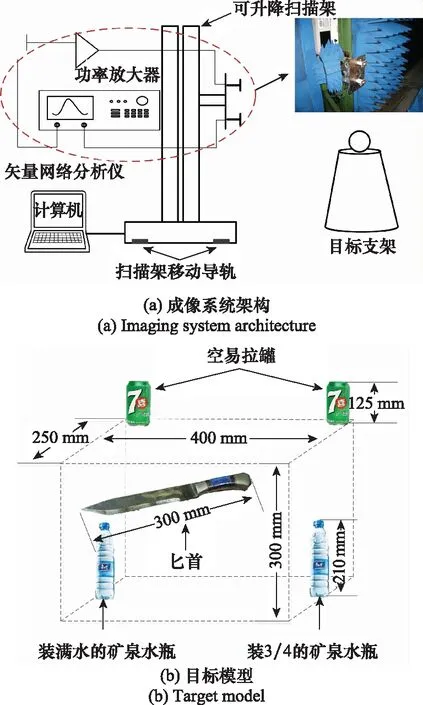
图7 微波暗室测试方案图

首先对本文所提方法在100%采样数据下的有效性进行验证,分别采用基于16点SINC插值的频域插值方法,基于OMP重构的CS成像方法,基于l1-TV重构的CS成像方法和本文所提方法,成像结果如图8所示。图8(a)为频域插值方法成像结果,由于易拉罐的反射率较低,为了显现出易拉罐的成像结果,采用图像能量峰值下降6 dB作为显示门限。从图中可以看出,刀和矿泉水瓶的成像结果存在一定变形,尤其是刀刃的尖端部分和左侧矿泉水的瓶口部分;右侧矿泉水瓶比左侧矿泉水瓶高度略低,这是因为塑料的电磁波反射能力很弱,而水的电磁波反射能力较强,成像结果实际上是瓶中的水;由于采用较低的图像显示门限,虽然易拉罐的反射能量可以显示出来,但是导致两个矿泉水瓶中间位置出现了残影。

在CS成像处理中,成像场景大小为0.6 m×0.4 m×0.4 m,成像场景离散网格化为31×21×21。分别采用了OMP算法和l1-TV重构算法。OMP成像结果如图8(b)所示,刀、矿泉水瓶和易拉罐均可以显示出来,没有旁瓣对成像结果造成干扰。但由于成像结果为离散点组成,只能体现出目标的大致轮廓,对目标形状的细节体现较差,不利于目标识别。l1-TV重构成像结果如图8(c)所示,虽然相比OMP算法提高了成像结果的连续性,但是由于算法对目标反射率进行平滑处理,降低收敛速度,使得成像结果精度下降,出现了较多杂散点。

图8 100%采样数据成像结果

图8(d)是本文所提方法成像结果。成像结果采用了图像峰值下降2 dB作为显示门限。本文所提方法成像结果与真实目标外形更加接近,可以清晰的看出刀刃尖端和左侧矿泉水瓶口的外形特征;两个易拉罐在图中清晰可见,并且几乎没有杂散点对成像结果造成干扰。

为了验证本文所提方法在稀疏采样条件下的成像能力,分别用频域插值方法、OMP重构方法、l1-TV重构方法和本文所提方法对25%稀疏采样的数据进行成像处理,成像结果如图9所示。从图9(a)可以看出,频域插值方法图像完全散焦,说明频域插值方法无法处理稀疏采样数据;从图9(b)可以看出,基于OMP重构的CS成像结果在25%稀疏采样数据下基本可以聚焦出目标形状,但发生了一定的变形,且存在少量杂散点;从图9(c)可以看出,基于l1-TV重构的CS成像结果目标图像有少量变化,但是产生了较多的杂散点;从图9(d)可以看出,本文所提方法在25%稀疏采样数据条件下,仍然可以较好的聚焦出目标形状,且相比100%采样数据条件图像质量的下降小于其他3种方法。

图9 25%采样数据成像结果

为了对实验结果进行定量分析,分别采用峰值信噪比(peak signal to noise ratio, PSNR)和结构相似度(structural similarity, SSIM)对成像质量进行分析,并比较不同算法的计算内存占用,数据采用100%采样数据,如表3所示。比较4种方法的PSNR可以看出,基于OMP重构的CS成像结果具有最高的PSNR,这是因为OMP只提取最强的若干个散射点。本文所提方法的PSNR略低于OMP重构方法,l1-TV重构方法和频域插值方法的PSNR较低,因为l1-TV重构方法和频域插值方法均存在一些杂散点,而所提方法成像结果基本无杂散点。

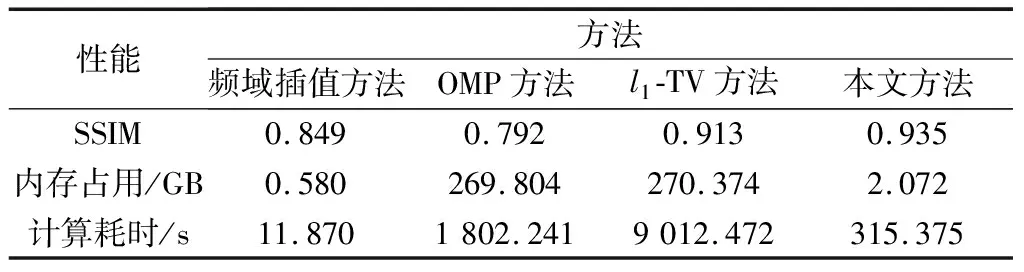
表3 成像性能对比

对于SAR成像,SSIM更能符合人眼视觉对成像效果的要求。从表3中可以看出,本文所提方法具有最高的SSIM,其次是l1-TV重构方法和频域插值方法,而OMP重构方法的SSIM最低。

分析这几种方法的内存占用可以看出,频域插值方法的占用内存最小,由于不需要构建字典矩阵,因此内存基本等于数据大小;本文所提方法占用内存略大于频域插值方法,由于本文所提方法的字典矩阵只针对每一个波数面构造,因此字典矩阵较小;OMP重构方法和l1-TV重构方法的占用内存远大于前两种方法,因为这两种方法都需要根据整个成像场景构造字典矩阵,且在三维成像模式下,字典矩阵大小会呈指数增加,严重增加硬件处理难度。

几种成像方法的计算时间差别巨大,传统频域插值方法速度非常快;OMP重构方法具有快速收敛的优点,但由于字典矩阵巨大,因而处理时间比频域插值法有大幅度增加;l1-TV重构方法收敛速度较慢,且有复杂的优化迭代过程,因此处理时间最长;所提方法通过逐次对频谱列向量进行正交重构,大幅度降低了字典矩阵大小,虽然计算时间比传统频域插值方法长,但比OMP和l1-TV重构方法具有明显减少。

图10为不同数据采样率下的成像结果SSIM曲线。从图10中可以看出在100%采样数据条件下,本文所提方法具有最高的SSIM值,之后依次是CS-l1-TV成像方法,频域插值成像方法和CS-OMP成像方法。随着数据采样率的不断下降,在100%数据采样率至30%数据采样率的区间内,本文所提方法和两种CS成像方法均保持了较好的稳定性,SSIM值下降较为缓慢;而频域插值方法的SSIM值下降非常明显;当数据采样率低于30%时,本文所提方法和两种CS成像方法的SSIM值开始出现快速下降,当数据采样率为20%时SSIM均在0.5以上,说明此时图像相比于目标出现了较大变形,但仍能基本聚焦,当数据采样率为10%时4种算法的SSIM值均小于0.4,说明此时图像已经完全散焦。结合图8,图9和图10说明本文所提方法相比于频域插值方法,CS-l1-TV成像方法和CS-OMP成像方法,与真实目标最为相似,且具有较好的稀疏采样成像能力。

图10 稀疏采样成像相似性分析

4 结 论

本文提出了一种基于正交频谱重构的微波三维成像方法,该方法采用垂直投影模型对目标的频谱进行表征,然后根据最小图像熵准则对正则化参数进行了优化估计,通过正则化稀疏重构实现了目标波谱的最优重构,最后通过对重构后的目标场景频谱做三维IFFT得到高质量的成像结果。计算机仿真实验和微波暗室测试实验表明,所提方法具有较好的稀疏采样成像能力,对目标几何结构重构较为准确,且具有较低的内存占用。