基于插值拟合的抛面共形阵盲极化DOA估计

胡毅立, 赵永波, 陈 胜, 曹成虎

(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)

0 引 言

共形阵的天线单元通过依附在载体的几何表面,增加了天线分布的自由度,并且不改变载体的空气动力学特性,极大降低了雷达的截面积,在未来战场有重要应用价值。但是共形阵面对的环境特别复杂,即使阵元间没有交叉极化,但是受到载体几何表面曲率的影响也会产生交叉极化,由于各阵元对交叉极化的贡献不同,导致极化方式和参数很难精确获得,因此共形天线阵在盲极化情况下的波达方向(direction of arrival, DOA)估计有重要的研究价值。在DOA估计方法中,除了搜索类[1-3]的DOA估计可以适用任意共形天线阵的排布以外,大多数免搜索类[4-5]算法和共形阵结合时都需要考虑天线阵的排布影响。

常见的盲极化DOA估计方法的天线结构都是基于圆柱阵[6-7]或圆锥阵[8-10],然后利用免搜索算法实现DOA的估计。圆柱阵的DOA估计方法主要是结合旋转不变技术估计信号参数(estimation of signal parameters via rotational invariance techniques, ESPRIT)的思想,选择满足旋转不变特性的子阵,由于圆柱阵的单曲率特性,可以很容易得到极化参数相同的子阵,因此圆柱阵很容易实现极化和二维角度信息解耦合[6]。借助这种思想,圆锥阵也可以选择多条母线上的天线单元,划分出极化影响相同的子阵,然后再结合免搜索DOA估计算法实现盲极化的DOA估计[8]。但是现有文献的盲极化DOA估计方法大多是基于固定且单调的母线曲率结构,鲜有针对像抛物面阵这样曲率变化的情况进行盲极化DOA估计。

本文针对盲极化共形阵DOA估计的特点,在抛物面阵中通过引入插值拟合思想,再结合ESPRIT算法,实现二维角度信息与极化参数的解耦合,实现了盲极化下的DOA估计,并且给出了盲极化下利用插值拟合思想的克拉美罗边界(Cramer-Rao bound, CRB)[11-12],最后通过仿真验证了本文算法的有效性。

1 抛面共形天线阵及插值算法

共形天线阵的形式由载体几何表面决定,在天线布阵上有很大的自由度。但是如果天线是完全任意的布阵,很容易出现遮挡、繁琐坐标转换、极化等问题[8]。不仅让共形阵信号处理变得复杂,还可能导致模糊、目标二维角度信息和极化信息相互耦合的问题,极大地影响了共形阵雷达的DOA估计。

常见的圆柱阵、圆锥阵都能很容易找到固定曲率的子阵,但是抛物面阵由于每条母线上天线单元的法线方向不一致,导致抛物面阵需考虑回波的交叉极化。图1绘制了全局坐标系下天线单元位置函数z=x2/2+y2/2的抛物面阵。

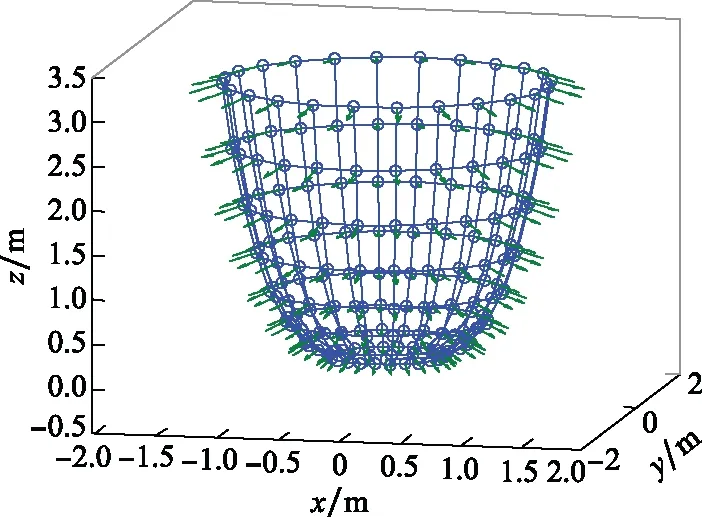
图1 抛面共形阵几何结构

其中,带有方向的短横线是天线单元的法线指向。从图1中看到每个天线单元的指向都不同,导致交叉极化的影响变得复杂,不能像常见的圆柱阵、圆锥阵那样获得极化条件影响相同的子阵,从而忽略交叉极化和目标二维角度之间的耦合。抛面共形阵的导向矢量为

a(θ,φ,γ,η)=[r1ejk0P1u,r2ejk0P2u,…,rMejk0PMu]T

(1)

u=xcosθsinφ+ysinθsinφ+zcosφ

(2)

式中：θ是方位角；φ是俯仰角;Pm是第m(m=1,2,…,M)个阵元的位置矢量;rm由第m个阵元方向图在正交基矢量uθ和uφ上的分量gm θ、gm φ，以及目标回波极化状态在uθ和uφ上的分量kθ、kφ决定,具体关系如图2所示。

图2 回波极化与阵元方向图关系

根据图2可知:

rm=|gm||ki|cosθi m=gm θki θ+gm φki φ

(3)

式中:i=1,2,…,R,R为目标个数。极化分量ki θ、ki φ由极化参数γi和ηi决定,用来体现电场矢量的正交分量之间的幅度比值和相位差值[8],且有关系式:

(4)

由于天线阵常以单个阵元自身坐标为参考,而gm θ、gm φ是全局坐标下的分量,因此阵元方向图需要全局坐标和局部坐标的转换[13],具体的转换关系流程图如图3所示。图3对应的具体步骤如下。

图3 全局坐标与局部坐标的转换关系

步骤 1.1将目标在全局极坐标下的二维角度(θ,φ)转变成全局直角坐标[x,y,z]：

(5)

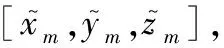
(6)

(7)

式中:Dm,Em,Fm分别是欧拉三次旋转对应的旋转角度。

(8)

(9)

(10)

步骤 2.3全局直角坐标[gm x,gmy,gm z]与全局极坐标gm(θm,φm)的关系为

(11)

通过建模过程可知,阵元的极化形式受到载体的曲率影响,表现为经过欧拉旋转变换后的极化复杂,不同阵元的极化形式多样。因此,对于抛物面阵而言,不同天线单元的极化结果不再像圆柱阵、圆锥阵那样有很强的规律性,于是未知的极化问题导致抛物面阵的DOA估计变得复杂和不确定。

插值拟合是一种经典的拟合方法[14-15],常见的形式是通过最小二乘的思想,利用插值矩阵将实际的数据矩阵转换成期望得到的数据矩阵形式。插值矩阵形式为

(12)

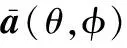
(13)

(14)

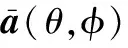
2 抛面共形阵盲极化DOA估计

2.1 基于插值拟合的盲极化DOA估计

由于抛物面阵的阵列流形可以通过插值拟合后转变成斜线阵列流形的形式,相当于变成了圆锥阵。因此，本文基于插值拟合的思想将抛物面阵拟合成圆锥阵,同时通过让插值拟合时的期望导向矢量不考虑极化信息,进而实现抛物面阵的盲极化DOA估计。

在图4(a)中体现了全局坐标系XYZ和阵元在O′处的局部坐标系X′Y′Z′之间的关系,其中Z′轴垂直于O′点处的载体横截面,X′轴平行于载体横截面。假设抛物面阵每一圈有N1个等间距分布的阵元,一条弧线(母线)上有N2个阵元,则天线单元的欧拉旋转角为

(15)

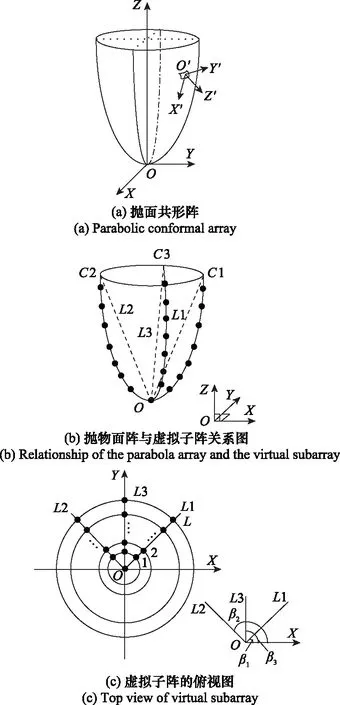
图4 基于插值拟合的抛物面阵几何关系图

(16)

式中:S是回波幅度；N1，N2，N3是3个子阵对应的高斯噪声。由于极化参数和目标二维角度耦合在一起,因此高精度免搜索的DOA估计ESPRIT方法不再适用。幸运的是借助插值拟合思想可以避免极化的影响,实现极化参数和目标二维角度的解耦合。

再对式(16)的观测区域Θ进行分块,需要考虑到极化参数(γ,η),因此对Θ的分块需要扩展成四维的划分了,具体形式为

Θ=[(θ,φ,γ,η)1,(θ,φ,γ,η)2,…,(θ,φ,γ,η)D]

(17)

式中:D=DθDφDγDη,Dθ是方位角θ的插值拟合数,Dφ是俯仰角φ的插值拟合数,Dγ是极化幅度比γ的插值拟合数,Dη是极化相位差η的插值拟合数。在实际工程应用中,(θ,φ,γ,η)的选取范围可以通过信号检测时的波位信息进行预估,确定感兴趣的大概观测区域,然后再对感兴趣的观测区域进行如式(17)所示的划分。

然后考虑到真实的导向矢量是由抛物面阵结构决定的,而为了测角方便,期望的导向矢量可以通过插值矩阵进行调整,因此可以让期望的导向矢量是圆锥阵的阵列流形形式,如图4(b)和图4(c)所示,对应导向矢量为

(18)

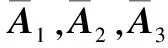
(19)

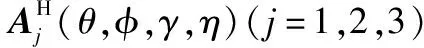
因此,经过插值拟合后的回波数据为

(20)

对应的协方差矩阵为

(21)

(22)

子阵l12上的数据为

(23)

(24)

式中:T是唯一的非奇异矩阵[16],进而

(25)

(26)

式中:Us21是Us的L+1至2L-1行数据；Us22是Us的L+2至2L行数据；Us31是Us的2L+1至3L-1行数据；Us32是Us的2L+2至3L行的数据。得到Ψ1、Ψ2、Ψ3后,再对其进行特征值分解,可得

(27)

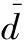
β1+β2=π,β3∈(β1,β2)

(28)

再结合式(27)可得

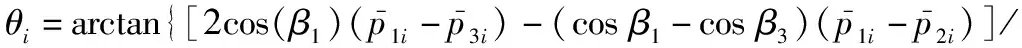
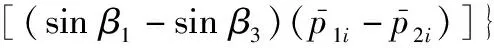
(29)

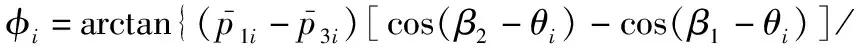
[tan(φ)(cos(β1-θi)-cos(β3-θi))·

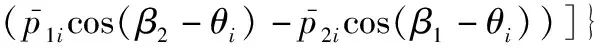
(30)

2.2 补偿插值拟合误差

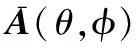
(31)

(32)

然后建立真值与补偿误差的对应关系,并且将其作为预处理的一部分。最终求解的二维DOA估计值可以表示成

(33)

需要说明的是,当目标的方位角和俯仰角都相同而极化条件不同时,不可避免存在无法完全正确补偿角度误差的情况,但是在设计插值矩阵时保证满足式(14)的约束以及式(17)对极化可能区域的覆盖,那么角度误差不一致的问题产生的影响是可以忽略的。

基于插值拟合的抛面共形阵盲极化DOA估计算法具体步骤如下。

步骤 1选取满足式(28)的3个子阵,然后获得抛物面上子阵对应的阵列流形结构。

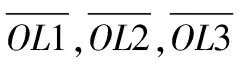
步骤 3根据式(21),获得经过插值矩阵作用后的协方差矩阵R。

步骤 4对R进行奇异值分解获得信号子空间Us,然后利用期望的天线阵结构划分出3个子阵对对应的信号子空间,再结合式(25)和式(26)得到Ψl(l=1,2,3)。

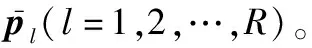
步骤 6根据式(29)和式(30)得到目标存在插值误差时的二维角度;根据式(33)获得补偿了插值误差后的方位角和俯仰角。

2.3 基于插值拟合的CRB

本节将推导多目标时多参数的CRB。由于第2.1节的方法通过插值拟合避免了极化的影响,因此经过第2.1节的插值拟合思想作用后的未知参数只有目标的方位角θ和俯仰角φ了。假定有B个目标,则协方差矩阵R中的未知参数是B个未知方位角和B个未知俯仰角。将未知参数用矢量c表示,则有

c=[θ1,φ1,θ2,φ2,…,θB,φB]T

(34)

矢量参数c的第b个参数的CRB下限为

var(cb)≥[F-1]b b

(35)

F为2B×2B的Fisher信息矩阵[11],且分块后的形式为

(36)

式中:Fθ θ是方位角的分块；Fφ φ是俯仰角的分块。F的第bi行第bj列值为

(37)

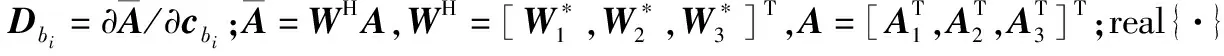
3 仿真分析

为了比较所提方法的有效性,本节通过蒙特卡罗实验仿真了检测概率与信噪比(signal to noise ratio, SNR)的关系;插值拟合误差补偿前后的角度估计差异;SNR、脉冲数变化时与均方根误差(root mean square error, RMSE)的关系。其中二维DOA估计的RMSE的定义为

(38)

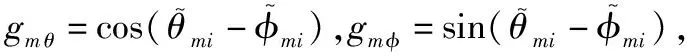
图5 检测概率随着SNR变化的情况

在图5中实线是补偿了插值误差后的图形,而虚线是没有补偿插值误差后的对比结果。从图5中可以看到,在补偿了插值误差后的检测概率明显比没有补偿的检测概率高。在高SNR时噪声误差可以忽略,此时检测概率主要由插值误差决定,然后对比补偿前Δ=2°和Δ=3°的曲线,可以发现插值误差导致的二维DOA估计误差在2°～3°之间,而通过补偿算法可以有效弥补DOA估计误差,极大提高了目标的检测概率。

图6仿真了SNR=15 dB时二维目标的散点图。经过统计,插值误差在补偿前是1.60°,补偿后是0.62°,说明所提的补偿算法对二维DOA估计有较大提升。

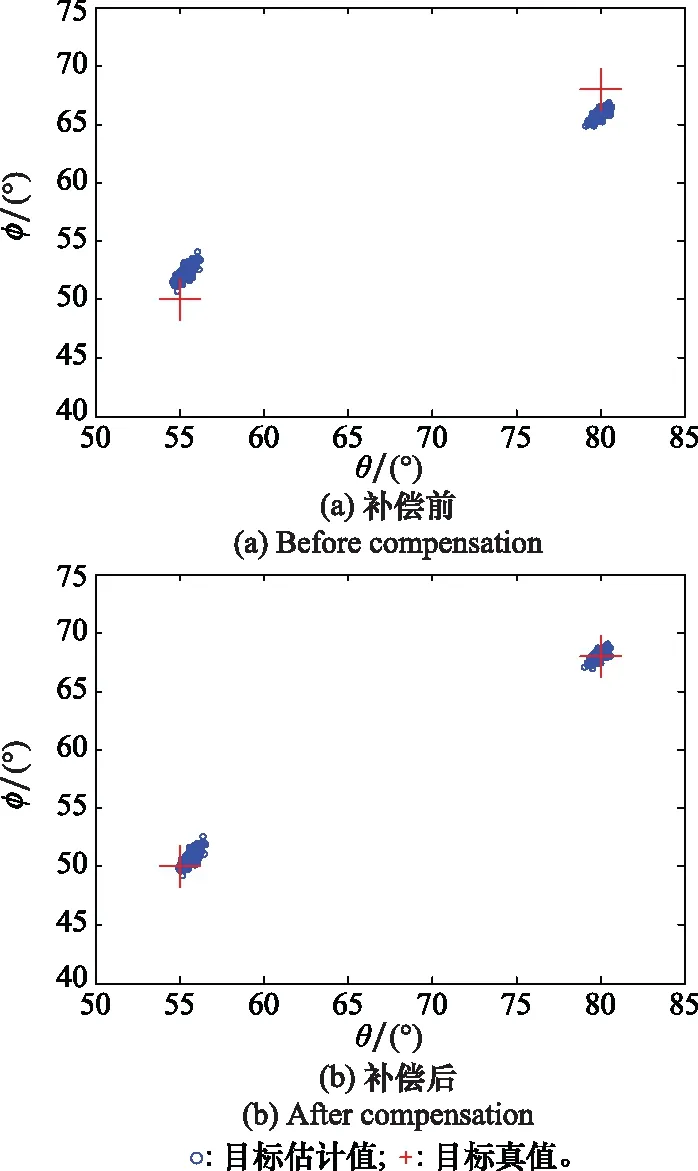
图6 二维目标的散点图

在抛物面阵天线结构、阵元方向图、插值拟合后的子阵结构都不变的情况下,假定目标仍然是两个,对应的(θ,φ,γ,η)分别为(75°,55°,35°,45°)和(85°,65°,45°,50°),插值拟合门限值δ′=0.15,按照第2.2节的设计步骤重新设计插值矩阵及补偿角度后,仿真了二维DOA的RMSE与SNR的关系图,如图7所示。从图7中可以看到在低SNR时所提方法的RMSE和理想的CRB曲线相比有很大的损失,这是由于此时不仅有噪声导致的测角误差,还有插值拟合导致的测角误差联合影响测角精度。而在高SNR时只用考虑插值拟合的误差,所提方法由于补偿了插值损失使性能有明显改善。

图7 RMSE与SNR的关系

接下来分析存在插值拟合误差时随着脉冲数的变化对二维测角RMSE的影响。在图8中仿真了SNR分别取10 dB,15 dB,20 dB,25 dB时随着脉冲数变化的RMSE图形。

图8 RMSE与脉冲数的关系

图8中虚线对应补偿前,实线对应补偿后。从图8可知在高SNR时只有插值拟合误差需要考虑,此时随着脉冲数的变化,补偿了插值拟合损失的RMSE比补偿前有明显提升,说明第2.2节所提的补偿方法能有效提高DOA估计精度。

本文方法是将4个未知参数的抛物面阵列流形拟合成两维的圆锥阵列流形,虽然损失了目标的极化信息,但是保留了目标参数估计时最重要的二维角度信息。同时由于本文算法的插值矩阵是预处理过程,不占用实时处理计算量,因此本文算法的计算复杂度和常规的圆柱阵、圆锥阵DOA估计情况并无差别。

在插值拟合时,为了保证拟合后的插值误差不会过大,期望拟合的阵列流形选择了和抛物面阵结构最接近的圆锥阵。但是为了实现盲极化测角而在期望阵列流形中不考虑极化信息,将不可避免增大拟合误差的影响,特别是在低SNR时,RMSE结果受到了噪声和插值拟合误差的联合影响,导致在低SNR时的RMSE偏大,而在高SNR时通过补偿方法弥补了插值拟合损失,因此高SNR时DOA估计精度有明显提升且接近CRB值。

4 结 论

本文分析了抛物面阵的结构特点以及交叉极化对DOA估计的影响,提出了基于插值拟合的抛面共形阵盲极化DOA估计方法,通过插值矩阵实现了将抛物面阵的四维阵列流形拟合成只有方位角和俯仰角的二维圆锥阵列流形,然后结合ESPRIT方法实现了二维DOA估计,并且估计的二维角度能够实现自动配对。考虑到拟合误差对测角精度的影响,设计了一种补偿插值拟合损失的方法提高了DOA估计精度,最后给出了本文模型的CRB结果。

通过仿真实验发现本文方法在极化参数未知的情况下,能有效地估计抛面共形阵的目标二维DOA信息,特别是高SNR时,测角精度接近CRB。但是在低SNR时受到噪声和插值拟合误差的联合影响,导致低SNR时RMSE偏大,因此如何提高在低SNR时的DOA估计精度将是后续研究工作的重点。