最简多磁偶极子等效建模方法

金煌煌, 庄志洪, 付梦印, 郭 健, 王宏波

(1.南京理工大学自动化学院, 江苏 南京 210094;2.南京理工大学电子工程与光电技术学院, 江苏 南京 210094)

0 引 言

随着潜艇静音技术的不断进步,目前大多数潜艇潜航噪声已经接近甚至低于海洋背景噪声水平,单纯利用声呐探测已经不能满足现代反潜作战的需求。航空磁探技术具有探测范围大、执行时间短、不受海洋复杂环境影响等优点,西方认为其是当今提高对潜攻击最可靠的非声探测手段。以美军P-3C、P-8A反潜机为代表,其上均搭载了高精度的磁异常探测装备,磁异常探测已经成为水下目标探测的重要手段[1-4]。随着反潜作战目标环境的日益复杂,如目标类别日趋增多、无人水下航行器(unmanned underwater vehicle,UUV)潜艇模拟器的大量应用,以往应用较为广泛的基于远场单磁偶极子模型的磁异常定位方法,由于单磁偶极子模型没有充分利用潜艇磁异常信号的全部信息,其中包含磁目标磁分布特性、结构特征、运动参数等特征信息量较少,已经不能完全满足水下目标识别与分类任务的需要。先进的磁异常探测系统应具有从水下潜艇目标探测定位进一步扩展到包括UUV、鱼雷、水雷等在内的目标探测和识别能力,甚至包括磁诱饵目标[5-8]。

针对多磁源目标的反演和识别有赖于建立包含目标结构分布信息的高精度磁场模型。对于舰船目标,常用的高精度磁场模型包括等效法模型、均匀磁化的旋转椭球体阵列模型、均匀磁化的旋转椭球体与磁偶极子阵列混合模型[9]以及基于三维有限元法的数值模型等[10-13]。在工程应用中,有限元法存在计算量大、空间磁场分布实时获取困难等问题;而上述其余模型均是基于磁体模拟法的思想,磁体模拟法是用若干具有特定磁矩的磁源所产生的磁场来模拟舰船磁场[14],磁体模拟法也面临一些问题:① 大型舰船磁场分布数据难以通过现场测量的手段获取;② 为建立高精度磁场模型,一般通过增加磁源数提升模拟精度,而磁源数的增加同时也带来了计算机拟合计算量的增加,不利于等效方程的求解[15]。此外,针对磁体模拟法中磁源的磁矩方向、大小、分布的确定问题,目前尚未形成明确有效的方法体系。

本文针对上述磁体模拟法目前存在的问题,开展了不同空间尺度条件下等效磁偶极子个数、分布、磁矩大小方向对测平面上磁场分布等效效果的影响研究,给出了多磁偶极子最简等效模型建立依据,并以国外某型潜艇模型为例,利用COMSOL多物理场仿真软件对最简模型等效效果进行了评估,验证了最简模型的有效性。

1 磁体模拟法的理论基础

从物质的原子结构观点来看,铁磁质内电子间因自旋引起的相互作用是非常强烈的,在这种作用下,铁磁质内部形成了一些微小的自发磁化区域,叫做磁畴。磁畴是指铁磁体材料在自发磁化的过程中为降低静磁能而产生分化的方向各异的小型磁化区域。磁畴结构是铁磁质的基本组成部分[16-17]。

当铁磁体处于原始退磁中性状态时,由于铁磁体内各个磁畴的磁化矢量取在不同的方向上,所以在宏观上对外不显示磁性[18-19]。当铁磁体处于外磁场中时,那些自发磁化方向和外磁场方向成小角度的磁畴其体积随着外加磁场的增大而扩大并使磁畴的磁化方向进一步转向外磁场方向。另一些自发磁化方向和外磁场方向成大角度的磁畴其体积则逐渐缩小,这时铁磁质对外呈现宏观磁性。当外磁场增大时,上述效应相应增大,直到所有磁畴都沿外磁场排列达到饱和。由于在每个磁畴中各单元磁矩已排列整齐,因此具有很强的宏观磁性[20-21]。

由上述磁畴理论可知,铁磁体在磁化空间中的磁感应场分布是由铁磁体内部一系列磁畴的磁感应场分布叠加形成。磁畴的体积形状分布与材料的微观性质密切相关,对微观结构的磁畴来说,在一定测高范围内,其磁感应场分布都可以由磁偶极子的磁感应场分布等效。而多个磁畴的叠加磁感应场可用已知磁感应场分布的磁性物体来等效,该方法称之为磁体模拟法或等效磁源法。对舰船磁感应场来说,常用的磁性目标磁场建模磁体模拟模型有:旋转椭球体模型、磁偶极子阵列模型、旋转椭球体与磁偶极子阵列混合模型[22-25]。

2 等效磁偶极子阵列磁矩分布对等效效果的影响

2.1 空间尺度定义

实际工程应用中,磁偶极子阵列模型相较于其他两种模型在模型计算复杂度上大幅降低,同时在远距离磁场分布等效时具备较好的等效精度。目前,磁偶极子阵列模型中磁偶极子的个数选择、磁矩大小和方向的确定以及磁偶极子的分布等对铁磁体磁场分布等效效果的影响尚无较为系统的研究和成熟的理论。

对铁磁体磁场分布的等效效果的研究分析是建立在特定的测高平面和铁磁体的结构尺寸上的,因此本文提出空间尺度的概念,即定义空间尺度α=H/LT,其中H为测平面高度,LT为铁磁体或磁偶极子阵列的最大结构尺寸。

2.2 多磁偶极子等效模型磁矩方向的选择

潜艇等舰船目标一般都由高强度合金钢制成,其外壳属于铁磁性物质,在加工和制造过程中,材料内部应力的反复变化、温度的升降变迁以及局部地磁场的影响,都会引起铁磁材料内无磁滞磁化的形成,归结为目标的永久磁场[26]。永久磁场的形成是铁磁材料的静态磁化过程,其内部磁畴的磁化主要包含磁畴壁的位移磁化过程和磁畴转动磁化过程。畴壁位移磁化指的是在外磁场作用下,自发磁化方向接近于外磁场方向的磁畴长大,而自发磁化方向与外磁场方向偏离较大的近邻畴相应地被压缩,使畴壁发生位置变化;磁畴转动磁化过程是铁磁体在外磁场作用下,其磁畴内所有磁矩一致向着外磁场方向转动的过程[27]。

因此,在利用多磁偶极子等效模型进行舰船等目标磁场等效时,由磁畴磁化理论可知,其内部绝大多数磁畴最终将趋于和外磁场方向一致,即等效磁偶极子磁矩方向可选取排列一致的磁化方向。

2.3 磁偶极子磁矩大小、分布的最简等效条件

多磁偶极子最简等效条件即寻求在特定空间尺度条件下,用最少个数的磁偶极子组合等效目标铁磁体空间磁场分布。首先考虑两个磁偶极子等效成单磁偶极子的等效条件。单磁偶极子在空间某测点处产生的磁感应强度B为

(1)

式中:μ为相对磁导率；M为单磁偶极子的磁矩矢量；r为空间测点相对单磁偶极子的相对位置矢量。如图1所示,使磁偶极子M1、M2在空间某测点处产生的磁感应强度B1和B2叠加后与单磁偶极子M0产生的磁感应强度B0等效,需满足矢量叠加原理:B0=B1+B2。

图1 2个磁偶极子与单磁偶极子的等效示意图

测点处于无限远时,r1=r2=r0,此时2个磁偶极子与单磁偶极子等效需满足:

(2)

可得等效条件为M0=M1+M2,即两个磁偶极子等效成单磁偶极子的磁矩条件为两个磁偶极子磁矩方向与单磁偶极子保持一致,磁矩大小之和等于单磁偶极子磁矩大小。

两个磁偶极子磁矩大小的分布决定着等效单磁偶极子的相对位置,在相对大空间尺度条件下研究其影响规律。用一条等高测线上各测点处,两个磁偶极子叠加磁感应场之和与单磁偶极子磁感应场各分量等效均方误差对等效效果进行量化评估。假设两个磁偶极子磁矩大小之比M2/M1=3,分别位于(-1,0,0)和(1,0,0)处,测线坐标为(x,0,z),x∈(-∞,+∞),相对空间尺度取10,则磁感应场三分量的等效效果分别为

(3)

(4)

(5)

等效单磁偶极子位置与磁感应强度等效均方误差对应关系如图2所示,磁感应场三分量具有和位置一致的对应关系。且等效单磁偶极子在两个磁偶极子连线上的位置分布与磁矩大小分布具有同比例关系(磁矩比例为3∶1,等效单磁偶极子位于连线3/4处时其等效误差趋近于0)。

图2 等效单磁偶极子位置分布与等效误差的关系(磁矩比例为3∶1)

为进一步确定两个磁偶极子磁矩不同比值条件下,等效单磁偶极子位置的分布规律,假设磁矩大小比例从0.1不断增大到10,获取等效单磁偶极子位置即等效误差最小位置,如图3所示。图3中拟合曲线为x0=(p-1)/(p+1),其中p=M2/M1,即等效单磁偶极子位置满足与2个磁偶极子磁矩大小分布同比例关系。

图3 等效单磁偶极子位置与双磁偶极子磁矩大小比值的关系

2.4 相同磁矩大小的多磁偶极子对单磁偶极子磁场分布等效一致性

为确定2个磁偶极子在特定空间尺度下具备最简等效的有效性,分别在不同的空间尺度下,对2个和3个磁偶极子与单磁偶极子的测平面磁场分布等效效果进行计算评估。等效效果用测平面上各测点的磁感应场总场值的平均绝对百分比误差(mean absolute percentage error, MAPE)来定量评估,将等效一致性(equivalent consistency, EC)定义为EC=1—MAPE。

多个磁偶极子在空间测点处的磁感应强度即为每个磁偶极子在空间测点处的磁感应强度矢量叠加,磁感应强度总场为磁感应强度矢量的模。

(1)2个磁偶极子与单磁偶极子等效一致性

2个磁偶极子磁矩大小分别取单磁偶极子磁矩大小的一半、磁矩方向与单磁偶极子磁矩方向一致,单磁偶极子位于2个磁偶极子分布中心,空间尺度分别取0.5、1、3、4(即测平面高度分别为2个磁偶极子间距的0.5、1、3、4倍)时,2个磁偶极子产生的磁感应场总场分布和单磁偶极子总场分布图以及等效一致性结果如图4所示。

图4 不同空间尺度下两个磁偶极子与单磁偶极子的磁总场分布

(2)3个磁偶极子与单磁偶极子等效一致性

3个磁偶极子磁矩大小分别取单磁偶极子磁矩大小的1/3、磁矩方向与单磁偶极子磁矩方向一致,单磁偶极子位于3个磁偶极子分布中心,空间尺度分别取0.5、1、3、4时,3个磁偶极子产生的磁感应场总场分布和单磁偶极子总场分布图如图5所示,不同空间尺度下2、3个磁偶极子的等效一致性结果对比如表1所示。

图5 不同空间尺度下3个磁偶极子与单磁偶极子的磁总场分布

表1 不同空间尺度下2、3个磁偶极子与单磁偶极子磁总场等效一致性对比

由上述结果可以得到以下结论:

(1)大空间尺度条件下,多磁偶极子阵列对单磁偶极子磁感应场分布等效时磁矩方向与单磁偶极子磁矩方向一致;

(2)2磁偶极子对单磁偶极子等效时,2磁偶极子磁矩大小之和等于单磁偶极子磁矩大小,且等效单磁偶极子位置分布受2个磁偶极子磁矩大小分布等比影响;

(3)等效磁偶极子数越多等效精度越高,2个磁偶极子已经具备较高的等效一致性,空间尺度大于3后等效一致性差异不大。

进一步对两个磁偶极子等效一致性的下界进行分析。在满足上述等效结论的前提下,单磁偶极子磁矩方向取随机方向,2个磁偶极子大小分布取随机分布,以等效一致性大于99%为最低等效条件,满足上述随机条件的100组仿真结果如图6所示,结果表明,2个磁偶极子空间磁场分布与单磁偶极子空间磁场分布等效下界为空间尺度不小于3,即在任意等效磁矩大小、方向下,当空间尺度大于3时,2个磁偶极子与单磁偶极子空间磁感应场分布等效一致性均大于99%。

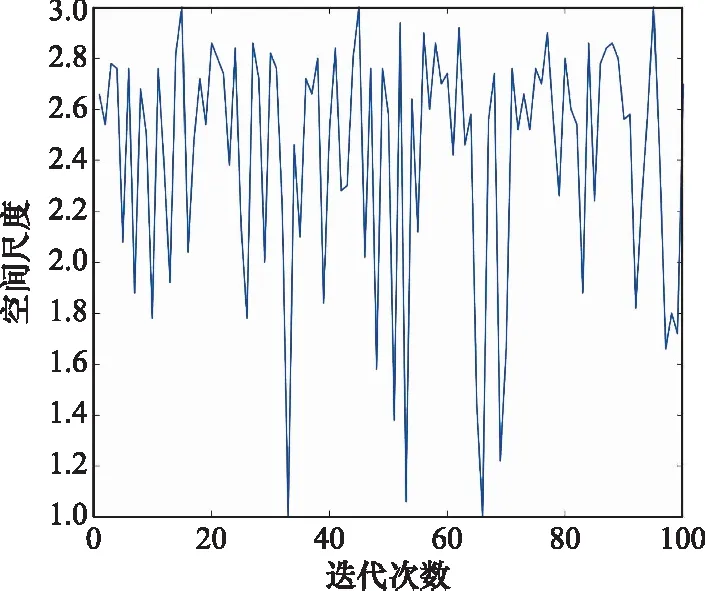
图6 等效一致性下界分析

更多的仿真结果表明:空间尺度大于等于3的条件下,同样满足等效单磁偶极子位置与2个磁偶极子磁矩大小分布同比例,且单磁偶极子的磁矩大小等于2个等效磁偶极子磁矩大小之和的等效关系。

2.5 多磁偶极子阵列最简等效条件

采用磁体模拟法进行铁磁体等效时,一般采用大量椭球体或磁偶极子组成的阵列以提高等效精度,由上述仿真结果可知,在相对大空间尺度条件下,较少数量的磁偶极子阵列具备和较多数量的磁偶极子阵列近似的等效一致性,因此需要研究不同空间尺度条件下的多磁偶极子阵列的最简等效组合,以降低等效磁矩大小及分布的计算复杂度。

以位置均匀分布的8个磁偶极子阵列为研究对象,取测高为该阵列的线长,即空间尺度小于等于1(此时磁偶极子阵列等效的铁磁体长度大于阵列的线长)。分别对磁矩大小不同分布的两种典型情况下测平面磁总场分布进行仿真,如图7所示。

图7 磁矩大小不同分布的8磁偶极子阵列测平面磁总场分布图

仿真结果表明,当空间尺度为1时,八磁偶极子阵列模型在测平面上的磁总场分布最多呈现出两个磁偶极子分布的分辨率。更多的仿真表明,无论磁偶极子阵列所含磁偶极子数多少,其在空间尺度为1条件下的测平面磁感应场分布最多呈现两个磁偶极子分布的分辨率。即无论线阵上有多少个磁偶极子,在空间尺度约为1进行等效时,由于磁偶极子的相互影响(即上文中论述的当测高大于两个磁偶极子间距时，其磁场空间分布可等效为单磁偶极子),仅有两端的磁偶极子有显著贡献。空间尺度大于3时,进一步简化为单磁偶极子。而对于空间尺度小于1的测面,这种相互影响较弱,空间尺度越小,呈现的磁偶极子分布数增加。

为进一步明确多磁偶极子阵列最简等效条件,假设一位置均匀分布的多磁偶极子阵列模型含磁偶极子个数为2N,磁偶极子间距为L,则阵列线长为(2N-1)L,测高H取与线长等值,如图8所示。

图8 多磁偶极子阵列示意图

假设多磁偶极子个数为4,如图9所示,由于测高H=(4-1)L=3L满足等效所需的测高条件,进行一次等效成两个磁偶极子后,两个磁偶极子间最大可能的间距为3L,故此时测高和间距相等,无法满足继续往上等效的条件。同理可知,特定空间尺度条件下的多磁偶极子阵列最简等效条件,即求多磁偶极子阵列无法满足继续下一次等效的条件时,最后一次可等效的磁偶极子阵列所含磁偶极子个数。

图9 多磁偶极子阵列逐层等效示意图

由上例可推,当空间尺度为1时,2N个磁偶极子经过M次等效之后,磁偶极子间间距最大可为(2M-1)L,则多磁偶极子阵列最简等效条件需同时满足(2N-1)L≥3(2M-1)L和(2N-1)L≤3(2M+1-1)L,M取整可得M=N-2。因此,空间尺度为1时,无论N取多大,其最简等效模型均为4磁偶极子阵列。

综上,可知空间尺度较小条件下,多磁偶极子最简等效条件如下:当空间尺度为1～3时,最简等效磁偶极子数为4;当空间尺度为1/3～1时,最简等效磁偶极子数为8,当测高与铁磁体宽度比值满足相应关系时同样依次类推。磁偶极子位置采取均匀分布,大大降低了等效计算的复杂度,磁矩方向与大空间尺度条件下磁偶极子等效磁矩方向一致。

3 COMSOL仿真软件获取潜艇磁感应场空间分布

如前所述,磁体模拟法存在的另外一个问题是,大型舰船磁场分布数据难以通过现场测量的手段获取。针对求解潜艇磁感应场问题,COMSOL Multiphysics AC/DC 模块以有限元法为基础,通过求解如下静磁场基本方程,并利用磁屏蔽特征以及外部对磁化场绝缘建立边界条件,可以获取潜艇在已知地磁场背景场条件下的磁感应场空间分布。

在无电流区域,静磁场的基本方程如下:

(6)

定义磁标势Vm满足:

(7)

利用磁感应强度与磁场强度之间的本构关系:

B=μ0μrH

(8)

以及

(9)

可以得到磁标势Vm的方程

(10)

对于潜艇磁感应场,其背景场为已知地磁场,则需要求解的微分方程为

(11)

式中:Be为背景地磁场。

以国外某型潜艇为研究对象,建立其几何模型,背景地磁场矢量、外壳厚度、材料相对磁导率尽可能按真实情况给定,潜艇模型及其在不同测平面上的磁总场分布如图10和图11所示。

图10 COMSOL建立的某潜艇模型

图11 潜艇磁感应场空间分布示意图

从COMSOL仿真结果可以看出,随着空间尺度的不断减小,潜艇磁矩分布特征也逐渐突出,与前述结论一致,表明在越小的空间尺度下需要越多的磁偶极子数进行潜艇磁感应场分布的等效。

4 基于COMSOL潜艇磁感应场分布的多磁偶极子最简等效模型验证

特定空间尺度下铁磁体多磁偶极子最简等效建模方法主要包括以下步骤:

步骤 1利用大空间尺度测平面的磁感应场数据,求解远场单磁偶极子模型的磁矩矢量;

步骤 2由测平面高度确定及铁磁体的尺寸,确定铁磁体三维(长宽高)空间尺度;

步骤 3依据多磁偶极子最简等效条件,对确定空间尺度下对应位置均匀分布的最少个数多磁偶极子模型,由测平面的磁感应场数据,求解各个磁偶极子的磁矩大小。

如图12所示,对于潜艇这种形状不完全规则的铁磁体,参照其形状特征,取其长轴方向上的中心点为原点,其远场等效磁偶极子位置为(x0,0,0),磁矩矢量M=(Mx,My,Mz),则由式(1),在测平面上获取两个以上已知测点坐标的磁感应场矢量值,建立方程组如下,即可采用L-M(levenberg-marquardt)算法对上述4个未知数求解从而获得单磁偶极子模型的磁矩矢量,本文中利用1stOpt最优化拟合软件进行参数求解。

图12 潜艇近远场磁偶极子模型与测点关系示意图

(12)

式中:i=1,2,…;ri=(rix,riy,riz)为各测点相对单磁偶极子模型的位置矢量;Bi=(Bix,Biy,Biz)为各测点Qj测得的磁感应强度矢量。由COMSOL潜艇模型求解得到其远场单磁偶极子磁矩矢量为

M=(1.875 4×106,-6.651 2×104,1.347 2×105)Am2

在空间尺度为1的测平面上获取该潜艇模型的磁感应强度分布,由于该潜艇另外两维结构尺寸远小于测高,故建立最简4磁偶极子模型如图12所示,其中各磁偶极子在位置上沿长轴均匀分布,磁矩方向与远场单磁偶极子模型磁矩方向相同,因此4个磁偶极子磁矩矢量满足

(13)

只需求解3个独立未知数,即可获得空间尺度大于等于1情况下的潜艇最简多磁偶极子模型。

潜艇在空间尺度为1的测平面上测点Qj(xj,yj,zj)处的磁感应强度矢量为Bj=(Bjx,Bjy,Bjz),则根据磁矢量叠加建立等效方程组如下：

(14)

式中:rij=(rijx,rijy,rijz)为测点Qj相对第i个磁偶极子Dj的相对距离。

为评估此最简多磁偶极子模型的等效效果,取空间尺度大于等于1的多个测平面数据与模型计算数据进行比较。如图13所示,分别在空间尺度为1和2时,给出由最简多磁偶极子模型计算和COMSOL潜艇模型计算得到的测高平面上的总场分布,另由电磁场的唯一性定理可知,求解电磁场的定解问题时,只要满足给定的控制方程和边界条件,其解必定唯一[28]。结合最简多磁偶极子模型在多个空间尺度上的等效一致性如图14所示。可以看出,空间尺度为1的条件下建立的4磁偶极子最简模型，具备在空间尺度大于等于1时空间多尺度条件下的高等效一致性,且等效一致性随着空间尺度的增大而提高,充分满足电磁场的唯一性定理。

图13 最简多磁偶极子模型和COMSOL潜艇模型计算的总场分布图

图14 空间多尺度条件下最简多磁偶极子模型等效一致性

5 结 论

大型舰船的消磁、基于磁场测量的目标识别分类等任务,离不开对目标磁场分布的精确建模,磁体模拟法作为解析等效建模方法一直存在着等效计算量大的问题。本文通过研究不同空间尺度下磁偶极子个数、分布、磁矩大小方向等对等效一致性的影响,系统性地提出了空间多尺度条件下多磁偶极子最简等效建模方法。利用COMSOL多物理场仿真软件获取潜艇空间磁场分布,对建模方法进行了验证评估,确认了该方法的有效性,为相关研究奠定了理论基础。