基于RSAMP算法的OFDM稀疏信道估计
季 策, 王金芝, 李伯群
(1.东北大学计算机科学与工程学院, 辽宁 沈阳 110169; 2.东北大学医学影像智能计算教育部重点实验室, 辽宁 沈阳 110169; 3.辽宁科技大学电子与信息工程学院, 辽宁 鞍山 114051)
0 引 言
正交频分复用(orthogonal frequency division multiplexing, OFDM)技术是无线通信系统中普遍应用的重要技术之一,对于OFDM系统而言,相关检测、解调、均衡等技术都需要精准的信道状态信息[1](channel state information, CSI)。而对于CSI的获取,信道估计技术尤为关键。因此,信道估计是无线通信系统中主要研究方向之一,信道估计的结果可直接影响整个通信系统性能。传统的用于解决信道估计问题的方法如最小二乘估计方法和最小均方误差估计方法[2-3]是事先假定无线信道为密集型而提出的估计方法,没有考虑到无线信道原有稀疏性,因此信道估计需要借助大量的导频信号完成。而且,传统的信道估计方法的性能并不理想。
压缩感知(compressed sensing, CS)[4-6]的出现,带来了一项获取和处理信号的新技术,可以实现对可压缩的信号以远小于奈奎斯特速率的方式采样,最终以较少的采样值高概率准确地重构出原始信号。目前无线通信系统逐渐宽带化,大量研究表明无线信道展现出较强的稀疏特性[7],加之CS理论的成熟和完善,其在无线通信领域的应用越发广泛。通过对比传统的和基于CS的信道估计方法发现,后者能够以较少的导频获得较好的估计性能。目前应用较广泛的基于CS的信道估计方法有正交匹配追踪(orthogonal match pursuit, OMP)算法[8-9]、子空间(subspace pursuit, SP)算法[10-11]、分段正交匹配追踪(stagewise orthogonal match pursuit, StOMP)算法[12-13]和广义正交匹配追踪(generalized orthogonal match pursuit, GOMP)算法[14-15]。上述算法的重构精度较高且易于实现,但是要想利用其进行信道估计必须提前知道信道的稀疏度,然而现实应用中信道的稀疏度均是不可知的,所以上述算法在现实应用的信道估计问题中并不适用。关于稀疏度不可知的问题,在稀疏度自适应匹配追踪(sparsity adaptive match pursuit, SAMP)算法[16]提出后得到了解决,其不需要提前获知稀疏度,而是通过步长的方式逐步扩大支撑集来接近真实稀疏度,自适应地完成信号的重构。2018年,文献[17]提出了一种稀疏度自适应贪婪迭代(sparsity adaptive greedy iterative, SAGI)算法,该算法设计了一种新的稀疏度估计方法,避免了稀疏度的欠估计问题。改进之后的算法不需要提前获知稀疏度,且相比于SAMP算法提高了重构效果,降低了运行时间。但是由于预测稀疏度和确定迭代方向时步长取值过小,导致运行时间降低的幅度比较小。
针对OFDM系统信道稀疏度未知的情况以及SAGI算法存在的缺点,本文提出了一种基于有限等距性质(restricted isometry property, RIP)的稀疏度预测自适应匹配追踪(RIP based prediction-sparsity adaptive matching pursuit, RSAMP)算法。首先利用提出的稀疏度过估计判据,降低了稀疏度预测的运行时间、提高了稀疏度预测的准确性;其次对算法观测矩阵进行了优化处理,通过降低观测矩阵的相干性提高了算法的重构性能。仿真结果显示,对于OFDM系统信道估计,本文的RSAMP算法相比于SAMP、SAGI算法有更好的估计性能,且运行速度更快。
1 OFDM系统模型
本文考虑具有N个子载波和P个导频子载波的OFDM系统,用X表示发送端发送信号,用Y表示接收端接收信号,则Y可以表示为
Y=XH+n=XWh+n
(1)
式中:X=diag(X1,X2,…,XN)是N×N维矩阵;H=[H(1),H(2),…,H(N)]是N×1维向量,为信道频域的响应值;n=[n(1),n(2),…,n(N)]是N×1维向量,为高斯白噪声;W是N×L维矩阵,为DFT矩阵的子矩阵,其中L是信道长度。
设S为P×N维的选择矩阵,利用S从接收信号Y中选择导频信号,则导频信号为
YP=XPWPh+nP
(2)
式中:Yp=SY是P×1维向量;XP=SXST是P×P维矩阵;WP=SW是P×L维矩阵;nP=Sn是P×1维向量。对于接收端而言,Yp,XP,WP均为已知信号,因此向量h的估计等价于稀疏信号的重构,可以利用CS重构算法重构向量h,然后通过式(1)求解出信号频域响应值H。向量h的估计[18]具体描述为
y=Φh
(3)
式中:y=YP是观测向量;Φ=XPWP为观测矩阵。
2 SAGI算法
传统的SAMP算法通过步长s逐步接近信号稀疏度以完成信号的重构,虽然无须稀疏度先验消息,但是步长s的选择会对算法的重构精度和时间带来较大的影响,若s取值较小,则算法需要进行大量的迭代,进而增加了重构时间;若s取值较大,则导致稀疏度的估计值与真实值之间的差异过大,进而降低了重构精度[19-20]。SAMP算法的主要实现步骤如下。
步骤 1输入观测矩阵Φ,测量向量y,步长s。
步骤 2初始化稀疏度r0=y,步长L=s,支撑集T0=∅,迭代索引n=1。
步骤 3通过式u=|〈Φ,r〉|计算相关系数,并从u中取出最大的L个值对应的索引存入索引集Fn,并更新候选集Cn=Tn-1∪Fn。


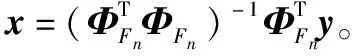
2018年,针对SAMP算法存在的不足,文献[17]提出了SAGI算法,通过新的稀疏度估计方法可以获取较精确的初始支撑集和残差,提高了算法重构的成功率,并适当减少了算法的运行时间,SAGI算法的具体实现步骤如下。
步骤 1输入观测矩阵Φ,测量向量y。
步骤 2初始化稀疏度K0=1,索引集F0=∅。
步骤 3通过式u=|〈Φ,r〉|计算相关系数,并从u中取出最大的K0个值对应的索引存入索引集F0。

步骤 5在K0-和K0+方向分别迭代,并计算对应的残差rK0-和rK0+,迭代方向为残差减小的较快的方向,如果rK0-减小的较快,则s=-1,否则s=1。

步骤 7从u中取出最大的L个值对应的索引存入索引集Fn中,并更新候选集Cn=Tn-1∪Fn。


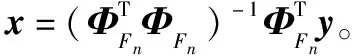
SAGI算法虽然较SAMP算法在重构效果方面有明显提升,但由于在预测稀疏度和确定迭代方向时步长取值均为1,导致算法迭代次数并没有明显的减少,所以算法运行时间只是小幅度减少。针对该问题,本文提出了一种基于RIP的稀疏度预测方法,该方法可以快速精确地逼近信号的真实稀疏度,同时为了在SAGI算法的基础上进一步提升算法的重构性能,本文算法对观测矩阵采取了优化。
3 RSAMP算法
3.1 基于RIP的稀疏度预测
由于文献[17]中提出的SAGI算法预测的稀疏度存在欠估计问题,因此在完成稀疏度预测后需要确定迭代方向,再利用自适应的方式完成信号的估计。为了更快更准确地预测稀疏度,本文给出了稀疏度过估计的判据。
假定观测矩阵Φ满足RIP准则[21],即如果存在一个常数δk∈(0,1),使得对于任意信号x(稀疏度为K),都满足:

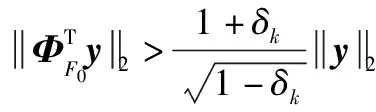
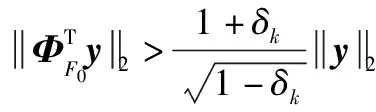
取相关系数u中前K个最大元素的索引得到集合F0。
由于
(4)
则根据RIP准则,有
(5)
(6)
式(5)和式(6)相乘得
(7)
根据矩阵范数的不等式关系可知
(8)
进一步整理得
(9)
由此可得
F0⊇F
(10)
这与K0≤K是矛盾的,因此判据成立。
证毕


3.2 观测矩阵的优化处理
SAMP算法和SAGI算法均采用高斯矩阵、伯努利矩阵等随机矩阵作为观测矩阵,其中观测矩阵原子间的相干性会影响其与残差的匹配,而观测矩阵与残差的匹配是否精确会影响算法整体重构性能。由CS理论可知,观测矩阵原子间的相干性越低,观测矩阵与残差的匹配越准确[23]。通过研究发现主成分分析方法可以通过线性变换的方式将一组相干变量转化成一组不相干变量。因此,本文利用主成分分析的思想对观测矩阵进行优化,减弱其原子之间的相干性,以进一步提高算法的重构性能。其中相干性表示为
在满足RIP性质的前提下对观测矩阵进行如下处理:
设矩阵P为正交矩阵,通过观测矩阵Φ的正交变换获得矩阵C,即
C=PΦ
(11)
假设矩阵C满足μ(C)<μ(Φ),用C观测原始信号x,得
w=Cx
(12)
即w=Cx等价于y=Φx。
整理得
x=CTw=(PΦ)Tw=
(PΦ)TPy=(ΦTPTP)y=(PTPΦ)Ty
(13)
进一步整理得
y=(PTPΦ)x
(14)
令Z=PTPΦ,当PTP=(ΦΦT)-1时,
Z=(ΦΦT)-1Φ
(15)
综上,通过上述线性变换将矩阵Φ转换为低相干性矩阵Z。
3.3 算法实现
本文提出的RSAMP算法的具体实现步骤如下。
步骤 1输入观测矩阵Φ,测量向量y,观测数M。

步骤 3i=i+1,Ki=round[(Kmin+Kmax)/2]。
步骤 4对观测矩阵Φ做优化处理,得观测矩阵Z。
步骤 5通过公式u=|〈Z,r〉|计算相关系数,并从u中取出最大的Ki个值对应的索引加入索引集F0。
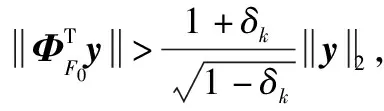
步骤 7在K-和K+方向分别迭代,并计算对应的残差rK-和rK+,迭代方向为残差减小的更快的方向,如果rK-减小的更快,则s=-1,否则s=1。

步骤 9从u中取出最大的K个值对应的索引加入索引集Fn中,并更新候选集Cn=Tn-1∪Fn。



4 仿真实验和分析
为了验证RSAMP算法的重构性能,本文在Matlab R2016仿真环境下进行了实验。主要验证基于RIP的稀疏度预测方法的有效性、观测矩阵优化后的低相干性和RSAMP算法信道估计性能的优越性。其中SAMP算法的运行时间和重构精度会因步长s取值的不同而产生差异,本文考虑到时间和精度的折中问题,通过实验和分析将SAMP算法的步长s取值为5。
4.1 基于RIP的稀疏度预测方法的验证
仿真1主要验证本文提出的基于RIP的稀疏度预测方法的可行性,并对比RSAMP与SAMP、SAGI算法的单次运行时间。仿真选取的实验信号为一维随机信号,其中信号长度N=256,观测数M=128,信号稀疏度K的预测范围为[5,32],在其他参数不变的情况下,令稀疏度K从5变化至32,比较预测稀疏度与真实稀疏度。为避免随机因素对实验结果造成影响,仿真1涉及的数据均是运行100次后求得的平均。
通过图1可以明显看出,RSAMP算法预测的稀疏度与真实的稀疏度之间的差异非常小,由此可证明基于RIP的稀疏度预测方法是有效的。SAGI算法在稀疏度预测阶段由于步长取值为1,所以需要进行多次迭代,加之其预测的稀疏度与真实稀疏度之间的差值较大,在确定迭代方向之后同样需要迭代多次。而基于RIP的稀疏度预测方法由于动态的增大了步长,所以在信号观测数M=128时,最多迭代5次即可完成预测。此外RSAMP算法预测的稀疏度与真实的稀疏度之间的差值仅为1,所以在确定迭代方向之后仅需迭代一次即可,进一步减少了算法运行的时间。
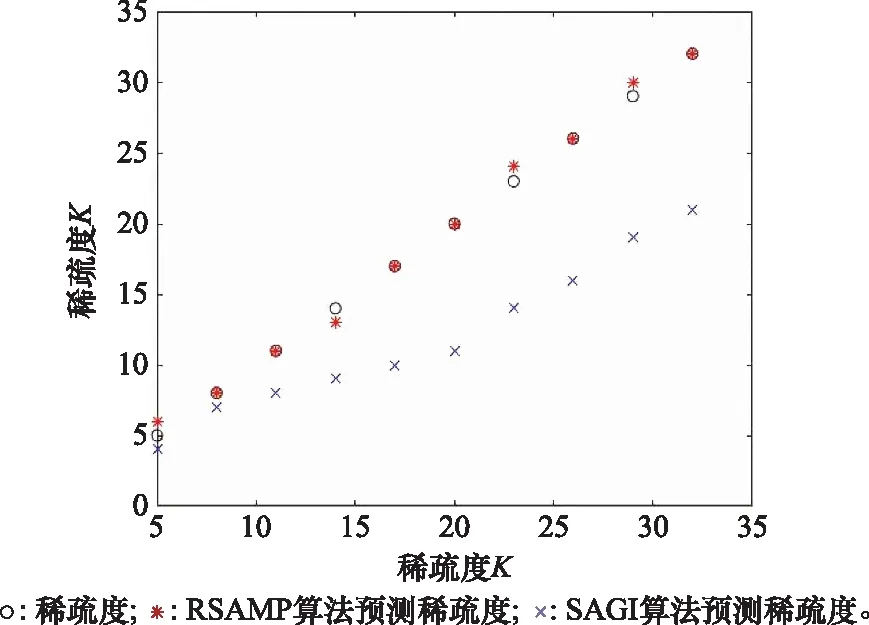
图1 算法预测稀疏度与真实稀疏度间的对比

表1 不同算法的单次运行时间
4.2 观测矩阵低相干性的验证
仿真2主要验证本文优化处理得到的观测矩阵Z的低相干性,并对比了不同观测数下相干性比值的改变。仿真选取的实验信号为一维随机信号,其中信号长度N=256,稀疏度K=10,信号观测数M的取值范围为[40,210],在其他参数不变的情况下,令观测数M从40变化至210,观察相干性比值的变化。为避免随机因素对实验结果造成影响,仿真2涉及的数据均是运行100次后求得的平均值。
仿真2采用相干性比值来衡量矩阵Z的低相干性。本文相干性比值的定义为
(16)
通过图2可得知相干性比值μ>1,即μ(Z)<μ(Φ),由此可以说明优化处理后获得的矩阵Z的相干性低于矩阵Φ的相干性,而且随着观测数M的增大,矩阵Z的低相干性更加明显。
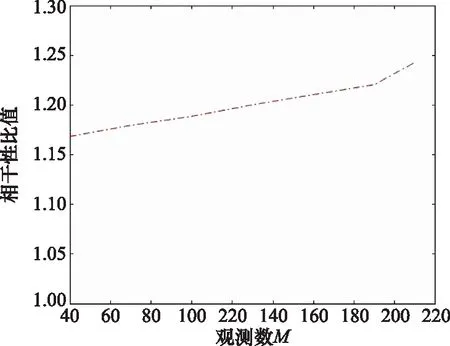
图2 不同观测数下相干比值的变化
4.3 基于RSAMP算法信道估计性能验证
仿真3主要验证本文提出的RSAMP算法的信道估计性能,将其与SAMP、SAGI算法进行对比,同时为了检验优化观测矩阵的有效性,在仿真3中也对比了未优化观测矩阵的RSAMP算法(简称为URSAMP)。在OFDM系统中,采用16QAM映射方式,信道长度L=100,子载波数N=512,非零抽头个数为6,系统参数在一个OFDM符号周期内不发生改变。为避免随机因素对实验结果造成影响,仿真3涉及的数据均是运行1 000次后求得的平均值。具体系统仿真设置参数如表2所示。

表2 系统仿真参数
仿真3采用均方误差(mean square error, MSE)、误码率(bit error rate, BER)和运行时间来衡量算法信道估计的性能[24]。
(1)MSE性能分析
本文MSE的定义为
(17)

对于OFDM系统而言, MSE值越小,信道估计误差就越小。信噪比越小表示信号受到的干扰越大,当信噪比相同时,算法的MSE值越小表示算法的抗干扰能力越好。通过图3可以明显看到,随着信噪比的增大,SAMP、SAGI、RSAMP算法的MSE值均开始减小,但本文提出的RSAMP算法相比其他两种算法具有更小的MSE值,而且随着信噪比的增大优势更加明显。

图3 不同信噪比下MSE性能对比
(2)BER性能分析
对于OFDM系统而言,BER值越低,信道估计就越准确。在信噪比较小时,信道受到噪声的影响较大,导致各算法BER值间的差异较小。通过图4可以明显看到,随着信噪比的增大,噪声的影响逐步减弱,SAMP、SAGI、RSAMP算法的BER值均开始减小,但本文提出的RSAMP算法相比其他两种算法具有更小的BER值,而且随着信噪比的增大优势更加明显。

图4 不同信噪比下BER性能对比
通过图3和图4可以看出RSAMP算法的MSE值、BER值均低于URSAMP算法,即优化观测矩阵提高了算法的信道估计性能,验证了优化处理的有效性。URSAMP算法相较于SAGI算法而言,因具有更精确的支撑集和初始残差,所以信道估计性能略优于SAGI算法。
(3)运行时间分析
对于实际的应用而言,算法信道估计的运行时间也是需要重点考虑的因素。在同等条件下, SAMP、SAGI、RSAMP算法信道估计的运行时间如图5所示。
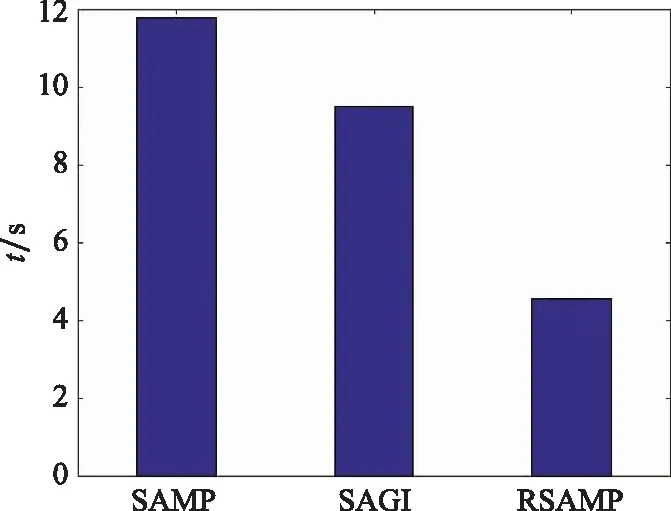
图5 算法信道估计的运行时间
通过图5可以看出,SAMP、SAGI、RSAMP信道估计的运行时间分别为11.771 5 s、9.515 2 s、4.550 9 s。本文提出的RSAMP算法由于改进了稀疏度预测方法,因此在时间方面具有明显的优势。
5 结 论
本文研究了OFDM系统稀疏信道估计问题,针对SAGI算法在时间和性能方面存在的不足,提出了RSAMP算法,该算法通过提出一种基于RIP的稀疏度预测方法以及观测矩阵的优化处理,不仅缩短了算法的运行时间,还提高了算法的重构性能。此外,本文从MSE、BER和时间方面对比了RSAMP算法与SAMP、SAGI算法信道估计的性能,仿真结果显示,在相同条件下,RSAMP算法较SAMP、SAGI算法具有更低的MSE值、BER值和运行时间。

