BL-代数的直觉模糊滤子度
彭家寅
(内江师范学院数学与信息科学学院, 四川 内江 641100)
1 引言
模糊集[1]是机器学习和控制论的重要基础理论, 为模糊逻辑推理提供了理论基础.比如, 文献[2] 研究了正、负模糊规则系统、极端机器学习和图像分类. 文献[3] 提出了一种基于模糊熵的边缘信息提取的分层多级阈值方法, 等等. 自文献[4] 引入了模糊子群的概念以来, 各种代数结构已被模糊化, 而且模糊代数在诸如数据分析、模糊控制、模糊识别、智能决策支持系统、专家系统等不确定信息处理中有广泛的应用[5-9].
文献[5] 为了用代数方法研究多值逻辑引入了BL- 代数, 其动机之一是给本逻辑提供对应的代数结构, BL- 代数体现了诸如ukasiewicz 逻辑、G˝odel 逻辑以及乘积逻辑等一些最重要的多值逻辑的共性; 另一个动机是为研究[0,1] 上连续t- 模提供一种代数方法. 滤子理论在逻辑代数的研究中起着重要的作用, 从不确定信息的角度看, 相应推理系统中的可证明公式集可以用这些代数语义的模糊滤子来描述[10]. 许多学者对BL-代数的滤子做了大量的研究[11-18], 特别是文献[18] 将文献[19] 提出的直觉模糊集应用于BL- 代数中, 建立了BL- 代数的直觉模糊滤子理论, 研究几种直觉模糊滤子的性质和它们之间的一些关系.
文献[20] 为研究一个模糊子集满足模糊子群条件的程度, 引入了模糊子群度的概念, 讨论了它的基本性质及其等价刻画. 文献[21] 借助一般t- 模对模糊子群度进行了重新定义, 研究其性质或相关关系. 此后, 一些学者对不同模糊代数系统进行了度量化研究, 获得一系列优秀成果[22-26].
本文将上述模糊代数系统度量化的思想推广到直觉模糊代数系统的情形, 引入BL-代数的直觉模糊滤子度的概念, 研究其性质、刻画和相关关系, 为其它直觉模糊系统的度量化提供参考与借鉴.
2 预备
定义2.1[11]一个(2,2,2,2,0,0) 型代数结构(L,∧,∨,⊗,→,0,1) 叫做BL- 代数,如果它满足下列条件:
(1) (L,∧,∨,0,1) 为一个有界格, 0 和1 分别是最小与最大元;
(2) (L,⊗,1) 为一个阿贝尔幺半群, 即⊗是交换、结合的, 且x ⊗1 =x对任意x ∈L都成立;
(3)⊗和→为伴随对, 即x ⊗y ≤z当且仅当x ≤y →z对任意x,y,z ∈L都成立;
(4)x ∧y=x ⊗(x →y) 且(x →y)∨(y →x)=1.
定义2.2[11]称BL- 代数L的子集F为L的一个滤子, 如果1∈F且对任意x,y ∈F, 若x ∈F,x →y ∈F, 那么y ∈F.
记BL- 代数L的全体滤子构成的集合为F(L). 设L和L′是两个BL- 代数, 若映射f:L →L′满足对任意x,y ∈L, 且∗∈{∧,∨,⊗,→}都有f(x ∗y)=f(x)∗f(y), 则称f为从BL- 代数L到BL- 代数L′上的同态映射. 特别地, 当f为双射时, 称之为同构映射.

定义2.3[19]设U为非空论域集, 称A为U上的一个直觉模糊子集, 如果

其中, 模糊集µA:x →[0,1] 和模糊集νA:x →[0,1] 满足: 对任意x ∈U, 都有0≤µA(x)+νA(x)≤1. 分别称µA(x) 和νA(x) 为元素x ∈U的隶属度与非隶属度.
对于[0,1] 上的任意两个实数a和b, 记a ∧b=min{a,b},a ∨b=max{a,b}. 设A和B都是U上的直觉模糊集,规定: 对任意x ∈U, ˜α=(λ1,λ2)∈[0,1]2且λ1+λ2≤1,有

设f:L →L′是从BL- 代数L到BL- 代数L′上的映射,A和B分别是BL-代数L和BL- 代数L′上的直觉模糊集,A的象f(A) 和B的原象f−1(B) 分别定义为∀x ∈L,∀y ∈L′, 有
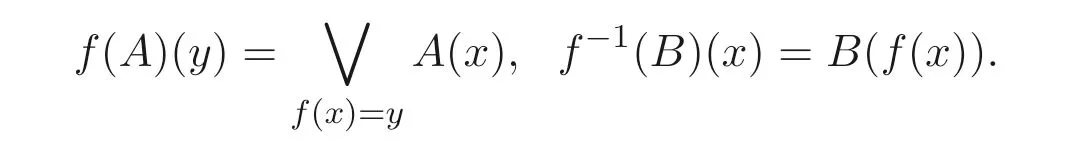
记D={(a,b)∈[0,1]2|a+b ≤1}, 则由文献[3] 知D为[0,1]2的完备子格, 这里[0,1]2中的序≤由下式确定: (a1,a2)≤(b1,b2)⇔a1≤b1,a2≥b2. 容易知道, [0,1]2中最小元与最大元分别为˜0=(0,1) 和˜1=(1,0).
将文献[27] 中模糊蕴涵算子的定义推广到直觉模糊逻辑中, 有
定义2.4设映射˜I:D×D →D, 若˜I关于第一变量不增, 关于第二变量不减, 并满足˜I(˜1,˜0)=˜0 且˜I(˜0,˜0)= ˜I(˜1,˜1)=˜1, 则称˜I为一个直觉模糊蕴涵.
例如, 对任意˜α,˜β ∈D, 定义˜I(˜α,˜β)=∨{˜t ∈D| ˜α ∧˜t ≤˜β}, 则˜I为一个直觉模糊蕴涵, 并称它为˜R- 直觉蕴涵, 通常记为˜α˜→˜β. 容易证明˜R- 直觉蕴涵具有如下性质:
引理2.1设I为指标集, ˜α,˜β,˜αi,˜βi ∈D(i ∈I), 则

(2) 若˜α1≤˜α2, 则˜α1˜→˜β ≥˜α2˜→˜β;(3) 若˜β1≤˜β2, 则˜α˜→˜β1≤˜α˜→˜β2.
定义2.5[18]设L是BL- 代数, 称L上的一个直觉模糊集A为L的一个直觉模糊滤子, 如果它满足: 对任意x,y ∈L, 有
(1)A(1)≥A(x);
(2)A(y)≥A(x)∧A(x →y).
注2.1定义2.5 的条件(1) 等价于µA(1)≥µA(x) 且νA(1)≤νA(x); 条件(2) 等价于µA(y)≥µA(x)∧µA(x →y) 且νA(y)≤νA(x)∨νA(x →y).
3 直觉模糊滤子度
定义3.1设A是BL- 代数L上的一个直觉模糊子集, 令

则称mL(A) 为BL- 代数L的直觉模糊滤子度.
注3.1记mL(A)=(ml(µA),mr(νA)), 则

mL(A)是用来刻画BL-代数的一个直觉模糊子集A是否是BL-代数的直觉模糊滤子的程度.具体地,ml(µA)表示直觉模糊子集A为BL-代数的直觉模糊滤子的程度,mr(νA)表示直觉模糊子集A不是BL- 代数的直觉模糊滤子的程度, 而1−ml(µA)−mr(νA)则表示直觉模糊子集A为BL- 代数的直觉模糊滤子的犹豫程度. 显然, 当A是模糊子集时,ml(µA)=m(A),mr(νA)=1−m(A), 这里m(A) 为类似文献[26] 所定义的模糊滤子度, 这表明直觉模糊滤子度是模糊滤子度的推广, 前者更加细腻地刻画了模糊代数子系统保持模糊代数系统的程度.
例3.1设L={0,a,b,1},⊗和→的定义分别见表1 和表2, 这里0 表1 ⊗的运算表 表2 →的运算表 定理3.1设A是BL- 代数L的直觉模糊子集, 则A为L的直觉模糊滤子的充分必要条件是mL(A)=(1,0). 证明令 假设A为BL- 代数L的直觉模糊滤子, 则由定义2.5 及注2.1 可知, 对任意x,y ∈L,有 由ε的任意性知,µA(x)≤µA(1). 同理, 由∨C(x,y)=1 可得 由定义2.5 知,A是BL- 代数的直觉模糊滤子. 例3.2设L是例3.1 中所示的BL- 代数, 定义L上的直觉模糊子集A如下: 容易验证A是BL- 代数L的直觉模糊滤子, 通过计算也有mL(A)=(1,0). 注3.2在例3.1 中定义的直觉模糊子集A的度为mL(A) = (0.4,0), 依定理3.1知A不是直觉模糊滤子. 另一方面, 由µA(b) = 0.5> 0.4 =µA(1) 知,A不满足定义2.5(1), 这也表明A不是L的直觉模糊滤子. 为了给出直觉模糊滤子度的等价刻画, 先考虑如下引理. 引理3.1设A是BL- 代数L的直觉模糊子集, 则对于(a,b)∈D,mL(A)≥(a,b)的充分必要条件是∀x,y ∈L, 都有 证明令 定理3.2设A是BL- 代数L的直觉模糊子集,mL(A)=(ml(µA),mr(νA)), 则 证明设mL(A)=(c,c′), 由引理3.1 知,∀x,y ∈L, 有∀x,y ∈L, 都有 记h=∨{a ∈[0,1]|∀x,y ∈L,µA(x)∧a ≤µA(1),µA(x)∧µA(x →y)∧a ≤µA(y)},则h ≥c. 下证h ≤c. 事实上,∀ε>0,∃tε ≥0, 使得tε>h −ε, 且 所以 由ε的任意性知,µA(x)∧h ≤µA(1),µA(x)∧µA(x →y)∧h ≤µA(y). 由引理3.1 得,c ≥h, 故c=h. 令h′=∧{b ∈[0,1]|∀x,y ∈L,νA(x)∨b ≥νA(1),νA(x)∨νA(x →y)∨b ≥νA(y)},则h′≤c′. 下证h′≥c′. 事实上,∀ε>0,∃sε ≤1, 使得sε 于是, 由ε的任意性有,νA(x)∨h′≥νA(1),νA(x)∨νA(x →y)∨h′≥νA(y). 依引理3.1 知,c′≤h′, 故c′=h′. 总上所述,mL(A)=(h,h′), 故结论成立. 注3.3定理3.2 的结论可以简单地表达如下: 定理3.3设A是BL- 代数L的直觉模糊子集,mL(A)=(ml(µA),mr(νA)), 则 证明为了讨论方便, 令 情形1: 证明B= (B1)(B2). 事实上, 对于任意a ∈B, 则∀x,y ∈L,都有µA(x)∧a ≤µA(1),µA(x)∧µA(x →y)∧a ≤µA(y), 所以a ∈B1∩B2, 于是a ≤∨B1,a ≤∨B2, 故a ≤(∨B1)∧(∨B2), 进而∨B ≤(∨B1)∧(∨B2). 由ε的任意性知, 由引理3.1 得,ml(µA)≥即∨B ≥(∨B1)∧(∨B2). 综上所述,∨B=(∨B1)∧(∨B2). 情形2: 证明∧B′=(∧B′1)∨(∧B′2):∀b ∈B′, 则∀x,y ∈L, 都有 由ε的任意性知,∀x,y ∈L,νA(x)∨≥νA(1),νA(x)∨νA(x →y)∨≥νA(y). 由引理3.1 知,mr(νA)≤即∧B′≤(∧B′1)∨(∧B′2). 总之, ∧B′=(∧B′1)∨(∧B′2). 为了利用直觉模糊子集的截集和强截集来刻画直觉模糊滤子度, 先给出如下引理. 引理3.2设A是BL- 代数L的直觉模糊子集,mL(A) = ˜α> ˜0, 则∀˜β ∈(˜0,˜α],A[˜β] =∅或A[˜β]是L的滤子. 证明记˜α=(λ1,λ2),˜β=(a1,a2), 则0 设x,x →y ∈A[˜β], 则 因mL(A)= ˜α, 依引理3.1 知, 所以1∈A[˜β]且y ∈A[˜β]. 由定义2.2 知,A[˜β]是BL- 代数L的滤子. 定理3.4设A是BL- 代数L的直觉模糊子集, 则 证明令mL(A) = ˜γ,B={˜α ∈D −{˜0}|∀˜β ∈(˜0,˜α],∅̸=A[˜β]∈F(L)}. 由引理3.2 知, ˜γ ∈B, 所以˜γ ≤∨B. 下面分两种情况来证明mL(A)≥∨B. (1)∀˜α=(a1,a2)∈B,∀x ∈L, 有 若不然,∃x0∈L,使得µA(x0)∧a1>µA(1)或νA(x0)∨a2<νA(1). 取b1=µA(x0)∧a1,b2=νA(x0)∨a2, 则 故˜β=(b1,b2)∈(˜0,˜α],x0∈A[˜β], 即x0∈A[˜β]且µA(1) 另一方面,依引理3.2 知,当˜β ∈(˜0,˜α]时,A[˜β]是BL-代数L的滤子,所以1∈A[˜β],从而µA(1)≥b1且νA(1)≤b2, 这与µA(1) 同理可证: (2)∀˜α=(a1,a2)∈B,∀x,y ∈L, 有 结合(1) 和(2), 由引理3.1 可得,mL(A)≥˜α. 由˜α在B中具有任意性, 所以mL(A)≥∨B. 综上所述,mL(A)=∨B, 故结论正确. 引理3.3设A是BL- 代数L的直觉模糊子集,mL(A) = ˜α> ˜0, 则∀˜β ∈[˜0,˜α),A(˜β)=∅或A(˜β)是L的滤子. 证明记˜α=(λ1,λ2),˜β=(a1,a2), 则0≤a1≤λ1且1≥a2≥λ2. 设x,x →y ∈A(˜β), 则 又mL(A)= ˜α, 依引理3.1 知,∀x,y ∈L, 有 所以µA(1)≥µA(x)∧λ1>a1. 同理,µA(y)>a1,νA(1) 定理3.5设A是BL- 代数L的直觉模糊子集, 则 证明令mL(A) = ˜γ,B={˜α ∈D −{˜0}|∀˜β ∈[˜0,˜α),∅̸=A(˜β)∈F(L)}. 由引理3.3 知, ˜γ ∈B, 所以˜γ ≤∨B. 下面证明mL(A)≥∨B. (1)∀˜α=(a1,a2)∈B,∀x ∈L, 有 另一方面, 依引理3.3 知, 当 ˜β ∈[˜0,˜α) 时,A(˜β)是BL- 代数L的滤子, 所以1∈A(˜β), 矛盾, 故(1) 为真. 同理可证: (2)∀˜α=(a1,a2)∈B,∀x,y ∈L, 有 结合(1) 和(2), 由引理3.1 可得,mL(A)≥˜α. 由˜α在B中具有任意性, 所以mL(A)≥∨B. 综上所述,mL(A)=∨B, 故结论正确. 以下讨论直觉模糊子集运算的直觉模糊滤子度的性质, 这里的运算是指“交”, “直积”, “同态” 或“同构”. 定理4.1设Ai为BL- 代数L上的直觉模糊子集(i ∈I,I为任意指标集), 则 证明与定理4.1 的证明类似, 从略. 定理4.3设f:L →L′是BL- 代数L到BL- 代数L′上的同态映射,A′为BL-代数L′上的直觉模糊子集, 则 证明由定义3.1 及f:L →L′为同态映射可知 即,mL′(A′)≤mL(f−(A′)), 故结论成立. 注4.1定理4.3 中的映射f:L →L′是同构映射时,则有mL′(A′)=mL(f−(A′)). 定理4.4设f:L →L′是BL- 代数L到BL- 代数L′上的同构映射,A为BL-代数L上的直觉模糊子集,mL(A)>˜0, 则mL(A)=mL′(f(A)). 证明由定理3.2 可知 注意到f:L →L′是同构映射, 对∀x′,y′′∈L′及1′∈L′, 分别存在唯一的x,y,i ∈L,使得f(x)=x′,f(y)=y′,f(1)=1′,且f(x →y)=f(x)→′f(y)=x′→′y′, 故



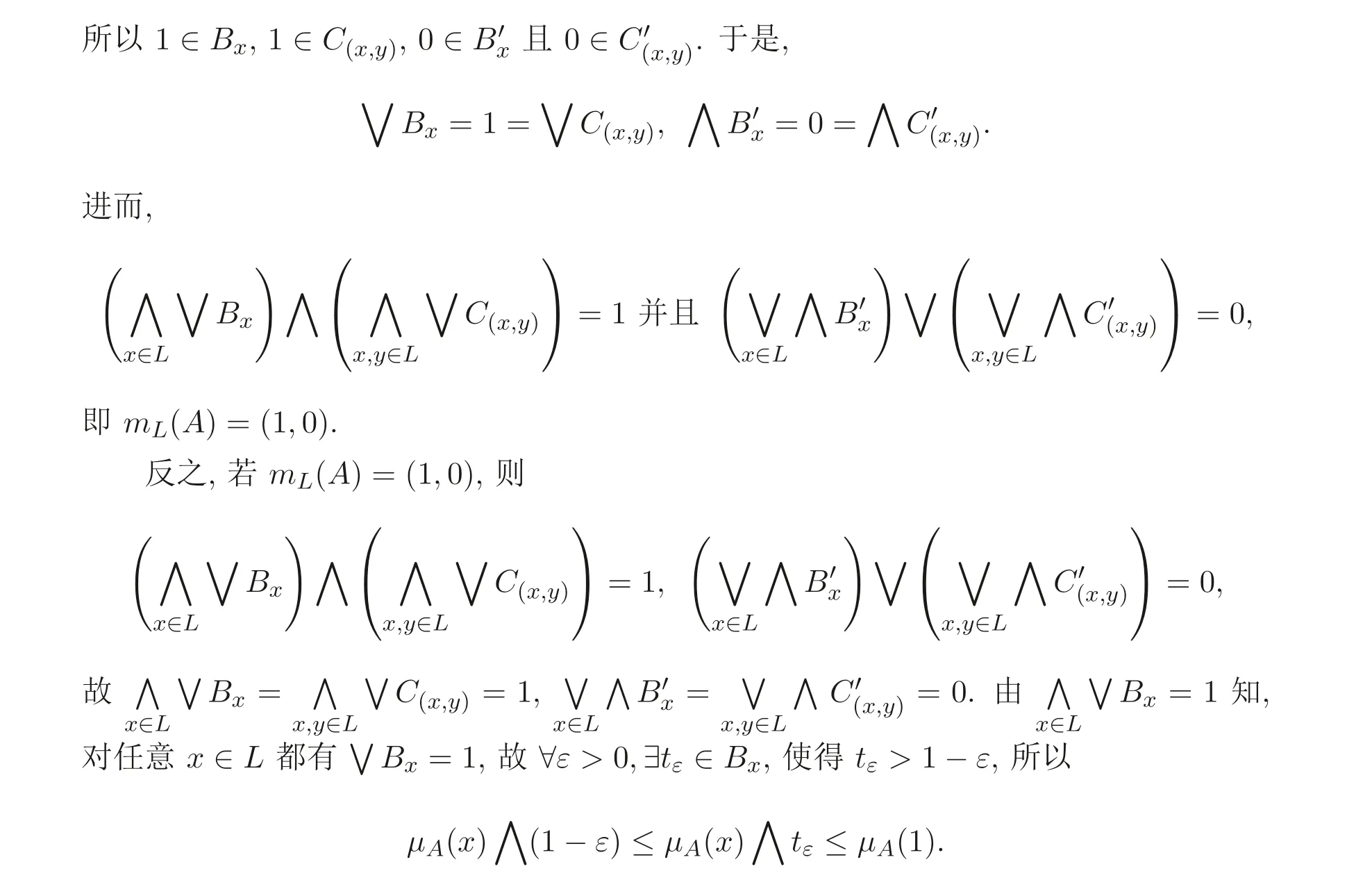








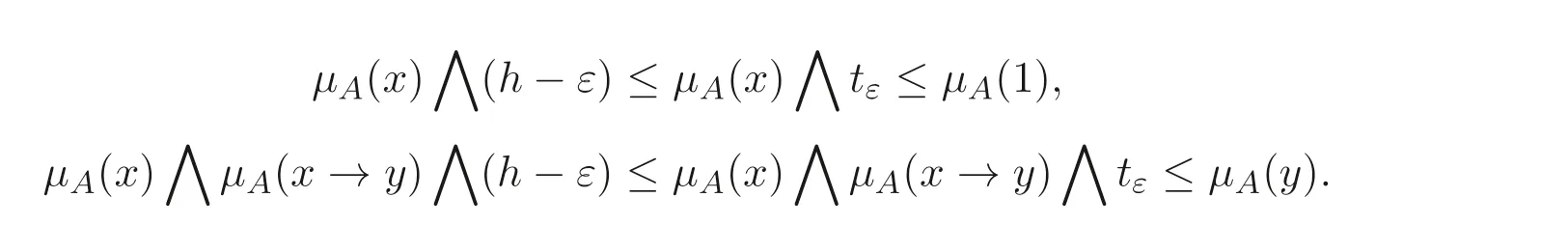


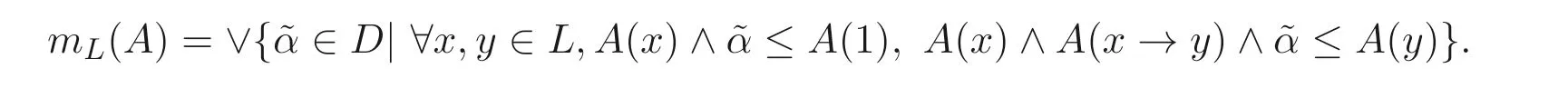

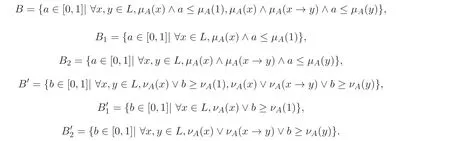



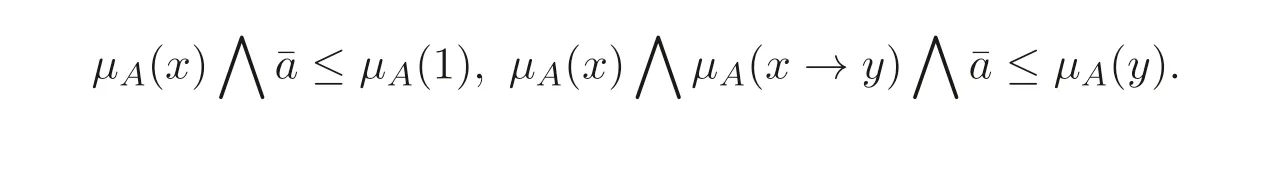





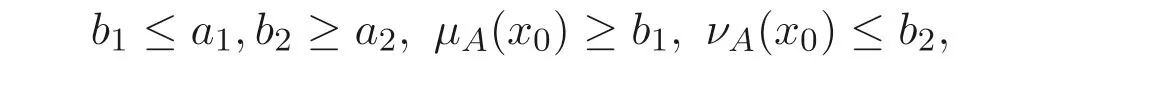

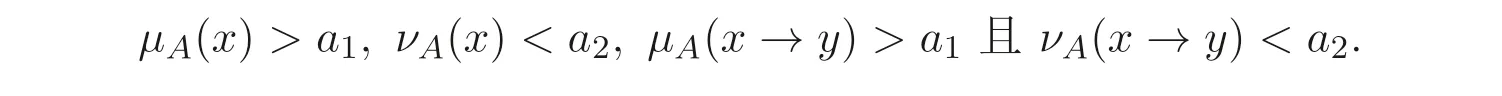
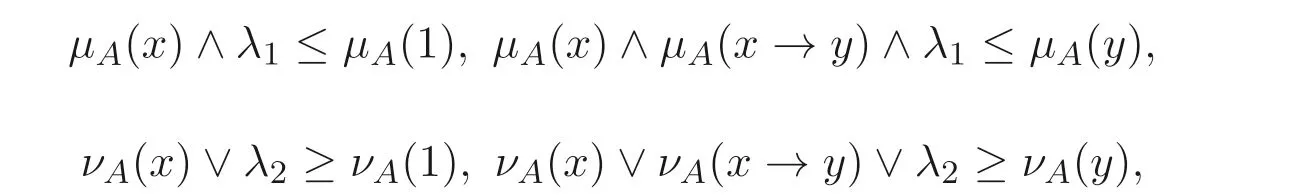




4 直觉模糊滤子度的性质







