基于热重分析法的苯基硅橡胶热分解行为研究

王雪蓉，王倩倩，刘运传，周燕萍，姚 凯，马衍东

（山东非金属材料研究所，山东 济南 250031）

苯基硅橡胶是甲基乙烯基苯基硅橡胶的简称，指主链中含有苯基硅氧烷或甲基苯基硅氧烷链节的高相对分子质量线型聚硅氧烷，其与填料、有机过氧化物硫化剂、加工助剂等混合后，经硫化制成弹性体。苯基硅橡胶除具备甲基乙烯基硅橡胶的压缩永久变形小、使用温度范围宽、耐老化及电气性能好外，还具有优良的耐高低温、减震、耐烧蚀和耐辐照等性能。目前苯基硅橡胶制品已广泛应用于航空航天和电子电器等领域。

近年来，研究人员在苯基硅橡胶的制备、改性及其应用拓展等方面研究较多[1-7]，有研究人员通过热分析对苯基硅橡胶和甲基乙烯基硅橡胶的耐高温性能进行对比，发现甲基苯基硅氧烷链节的引入可提高苯基硅橡胶的热分解温度并降低特定温度下热质量损失率，使其耐高温性能有所提升，此外还有研究人员探讨了金属氧化物、硫化剂、填料等对苯基硅橡胶耐高温性能的影响，但对于苯基硅橡胶的热分解过程及其机理研究较少。热分析方法已广泛用于橡胶材料热分解反应研究[8-14]。

本工作运用热重分析（TGA）技术，对苯基硅橡胶在空气气氛下的热分解行为及其规律进行研究，分别利用Flynn-Wall-Ozawa[15]，Kissinger，Friedman以及Coast-Redfern法等具有代表性的动力学方法得到了苯基硅橡胶的热分解表观活化能（Ea）等热分解动力学参数。

1 实验

1.1 主要原材料

苯基硅橡胶，苯基质量分数为0.25，中蓝晨光化工研究院有限公司提供。

1.2 试验仪器及条件

STA449C型同步热分析仪，德国耐驰公司产品。测试条件如下：温度范围 30～700 ℃，升温速率（β） 5，10，15，20 ℃·min-1，空气气氛，气体流量 50 mL·min-1，样品质量 约10 mg。

2 结果与讨论

2.1 苯基硅橡胶热分解过程分析

图1所示为苯基硅橡胶在空气气氛下的TGA和微商热重分析（DTG）曲线。

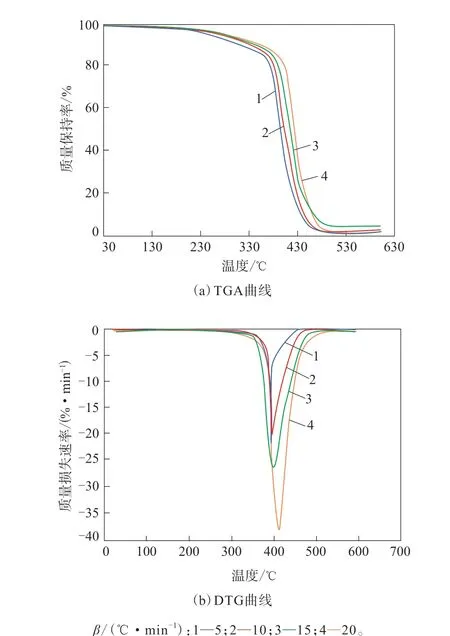
图1 苯基硅橡胶在空气气氛下的TGA和DTG曲线Fig.1 TGA and DTG curves of phenyl silicone rubber in air atmosphere

从图1可以看出，苯基硅橡胶热分解过程只有一个主要的质量损失平台，在200 ℃之前苯基硅橡胶基本不分解，200 ℃之后开始发生热分解，随着温度的升高，热分解速率逐渐增大，达到650 ℃时基本分解完全，发生的主要是分子链的热裂解，同时伴随发生碳的氧化反应。

苯基硅橡胶在空气气氛中不同β下的热分解特性参数见表1。

由表1可以看出，β由5 ℃·min-1提高至20℃·min-1，苯基硅橡胶的热分解起始温度由375.5℃升至402.9 ℃，质量损失率为5%时的热分解温度由262.6 ℃升至293.9 ℃，质量损失率为10%时的热分解温度由331.9 ℃升至368.0 ℃，最大热分解速率时的温度由390.5 ℃升至418.4 ℃。这说明苯基硅橡胶的热分解特性参数依赖于β，β越大，热分解温度越高。这主要是因为β较小时，热量传递的时间较为充足，样品内部热量分布较均匀，而随着β的增大，苯基硅橡胶分子结构中的链段松弛运动对温度滞后的现象越来越明显，表现为热质量损失温度向高温方向移动。

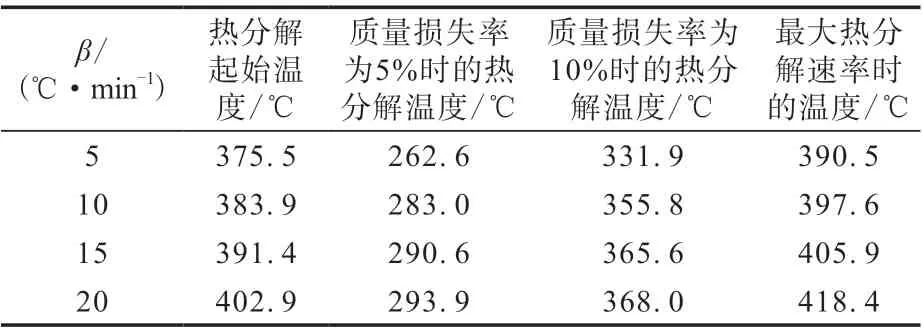
表1 苯基硅橡胶在空气中不同β下的热分解特性参数Tab.1 Thermal decomposition characteristic parameters of phenyl silicone rubber at different β in air

2.2 苯基硅橡胶热分解动力学分析

本工作采用Flynn-Wall-Ozawa和Friedman法对苯基硅橡胶的热分解动力学进行分析，这两种方法为多重扫描速率法，对采用不同β测得的TGA曲线进行分析，由于用到多条TGA曲线在同一转化率（α）处的温度数据，因此也称为等转化率法。此类方法能够在不涉及动力学反应机理函数的条件下获得可靠的Ea，避免了由于反应机理函数的假设不同造成的误差，还可通过比较不同α下Ea的数值来验证整个过程中反应机理的一致性。此外采用Kissinger法最大质量损失速率理论公式计算不同β下DTG曲线得到苯基硅橡胶在空气中的Ea，并结合以上3种方法对Coats-Redfern法的热分解反应函数进行判定。

2.2.1 Flynn-Wall-Ozawa法

Flynn-Wall-Ozawa法是利用一定的α下聚合物的Ea与α存在定量关系，通过不同β下聚合物的TGA曲线得到的不同α下的分解温度可计算Ea。Flynn-Wall-Ozawa法的方程如下：

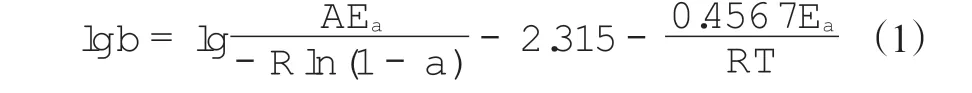
式中：A为指前因子，min-1；R为气体常数，8.314 J·（mol·K）-1；T为某一α对应的热分解温度，K。

在相同α下，lgβ与1/T成线性关系，以各个α下对应的lgβ对1/T进行线性拟合，由直线斜率即可计算出不同α下的Ea。本试验计算时α分别取10%，20%，30%，40%，50%，60%，70%，80%，90%，拟合得到9条直线，分别计算出苯基硅橡胶的Ea。

4个β下α为10%～90%的苯基硅橡胶热分解的Flynn-Wall-Ozawa拟合直线如图2所示。

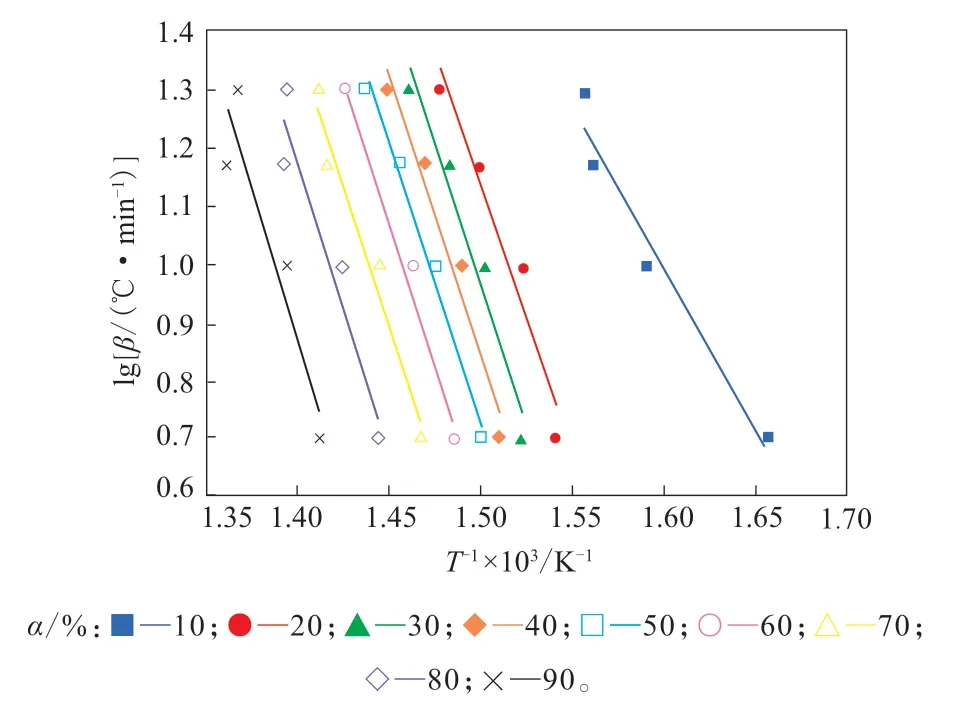
图2 不同α下苯基硅橡胶热分解的Flynn-Wall-Ozawa拟合直线Fig.2 Flynn-Wall-Ozawa fitting lines of thermal decomposition of phenyl silicone rubber at different α

从图2可以看出，各组数据点的线性相关性较好，拟合得到一组近似平行的直线。

根据各拟合直线的斜率计算得到的不同α下苯基硅橡胶的Ea见表2。

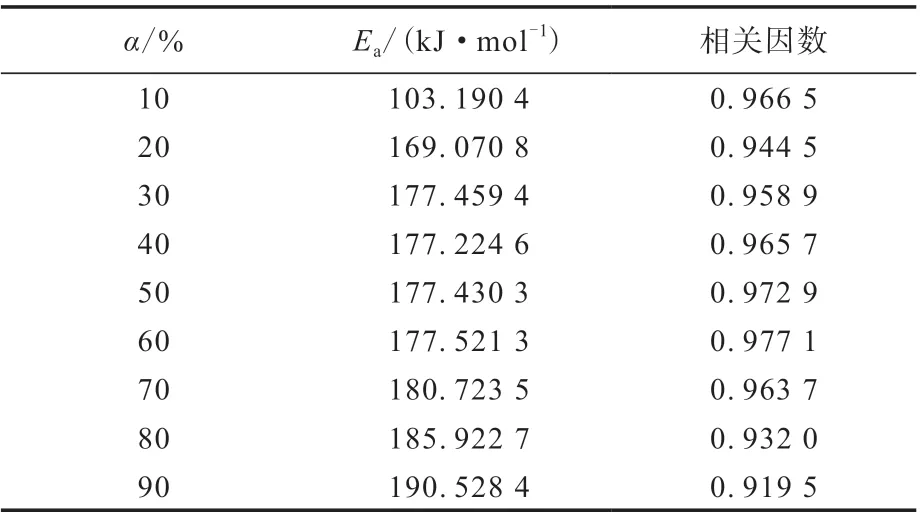
表2 不同α下Flynn-Wall-Ozawa法计算得到的苯基硅橡胶的EaTab.2 Ea of phenyl silicone rubber calculated by Flynn-Wall-Ozawa method at different α

不同α下苯基硅橡胶热分解的Ea变化曲线如图3所示。

由图3可以看出：苯基硅橡胶的Ea随α的增大总体呈增大趋势，整个过程可分为3个阶段，α为10%～30%时，Ea逐渐增大；α为30%～70%时，Ea趋于稳定；α为70%～90%时，Ea继续增大，稳定区域Ea基本一致，平均值为178.071 8 kJ·mol-1。

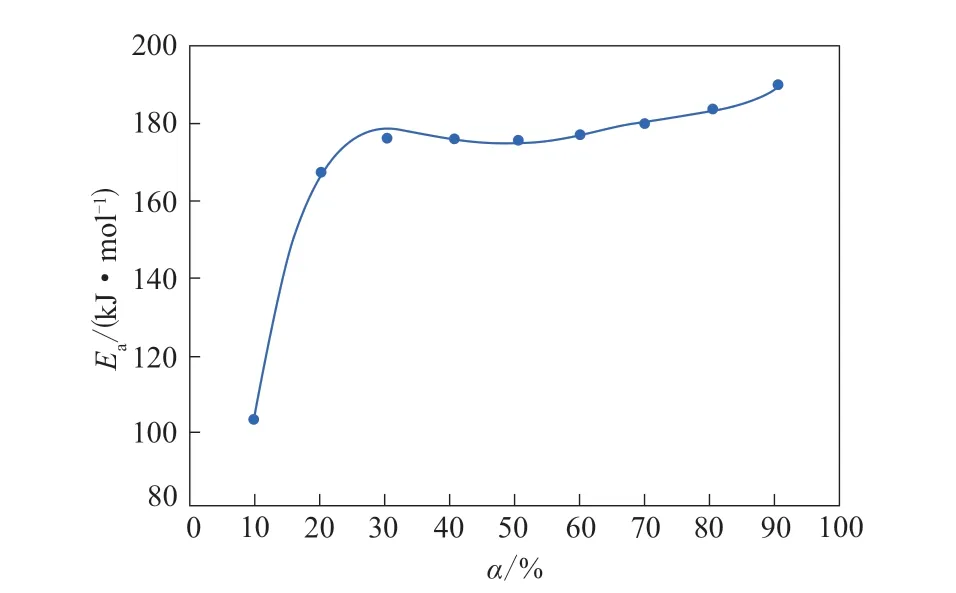
图3 不同α下Flynn-Wall-Ozawa法得到的苯基硅橡胶的Ea变化曲线Fig.3 Ea change curve of phenyl silicone rubber obtained by Flynn-Wall-Ozawa method at different α

2.2.2 Friedman法

Friedman法的计算公式为

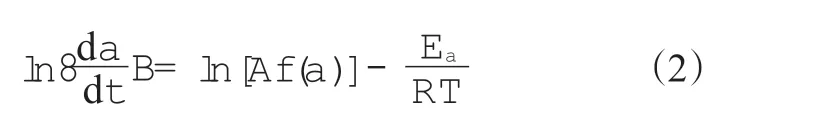
式中，dα/dt为反应的转化速率，f（α）为与α相关的反应机理函数，如果不同β下样品的热分解机理相同，则当α一定时，f（α）为恒定值。

以ln（dα/dt）对1/T作图，根据线性拟合后直线的斜率可求得不同α下的Ea。不同α下苯基硅橡胶热分解的Friedman拟合直线如图4所示。

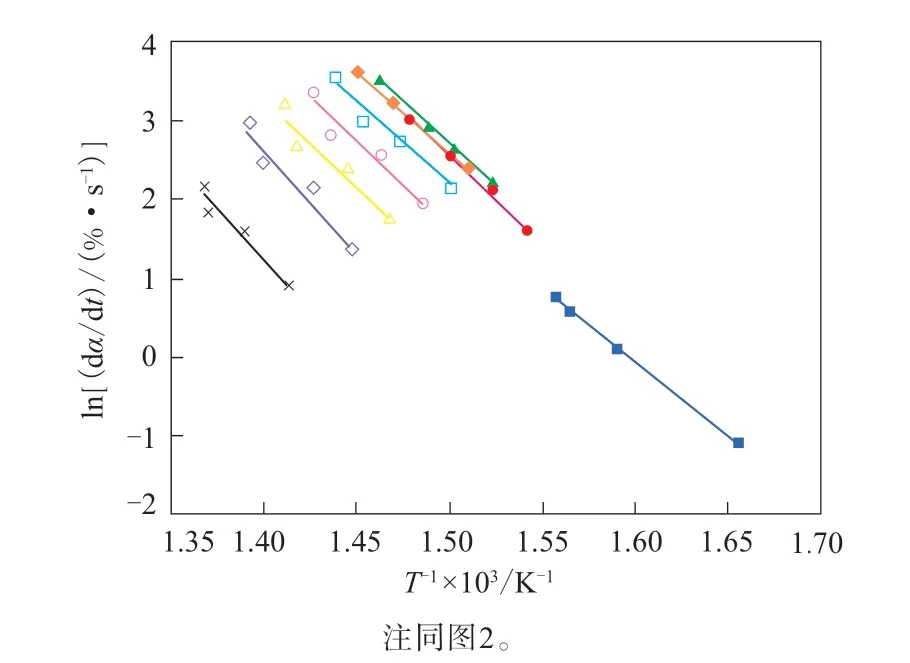
图4 不同α下苯基硅橡胶热分解的Friedman拟合直线Fig.4 Friedman fitting lines of thermal decomposition of phenyl silicone rubber at different α

由图4可见，在不同α下，ln（dα/dt）与1/T均呈良好的线性关系，说明不同β下苯基硅橡胶的热分解机理基本一致。

不同α下苯基硅橡胶的Ea计算结果见表3，Ea随α的变化趋势见图5。

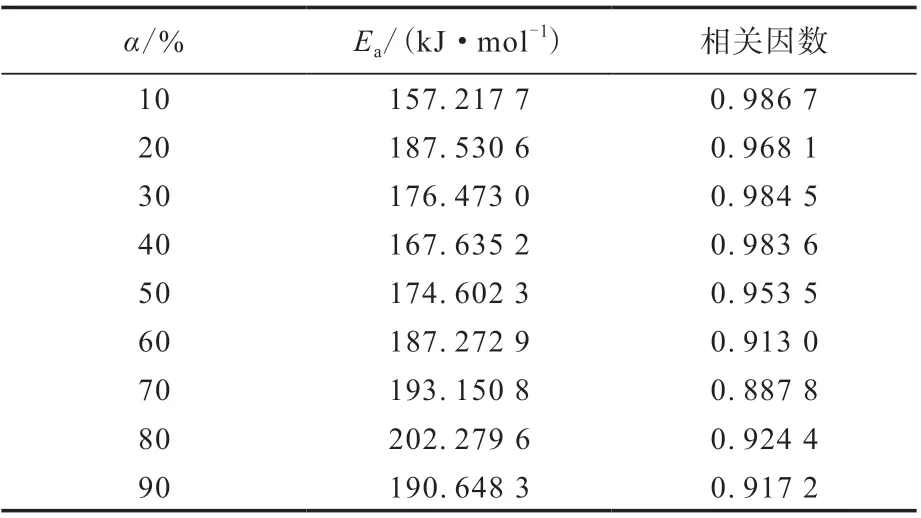
表3 不同α下Friedman法计算得到的苯基硅橡胶的EaTab.3 Ea of phenyl silicone rubber calculated by Friedman method at different α

在α为30%～70%的稳定区间内，由Friedman法计算得到的苯基硅橡胶的Ea平均值为179.826 8 kJ·mol-1，与Flynn-Wall-Ozawa法 的 计 算 结 果178.071 8 kJ·mol-1具有很好的一致性。这两种方法不需要设定反应机理函数而直接求解Ea，而且综合考虑了多种受热条件下的热分解规律，计算结果较为可靠。

2.2.3 Kissinger法

Kissinger法可以用来研究聚合物热分解反应，计算聚合物的Ea。Kissinger法是利用对多条DTG曲线的峰值温度（Tp）与β之间的关系进行求解，该方法计算简单，取点容易，适用于任何反应级数，但需要测出不同β下聚合物的DTG曲线。

Kissinger法的最大热质量损失理论公式为

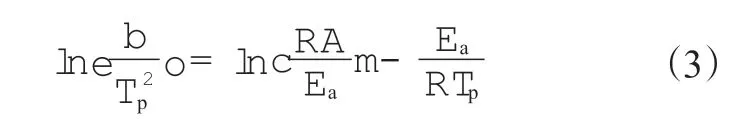
式中，Tp为DTG曲线的峰值温度，K。以ln（β/Tp2）对1/Tp作图，由拟合直线的斜率得到Ea。苯基硅橡胶热分解过程Kissinger法的热分解动力学计算结果示于表4，计算得到的Ea为182.633 kJ·mol-1。

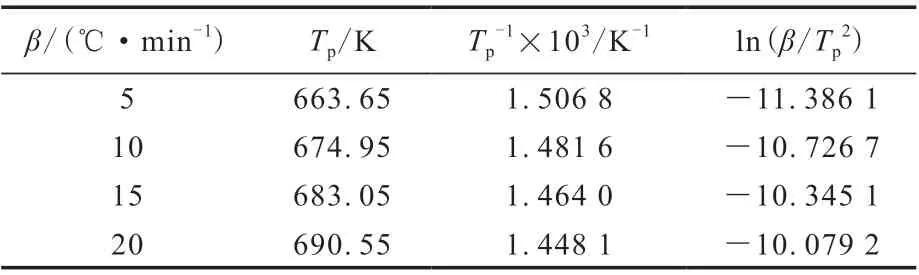
表4 苯基硅橡胶热分解过程Kissinger法的动力学计算结果Tab.4 Kinetic calculation results of Kissinger method during thermal decomposition of phenyl silicone rubber

苯基硅橡胶热分解的ln（β/T2p）-1/Tp拟合直线如图6所示，直线方程为y＝22.448x＋22.479，相关因数为0.991 1。

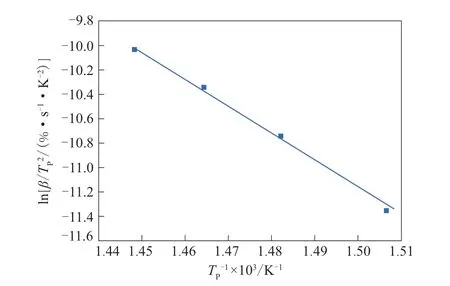
图6 苯基硅橡胶热分解的ln（β/Tp2）-1/Tp拟合直线Fig.6 ln（β/Tp2）-1/Tp fitting line of thermal decomposition of phenyl silicone rubber

2.2.4 Coats-Redfern法

由Flynn-Wall-Ozawa法和Friedman法的计算结果可知，除去反应初期和末期的不稳定性，α为30%～70%时，Ea基本保持稳定，这说明两种方法的苯基硅橡胶热分解反应机理基本一致。Coats-Redfern法方程为

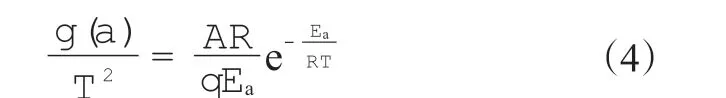
式中：g（α）为反应机理函数，为DTG曲线的峰值温度，K；q为常数。

如果反应机理函数g（α）正确，则ln[g（α）/T2]与1/T呈线性关系。选取多种常用的动力学反应机理函数g（α）代入Coats-Redfern方程[16]，以ln[g（α）/T2]对1/T作图，通过拟合直线的斜率计算出Ea。通过计算，结果显示代入以下14种反应机理函数后，苯基硅橡胶的ln[g（α）/T2]与1/T线性相关性较好（相关因数大于0.97）。表5所示为不同机理函数求解得到的苯基硅橡胶的Ea。

表5 Coats-Redfern法计算得到的苯基硅橡胶的EaTab.5 Ea of phenyl silicone rubber calculated by Coats-Redfern method

从表5可以看出，虽然代入多种反应机理函数均可计算得到Ea，但每种反应机理获得的苯基硅橡胶的Ea差别较大，范围为108.319～375.442 kJ·mol-1。因此仅通过拟合直线的线性相关性不足以得到准确可靠的动力学结果，还必须与其他计算方法结合进行验证。

将Coats-Redferm法获得的苯基硅橡胶的Ea与Friedman法、Flynn-Wall-Ozawa法 以 及Kissinger法获得的Ea进行对比。结果表明，反应机理函数为g（α）＝[（1＋α）－1/3－1]2时，苯基硅橡胶的Ea平均值为174.692 kJ·mol-1，标准偏差为15.916 kJ·mol-1，该Ea平均值与其他方法的计算结果最为相近，由此可以得出，g（α）＝[（1＋α）－1/3－1]2为苯基硅橡胶在空气气氛下最理想的Coats-Redferm法的热分解反应机理函数，反应机理为三维扩散控制。

3 结论

采用TGA法研究了苯基硅橡胶在空气气氛下的热分解行为，通过多重速率扫描法，结合多种常用的热分解动力学分析模型，探讨了苯基硅橡胶的热分解动力学，得到如下结论。

（1）苯基硅橡胶在空气中的热分解有一个质量损失平台，热分解温度随着β的增大而提高。

（2）采 用Flynn-Wall-Ozawa 和Friedman 法在不涉及反应机理函数的条件下，分析得到苯基硅橡胶在α为30%～70%时的Ea平均值分别为178.071 8和179.826 8 kJ·mol-1，采 用Kissinger法的最大热质量损失理论公式计算得到苯基硅橡胶的Ea为182.633 kJ·mol-1，3种方法所得的Ea具有较好的一致性。

（3）结合Coats-Redfern法分析得出苯基硅橡胶在空气中热分解反应为三维扩散控制，Coats-Redferm法的理想反应机理函数为g（α）＝[（1＋α）－1/3－1]2。