初中数学四边形教学的解题策略分析

■福建省永春第五中学 姚瑞安

在初中几何中，四边形教学是非常基础且关键的内容，掌握好四边形的解题技巧，能够为更高阶段的几何学习奠定扎实的基础，让学生在学习立体几何的时候更加轻松。笔者将结合具体的数学问题，探究数学解题策略在四边形教学中的应用方法。

一、数形结合策略

数形结合是数学中常用的一种解题策略，经过小学阶段的数学学习，学生已经掌握了一些数形结合的应用技巧，但是没有形成系统的理论概念。所谓数形结合，包括“以数助形”和“以形助数”两个方面，图形的具体、形象的优势集合精准的数字，实现优势互补，使问题更加简单明了。四边形教学中，主要应用到的是“以数助形”的策略，常用的方法有：第一，通过数轴、坐标系把几何问题转化为代数问题。第二，利用面积、距离和角度等几何量来解决问题。

例如，在图1中，梯形ABCD中，BC∥AD，∠A=90°，AB=2，BC=3，AD=4，E为AD的中点，F为CD的中点，P为BC上的动点（不与B、C重合）设BP=x，四边形PEFC的面积为y，求y关于x的函数关系式，并写出x的取值范围。

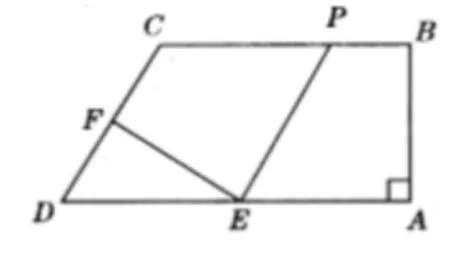
图1

解题思路：因为点P是动点，所以四边形PEFC没有固定的形状，面积也会随着P点的运动而变化，不能套用面积公式，所以要引导学生通过其他图形的面积来计算，通过已知条件，可以求出梯形ABCD的面积，进而利用梯形面积减去△DEF和梯形ABPE的面积就能得出四边形PEFC的面积，其中梯形ABPE的面积是随着P点而变化，所以看似复杂的几何问题实际变成了代数问题，最后要根据P点运动的特殊性——不与B、C重合，求出面积的取值范围。从题干中可以发现，这道题蕴藏明确的数形结合的思想，题目看似复杂，其实就是简单的面积计算问题。教师要引导学生进行归纳总结，使学生之后面对类似的问题时，能够快速厘清思路，提高解题效率。

二、分类讨论策略

有些学生认为，数学问题往往只有一个标准答案，在解题时容易限制自己的思维，利用熟悉的方法去处理和分析问题，往往容易忽略很多关键因素，被一些表面现象所蒙蔽。其实，许多数学问题因为定义、位置和范围的限制，往往不能用统一的方法或标准来解答，而要分情况进行讨论。分类讨论时，学生要具备更宽阔的知识视野，学会处理整体和局部、普遍和特殊的关系，根据题干中给出的信息进行分类，全面而深入地思考数学问题。

例如：已知四边形ABCD中，AD∥BC，AB=DC，AC与BD相交于O，AD=7，BD=10，∠BOC=120°，画出图形并求四边形的面积。

解题思路：根据已知条件，引导学生思考四边形ABCD可能是什么图形，题干并没有指明四边形ABCD的固定形状，因此可以猜想四边形ABCD可能是平行四边形，也可能是梯形，所以需要分情况讨论。第一，当AD=BC时，四边形ABCD是一个平行四边形，如图2；第二，当AD≠BC时，四边形ABCD是一个梯形，如图3。两种情况计算面积，都要充分应用到勾股定理。在解题过程中，教师要引导学生熟练掌握平行四边形、梯形等几何图形的定义，根据题干中给出的条件判断图形的具体形状，学会分类分析数学问题，让学生在有限的条件下充分考虑各种可能，不遗漏任何条件。

图2

图3

三、问题转化策略

转化法也是解决数学问题时常用的一种方法，可以把抽象的数学问题转化成更直观形象的问题。转化方法也可以分为两大类，代数中的转化和几何中的转化，几何中的转化思想常用的有利用合同变换转化、相似变换转换、化归方法转换和形数间的转换。几何教学中，学生在处理不规则图形时往往不知该从何下手，没有固定的公式和规律可以帮助解答。因此，教师要运用转化思想去处理问题，并给学生布置相关的习题训练，让他们学会把复杂的问题转化成简单熟悉的问题，然后利用已有的知识经验去寻找正确答案。通过长期训练，能够增强学生思维的灵活性，促使学生掌握数学知识之间的区别和联系，厘清各种问题之间的逻辑关系。

例如，如图，圆内接四边形ABCD的对角线相交于P点，求证：AB×AD∶CB×CD=AP∶PC。

解题思路：这道题单从四边形角度分析很难得出解题思路，因此最好采用转化的方法，引导学生联想在之前的学习中有没有解答过类似的问题。比如说圆内接三角形的问题，引导学生把不熟悉的题目转化成已知的、熟悉的问题。从求证的内容可以发现，等式两边的次方不同，很可能是等式的右边约去了因式，但很难找出具体约去了哪个因式。对等式进一步分析，发现AB×AD与CB×CD都是相邻两条边的乘积，于是我们可以联想到另外一个题目，如图5，△ABC是圆的内接三角形，AD是△ABC中BC边上的高，AE位△ABC外接圆的直径，求证AB×AC=AD×AE。相对于图4的题目来说，这一题是更容易证明的，只需要连接BE，证明△ABE≈△ADC即可，其实就是证明“三角形两边之积等于其外接圆直径与第三边上的高之积”。用这一题的结论再去证明图4中的例题非常简便。可见，转化思想能有效促进知识迁移，把复杂的问题简单化，提高学生的数学水平。

图4

图5

四、结语

综上所述，教师在课堂上要教给学生数形结合、分类讨论和问题转化等多种解题策略，并且让学生加强有关的习题训练，进一步巩固知识，让学生能够在解决问题时熟练应用这些解题技巧，开放思维，从不同角度分析问题，探究出更多的解题思路。