低维四元局部修复码的构造

展秀珍， 李瑞虎， 付 强， 李沪生， 吕京杰

(空军工程大学基础部， 西安， 710051)

在分布式存储系统中，为了实现数据的可靠存储与恢复，三重备份是简单易行的方案[1]。由于三重备份的存储效率低且存储代价过大，因此人们提出了存储负荷更低的纠删码方案[2-3]。局部修复码是一种新型纠删码，其码字的任一符号位发生故障时，都可通过访问其他固定数目的符号位恢复信息。2012年，Gopalan等人提出局部修复码(Locally Repairable Code， LRC)的概念[4]：若C=[n,k,d]q是码长为n，维数为k，最小距离为d的q元线性码，码字c=(c1,…,cn)∈C的第i(1≤i≤n)位ci都能通过其他至多r位恢复，则称C是局部度为r的局部修复码，并记为C=[n,k,d;r]q。文献[4]还给出Singleton-Like(S-L)界：

(1)

当等式成立时，称码达到了S-L界。特别地，当k=r时，S-L界退化为经典的Singleton界。为了更加精确地描述LRC 4个参数之间的限制关系，2013年Cadambe和Mazumdar提出一个考虑域的大小q的界，即Cadambe-Mazumdar(C-M)界[5]:

(2)

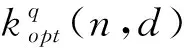
若C=[n,k,d;r]q达到S-L界或C-M界，或者不存在参数为[n,k,d;r-1]q的局部修复码，则称C是局部度最优的(r-最优的)。

在工程应用中，小域上LRC编码和解码复杂度低，从而更具有实用性[6]。Gopalan等人提出LRC的概念之后，人们构造了在小域上达到S-L界[7-10]或C-M界[11-12]的LRC。在四元域上，人们得到一些局部度最优LRC的结果：文献[13]构造了四元LRC[4i+3,3i+1,3;3]4和[4i+4,3i+2,3;3]4(i≥1)。与文献[13]相比，Ernvall等人还构造了参数为[4i+4,3i+1,3;4]4(i≥1)的四元LRC，这三类LRC是局部度最优或拟最优的[14]。Barg等人利用代数曲线和代数曲面构造了参数为[n,k,d;r]q=[18,11,3;2]4的LRC[15]。Fu等利用缩短q元汉明码与(q2+1)-cap构造了d=3,4的四元LRC[10]，其参数为[17-s,13-s,4;11-s]4(0≤s≤5)，[12-j,8-j,4;6-3i-t]4(j=4i+t,0≤t≤3,0≤i≤1)，[21-s,18-s,3;15-s]4(1≤s≤9)和[12-j,9-j,3;6-2i-t]4(1≤j=3i+t≤4,0≤t,i≤2)。文献[16]利用有限域上的自同构群构造一般域上的LRC，可得到参数为[2,1,2;1]4，[4,1,4;1]4，[4,2,2;1]4，[4,3,2;3]4，[3,2,2;2]4和[5,4,2;4]4的四元LRC。

四元域是二元域的二次扩域，四元码能够转化为二元码。当给定码的码长和维数时，四元码的最小距离往往比二元码的最小距离大，即四元码的检错和纠错能力更好，四元距离最优LRC有较好的应用价值。由Grassl的码表[17]和文献[18～20]可得到距离最优四元码，但给定码长和维数时，四元距离最优码往往有很多，它们的局部度也有差别[19]，基于此我们构造局部度较小的四元LRC。设码的维数2≤k≤4，由给定维数的四元Simplex码、MacDonald码以及少量距离最优码的生成矩阵，利用扩展、删除与并置等组合方法，我们设法构造出任意码长n≥k+1且局部度尽可能小的LRC，并利用S-L界及C-M界判断其局部度的最优性。

1 预备知识

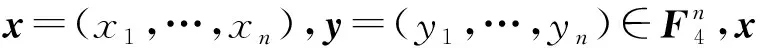
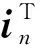
线性码的局部度可以由生成阵确定，具体如下：

引理1[4]设线性码C=[n,k,d]q的生成阵为Gk,n=(g1,g2,…,gn)，gi(1≤i≤n)是k维列向量。对任意i∈[n]，若存在集合Ai⊆[n]{i}使得gi被至多r个gj(j∈Ai)线性表出，则C的局部度为r。

线性码的参数n,k,d相互制约，下面介绍一种重要的码界——Griesmer界。

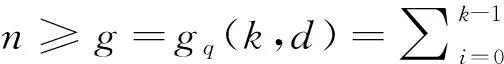
在四元域上，记Sk为k维Simplex码的生成矩阵，Mk为k维MacDonald码的生成矩阵。设k∈Z+，k≥2，则k维首一列向量的个数(即Sk的列数)为nk=(4k-1)/3，显然nk=4nk-1+1。下面介绍Sk与Mk的递归构造。

显然，Sk生成参数为[(4k-1)/3,k,4k-1;2]4的距离最优LRC，Mk生成距离最优LRC[4k-1,k,3·4k-2;2]4。

2 低维四元LRC的构造

由文献[20]可知，对于四元线性码[n,k,d]4，当k=2且给定最小距离d时，存在达到Griesmer界的[n,2,d]4码。当k=3且d=7,8时，有n=g+1；对于其他的d存在达到Griesmer界的[n,3,d]4码。k=4时，若d∈{3,4,7,8}∪[13,16]∪[23,32]∪[37,44]∪[77,80]，则n=g+1；对于其他的d存在达到Griesmer界的[n,4,d]4码。因此本节分3小节讨论四元距离最优LRC[n,k,d;r]4(2≤k≤4)的构造。

约定：四元距离最优码[n,k,d]4简记为[n,k,d]，四元距离最优LRC[n,k,d;r]4简记为[n,k,d;r]。

2.1 [n,2,d;r]距离最优LRC的构造

根据引理1，构造二维四元距离最优码的生成矩阵，并分析其列向量间的线性关系确定其局部度，其中生成矩阵中的列向量均为首一向量。

引理3存在如下参数[n,2,d;r]的距离最优LRC：

1)当3≤n≤9时，存在[n,2,d;2]距离最优LRC；特别地，若n=6,8，还存在[n,2,d;1]距离最优LRC；

2)当n=5l+i，l≥2，0≤i≤4时，存在[n,2,d;1]距离最优LRC。

证明：

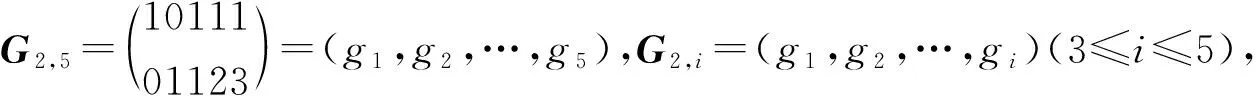
2)当n=5l，l≥2时，令G2,5l=(lG2,5)，G2,5l生成[5l,2,4l;1]码。当n=5l+i≥11，1≤i≤4且l≥2时，由G2,5l+i=(G2,5(l-1)|G2,5+i)可得[5l+i,2,4l+i-1;1]码。

综上可知引理3成立。

以上构造得到所有[n,2,d]距离最优码，其中[3,2,2;2]，[4,2,3;2]，[5,2,4;2]，[6,2,4;1]，[8,2,6;1]，[10,2,8;1]码达到S-L界；[7,2,5;2]和[9,2,7;2]码达不到S-L界或C-M界，但不难验证[7,2,5;1]和[9,2,7;1]不存在，故这两个LRC仍是r-最优的；其余LRC的局部度为r=1，已达到局部度最优。

2.2 [n,3,d;r]距离最优LRC的构造

与2.1节类似，构造三维四元距离最优码的生成矩阵，并分析其列向量间的线性关系确定局部度。

引理4存在如下参数[n,3,d;r]的距离最优LRC。

1)当4≤n≤6时，存在[n,3,d;3]距离最优LRC；当7≤n≤41(n≠32,33)及n=52,53时，存在[n,3,d;2]距离最优LRC；特别地，当n=10,12,28,30,32,33,38,40时，还存在[n,3,d;1]距离最优LRC；

2)当n≥42(n≠52,53)时，存在[n,3,d;1]距离最优LRC。

证明：

1)构造如下4个生成矩阵。

(α1,α2,…,α21)。

以上4个矩阵生成[4,3,2;3]，[9,3,6;2]，[16,3,12;2]和[21,3,16;2]码。令α=(1,2,3)T，β=(1,3,2)T，作G3,5=(G3,4|α)，G3,6=(G3,5|β)，由G3,5和G3,6得[5,3,3;3]，[6,3,4;3]码。由G3,9的子矩阵G3,i=(g1,g2,…,gi)(7≤i≤8)可得[7,3,4;2]和[8,3,5;2]码。由G3,10=(G3,9|γ)，γ∈G3,9可得[10,3,6;2]码。当1≤j≤5时，删除G3,16的后j列得到G3,16-j，G3,16-j生成[16-j,3,12-j;2]码。当1≤j≤4时，删除G3,21的后j列得到G3,21-j，由G3,21-j可得[21-j,3,16-j;2]LRC。

当22≤n≤24时，构造G3,n=(S3|e1,…,en-21)得到[n,3,d;2]距离最优LRC；当25≤n≤30，33≤n≤41时，构造G3,n=(S3|G3,n-21)，G3,n生成[n,3,d;2]距离最优LRC；n=31时，构造G3,31=(M3|G3,15)，G3,31生成[31,3,23;2]码。

特别地，当i∈[5,6]∪[14,16]∪[19,21]时，令A3,2i=(G3,i|G3,i)，A3,2i生成[2i,3,2d;1]距离最优LRC。由G3,33=(A3,32|γ)，γ∈A3,32可得[33,2,24;1]LRC。

2)当43≤n≤63且n≠52,53时，构造G3,n=(S3|G3,n-21)，G3,n生成[n,3,d;1]距离最优LRC。构造G3,52=(S3|G3,31)，G3,53=(S3|A3,32)分别生成[52,3,39;2]和[53,3,40;2]LRC。

当n=21l，l≥3时，令G3,21l=(lG3,21)，G3,21l生成[21l,3,16l;1]码。当n=21l+i，1≤i≤20且l≥3时，令G3,21l+i=(G3,21(l-1)|G3,21+i)，G3,21l+i生成r=1的[21l+i,3,d]距离最优码。

综上可知引理4成立。

以上构造给出所有[n,3,d]距离最优码，当r=1时，局部度已达到最优。当r≥2时，[4,3,2;3]，[5,3,3;3]，[6,3,4;3]，[7,3,4;2]，[8,3,5;2]以及[9,3,6;2]LRC达到S-L界；[23,3,16;2]，[52,3,39;2]，[53,3,40;2]LRC达不到S-L界或C-M界，其余的LRC能达到C-M界。

2.3 [n,4,d;r]距离最优LRC的构造

下面分5≤n≤85，86≤n1≤170，171≤n2≤255和n3≥255四种情形讨论四维LRC的构造。

2.3.1 5≤n≤85时距离最优LRC的构造

由文献[20]知，当k=4时，若d∈{3,4,7,8}∪[13,16]∪[23,32]∪[37,44]∪[77,80]，则n=g+1，对于其他的d存在达到Griesmer界的[n,4,d]码。便于描述，当5≤n≤85时，记达到Griesmer界的[n,4,d]距离最优码的码长构成集合N1,0，且N1,0=[9,10]∪[14,17]∪[25,32]∪[46,50]∪[61,85]。当n∈[5,85]时，若[n,4,d]距离最优码达不到Griesmer界，但[g+85,4,d]距离最优码达到Griesmer界，则记码长n构成集合N1,1=[7,8]∪[12,13]∪[33,44]∪[52,60]；若[g+85,4,d]距离最优码仍达不到Griesmer界，则记码长n构成集合N1,2=[19,24]。

此外，当n=6,11,18,29,32,50,65,71,76,81时，虽然[n,4,d]距离最优码达不到Griesmer界，但存在[n-1,4,d]距离最优码达到Griesmer界；当n=51,66时，存在[n-2,4,d]距离最优码达到Griesmer界；当n=45时，不存在[n-1,4,d]或[n-2,4,d]距离最优码达到Griesmer界。

定理5当5≤n≤85时，存在如下参数[n,4,d;r]的距离最优LRC：

1)存在[5,4,2;4]距离最优LRC；当7≤n≤18及n=33时，存在[n,4,d;3]距离最优LRC。

2)当n=6及19≤n≤85(n≠33,34)时，存在[n,4,d;2]距离最优LRC；特别地，当n=32,34,35,51,56时，还存在[n,4,d;1]距离最优LRC。

证明：

构造以下12个矩阵G4,n，其中G4,17由文献[10]给出，G4,85的6个子块Bi为4×5矩阵。

G4,85=(B1，B2,…，B6|G4,55)=

1)G4,5和G4,10生成[5,4,2;4]，[10,4,6;3]码。当1≤i≤3时，删除G4,10的后i列得到[10-i,4,6-i;3]距离最优LRC。记G4,n=(β1,…,βn)，n=17-j，当11≤n≤17时，G4,n生成[n,4,12-j;3]。由γ∈G4,17，G4,18=(G4,17|γ)可得[18,4,12;3]。当n=33,34时，由G4,n=(G4,17|G4,n-17)可得[33,4,23;3]与[34,4,24;1]码。

2)G4,6生成[6,4,2;2]码。当n=23,28,39,44,49时，G4,n生成[23,4,16;2]，[28,4,20;2]，[39,4,28;2]，[44,4,32;2]，[49,4,36;2]，删除G4,n的后i(1≤i≤4)列得到[n-i,4,d;2]距离最优LRC。G4,31生成[31,4,22;2]码，删除G4,31的后2列得到[n-i,4,d;2]距离最优LRC。当n=31,49时，由G4,n+1=(G4,n|γ)，γ∈G4,n可得[n+1,4,d;2]距离最优LRC。

G4,85生成[85,4,64;2]码，删除G4,85的子矩阵(B1,B2,…,Bi)，1≤i≤6可得[85-5i,4,64-4i;2]距离最优LRC。当n=55,70,75,80,85，1≤i≤4时，删除G4,n的后i列得到的矩阵生成[n-i,4,d;2]距离最优LRC。

考察M4及其子矩阵，M4生成[64,4,48;2]码, 当1≤i≤8时，删除M4的后i列得到[64-i,4,48-i;2]距离最优LRC。

综上可知定理5成立。

2.3.2 86≤n1≤170时距离最优LRC的构造

当86≤n1≤170时，由距离最优LRCC1=[n1,4,d1;r1]和C2=[n2,4,d2;r2]的生成矩阵构造距离最优LRCC=[n1+n2,4,d1+d2;r]的生成矩阵，其中r≤max {r1,r2}，通过删除C的生成矩阵的子矩阵(或列向量)得到新的距离最优LRC的生成矩阵。

定理6记n1=n+85(n∈[1,85])，当86≤n1<170时，存在[n1,4,d;2]距离最优LRC；特别地，当n1=88,98,124,126,128,129,130,140,150,151,156,158,160,161,166,168,170时，还存在[n1,4,d;1]距离最优LRC。

证明：

1)当n∈N1,0,n∈N1,2或n∈[1,5]时，取n∈[1,5]∪[9,10]∪[14,17]∪[25,31]∪[46,50]∪[61,85]∪[19,24]，构造G4,n1=(S4|G4,n)，其中G4,5=(α1,…,α5)及其子矩阵G4,i=(α1,…,αi)(1≤i≤4)，由此可得[n1,4,d;2]距离最优LRC。

2)当n∈N1,1时，结合N1,1的定义，便于描述，记ng=g+85，下面分情况讨论。

①当ng∈[91,93]时，构造G4,ng=(G4,75|G4,n1-75)；当ng∈[96,98]时，构造G4,ng=(G4,80|G4,ng-80)，以上得到的均为[ng,4,d;2]距离最优LRC。

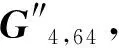
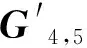
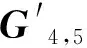
③136≤ng≤144时，构造G4,ng=(M4|G4,ng-64)；当145≤ng≤170时，构造G4,ng=(S4|G4,ng-85)，以上得到的均为[ng,4,d;2]距离最优LRC。

3)特别地，当i=44,49,62,63,64,65,70,75,78,79,80,83,84,85时，令A4,2i=(G4,i|G4,i)，得到[2i,4,2d;1]距离最优LRC。

综上可知定理6成立。

2.3.3 171≤n2≤255时距离最优LRC的构造

类似于2.3.2节，给出码长171≤n2≤255的四元距离最优LRC的构造。

定理7记n2=n+170,n∈[1,85]，当n2∈[176,178]∪[181,183]∪[202,214]∪[222,230]时，存在[n2,4,d;2]距离最优LRC；对于其他码长n2存在[n2,4,d;1]距离最优LRC。特别地，当n=204时，还存在距离最优LRC[204,4,152;1]。

证明：当n∈N1,0或n∈[1,5]时，令G4,n2=(S4|S4|G4,n)，得到[n2,4,d;1]距离最优LRC；当n∈N1,1时，令G4,n2=(S4|G4,n+85)，得到参数为[n2,4,d;2]的距离最优LRC；当n2∈[189,192]时，令G4,n2=(M4|M4|G4,n2-128)，其中G4,61，G4,62与G4,63是M4的子矩阵，得到[n2,4,d;1]距离最优LRC。

特别地，当i=102时，由A4,2i=(G4,i|G4,i)可得[204,4,152;1]距离最优LRC。

综上可知定理7成立。

2.3.4n3≥255时距离最优LRC的构造

由已构造的四元距离最优码构造码长n3≥255的四元距离最优LRC并判断[n,4,d;r](n≥5)距离最优LRC的局部度最优性。

定理8记n3=85i+n，i≥3且n∈[1,85]。若n3∈[274,279]，存在[n3,4,d;2]距离最优LRC；对于其他码长n3存在[n3,4,d;1]距离最优LRC。

证明：

当n3=85i+n(i≥3)且n∈N1,0或n∈N1,1时,令G4,n3=(S4|G4,85(i-1)+n)，得到[n3,4,d;1]距离最优LRC；当n3=85i+n(i=3)且n∈N1,2时，令G4,n3=G4,255+n=(S4|G4,170+n)，得到[n3,4,d;2]距离最优LRC；当n3=85i+n(i≥4)时，令G4,n3=(S4|G4,n)，得到[n3,4,d;1]距离最优LRC。

综上可知定理8成立。

以上构造给出所有[n,4,d]距离最优码，当r=1时，局部度已达到最优。当r≥2时，若n∈[5,10]，[n,4,d;r]为达到S-L界的距离最优LRC;n∈{19,24,33,40,45,66,87,93,114,119,135,145}∪[103,109]∪[176,178]∪[181,183]∪[202,214]∪[222,230]∪[274,279]且n≠204时，[n,4,d;r]为未达到S-L界或C-M界的距离最优LRC; 其余的为达到C-M界的距离最优LRC。

3 结语

结合Grassl码表[17]及文献[20]，对于四元线性码[n,k,d]，根据码的维数分k=2,3,4三种情形构造码长n≥k+1的距离最优LRC。当r=1时，局部度达到最优。r≥2的[n,k,d;r]距离最优LRC的局部度最优性如下：n∈[3,5]时，[n,2,d;2]码达到S-L界，[7,2,5;2]和[9,2,7;2]码达不到S-L界或C-M界，它们仍是局部度最优的；[n,3,d;r](n∈[4,9])码达到S-L界，[n,3,d;2](n=23,52,53)码达不到S-L界或C-M界，其余的LRC达到C-M界；当n∈[5,10]时，[n,4,d;r]LRC达到S-L界，52个LRC达不到S-L界或C-M界。对于以上55个局部度较小仍达不到S-L界或C-M界的LRC，我们未能判定其局部度的最优性，这也是我们接下来要研究的问题。