基于L-Kshape-HACA的空战态势分割聚类

张 鹏， 黄长强， 魏政磊， 周 欢， 王永乾

(1.空军工程大学航空工程学院， 西安， 710038； 2.95596部队，河南商丘，476000)

当前军事装备正向着无人化、智能化的方向发展[1]，制约无人作战飞机作战模式由对地侦查、打击向对空作战转变的主要因素在于自主决策能力不足，过分依赖地面站远程操控，无法满足高动态空战的实时性需求。基于当前空战数据实时提取敌我态势信息来指导无人平台做出自主决策是无人自主空战的关键技术。空战态势知识提取可以转换为近距空战态势模式的发现，其本质是多元时间序列的分割聚类问题。多元时间序列的聚类算法包括两种思路：一种是通过对多元时间序列进行压缩降维，再利用传统的点聚类方法进行聚类[2]；另外一种是结合多元时间序列相似性度量方法改进传统的点聚类方法[3-4]。前者又分为基于特征的聚类和基于模型的聚类，后者为基于初始序列的聚类。基于特征和模型的聚类会忽略原始时间序列的局部特征。基于原始时间序列的聚类一般不对时间序列进行压缩，而是直接进行聚类，该方法随着时间序列增长，其计算代价越大[5]。同时目前的空战态势知识提取文献大多数以空战态势信息到固定态势类别的映射居多，不能体现聚类中心的客观性和态势变化的连续性。

针对以上问题，本文提出了一种基于拉普拉斯中心性和Kshape的分层聚类时序分析方法，解决了多维参数下的态势信息提取问题。

1 基于拉普拉斯中心性的聚类数目确定

目前的分割方法主要是基于特征点的分割和基于监督学习的分割点检测[6-7]。然而实际的时序单元特征无法具体描述或者表示，因此采用基于无监督学习的分割方法是非常有必要的[8]。考虑到传统聚类算法以及基于峰值密度算法(density peak clustering,DPC)[9]的聚类个数无法确定的缺点，本文采用拉普拉斯中心峰值聚类方法(Laplacian peaks clustering algorithm,LPC)[10]，将原始数据转换到加权完全图中，通过构造决策图可以选取聚类个数以及聚类中心；LPC在整个聚类过程中不需要任何经验参数，因此LPC也是一种无参数聚类算法。

1.1 相关参数定义

敌我双方的态势信息主要取决于空战中双方的相对运动关系，如表1所示。

表1 态势描述参数

假设以我机质心为坐标原点O，X轴沿UCAV纵轴指向机头方向，Y轴垂直于UCAV对称面并值向右，Z轴位于UCAV对称面并垂直于机体纵轴向下，我方UCAV与敌机位置坐标为Pu=[xu,yu,zu]和Pe=[xe,ye,ze]，则双机相对态势定义见图1。

图1 空战几何关系

假设原始未分类的空战态势描述参数数据集为Xs={Xs,1,Xs,2,…,Xs,tn}，其中Xs,i=[Ri,Δhi,vu,i,φu,i,qu,i,ve,i,φe,i,qe,i]，i=1,2,…,tn，tn为获取的空战数据末端时间点。为了挖掘聚类中心，定义2个主要指数：第i个数据点的拉普拉斯中心性ci和最小距离值δi。其次，将数据集转换为加权完全图G=(Xs,E,W)，将每个数据点看作加权网络E的节点，W表示边权值的集合。具体定义如下：

定义1相异度矩阵W。wi,j是数据点Xs,i与Xs,j之间的边权值，用于衡量多元时间序列相似性。由于原始态势参数序列不等长且具有高动态性，本文采用动态时间弯曲距离法(dynamic time warping，DTW)[11]进行计算。

(1)

定义2和对角矩阵Z：

Z(G)=diag(z1,z2,…,zn)

(2)

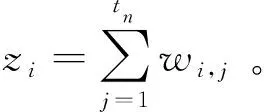
定义3拉普拉斯矩阵L：

L(G)=Z(G)-W(G)

(3)

定义4拉普拉斯能量EL(G)：

(4)

式中：λ1,λ2,…,λtn为拉普拉斯矩阵L(G)的特征值。

定义5拉普拉斯中心性ci。在加权完全图G中，删除节点Xs,i以及与其相连的边，得到的加权完全图为Gi。节点Xs,i的拉普拉斯中心性ci可以定义为：

(5)

式中：EL(Gi)表示删除节点Xs,i之后的加权完全图的拉普拉斯能量，拉普拉斯中心性的意义在于删除当前节点后的拉普拉斯能量相对下降。当前节点拉普拉斯中心性越高，则该节点重要程度越高[11]。

定义6最小距离值δi。对于当前节点Xs,i，通过比较拉普拉斯中心性ci，可以得到最小距离值δi，其具体计算如下：

δi=

(6)

1.2 基于正态分布“3σ”准则的聚类个数提取策略

根据上述定义的分析，具有较高最小距离值和较高拉普拉斯中心性的数据节点可以作为聚类中心，由此可以确定聚类个数。利用最小距离值δ和拉普拉斯中心性c构造决策图[12]。为了自动完成这一过程，本文采用了基于正态分布“3σ”准则的聚类个数提取策略。为了从数据节点中自动提取聚类个数，引出另外一个决策量γ，其定义如下：

γi=ci·δi

(7)

为了方便提取聚类中心与聚类个数，对γ值进行放大：

(8)

式中：Eγ,i为节点Xs,i由决策量γi放大后的值。

假设数据节点的扩大后决策值Eγ服从正态分布，根据正态分布的“3σ”准则，将(μ-3σ,μ+3σ)区域看作该随机变量实际可能的取值区间。由于潜在的聚类中心的决策值Eγ远大于非聚类中心的Eγ值，可以得到Eγ值大于μ+3σ的数据节点。图2给出基于拉普拉斯中心性的决策图，其中红色的数据节点为Eγ值大于μ+3σ的数据节点，即聚类中心，因此聚类个数为3。

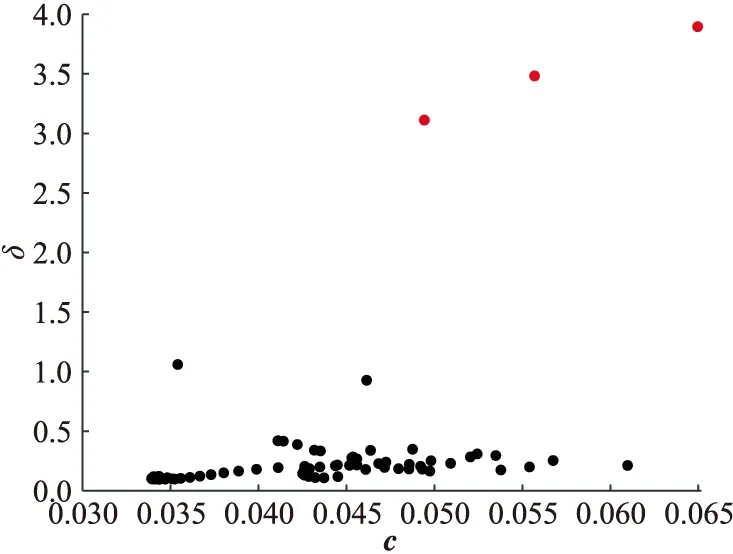
图2 某空战态势描述参数决策图

2 基于拉普拉斯中心性的聚类中心确定

时间序列的聚类算法的提出主要来源于2种途径[13]：第1种是替代相似性度量方法，属于基于原始数据的聚类方法；第2种是将时间序列转换为静态数据，包括基于特征和基于模型的聚类方法。基于特征和基于模型的聚类方法是对原始时间序列进行特征提取或者模型表示，不能体现出时序信息。本文选择基于原始数据的时间序列聚类方法，其主要依赖于矩阵的分解。

针对以上问题的分析，本文提出了一种基于原始数据的多元时间序列聚类方法，即Kshape。首先，提出一种基于互相关度量的形状距离度量方法；其次，基于形状距离度量方法，设计一种计算时间序列聚类中心的计算方法；最后，根据相似性度量方法与聚类中心计算方法，给出了基于Kshape的多元时间序列聚类算法具体步骤。

2.1 时间形状相似性度量方法

为了提高时间序列相似性度量计算效率，本文设计了一种互相关度量方法。

对于序列Xs={Xs,1,Xs,2,…,Xs,n}与Ys={Ys,1,Ys,2,…,Ys,m}，为了实现位移不变性，固定时间序列Ys不动，滑动Xs，互相关度量就是计算滑动过程中对齐的元素之间的内积。Xs时间序列的移位序列计算表达式为：

(9)

式中：Xs(κ)表示移位κ之后的时间序列。一般情况下，κ∈(-n,n)或者κ∈[-n+1,n-1]。假设n=3，那么其移位时间序列的个数为2n-1=5，为了方便理解，给出示意图见图3。移位序列中，Xs(0)就是原始时间序列，其他移位序列的某些元素需要填充为0。

图3 移位时间序列

根据移位序列Xs(k)，可以得到互相关序列CCω(Xs,Ys)=(c1,c2,…,cω)，其长度为2n-1，与移位序列的个数相等。互相关序列可以定义如下：

CCω(Xs,Ys)=Rω-n(Xs,Ys)

(10)

式中：ω∈{1,2,…,2n-1}。同时，Rω-n(Xs,Ys)的计算公式如下：

(11)

通过计算式(10)中的CCω(Xs,Ys)中最大的互相关序列值，得到对应的ω。基于ω值，可以得到κ=ω-n，对应的移位序列Xs(κ)是最优的匹配序列。由于问题的不同，则采用的标准化方法不同。本文选取了文献[15]中的系数标准化方法，即NCCc，具体定义如下：

(12)

式中：NCCc(Xs,Ys)的值域为[-1,1]。NCCc(Xs,Ys)=1说明两个时间序列相似，NCCc(Xs,Ys)=-1说明两个时间序列负相关。

为了设计一种基于形状距离的度量方法，将NCCc(Xs,Ys)取值映射到[0,2]，具体计算公式如下：

SBD(Xs,Ys)=

(13)

为了提高基于形状距离(shape-based distance,SBD)的相似性度量计算过程，采用Xs与Ys离散傅里叶变换内积的离散傅里叶逆变换计算[14]。具体的计算公式如下：

CC(Xs,Ys)=F-1{(Xs)(Ys)}

(14)

(15)

(16)

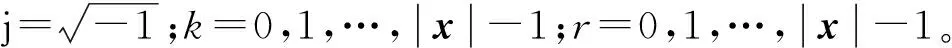
2.2 聚类中心提取策略

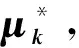
(17)

代入到式(17)中，得到：

(18)

2.3 基于Kshape的多元时间序列聚类

基于SBD度量方法与聚类中心提取策略的Kshape聚类算法类似于k-means，可以更新得到聚类划分较好的聚类中心，且可以有效地处理时间序列的缩放、平移、转移不变性。Kshape聚类过程是一个迭代寻优的过程，主要的步骤为：①时间序列样本分配过程：根据聚类中心，分配时间序列Xs到距离最近聚类中心；②聚类中心更新过程。依据上一迭代中聚类关系的变化，重新计算聚类中心。Kshape算法重复步骤①与步骤②，直到聚类关系不再发生变化(各类别样本到聚类中心的SBD距离平方和不再发生变化)或者达到最大迭代次数。

3 分层聚类时序分析

从一组空战数据中寻找态势时序单元(未知)是一个多元时间序列分割聚类问题。时间序列的分割聚类是一种非监督学习问题，主要应用于计算机视觉与计算机图形学[15]。空战态势描述参数具有时序性，也具有空间性，可以分解为多种态势时序单元，目前面临的问题主要体现在：①态势时序单元组合呈指数增长；②每个相同场景的态势描述参数时间序列不一样，具有时间的伸缩性；③态势时序单元划分粒度可变性。

针对以上问题，本文提出了一种分层的聚类时序分析方法(HACA)。该方法结合聚类算法与分割算法，提出坐标下降法在计算分割段以及其聚类过程中选择求解。

3.1 聚类时序分析方法

假设给定多元时间序列Xs={Xs,1,Xs,2,…,Xs,n}，其中Xs∈Rd×n，n为时间序列的时间长度，d=8 表示态势描述参数的维度。将Xs分割为mc个态势时序单元，其中每个单元对应k聚类类别中的某一类。假设第i个分割态势时序单元Yi=Xs,[si,si+1)=[xsi，…,xsi+1-1∈Rd×n]，该态势时序单元的开始时刻为si，结束时刻为si+1-1，其长度ni=si+1-si必须满足ni≤nmax，其中nmax为态势时序最大长度且控制时间序列分割粒度。为了方便表示与计算每个态势时序单元的所属类别，则定义聚类指示矩阵G∈{0,1}k×mc，其中聚类指示矩阵元素gci=1表示Yi属于类别c，否则gci=0。结合第2节的时间序列聚类算法Kshape，基于聚类时序分析的聚类分割方法目标函数为：

SBD([Y1,…,Ymc],UcG)

s.t.GT1k=1mandsi+1-si∈[1,nmax]

(19)

式中：G∈{0,1}k×mc为聚类类别指示器，s∈Rmc+1为态势时序单元的分割起始点与末端点时刻，Yi=Xs,[si,si+1]表示第i个分割段(态势时序单元)，Uc={u1,u2,…,uk}为聚类中心集合。本文采用的多元时间序列相似性度量方法为基于形状距离(SBD)的度量方法。

式(19)是一个关于G和s整数规划问题。根据上述的定义，G表示态势时序单元与聚类中心的指示矩阵，s表示态势描述参数点与态势时序单元之间的对应关系，优化关于G和s的聚类分割方法目标函数是一个非线性多项式NP难问题。为了解决该问题，本文采用坐标下降法框架，利用动态规划策略来优化计算s，利用winner-take-all策略来优化计算G。每一迭代次数具体优化如下表示：

(20)

式中：uc是类别为c的聚类中心，该聚类中心可以由基于SBD的聚类中心提取策略，由上一迭代次数的解(G′,s′)得到。式(20)的计算复杂度随着原始时间序列的增长而增加，因此，本文采用了一种基于动态规划的算法去检测可能的态势时序单元。为了进一步提高求解(G,s)的效率，引入一种辅助函数：

计算机作为高新技术应用，对于提高学生社会实践能力及计算机技术水平具有良好的推动作用。尤其是极域多媒体电子教室软件应用，对解决计算机基础性教学的诸多难题有一定的帮助，使学生在计算机知识学习方面，不再受到基础学习环境及知识学习能力的限制，实现对学生计算机知识的立体化教学。通过理论知识讲解与教学实现对学生计算机知识的掌握能力及应用能力进行深度提高。

(21)

式中：Xs,[i,v]=[x1,x2,…,xv]表示末端时刻为v的态势时序单元，通过优化求解v来替代优化求解s。利用动态规划的思想，可以将式(21)改写为：

J(v)=

(22)

式中：时间序列Xs被划分为Xs,[1,i-1]与Xs,[i,v]，优化公式(22)使其最小化，得到最优的子序列Xs,[1,i-1]与Xs,[i,v]。尽管分割时间序列Xs的可能情况随着时间序列的时间长度增加n，但动态规划方法利用Bellman方程解决最优问题仍然是一个有效的方法。

J(v)=

(23)

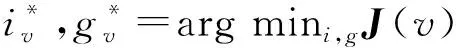
步骤2后向过程。根据步骤1中得到的最优分割点位置与聚类类别，从右向左依次划分，通过计算得到s与G。

重复步骤1与步骤2直到J(n)收敛不变或者迭代次数达到最大。

3.2 分层策略

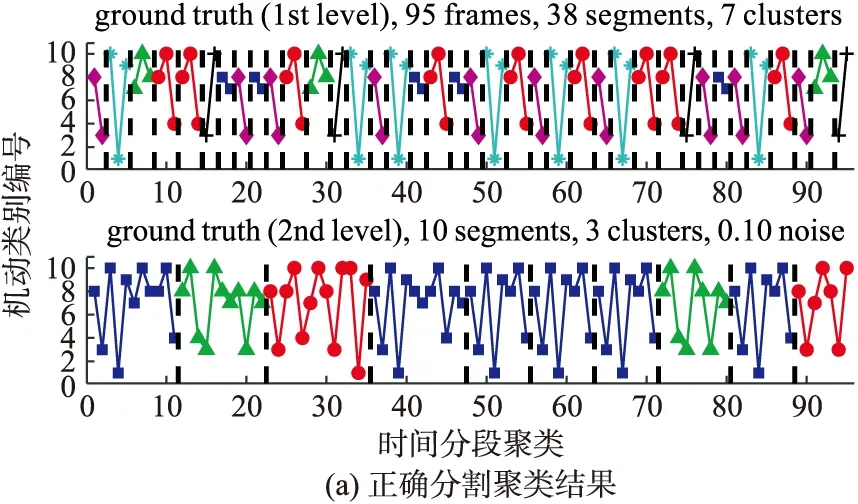
图4 分层聚类时序分析结果对比

4 基于L-Kshape-HACA的分层聚类时序分析仿真

结合基于拉普拉斯中心性的聚类个数确定方法与基于Kshape的多元时间序列聚类算法，本文提出了一种基于L-Kshape的分层聚类时序分析方法(L-Kshape-HACA)，用于解决长时域态势描述参数序列的分割聚类问题。L-Kshape-HACA分割聚类方法流程图如图5所示，其中迭代停止标准均为J(n)不再发生变化或者达到最大迭代次数。

图5 基于L-Kshape-HACA的分层聚类流程图

态势聚类的有效性是实现正确的近距空战决策的数据基础。为了验证L-Kshape-HACA分割聚类方法解决近距空战态势描述参数态势时序单元提取问题的可行性与有效性，利用基于贝叶斯推理的态势评估方法[16]、基于多维点数据的聚类算法(聚类数据由多维空间中点数据组成)、基于模型表示的时间序列聚类算法和于多元时间序列数据的分割聚类算法与L-Kshape-HACA分割聚类算法进行比较。为了对比基于数据驱动的态势聚类分析与基于推理的态势评估，本仿真实验的对比算法包括文献[16]中基于贝叶斯推理的态势评估方法；为了对比基于时序数据的态势聚类与基于点数据的态势聚类，本仿真实验比较的基于点数据态势聚类算法还包括自组织特征映射神经网络(self-organizing feature map,SOM)[17]、层次聚类(hierachical clustering,HC)[18]、模糊C均值的态势聚类[19]、高斯混合的态势聚类[20]、k-means、DBSCAN以及文献[9]中基于密度峰值的态势聚类；为了比较基于分割聚类的时序态势知识提取方法的好坏，本仿真实验比较的分割聚类方法包括ACA[8]、基于谱聚类的分层ACA(HACA)[16]、基于k-means的分层ACA(k-means-HACA)以及基于密度峰值的分层ACA(DPC-HACA)；除此之外，为了测试基于拉普拉斯中心性聚类个数的确定方法是否有效，则需要比较基于Kshape的分层ACA(Kshape-HACA)。本文仿真实验数据来源于某近距空战模拟训练的对抗数据，该实验选取其中的12组近距空战对抗数据，其皆为红方(我机)获取胜利的数据，实验仿真环境为Windows 10，CPU为2.80 GHz,8 GB内存，编程语言Matlab。

表2 L-Kshape-HACA不同时序分割最大值设置

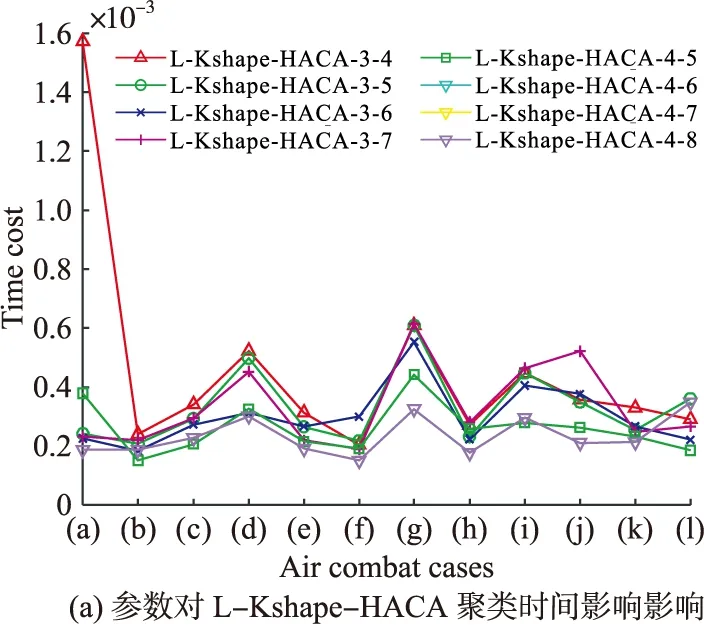
图6 不同时序分割长度最大值的影响

基于L-Kshape-HACA分割聚类方法与比较算法的仿真测试结果如图7和图8所示。

本文选取了4组空战对抗数据进行了对比，图7给出了基于L-Kshape-HACA分割聚类算法与其他算法的时间序列分割聚类示意图，不同的颜色表示不同的类别，可以看出，与基于先验知识贝叶斯推理的态势评估结果相比，基于L-Kshape-HACA的态势描述参数序列分割聚类结果是最接近的。图8给出了态势描述参数归一化之后的特征空间，可以看出，整个态势描述空间可以聚类为4类，态势描述参数序列可以分割为9个态势时序单元。为了表达这种抽象的态势时序单元，结合基于贝叶斯推理的态势评估结果，根据图8所示的对抗轨迹分割聚类结果，得到以下态势时序单元特征：1)Cluster #1：我机其他状态-互不安全的转换；2)Cluster #2：我机中立互为安全-守势-中立相向状态的转换；3)Cluster #3：我机攻势-互为安全状态的转换；4)Cluster #4：我机互不安全-攻势状态的转换。

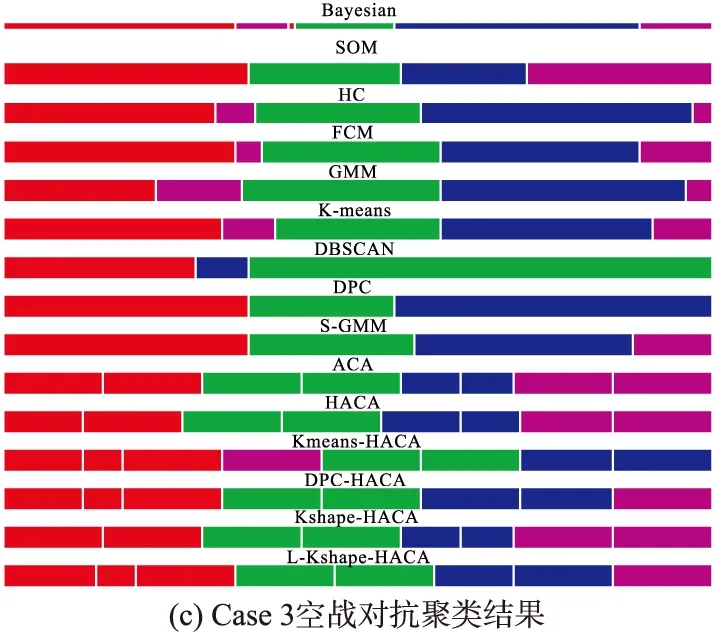
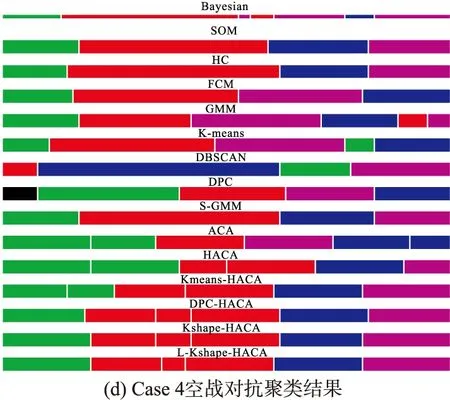
图7 L-Kshape-HACA与比较算法的分割聚类结果对比

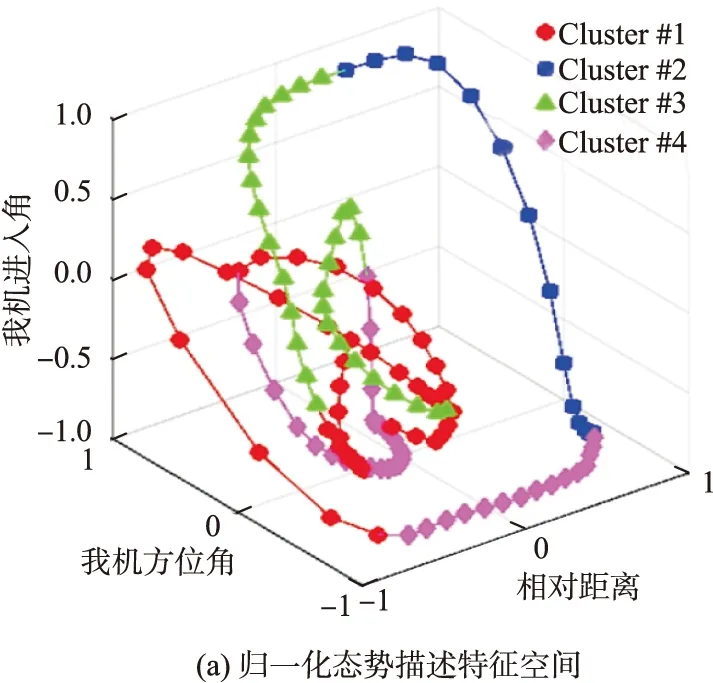
图8 Case(2)空战对抗组的态势时序单元分析

5 结语

无人自主空战是未来智能作战的关键技术，本文设计了一种基于数据的无监督态势信息提取新方法，为无人空战决策提供了更加客观可靠的数据基础。本文研究的泛化分析算法会在态势提取过程中忽略飞机独有的战术机动性能，因此，下一步研究必须要针对特定机型的空战数据进行研究，从而提高战术机动态势提取的准确度。