针对逃逸目标的多机协同围捕策略研究

周贞文, 邵 将, 徐 扬, 罗德林

(1.厦门大学航空航天学院，福建厦门，361102；2.钱学森空间技术实验室，北京，100094；3.哈尔滨工业大学卫星技术研究所，哈尔滨，150001；4.西北工业大学民航学院，西安，710072)

无人机(unmanned aerial vehicle，UAV)具有低成本、机动性能强、风险较低等优势，在军用和民用领域都被广泛应用。随着无人机应用场景更加复杂和任务需求难度加大，单架无人机已经无法完成一些作战任务，需要多架无人机协同工作，才可以快速完成任务[1-3]。因此，多无人机协同工作是目前无人机研究领域的一个热点。

随着无人机技术的发展，以无人机为主要应用对象的集群系统[4-5]通过无人机之间的通信网络，共同完成侦察、追踪、打击等复杂的协同任务将成为未来无人机集群的重要作战模式[6-7]。根据群智能体在不同的场景中的应用，应用类型可以分为多机协同路径规划[8]、多机协同目标搜索[9]、多机编队飞行[10]、多机协同作战[11]等。多架无人机协同飞行执行任务在现代战场中的应用得最为广泛[12]。

现有研究中，一种通用的研究思路是将多对多作战任务解耦为一对一对抗过程。在文献[13]中通过影响图建立了无人机协同作战的连续决策模型，并将作战过程分解为态势评估、目标分配和机动决策三个步骤，然而该方法只适用于敌我双方目标数量相同的作战情形。通过引入基于个体行为集的多智能系统理论[14]，将每架无人机视为一个独立的智能体，在其各自环境的作用下可达到协同作战的效果，该方法的优势在于可任意设置双方参战飞机的数量，但是随着无人机数量的增多，算法复杂度也将急剧增大。陈侠[15]根据无人机空战攻防参数的不确定信息建立了敌我双方攻防的模糊支付博弈模型，结合模糊结构元方法和粒子群算法给出动态博弈的多无人机空战最优作战策略，但是这种静态博弈模型与实际瞬息万变的动态空战过程不符。在多机协同围捕逃逸目标的实战任务中，通常是雷达监测系统发现不明飞行目标非法进入我方领空后，我方派出多架飞机，以一定队形对目标进行围捕，根据不同的入侵程度和任务指令，对目标展开伴飞、驱离、逼停降落等非战争攻击行为。在文献[16]中, 通过分析鹰群狩猎中的集群行为，建立了仿鹰群智能的集群对抗模型，利用基于Lyapunov导航向量场的导航法则，使各架无人机以期望速度收敛到目标轨迹上，进而实现对敌方无人机的合围攻击。

受上述讨论启发，从多无人机协同对抗任务到自然界目标逃逸、狩猎者围捕展现的群体行为出发, 本文提出一种多无人机协同围捕逃逸目标策略。策略的第1阶段用于跟踪目标，一种基于动态反馈线性化控制方法可确保无人机集群以预定构型包围运动目标。在第2阶段引入李雅普诺夫矢量场(lyapunov vector fields, LVF)，使无人机在飞行中可以安全绕过禁飞区等危险区域。

1 问题描述

1.1 无人机运动模型

考虑无人机的平面围捕目标的飞行情形，无人机UAVi的运动模型可简化为：

(1)

式中：(x,y)为无人机的位置坐标；vi为无人机的飞行速度；φ为飞行航迹角；vc为飞行速度控制量；τv和τφ为时间常数因子。受无人机性能的影响，飞行速度和转弯角速度约束可建模为：

(2)

式中：vmax为无人机最大飞行速度;wmax为无人机最大转弯角速度。

1.2 敌我态势描述

为了明确本文所提出的多机协同围捕逃逸目标策略的应用场景以及前提条件，做以下说明：

1)本文所提出的协同围捕策略，是针对非法入侵我方领空的他方飞机进行包围驱逐或伴飞监视等非战争性质的应用场景；

2)围捕目标所在位置可由我方地面雷达监测系统或无人机机载雷达进行探测，并实时传递共享；

3)提出的围捕策略模型是基于假设我方无人机飞行速度比目标无人机的飞行速度更占优势，是模拟在实际的边界环境或者禁飞领空区域中，使用无人机对非法闯入的他方飞机进行包围驱离的应用场景。

图1 无人机集群与目标敌机的相对位置

dp=‖χr-χi‖

(3)

(4)

1.3 围捕逃逸目标策略判定

基于逃逸目标围捕策略的无人机集群围捕敌机的流程如图2所示。

图2 无人机集群围捕逃逸目标的流程图

首先，地面雷达监测系统将敌机的实时坐标位置传送给作战无人机集群，指挥部下达指定的围捕目标的飞行队形；无人机集群接受到相关数据信息后，通过动态反馈线性控制器得到飞行的期望位置；通过机载雷达传感器的实时探测数据，计算判断出无人机的前方是否会出现飞行障碍区或者威胁区，若存在，则计算判断出雷达威胁源的方位，选取对应的LVF旋转矢量场进行绕飞控制，得到无人机期望飞行的实时方位。

无人机采取图1所示的菱形队形进行围捕，前机用于拦截敌机加速向前逃逸，左右两机对敌机形成夹击之势，防止敌机转向逃跑，而尾部无人机则是占据有利的攻击位置，能够随机监视了解敌机动态，并且可以锁定敌机，随时摧毁敌机。

1.4 围捕终止条件

当无人机与敌机的飞行速度、航向、相对距离保持一致，且无人机之间的相对位置距离保持稳定，相对位置角度保持不变时，即满足以下围捕条件时：

(5)

判定无人机集群已形成了针对目标的稳定围捕队形，多机协同围捕任务完成。

2 动态反馈线性控制

飞行控制器设计可使我方无人机之间的距离和航向角保持一致稳定[17]，无人机集群与逃逸目标的相对位置保持静止。无人机集群围捕队形是每架无人机以逃逸目标的飞行位置和速度为期望值，然后各架无人机之间的飞行位置角度保持一致，达到一个稳定的围捕构型。设定无人机的二维空间内的飞行控制律ux，uy分别为：

(6)

式中：kp、kv、ka分别为位置反馈增益因子、速度反馈增益因子和加速度增益因子。

通过控制律可得到的无人机集群的飞行速度控制量vc和飞行角度控制量φc：

(7)

根据无人机的飞行动力学方程，将控制量vc和φc代入式(1)获取无人机集群的下一步飞行坐标位置。

基于动态反馈线性控制方法求取逃逸目标飞行状态的具体实现步骤为：

Step1根据无人机接收到的逃逸敌机飞行状态χr(xr,yr,vr,φr)，由式(6)得到无人机集群二维空间的飞行控制律ux,uy；

Step2将控制律代入式(7)中，得到无人机χi的飞行速度和角度的控制量vc和φc；

Step3将控制量vc和φc代入无人机的运动方程式(1)中，得到无人机下一步飞行状态χi(xi,yi,vi,φi)；

Step4跳转返回到Step1，直至围捕任务结束。

3 躲避雷达威胁源

3.1 威胁源绕飞模型

在实际的作战飞行空间中，通常存在敌方雷达和防空火力威胁，为了确保我方无人机的安全飞行，需要针对敌方雷达源等禁飞区采取绕飞躲避操作。在图3中，为保障无人机的飞行安全，以无人机的实际机身面积作为无人机在飞行过程中的最大雷达反射面积[18]。在计算雷达扫描威胁范围时，可以在雷达扫描半径Ro的基础上向外膨胀扩展一个机身宽度Rs，以确保无人机安全避开威胁区域。

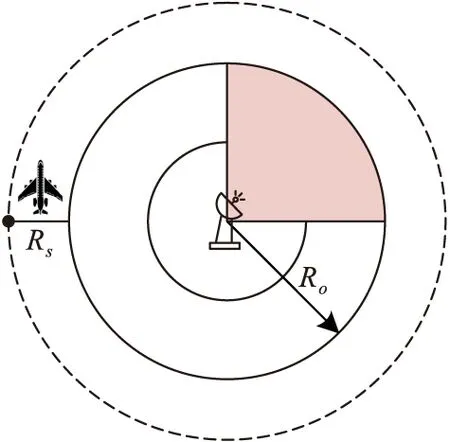
图3 雷达威胁模型

无人机对逃逸目标进行围捕的飞行过程中，需要通过机载雷达传感器发现威胁源的具体坐标位置，从而提前采取有效的绕飞措施，如图4所示。假设无人机机载传感器的有效探测距离为Rt，通过计算无人机的位置与雷达威胁源的距离以及无人机航迹角与雷达位置的相对角度，可以计算出无人机在飞行过程中会不会进入威胁区域，从而判断是否需要绕飞。

图4 传感器探测雷达模型

无人机飞行过程中，可通过下式判断是否需要绕回：

(8)

由此可知，当满足Rtsinβ≤(Ro+Rs)条件时，无人机需要绕飞，即f=1，反之则无需绕飞。

3.2 李雅普诺夫矢量场

张毅[18]基于LAWRENCE D[19]提出了李雅普诺夫矢量场概念，定义了李雅普诺夫函数为：

(9)

duo=

(10)

dr=Rs+Ro

(11)

式中：duo为无人机与雷达威胁源的欧式距离；dr为无人机位于矢量场的期望绕飞飞行半径。

显然，VF(χ)>0是正定函数，由式(8)可以定义出LFV矢量场的速度分量式为：

(12)

(13)

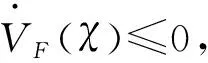
进一步，通过坐标分解，可以得到矢量场顺时针旋转方向速度：

(14)

当根据式(7)判断出敌方雷达后，无人机需绕飞躲避威胁源。而通过计算无人机飞行位置与雷达的方位角，判断出雷达威胁源是位于无人机前进方向的左侧还是右侧，进而选择具体的矢量场方向速度式进行绕飞控制。如图5所示，穿过雷达威胁源并垂直于无人机前进方向的直线与威胁区域边界交点为与p1、p2，2个交点与无人机前进方向的相对夹角分别为α1、α2。考虑到无人机转弯避障时的机动性能和飞行油耗，选择方向角改变量小的方向进行转弯避障。

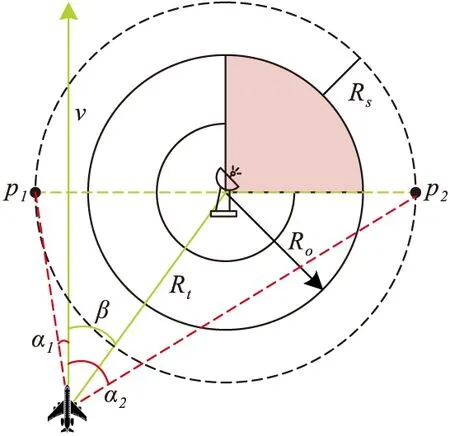
图5 最优绕行方向的选择

当雷达威胁源位于无人机飞行航向的右边时，无人机需要进行顺时针转弯避障，选取式(12)的逆时针旋转矢量场速度分量，此时控制量为：

(15)

3.3 绕飞结束判定

在本文中，李雅普诺夫矢量场生成一个引力作用磁场，如图6所示。当无人机在引力场中进行避障飞行时，需要实时判断出避障飞行的结束位置，从而摆脱LVF的吸引力作用，以避免无人机过度受引力的影响，飞行远离目标位置。当无人机的飞行位置航向与雷达威胁源方位的夹角γ≥90°时，即可认为无人机成功绕开了雷达威胁区域，可以摆脱LVF矢量场的引力作用。

图6 绕飞结束判定

4 仿真实验

4.1 无人机躲避威胁源

首先验证LVF矢量场对于无人机绕开威胁区域的有效性，以一架无人机分别对于不同的飞行环境进行仿真实验。

在图7、8中，紫色五角星标记为无人机的起飞位置，紫色圆形标记为无人机的飞行结束位置。红色圆形区域为雷达扫描探测范围，红色虚线为辐射范围向外膨胀一个机身宽度，绿色实线为无人机的飞行轨迹。无论是针对敌方雷达疏松部署还是密集部署的飞行环境，当机载传感器探测到雷达的位置时，无人机在LVF矢量场的引力下，能够及时绕开威胁区域，安全到达终点。

图7 无人机躲避一个威胁源的飞行轨迹

图8 无人机躲避多个威胁源的飞行轨迹

4.2 逃逸目标围捕

为验证本文提出的逃逸目标围捕策略的可行性和有效性，本文采用4对1的围捕实例进行仿真实验。

4.2.1 仿真实验1

为了能够清晰明了地展示实验仿真过程及效果，设定为四旋翼等飞行速度较慢的无人机进行验证，以便于详细展示无人机的在围捕飞行过程中的细节。假设无人机集群同时起飞，逃逸敌机则以恒定的飞行速度和角速度进行逃逸飞行，仿真实验的具体参数如表1所示。

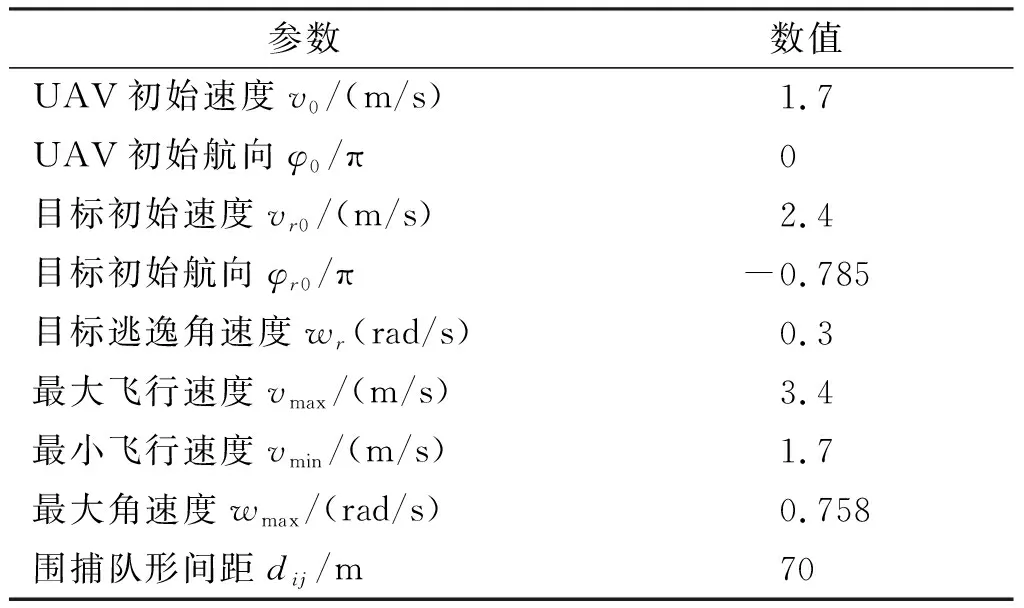
表1 多无人机协同围捕逃逸目标实验参数

我方无人机集群采取图1所示的正菱形的围捕队形，无人机之间的间距dij=70 m。图9为无人机集群在存在雷达威胁的飞行环境中围捕逃逸敌机的飞行轨迹。其中，橙色的圆形区域为敌方雷达的辐射范围，圆形图标为无人机与敌机的最初位置。根据预警机传送的敌机位置，通过LVF旋转引力场,我方无人机集群，能够安全躲避雷达威胁源，及时调整飞行航向及速度，快速向逃逸目标飞去。在400 s时，无人机集群成功围捕逃逸敌机，如图9所示。

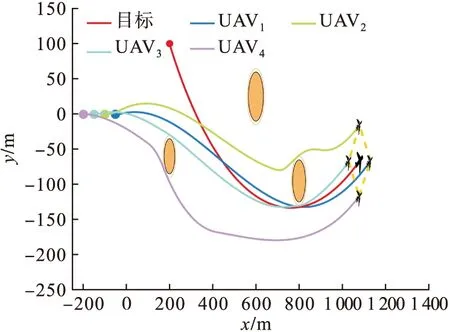
图9 仿真1中多无人机协同围捕逃逸目标飞行轨迹

图10(a)展示了为无人机集群与逃逸敌机的位置距离dp变化情况，在400 s左右，无人机集群与逃逸敌机的相对距离收敛为一个定值，对应图9中我方无人机成功围捕到目标敌机。图10(b)为无人机集群围捕队形的空间距离dij变化，无人机在围捕逃逸目标的飞行过程中，逐渐缩小dij，最终达到稳定的围捕队形。图10(c)～(e)为无人机集群与目标敌机在围捕-逃逸的飞行过程中的飞行速度、飞行航向角和角速度的变化。由图中数据可知，UAV2和UAV4分别在260 s和120 s时进行雷达躲避飞行，因而出现了实验数据的剧烈变化现象。在400 s后无人机集群与敌机的飞行参数收敛至稳定数据，无人机以稳定的队形将逃逸敌机成功围捕。

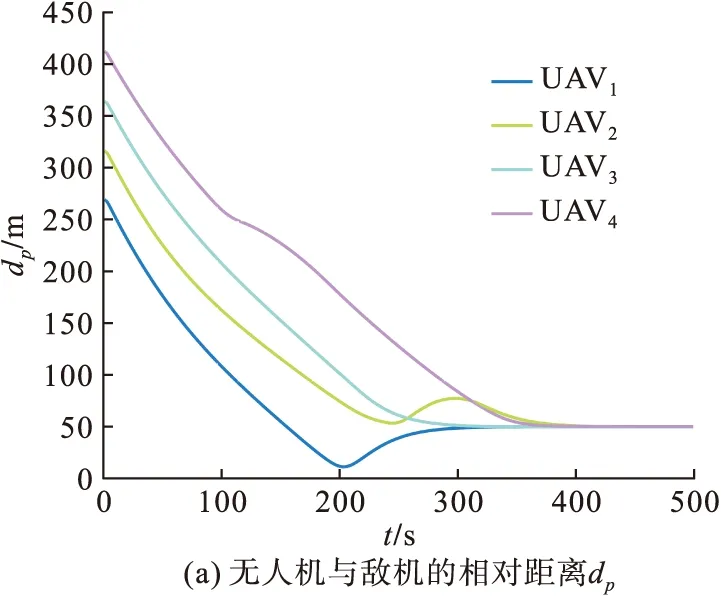
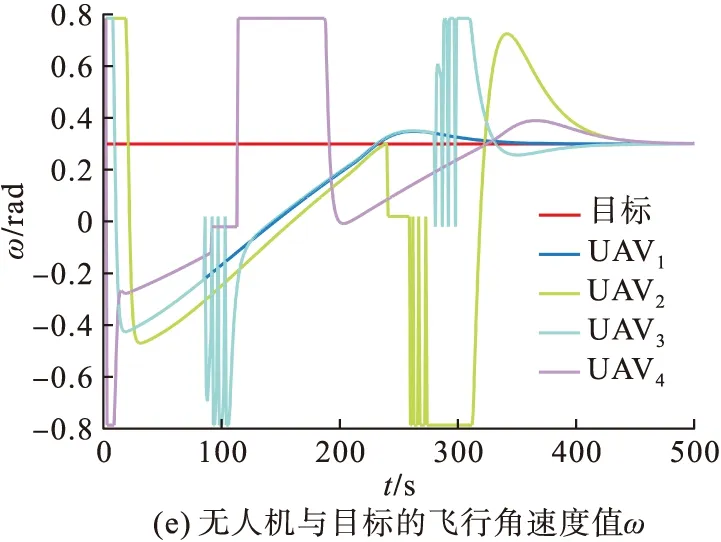
图10 多无人机协同围捕逃逸目标仿真实验数据

4.2.2 仿真实验2

为了验证逃逸目标围捕策略在实际作战环境中的可行性，将无人机的飞行参数设置为固定翼无人机参数进行仿真实验。设置无人机的最小飞行速度为100 km/h，最大飞行速度为217 km/h，目标敌机的飞行速度为135 km/h。无人机的最大角速度为0.35 rad/s，目标敌机以随机航线变化进行逃逸飞行。实验仿真结果如图11所示。

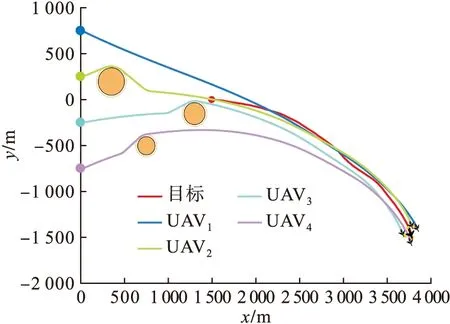
图11 仿真2中多无人机协同围捕逃逸目标飞行轨迹

由图可以看出4架无人机成功避开了飞行过程中遇到的障碍，并最终成功围捕了逃逸目标。仿真结果表明本文所提的围捕策略可行、有效。

5 结语

本文设计了一种可实现多对一的集群无人机协同逃逸目标围捕策略。基于动态反馈线性化控制器，使用控制器设计出的无人机飞行的控制律，使我方无人机集群快速跟踪到逃逸的敌机，并最终形成稳定的围捕飞行队形；在形成围捕队形的飞行过程中，基于LVF旋转引力矢量场来确保无人机及时躲避飞行障碍区域和威胁区域，完成绕开威胁源飞行后，迅速返回编队飞行状态。

通过以敌我双方4对1的追击围捕场景进行了仿真实验研究。仿真结果数据验证了本文提出的无人机集群协同逃逸目标围捕策略的有效性。