气动弹性效应对超高层建筑横风向动力干扰效应的影响
侯方超, 全 涌, 顾 明
(1. 同济大学 土木工程防灾国家重点实验室,上海 200092;2. 东莞市厚街镇工程建设中心,广东 东莞 523000)
随着建筑高度的增加,超高层建筑的横风向风致响应通常超过顺风向风致响应成为设计中的控制性响应[1]。当高层建筑周边存在干扰建筑时,由于气动干扰效应,高层建筑的横风向风荷载与响应可能会进一步增大[2]。
自从Saunderst等[3]建议采用干扰状态下的变量与孤立状态下的变量之比分析周边建筑的干扰效应以来,Bailey等[4-7]大多将高层建筑风致响应的干扰因子(interference factor,IF)定义为相同折算风速下,有干扰和无干扰两种工况下目标建筑的响应之比。但对于结构风致响应而言,每个不同的折算风速下都可以计算出一个响应干扰因子IF,这使得问题变得很复杂。为此,Xie等[8-9]提出采用包络响应干扰因子(envelope interference factor,EIF),即一定折算风速范围内的干扰因子IF的最大值来分析干扰效应。
高层建筑的风致响应干扰效应的风洞试验研究有两类途径:一类是基于气动弹性模型试验直接测得有干扰和无干扰情况下位移或加速度响应[10-15];另一类是基于刚性模型风洞试验测得的气动力和建筑的结构动力特性通过随机振动理论计算响应[16-21]。前者试验结果更可靠,可直接使用,但需要在多个风速下进行试验,试验量很大,试验模型的设计制造难度大。后者只需在一个风速下进行试验,试验量大大减小,模型设计制造过程也很简单,所以被多数研究者使用,但它忽略了气动弹性效应。气动弹性效应机理非常复杂,其激励力为自激力,在研究中一般将它分成气动刚度力、气动质量力和气动阻尼力。对于超高层建筑来说,通常前两者影响比较小可以忽略,气动阻尼力可以用气动阻尼比来分析。一般而言,孤立工况下来流风速小于涡激共振临界风速时气动阻尼比为正值,抑制横风向振动;来流风速大于涡激共振临界风速时为负值,放大横风向振动。但是加入干扰建筑后,气动阻尼比的变化将更加复杂。基于刚性模型试验研究得到的干扰因子(忽略了气动阻尼比的影响)是偏于保守还是偏于危险,目前针对这个问题的探讨仍然比较少。黄鹏等[22]指出忽略气动弹性效应的影响可能大大低估邻近建筑对目标建筑的动力干扰因子,应得到系统深入的研究。
本文基于方形截面超高层建筑的一系列气动弹性模型测振风洞试验和刚性模型高频天平测力的风洞试验,得到有无干扰情况下的横风向风致加速度响应和气动力,分析了气动弹性效应对不同折算风速(或风速范围)干扰因子和包络干扰因子的影响,并结合典型工况下气动阻尼比随折减风速变化的情况进行了讨论,给出参考数据与建议。
1 试验概况
本研究的建筑缩尺前后几何尺寸及动力特性参数,如表1所示。其气动弹性模型如图1所示。模型上部结构由刚性芯棒,配重和外衣构成,可调节模型的外形和质量,位于风洞底板以上。下部结构由弹簧和阻尼板等构成,在风洞底板以下,可调节模型的刚度和结构阻尼比。整个模型结构可绕轴心在风洞地板高度处的万向架在3个方向上转动。本次试验中顺风向平动和扭转2个自由度被锁死,使得上部建筑模型只能沿着横风向进行振动。
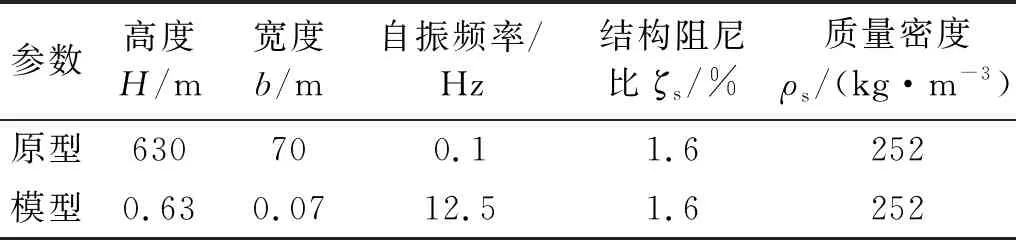
表1 建筑几何尺寸及动力特性参数
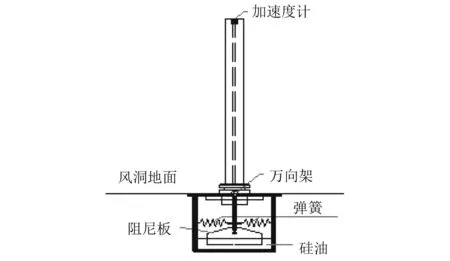
图1 气弹模型示意图
干扰建筑是和目标相同尺寸的固定不动的方柱。干扰建筑模型位置的网格如图2所示。总共有51个干扰位置。在气动弹性模型试验期间,每个干扰位置都会测量15个不同风速,使得目标建筑的折算风速(U*=UH/(f0b),UH为建筑顶部高度处的来流风速,f0为建筑模型基阶自由振动频率,b为建筑模型宽度)能够在3~14变化,涵盖了研究者所关心的涡激共振锁定区以及实际结构设计时工程师关心的折算风速范围。在高频天平测力试验时,使用了与气动弹性模型测振试验相同的模型尺寸、模拟风场和干扰条件。
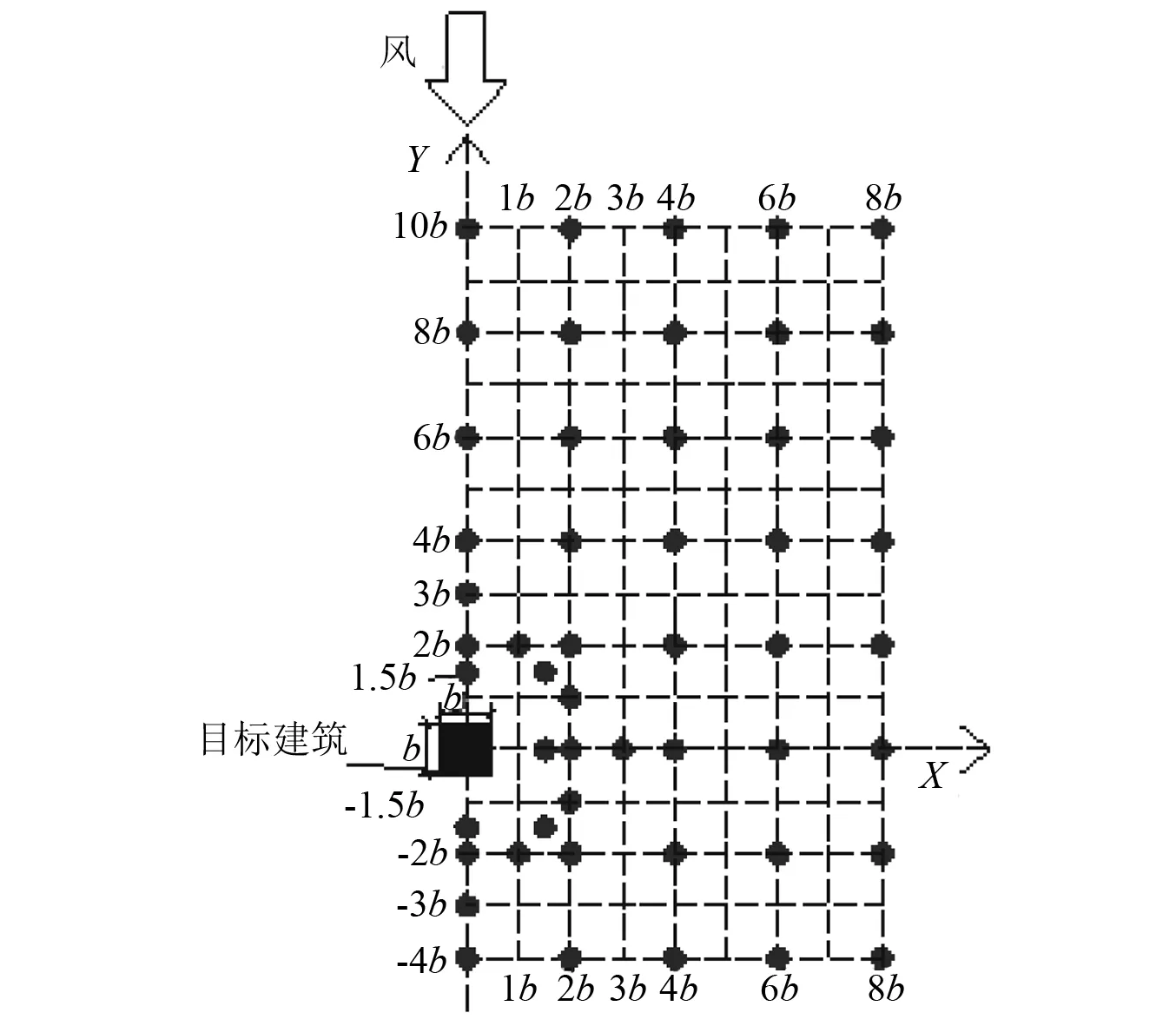
图2 干扰建筑位置坐标
本试验在同济大学TJ-1开口直流式风洞中完成。试验段风洞尺寸:宽×高×长=1.8 m×1.8 m×12 m。最大风速为30 m/s。试验模拟了较高湍流度的风场,对应模型顶部处的湍流度为9%。风场的参数如图3所示。模型顶部高度处的风速谱与Karman谱吻合良好。
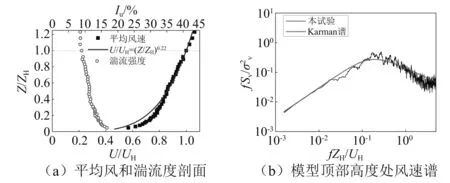
图3 模拟风场
2 试验结果
2.1 气动弹性模型试验结果
本文中气动弹性模型试验得到加速度响应的干扰因子IF和包络干扰因子EIF分别定义为
(1)
(2)
式中,σa0和σa分别为孤立状态和受扰状态下气动弹性模型顶部的加速度响应均方根值。
IF(U*)>1表示干扰建筑会放大目标建筑的响应,相反,IF(U*)<1表示干扰建筑会减小目标建筑的响应。为了便于分析,选取了3个具有代表性的风速来分析它们对应的干扰因子:孤立工况涡激共振前的低折算风速U*=6,孤立工况涡激共振临界风速U*=11,以及孤立工况跳出锁定区后的高折算风速U*=14,图4(a)~图4(c)分别给出在这三种情况下的IF等值线分布。图4(d)给出了试验风速范围(3≤U*≤14)内的包络干扰因子EIF的等值线图。
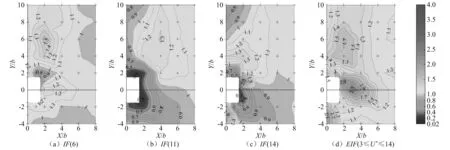
图4 干扰因子等值线云图及包络干扰因子云图
在低折算风速U*=6时,在上游(2,6)处有一个明显的IF峰值1.5,在其附近区域{X/b=1~3,Y/b=3~10},目标建筑受到干扰建筑的影响显著,其响应被放大了20%~50%。Bailey等的试验结果显示在位置(3,7)附近有一个IF峰值,本试验结果与它基本吻合。在并列干扰位置工况{X/b=2~4,Y/b=0}、正上游{X/b=0,Y/b=1.5~3}以及斜下游干扰位置{X/b=2,Y/b=-1~-2},其干扰因子IF也达到了1.2。但是在斜上游位置(1.5,1.5)附近,IF值在0.7~0.9,干扰工况下的响应被削弱。
在孤立工况涡激共振临界风速U*=11时,斜上游干扰位置工况的响应略有放大,干扰因子在1~1.3。其他干扰位置处,干扰因子IF均小于1.0,尤其是在{X/b=0~2,|Y/b|=0~3}的近距离干扰位置,响应减小了50%以上。
在高折算风速U*=14时,IF的分布规律与IF(11)和IF(6)很不相同。最大IF值高达2.3,出现在干扰位置(2,1)附近,随着干扰建筑远离该位置,IF值迅速减小。在(2,4)干扰位置附近,其IF也较大,最大值达到1.3。值得注意的是在目标建筑正下游位置{X/b=0,Y/b=-4~-1.5}, IF值远远大于1.0,最大IF值达1.9,这与直觉存在较大差异。在正上游{X/b=0~2,Y/b=1.5~3}和斜下游{X/b=1.5~6,Y/b=0~-4}出现了IF≤1.0的响应抑制区域,响应被抑制得最厉害的时候达70%。
Jungermannia ohbae Amkawa,Fl. 熊 源 新 等(2006);杨志平(2006)
对于包络干扰因子EIF,显然在整个试验干扰位置范围内其值都大于或等于1.0。其中在(2,6),(2,1),(3,0)和(0,-3)干扰位置附近,EIF分别有1.7,2.3,2.5和2.1的峰值,均存在响应被显著放大的折减风速工况。
2.2 气弹效应对干扰因子的影响
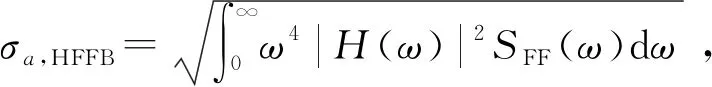
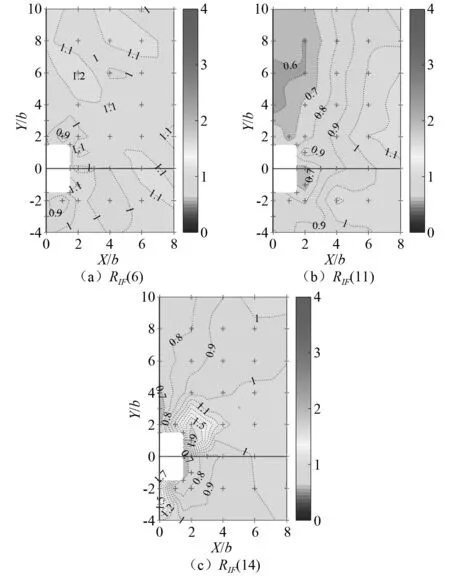
图5 不同折算风速下的RIF等值线分布
在低风速(U*=6)下,在上游干扰位置(2,6)附近RIF为1.2左右,即其气弹效应的影响达到20%,从图4中可知,该区域会使得目标建筑响应显著放大,最大IF达1.5,因此更加不可忽视。在其他干扰位置处,其RIF基本在0.9~1.1,即气动弹性效应对干扰因子的影响在10%范围内。这表明基于刚性模型试验研究得到的干扰因子在大部分低折减风速时基本与气弹试验干扰因子接近。
在孤立工况涡激共振临界折算风速(U*=11)时,RIF基本上小于等于1.0,尤其是在上游部分区域(比如(2,+6)和(0,+6))RIF达到0.6。气弹效应会使得干扰因子显著减小。这可能是由于孤立工况进入涡激共振,气弹效应显著放大了响应,但是在加入干扰后涡激共振可能被抑制,提前或延后发生,导致气弹效应并没有对显著放大目标建筑的响应。
对于高折算风速U*=14时,在斜上游(2,1)附近区域和正下游(0,-1.5)附近区域,RIF远大于1.0,忽略气弹效应会严重低估干扰因子IF的大小。RIF在这两个区域最大值分别达到了1.9和1.7。而这些干扰位置本身的干扰因子IF也是远大于1.0的(见图4(b)),因此其气动弹性效应不可忽视。在斜下游(1.5,-1.5)及附近区域,RIF在0.7~0.8左右,而该区域气弹试验的干扰因子IF本身小于1(见图4(c)),因此忽略气弹效应,会使得该区域的干扰因子偏于保守。
2.3 气弹效应对包络干扰因子的影响
为了分析气弹效应对包络干扰因子EIF的影响,定义了一个指标REIF
(3)
式中,EIF和EIFHFFT分别为基于气动弹性模型试验和刚性模型高平天平试验得到的包络影响因子,后者忽略了气动弹性效应。
对于刚性模型测压或高频天平试验计算的包络干扰因子,其折减风速范围通常设置为涡激共振临界折减风速以下,因此涡激共振临界折算风速前的包络干扰因子也是值得关注的。
图6(a)给出了折减风速10以下的包络干扰因子比REIF(3≤U*≤10)。绝大部分区域的REIF值都在0.9~1.1变动,即气动弹性效应对包络干扰因子的影响在10%范围内。但在斜下游(4,-3)附近区域,REIF值降低到0.8左右,也就是说忽略气动弹性效应将使该区域的包络干扰因子高估20%左右。
图6(b)给出了试验折算风速范围内的包络干扰因子比REIF(3≤U*≤14)。在斜上游(2,1.5)附近位置REIF达到1.7,在正下游(0,-1.5)~(0,-4)区域REIF达到1.5,忽略气动弹性效应将导致这些区域的包络干扰效应严重低估。正上游(0,3)~(0,7)区域的REIF值小于0.7,在斜上游(4,8)附近区域及斜下游(4,-3)附近区域REIF值在0.8左右,忽略气动弹性效应可能导致这些区域的干扰效应高估较多。
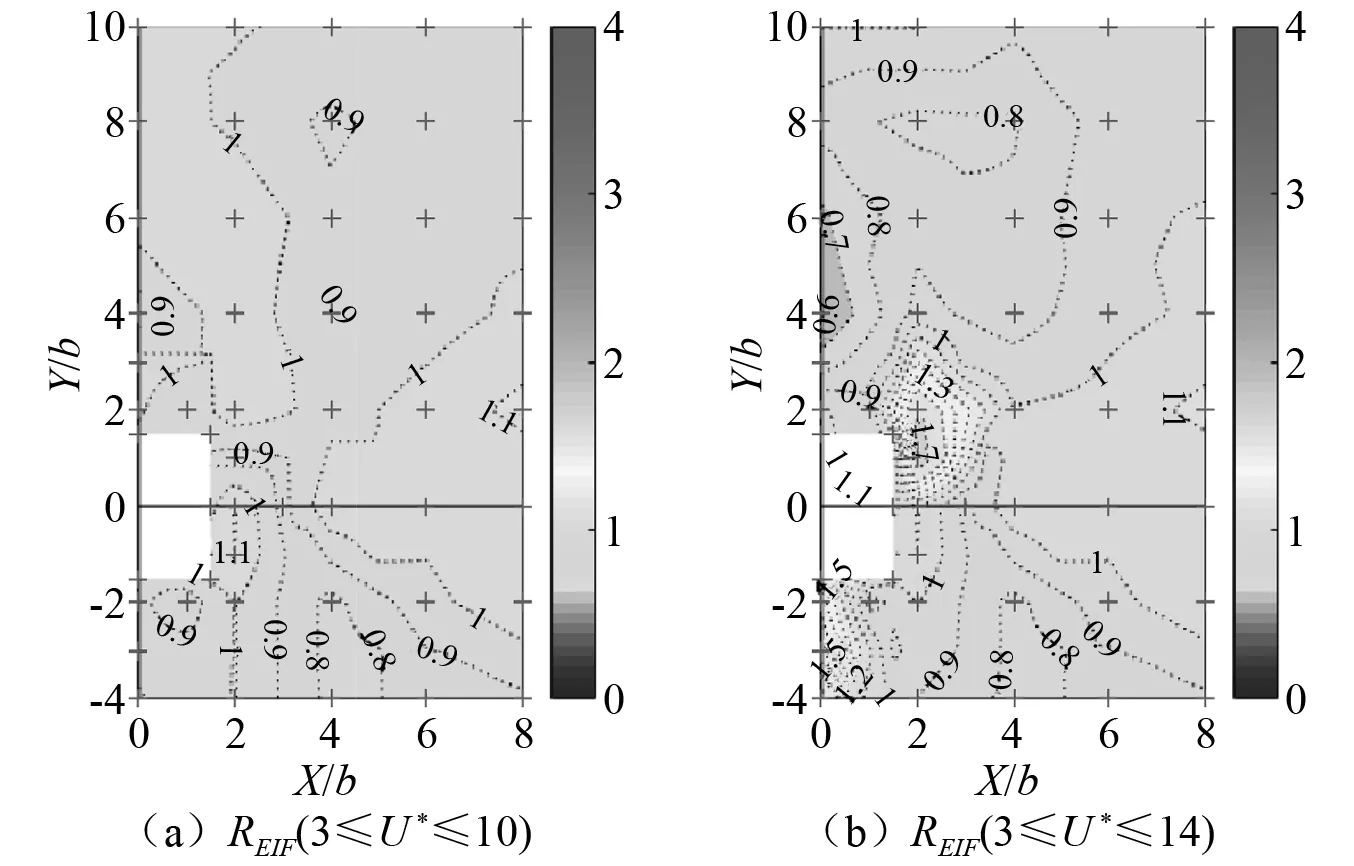
图6 不同折减风速范围的包络干扰因子比REIF等值线图
综上可知,在涡激共振临界折减风速前,忽略气弹效应的包络干扰因子EIF是基本可以适用的。而考虑更高折算风速时,在目标建筑{X/b=1.5~8,Y/b=0~4}区域,以及正下游{|X|/b=0~1,Y/b=-4~-1.5}区域,忽略气弹效应会严重低估真实的包络干扰因子EIF。
3 讨 论
由上文可知,气动弹性效应在上游(2, 6)以及下游(2,-1)干扰位置工况时对低折减风速的干扰因子的影响不可忽视。在斜上游(2,1)以及正下游(0,-1.5)附近区域,气弹效应使得高折减风速下的干扰因子以及包络干扰因子进一步放大。图7给出了这几个干扰工况下的气动弹性模型试验测得的加速度响应均方根值σa,基于HFFB试验研究得到的σa,HFFB以及考虑气动阻尼比的HFFB计算结果σa,HFFB+ζa随折减风速变化的情况。图8给出了典型工况下气动阻尼比ζa随折减风速变化的曲线。气动阻尼比通过气动力谱和假定传递函数拟合气弹模型加速度响应谱得到。
显然,考虑气动阻尼后,基于与HFFB计算的结果与气弹试验结果非常吻合。验证了气动阻尼比的准确性。对于孤立工况,在折算风速U*<10时,σa,HFFB大于气弹试验的结果σa(见图7)。此时目标建筑的气动阻尼ζa为正值(见图8),起到削弱横风向风致响应的作用;而在高折减风速(U*>11)下,σa,HFFB却小于振动模型试验的结果,因为此时目标建筑出现了负的气动阻尼,导致响应加剧。
在受到临近建筑干扰时,目标建筑的响应以及气动阻尼的变化情况比孤立状态下更加复杂。在上游(2,6)干扰工况下,当U*<12时σa,HFFB大于气弹试验结果,但是在U*>12时σa,HFFB基本与气弹试验结果没有差别。从图8的气动阻尼比变化来看,在U*<12时,气动阻尼比几乎都大于0,但是在U*<8时,其气动阻尼低于孤立工况对应的值,尤其是在U*=6时,气动阻尼比更是降低到0,比孤立工况ζa小了0.01,这也解释了干扰因子IF(见图4(a))及干扰因子比RIF(见图5(a))在该折减风速(U*=6)时出现的峰值。在下游干扰位置(2,-1)工况下,目标建筑的响应远小于孤立工况的,但是在U*<10时,其气动阻尼比非常接近0,小于孤立工况下对应的气动阻尼比。这导致了低折减风速的气弹效应对干扰因子的放大(见图5(a))。在U*>12时,其气动阻尼比仍然在+0.01附近波动,远大于孤立工况的负气动阻尼,这导致在高折减风速时其RIF<1.0(见图5(b))。气弹效应的存在使得目标建筑的横风向响应进一步被削弱,这也与图7的结果相吻合。
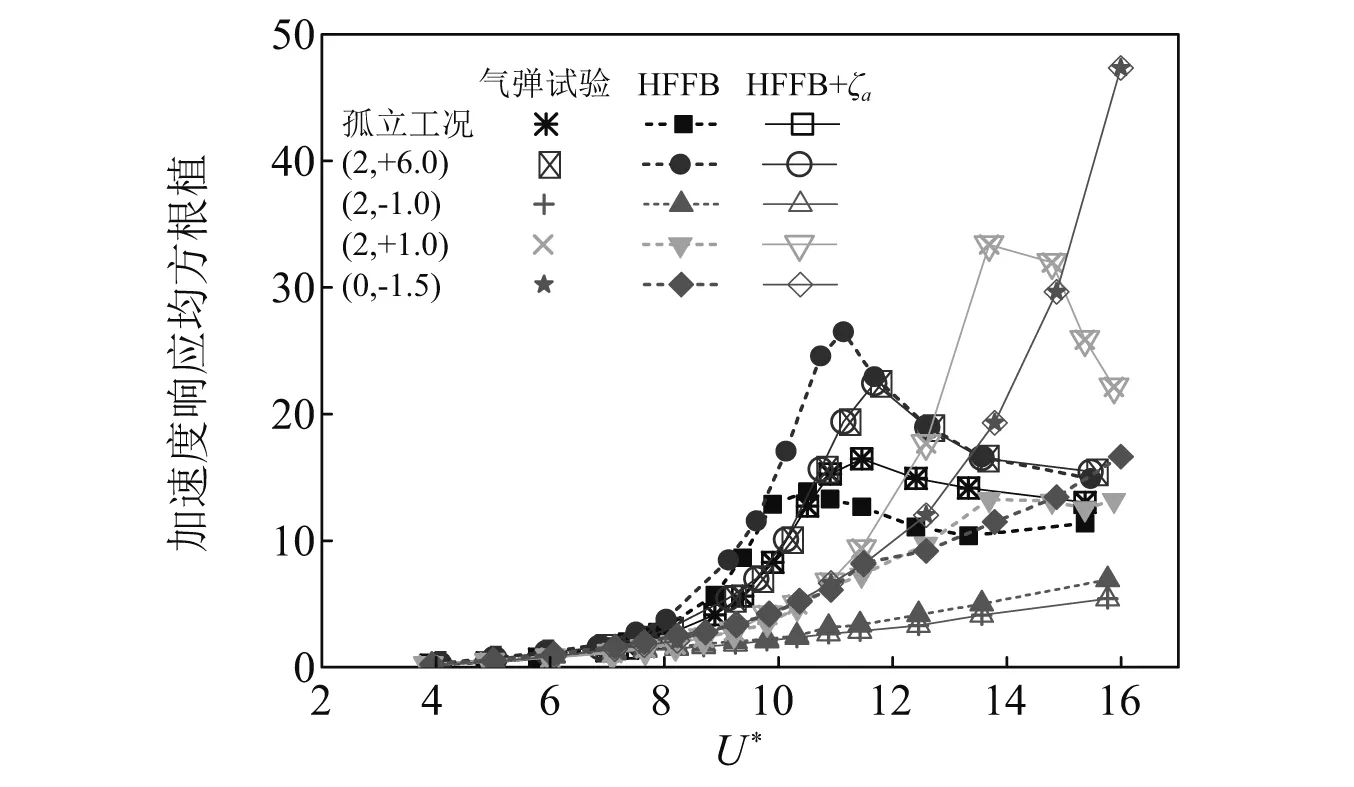
图7 典型工况下加速度响应均方根值对比
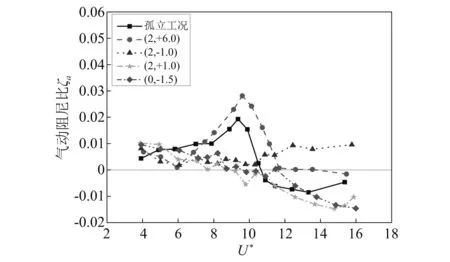
图8 典型工况下气动阻尼比随折减风速变化
在斜上游(2,1)以及正下游(0,-1.5)干扰位置工况下,目标建筑的气动阻尼比几乎随着折减风速的增大呈线性减小,在U*>13后,其负气动阻尼比已经低于对应孤立工况。气动弹性效应使得这些干扰工况下,目标建筑的响应在高折减风速下被显著放大。这也解释了图5(b)中该区域的高干扰因子比RIF和图6(b)中的高包络干扰因子比REIF。
4 结 论
通过方形截面超高层建筑的一系列气动弹性模型测振风洞试验和刚性模型高频天平测力风洞试验,本文分析了气弹效应对两个相同高层建筑间横风向风致响应的干扰因子和包络干扰因子的影响,结果表明:
(1) 在斜上游干扰位置(2,1)以及正下游干扰位置(0,-1.5)附近,目标建筑在高折减风速下产生了绝对值极大的负气动阻尼,该负气动阻尼显著放大了目标建筑的横风向风致响应,导致了高干扰因子IF和高包络干扰因子EIF。忽略目标建筑的气弹效应会使得设计偏于危险。
(2) 在涡激共振临界折减风速前,忽略气弹效应的包络干扰因子EIF基本上偏于保守,可以用于工程应用。
(3) 在(2,6)干扰位置处,在低折减风速时,由于其气动阻尼比较小,气弹效应放大了其干扰因子,该折减风速在实际工程中也比较常见,应该予以足够的重视。
(4) 在斜下游(2,-1)及附近区域,在高折减风速时目标建筑仍然保持正的气动阻尼,使得忽略气弹效应会使得该区域的干扰因子偏于保守。

