基于圆周割线改进型粒子群优化算法的叶片临界颤振辨识方法研究
李迺璐, 尹佳敏, 杨 华, 朱卫军
(扬州大学 电气与能源动力工程学院,江苏 扬州 225127)
风力机叶片在气动弹性耦合作用下易发生颤振问题[1],当来流风速达到颤振速度时会产生等幅振荡的临界稳定状态,即临界颤振[2-3]。
叶片临界颤振振动可描述一大类临界稳定的振动现象。对临界颤振系统辨识的研究,是利用其描述并研究高频、等幅振动特性,由此监测评估叶片的疲劳损伤,并为振动控制设计与研究提供模型。
叶片颤振系统本质为气弹系统,已有气弹系统的辨识研究主要集中在航空飞行器气弹系统的辨识,包括非线性状态空间辨识方法[4]、神经网络辨识方法[5]、ARMA自回归模型[6]和Hammerstein模型[7]等。这些方法主要针对飞行器气弹系统进行降阶辨识和非线性辨识,但是飞行器主要工作在高风速、超音速等工况下,而风力机叶片长期工作在低风速下,一般最高不超过25 m/s,因此,这些辨识方法并不能直接适用于风力机叶片颤振系统。
目前,叶片振动系统的辨识方法有最小二乘法[8-9]、双参数法[10]和自回归法[11]等,并获取了良好的辨识精度。然而,这些方法主要针对具有收敛稳定性的振动系统,还存在实际应用困难、受传感器安装角限制等问题。近年,智能优化算法,如差分进化算法被应用到风力机叶片衰减振动系统的参数辨识[12],进步提高了传统最小二乘法的辨识效果,具有辨识精度高、应用性好等优点。但智能算法本身的优化性能和针对问题的适应性,将直接影响辨识结果。在算法策略、优化效率和适用性上还有进一步提高的空间。
粒子群优化(partical swarm optimization, PSO)算法是一种模拟鸟群觅食行为、基于群体协作的搜索方法,具有易于实现、精度高和收敛快等特点[13],被广泛应用于系统辨识、函数优化等领域[14-15]。但PSO算法容易陷入局部最优,导致计算结果与全局最优值存在一定误差。为了提高粒子群优化性能,王峰等[16]将粒子群优化算法与凹函数权值递减策略相结合,并通过试验验证了改进粒子群优化算法的有效性。而基于改进型动态学习因子的粒子群优化算法(如改进型粒子群优化(modified particle swarm optimization,MPSO)算法、基于线性递减惯性权重的粒子群优化(linearly decreasing inertia weight based particle swarm optimization,LDIW-PSO)算法、基于动态学习因子的免疫粒子群优化(immune particle swarm optimization based on dynamically changing learning factors,IPSODCLF)算法)也被进一步提出并应用于典型函数的极值求解[17-18],风光水发电系统调度优化[19]和Volterra模型辨识[20]等,相比传统粒子群优化算法进一步提高了优化精度,并改善了陷入局部最优的问题。目前,针对叶片临界稳定振动系统的辨识方法研究还较少,值得进一步探索和研究。
本文把粒子群优化算法引入叶片临界颤振系统的辨识中,且为了提高算法的寻优能力、辨识效率和稳定性,创新设计了一种全新的改进型粒子群优化算法:圆周割线改进型粒子群优化(circular secant modified partical swarm optimization,CSM-PSO)算法。本文在CSM-PSO算法设计中,首次引入了几何圆周割线的距离来自适应调节学习因子,利用圆周角速度来控制调节速率,采用学习因子的均方和不变策略,有效增强了全局搜索和局部搜索的动态平衡,避免了优化过程中概率性偏重全局搜索或陷入局部最优,还提高了算法的优化效率和稳定性。将CSM-PSO算法应用于一个典型的叶片临界颤振系统的辨识仿真试验,对比多种改进型粒子群优化算法的辨识结果,验证了本文辨识方法在辨识精度、计算时间和鲁棒性方面的优越性。
该研究所设计的辨识方法,对了解风力机叶片、直升机叶片和机翼等系统的临界稳定振动特性、极限环振频和振幅分析,以及振动控制、避免耦合结构共振具有实际意义。
1 圆周割线粒子群优化算法
1.1 标准粒子群优化算法
粒子群优化算法是Kennedy等根据对鸟群捕食行为提出的一种寻优算法。每次迭代过程中,第i个粒子首先找到自己的历史最优解,即局部极值pi,j,进而所有粒子依次比较当代的最优值,找到当前的全局极值pg,j。局部极值和全局极值都遵从适应度值更小来更新粒子速度和位置,随着迭代次数全局最优解靠近。
粒子速度和位置更新的公式为
vi,j(k+1)=ω·vi,j(k)+c1r1·[pi,j-xi,j(k)]+c2r2·[pg,j-xi,j(k)]
(1)
xi,j(k+1)=xi,j(k)+vi,j(k+1),j=1,2,3,…,D
(2)
式中:vi,j为粒子速度;xi,j为粒子位置;ω为线性递减的惯性权重,表征粒子继承速度的能力;c1为局部学习因子,表征粒子向自身局部极值学习的能力;c2为全局学习因子,表征粒子向全局极值学习的能力;r1,r2分别为两个[0, 1]内的随机数。
粒子群优化算法中,种群规模、迭代次数、惯性权重、学习因子等参数都会对寻优结果产生影响。其中,学习因子选取不当将严重影响算法的寻优性能。不适合的c1使粒子缺少向自身历史轨迹学习的能力,只能向种群最优学习,种群会快速集中到一个最优解,但是在后期迭代中很难寻找更优的解,易陷入局部最优;不适合的c2使粒子缺乏向种群其他粒子学习的能力,粒子偏向单独行动,缺少相互交流,无法发挥种群寻优的优势,导致寻优速度慢且难以搜索全局最优解。
1.2 已有改进型粒子群优化算法
1.2.1 学习因子随权重变化的MPSO算法
MPSO算法通过递减的惯性权重来调节局部学习因子和全局学习因子,以增强粒子群优化算法进化时的统一性。MPSO算法采用异步变化的学习因子,公式为
c1MPSO=c1s-(c1s-c1e)cosω
c2MPSO=c2s+(c2e-c2s)cosω
(3)
式中:ω为非线性递减的惯性权重;c1s和c2s分别为局部学习因子c1MPSO和全局学习因子c2MPSO的起始值;c1e和c2e分别为局部学习因子和全局学习因子的终止值。在迭代初期,惯性权重和局部学习因子值较大,全局学习因子值较小,种群的全局寻优能力较强;在迭代后期,惯性权重和局部学习因子值较小,全局学习因子值较大,粒子更倾向于向种群中的全局最优学习,使算法更容易得到精确的解。该算法在五种典型测试函数的优化计算中取得更优结果。
1.2.2 学习因子随迭代次数变化的LDIW-PSO算法
LDIW-PSO算法为了改善传统粒子群优化算法的早熟收敛问题,利用阶段搜索的思想,基于迭代次数自适应调节学习因子。局部学习因子c1LPSO和全局学习因子c2LPSO随迭代次数的变化公式为
(4)
式中:k为当前迭代次数; iter max为最大迭代次数。当1≤k<0.47iter max时,c1LPSO>c2LPSO,局部学习因子较大,粒子更多的向个体历史最优学习,算法的全局寻优能力较强;当0.47iter max
1.2.3 免疫粒子群优化算法
针对目前粒子群优化算法中存在的易早熟、后期收敛速度慢等问题,免疫粒子群优化算法提出了一种动态调整学习因子的策略。
学习因子的更新公式为
c1CPSO=c1max-k(c1max-c1min)/kiter
c2CPSO=c2min+k(c2max-c2min)/kiter
(5)
式中:k为当前迭代次数;kiter为最大迭代次数;c1max,c2max分别为局部学习因子c1CPSO和全局学习因子c2CPSO的最大值;c1min,c2min分别为局部学习因子和全局学习因子的最小值。通过设置不同的c1max,c2max,c1min,c2min,可以实现学习因子的非对称性变化,使粒子早期尽快搜索到较优值,后期提高搜索精度,避免算法陷入局部最优。该算法利用到风光水联合系统优化调度模型的仿真计算中得到了改善的调度结果。
1.3 设计圆周割线改进型粒子群优化算法
由于粒子群优化算法在叶片振动系统辨识问题中的应用较少,如何选取合适的学习因子是提高叶片临界颤振系统辨识性能的关键,而已有改进型粒子群优化算法并非针对本文问题而设计。因此,针对叶片临界颤振辨识问题,本文首次设计了一种基于圆周割线型学习因子的新型粒子群优化(CSM-PSO)算法。
CSM-PSO算法的核心思路是将几何圆周割线引入粒子群优化算法学习因子的动态调节。主要体现在两个方面:①圆周上的点逆时针绕圆心移动的角速度,定义为学习因子的调节速率;②圆周上移动的点到水平线上固定点的割线距离,定义为学习因子的调节数值。
在学习因子的动态调节设计中,假设目标函数值会在某处大幅降低,将此处作为优化过程中的一个“分水岭”,即学习因子c1和c2动态调节的交叉点,算法在交叉点之前侧重c1,发挥粒子自身的寻优能力;在交叉点之后偏重c2,突出种群的寻优能力。基于圆周割线的学习因子动态调节原理,如图1所示。在水平线上取两个固定点使得OA=OB,将线段MA长度作为局部学习因子c1的取值,线段MB长度作为全局学习因子c2的取值,圆心角θ的对应点M沿圆周逆时针方向运动。随着θ从0°~180°变化,c1逐渐减小,c2逐渐增大,θ=90°时c1=c2,为动态调节中全局寻优和局部寻优的“分水岭”。
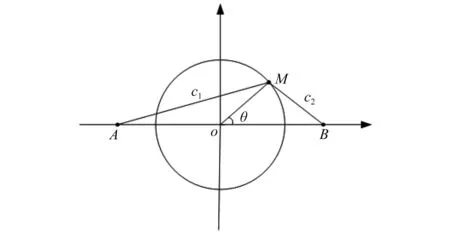
图1 基于圆周割线的学习因子动态调节原理图
圆心角θ的变化决定学习因子的动态调节速率,可表示为
θ=a×t+b×t2
(6)
式中:a,b为系数;t为当前迭代次数k与最大迭代次数G的比值,t=k/G。设当t=t*时为全局寻优和局部寻优的“分水岭”,则存在:①当t=0时,θ=0°,c1=cmax,c2=cmin;②当t=t*时,θ=90°,c1=c2;③当t=1时,θ=180°,c1=cmin,c2=cmax。
基于上述设计思想,基于圆周割线的学习因子公式为
(7)
式中,cmax,cmin分别为c1和c2取值范围的最大值和最小值。当k/G 从理论层面,所设计CSM-PSO算法的优点体现在以下几个方面: (1) 采用基于圆周角度的非线性调节速率,进一步增加了学习因子调节的平滑性,利于实现全局搜索和局部搜索的动态平衡; (2) 基于圆周割线的动态调节策略,从原理上使得局部学习因子和全局因子具有均方总和不变性,不同于已有方法的总和不变性,利于提高算法的鲁棒性; (3) 二维学习因子(c1,c2)的调节范围为正方形,克服已有方法的调节范围通常为随机长方形,避免概率性过度偏重全局寻优或局部寻优。 风力机叶片翼型的经典颤振模型可表示为 (8) (9) 式中:h为挥舞位移;θ为扭转角;mT为翼型质量;xα为质心和弹性轴之间的无量纲距离;b为半弦长;Iα为弹性轴转动惯量;ch和cα为阻尼系数;kh和kα为结构刚度;L和M分别为气动升力和气动力矩;U为风速;ρ空气密度;clθ,cmθ分别为攻角的气动升力系数和气动力矩系数;clβ,cmβ分别为尾缘襟翼的气动升力系数和气动力矩系数;β为尾缘襟翼角。 (10) 式中: 系统输出y为扭转角; 系统控制量u为尾缘襟翼角; 系统矩阵A,B,C和D分别为 C=[I2×202×2],D=[02×1]。 其中, 将状态空间方程式(10)转化为系统传递函数 (11) 式中,a1,a2,a3,b1,b2,b3,b4为叶片颤振系统参数,当式(9)中的风速U达到颤振风速U*时,式(11)达到叶片临界颤振状态。 对于叶片临界颤振系统辨识而言,目的是寻找一组式(11)的系统参数,使得系统输出与临界颤振输出响应的误差最小。 (12) 式中:ts为系统输出的采样时间;Nt为采样个数。寻优目的是最小化适应度函数值,从而获得最优的辨识结果。辨识算法具体流程为: 步骤1设置粒子群参数——粒子位置维度为7,设置种群规模S、迭代次数G等参数; 步骤2设置圆周割线参数——设置t*值并获取式(6)系数a,b的值,设置学习因子调节范围cmax,cmin; 步骤3初始化种群——随机初始化N个粒子的初始位置,令第i个粒子当前位置为个体最优位置pi(0),调用适应度函数,适应值最小的粒子位置为全局最优位置pg(0) 步骤4根据当前迭代次数k更新计算惯性权重ω (13) 步骤5基于圆周割线策略计算学习因子——根据式(7)计算全局学习因子c2和局部学习因子c1; 步骤6更新粒子位置和速度——根据式(1)和式(2),更新粒子的速度及位置,产生新种群; 步骤7更新个体最优——调用适应度函数,比较粒子的当前适应值J(Xi)和自身历史最优pi,如果J(Xi) 步骤8更新全局最优——比较粒子当前适应值J(Xi)与种群最优值pg,如果J(Xi) 步骤9重复步骤4~步骤8的,直到达到迭代要求,结束并输出最终结果。 基于CSM-PSO的叶片临界颤振系统辨识算法流程,如图2所示。 图2 基于CSM-PSO的叶片临界颤振辨识算法流程图 仿真试验以基于NACA0012翼型的叶片振动系统为研究对象,模型参数如表1所示。利用表1参数和软件MATLAB/Simluink进行颤振仿真试验,当风速增至9.6 m/s时,可观察到等幅振荡响应,如图3所示,即为临界颤振现象。因此,根据颤振速度U*=9.6 m/s和表1参数,可获取叶片临界颤振模型为 图3 叶片临界颤振响应 表1 基于NACA0012翼型的模型参数表 G(s)= (14) 将式(14)作为目标辨识模型,为四阶传递函数,包含7个待辨识的系统参数。临界颤振模型辨识的困难存在以下几个方面:①待辨识参数的量级差别较大,从101~104,不利于所有参数的精确辨识;②叶片临界颤振状态对应的系统参数具有唯一性,任意一个参数辨识误差较大,都无法正确辨识出临界颤振特性;③由于临界颤振为等幅振荡,本质上为临界稳定系统,该类系统普遍较难精确辨识。 利用本文设计的CSM-PSO算法对式(11)所示叶片临界颤振模型的参数进行辨识,种群规模为100,最大迭代次数为150,系统辨识的测试重复20次,结果取平均值。CSM-PSO算法的应用中,设t*=k/G=0.25,得到式(6)系数为a=7.330 4,b=-4.188 8,学习因子范围为cmax=2.5,cmin=0.2。 辨识试验主要从4个方面开展研究:①合适的辨识输入信号;②本文CSM-PSO算法的辨识精度;③CSM-PSO算法的辨识计算成本;④CSM-PSO辨识算法的鲁棒性。上述试验将与已有改进型粒子群优化算法的辨识结果进行对比研究。 3.3.1 输入信号 辨识要求持续激励的输入信号,本文分别采用白噪声、M序列作为辨识的输入信号进行试验。白噪声输入为[0,1]内的均匀白噪声信号,M序列输入为基于8个移位寄存器、幅值为1的M序列信号。 两种输入信号下的平均适应度函数进化曲线,如图4所示,白噪声输入信号下的进化曲线收敛慢,并存在较大辨识误差;而采用M序列输入信号可以获取较为精确的辨识结果。因此,传统白噪声输入信号并不适用于本文临界颤振辨识问题,而采用M序列时辨识误差更小、收敛速度更快,是本文临界颤振振动系统辨识比较合适的输入信号。 图4 不同输入信号下的Jave进化曲线 3.3.2 辨识精度 表2为M序列输入信号下,本文的CSM-PSO算法以及已有改进型粒子群优化算法(如MPSO, LDIW-PSO, IPSODCLF)所得到的临界颤振系统参数的辨识值、适应度函数平均值Jave和均方根Jsd,表2中真值来自式(14)系统参数。 表2 不同算法下的叶片临界颤振系统辨识结果 由表2可知,已有改进型粒子群优化算法获得的辨识误差较大,同时MPSO和LDIW-PSO算法辨识存在较大的均方根误差,说明针对临界颤振系统,已有先进粒子群优化算法难以实现精确、稳定的辨识。而本文所设计的CSM-PSO算法,在有限的种群规模和迭代次数下,辨识值更接近真值,其辨识精度明显较高、其辨识稳定性也显著优于其他算法。 图5给出了四种辨识方法分别得到的平均适应度函数的进化曲线。由图5中可知,CSM-PSO算法的收敛速度较快,并获取了较为满意的辨识精度;在有限迭代次数下,已有改进型粒子群优化算法收敛较慢,且难以搜寻全局最优值并陷入局部值。因此,相较下CSM-PSO算法明显改善了全局搜索能力、局部搜索能力和搜索过程中的动态平衡,在整个进化辨识中体现了较强的寻优性能、避免了陷入局部最优,实现了叶片临界颤振系统参数的高精度辨识。图6给出了辨识模型和真实模型的响应对比。 图5 不同算法的Jave进化曲线 图6 系统辨识响应对比 3.3.3 计算时间 表3给出了多种辨识算法的计算时间和适应度函数值。针对MPSO, LDIW-PSO和IPSODCLF辨识算法,设置种群S=100,迭代次数G=200,针对CSM-PSO算法设置S=100,G=100。 由表3可知,CSM-PSO算法在100次迭代下就可获得精确的辨识结果。在辨识时间方面,CSM-PSO算法明显降低了平均计算时间,表明了其优越的计算性能。对比表2结果,当迭代次数增加至200,MPSO, LDIW-PSO和IPSODCLF算法的平均适应度函数值有所改善,但是整体辨识误差依旧大于0.1。综上,已有改进型粒子群优化算法不仅花费的计算时间长,辨识效果也不佳。而本文所设计的CSM-PSO算法不仅辨识精度较高,还具有较低的计算成本。 表3 不同算法的辨识计算时间 3.3.4 鲁棒性 为了验证本文CSM-PSO算法的鲁棒性,对比多种已有算法,表4给出了20次运行,种群规模100和迭代次数150下的适应度函数值统计分析结果,包括最大值Jmax,最小值Jmin,平均值Jave、中间值Jmedi和均方差值Jsd。图7和图8分别给出了最大适应值和最小适应值的进化曲线。 由图7可知,辨识最差情况下,CSM-PSO算法仍可获取较高的辨识精度、较快的收敛速度,而其他算法均存在较大辨识误差。由图8可知,辨识最好情况下,CSM-PSO算法可在80次迭代后获取高精度的辨识结果,而其他三种算法此时未收敛或陷入局部最优值。 图7 不同算法的Jmax进化曲线 图8 不同算法的Jmin进化曲线 由表4可知, CSM-PSO算法的各方面统计结果,都显著优越于其他三种已有算法,特别是适应度函数的均方差值、最大值和最小值,说明CSM-PSO算法明显提高改善了算法的鲁棒性、稳定性和收敛性。 表4 不同算法的辨识鲁棒性分析 本文设计了圆周割线改进型粒子群优化算法,引入叶片临界颤振系统的参数辨识中,并在仿真试验中,将该辨识方法与基于MPSO,LDIW-PSO和IPSODCLF算法的辨识方法进行了对比分析。研究结果表明,与其他三种算法相比,提出的方法在辨识精度、计算时间和鲁棒性方面都具有显著的优越性。本文提出的方法,创新性地利用几何圆周割线来设计粒子群优化算法学习因子的动态调节策略,具有避免概率性偏重全局或局部寻优、利于全局搜索和局部搜索的动态平衡、算法稳定性强和寻优效率高的优点。本文设计的CSM-PSO算法及其在叶片临界颤振系统辨识中的应用,为临界稳定振动系统辨识提供了一种全新、高效、稳定的辨识方法,具有重要的理论价值和应用价值。2 叶片临界颤振系统辨识
2.1 叶片翼型振动模型
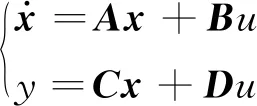
2.2 基于CSM-PSO的临界颤振辨识算法流程
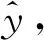
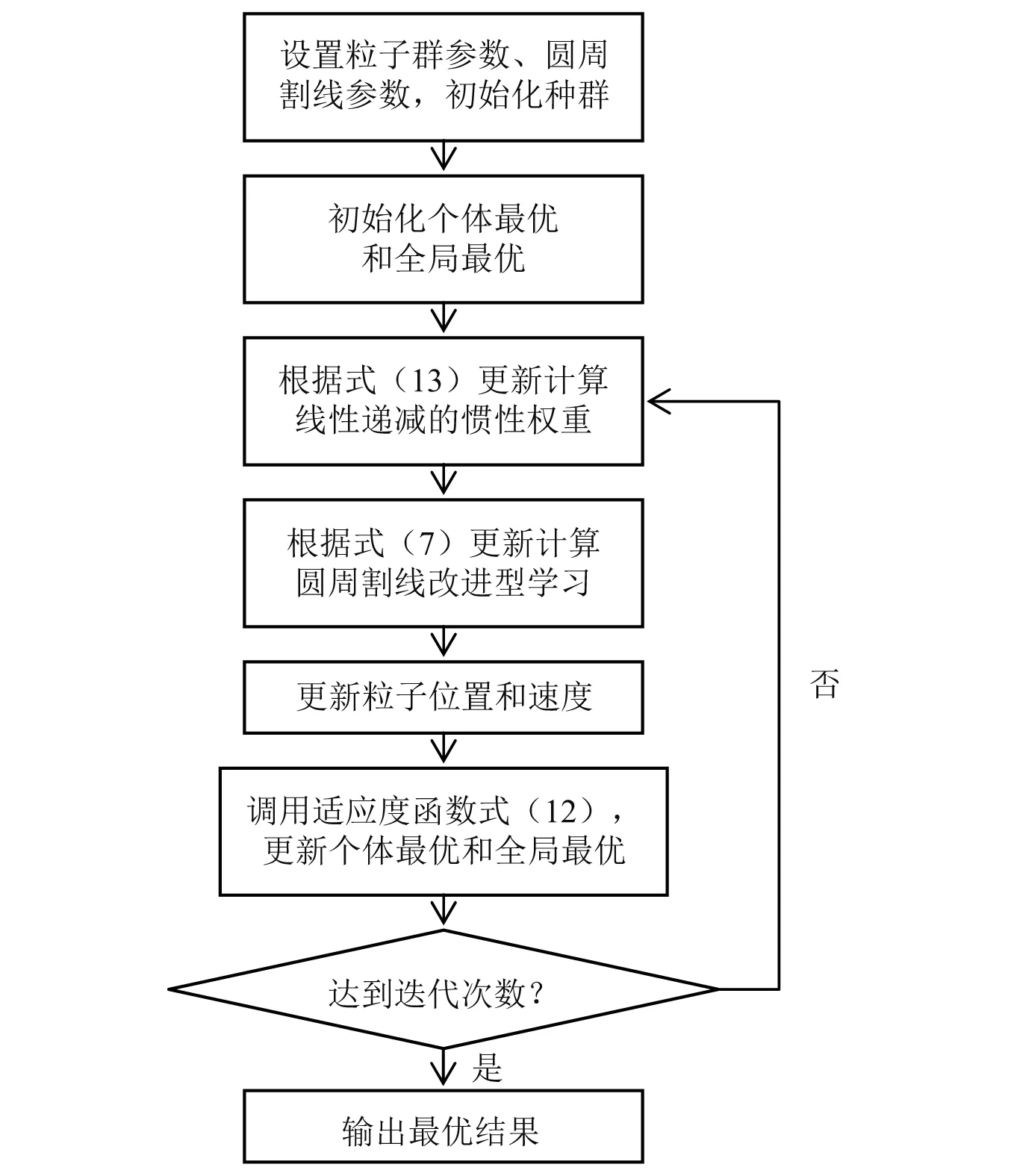
3 仿真研究
3.1 叶片临界颤振辨识问题

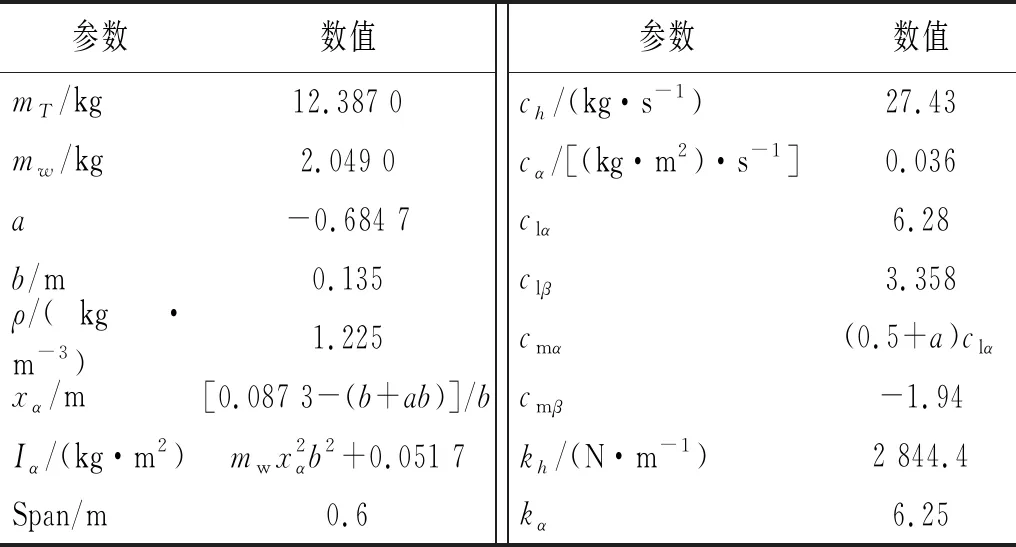

3.2 CSM-PSO算法的辨识应用
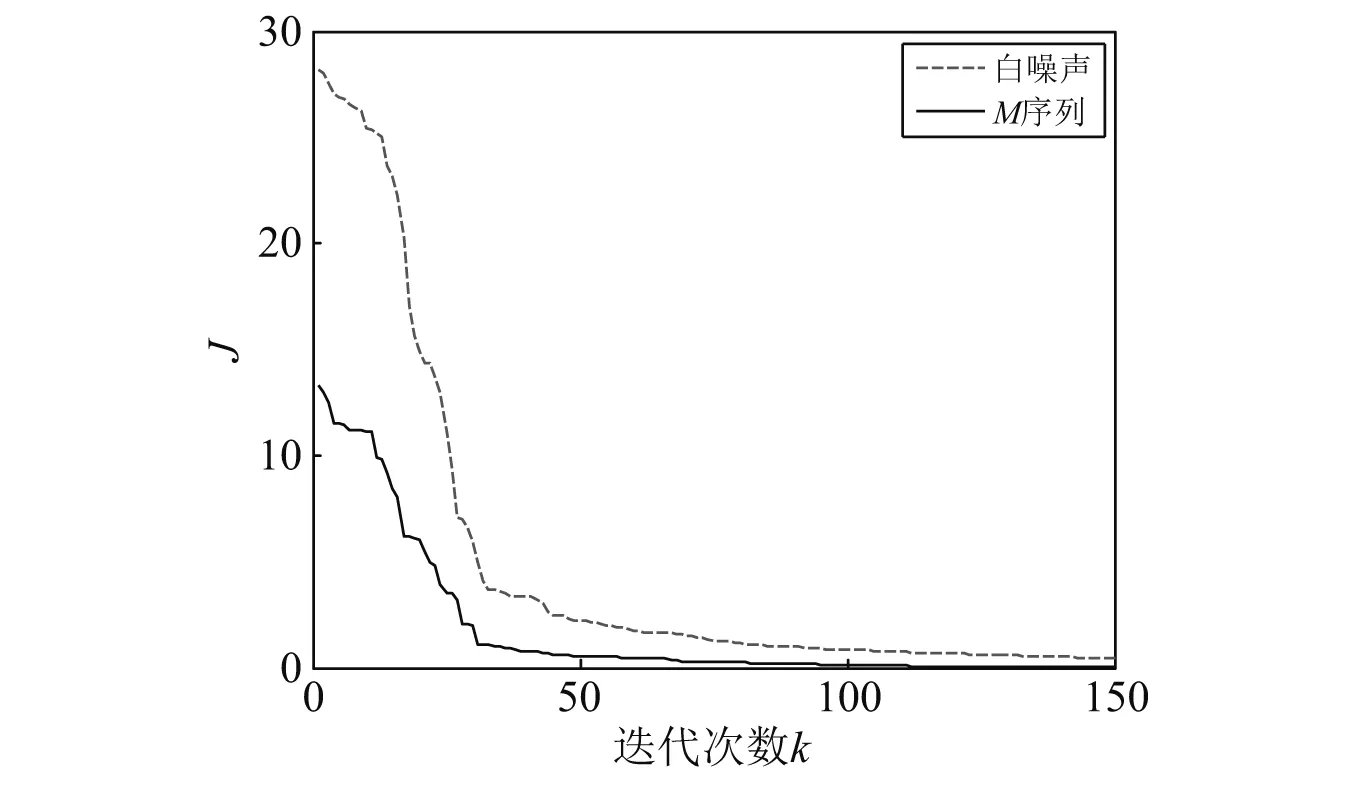
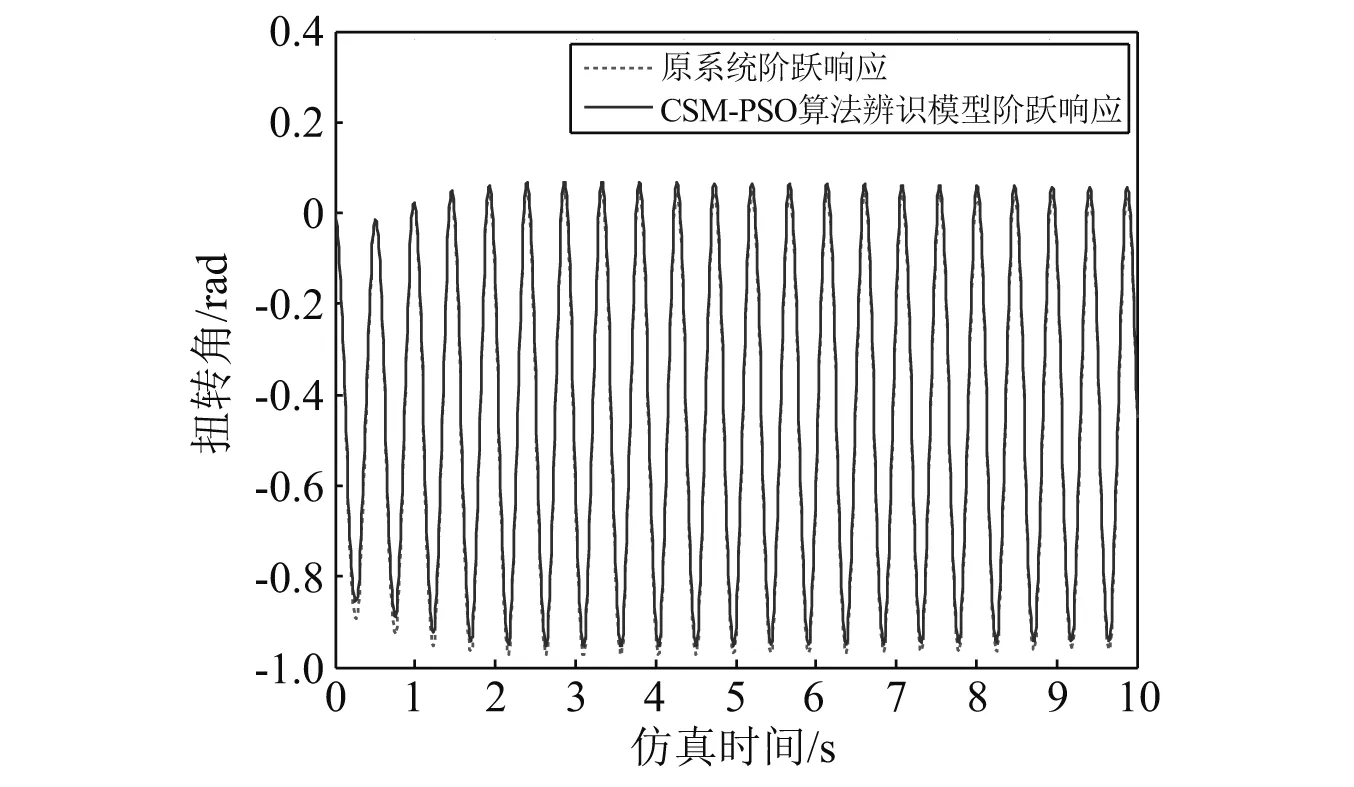
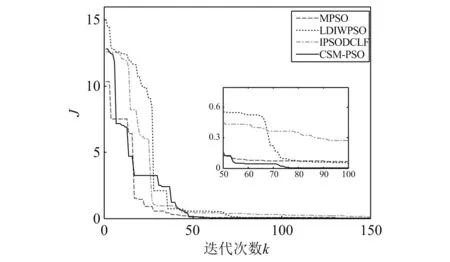
3.3 辨识结果





4 结 论

