双向地震激励下基于二维屈服面模型的残余位移谱研究

刘巴黎， 胡进军， 谢礼立

(1. 中国地震局 工程力学研究所，哈尔滨 150080；2. 中国地震局 地震工程与工程振动重点实验室，哈尔滨 150080)

震害表明，强震作用下工程结构因残余位移过大难以修复[1]。1985年墨西哥米却肯州地震和1995年日本神户地震，大量工程结构由于残余位移过大而不得不拆除[2-3]。残余位移由此受到国内外学者的关注，并逐渐被运用于结构抗震性能评估和地震损失评估[4-7]。FEMA P-58[8]将残余位移作为决定结构震后修复或拆除的重要指标。GB/T 38591—2020《建筑抗震韧性评价标准》[9]将结构残余层间变形作为建筑抗震韧性评价的重要指标，并规定了部分结构形式层残余位移角的限值。

近年来，国内外学者对残余位移进行了广泛的研究。Ruiz-Garcia等[10]对单自由度(single degree of freedom，SDOF)体系残余位移比谱进行了系统研究，构建了等强度残余位移比谱的拟合公式。Ji等[11]和Harikrishnan等[12]分别建立了SDOF体系等强度残余位移比谱。Harikrishnan等[13]对SDOF体系等延性残余位移比谱进行了进一步研究，研究了场地类别、震级、断层距和持时对等延性残余位移比谱的影响，提出了等延性残余位移比谱的经验公式。在国内，叶列平等[14]研究认为屈服后刚度对结构残余位移的较大。郝建兵等[15]和胡晓斌等[16]分别建立了等强度残余位移比谱的预测方程。张勤等[17]基于实际地震动记录，研究了SDOF体系模型和地震动不确定性对残余位移的影响，提出了残余位移的概率计算模型。黎璟等[18]提出了近断层脉冲型地震作用下结构残余位移设计谱。

地震动的多维性和结构非线性反应的空间耦合性使单向地震激励下的结构动力分析具有明显局限性[19]。文献[20]表明，多维地震激励下结构反应比单向地震激励下结构反应大得多。双向地震激励结构在一个主轴方向的损伤往往会影响其另一主轴方向动力响应特性[21-24]。王东升等[25]基于双向地震激励下的等强度折减系数谱分析结果，认为与单向地震激励下相比，双向地震激励下会增大结构周期较长方向的最大位移反应。王丰等[26]针对单向地震激励下能量反应谱的不足，提出双向地震激励下标准化的等延性系数地震输入能量反应谱，分析了场地类别、延性系数及周期比对标准化能量反应谱的影响，研究表明单自由度体系在单向地震激励下会高估结构的能量反应。目前所有残余位移谱的研究几乎都集中于单自由度体系和单向地震激励。地震动的多维性及其对结构作用的空间耦合性使得单向地震激励下结构残余位移分析具有局限性。为准确评估结构残余位移需求，需考虑多维地震激励下结构的弹塑性动力特性。在单向地震激励下残余位移谱理论的基础上建立双向地震激励下的残余位移谱模型，具有重要的理论意义和使用价值。

鉴于此，本文建立了恢复力特性符合二维屈服面模型的单质点双自由度体系(single-mass dual-degree of freedom，SMDDOF)，以此为基础推导出单质点双自由度体系在双向地震激励下的运动方程，进而提出单质点双自由度体系在双向地震激励下的残余位移谱模型，分析场地条件和两主轴方向刚度比对残余位移谱的影响，以期为残余位移的准确评估及抗震韧性评价提供参考。

1 单质点双自由度体系的运动方程

1.1 谱模型

双向地震激励下,单质点体系沿两个相互垂直的主轴方向(x方向和y方向)平动时的运动方程可以表示为

(1)

式中：m为系统的质量；cx和cy分别为系统沿两个主轴方向的阻尼系数；x(t)和y(t)分别为系统沿两个主轴方向的位移反应；f(x,t)和f(y,t)分别为系统沿两个主轴方向的恢复力；xg(t)和yg(t)分别为系统沿两个主轴方向的地面运动位移。系统沿两个主轴方向的强度折减系数为

(2)

式中：fx,y和fy,y为不考虑耦合影响的系统沿两个主轴方向的屈服力；fx,e和fy,e为系统沿两个主轴方向的弹性地震力。单质点双自由度体系在弹性状态下相当于两个独立的弹性单自由度体系，所以fx,e和fy,e可分别表示为

(3)

式中：βx和βy分别为系统沿两个主轴方向的放大系数谱。引入无量纲量μx，μy以及τx，τy，关系式如式(4)所示。由式(4)可知：μx，μy分别为系统沿两个主轴方向的延性系数；τx，τy分别为系统沿两个主轴方向的归一化加速度时程，反映地震动的频谱特性。

(4)

将上述定义的关系式(2)～式(4)代入式(1)中，有

(5)

式中：ωx和ωy为系统的圆频率；ξ为系统的阻尼比，本文取系统沿两个主轴方向的阻尼比ξx=ξy=0.05。从统计上来看，同一场地两正交方向的地震动强度和频谱特性是相似的。系统沿两个主轴方向的屈服强度比值可表示为fx,y/fy,y=α(ωx)/α(ωy)，其中，α为地震影响系数，由规范设计谱确定。所以，系统沿两个主轴方向的强度折减系数的关系可表示为

(6)

基于以上推导，可以建立单质点双自由度体系的弹塑性谱。式(5)建立了单质点双自由度体系强度折减系数R、延性系数μ以及周期T的关系，即：R-μ-T关系。

1.2 二维屈服面模型

假定单质点双自由度体系的恢复力特性符合二维屈服面模型[27]，可以表示为

(7)

式中，n为屈服面形状控制参数，反映了系统沿两个主轴方向恢复力的耦合效应。当n=2时，屈服面近似为椭圆；当n>10时，近似为矩形，即：系统沿两个主轴方向的恢复力近似于相互独立。n对屈服面形状的影响如图1所示。本文按照通常情况取n=2。同时为了简化分析，体系恢复力模型取理想弹塑性模型，则本文建立的单质点双自由度体系可描述为：沿两个相互垂直的主轴方向上分别具有水平平动自由度，恢复力特性符合二维屈服面模型的理想弹塑性单质点体系。体系的恢复力矩阵如式(8)所示。

图1 参数n对屈服面形状的影响

(8)

2 地震动记录的选取

本文从美国太平洋地震工程研究中心(PEER NGA-West2)强震数据库中挑选140组地震动记录，挑选原则简述如下：①仪器安放位置位于自由地表；②矩震级大于5.5；③所选地震动两个分量的峰值加速度(peak ground acceleration，PGA)均大于40 cm/s2；④所选记录不包含脉冲型地震动记录。将选取的地震动记录依照据NEHRP[28]规范的场地划分标准分为四类： AB类(A类和B类合为一类)、C类、D类及E类，每类场地各35组地震动记录。选取的地震动记录震级-断层距分布图，如图2所示。

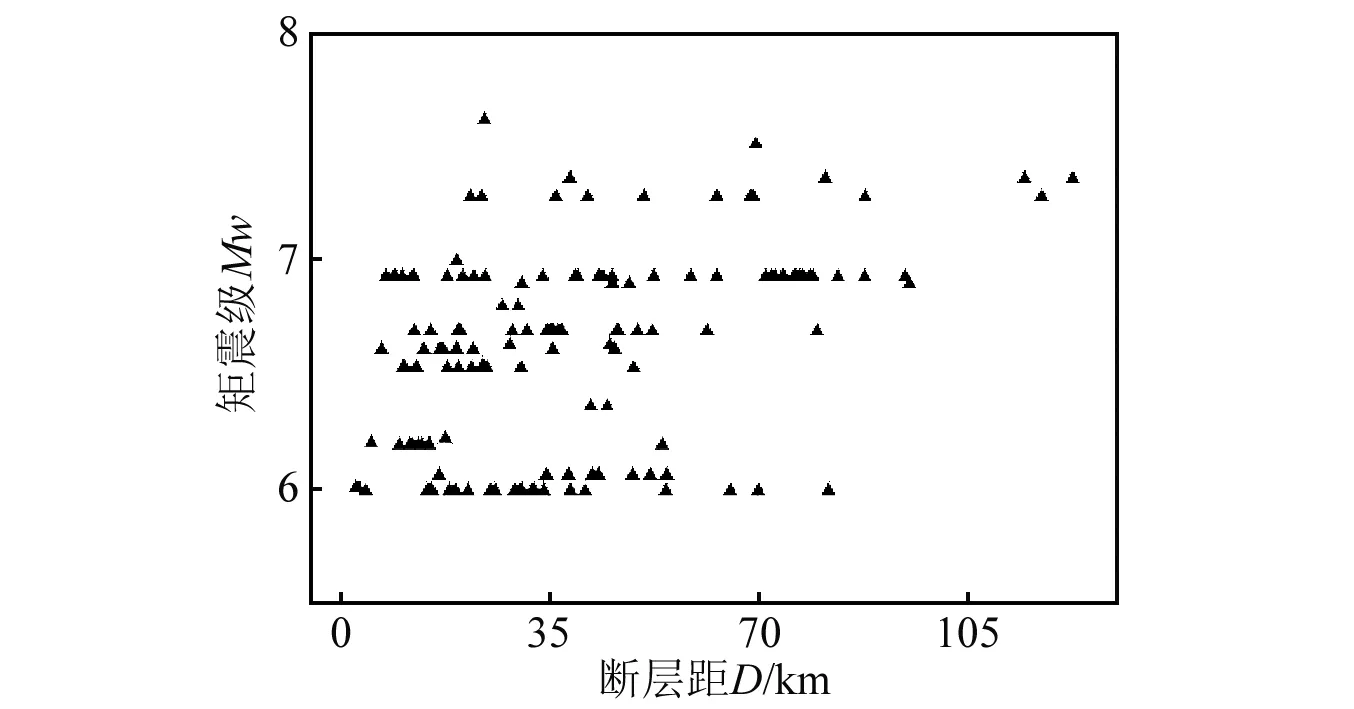
图2 震级-断层距分布图

3 单向地震激励下残余位移谱模型准确性验证

图3给出了AB类、C类和D类场地的单自由度体系单向地震激励下的等强度残余位移比谱Cres(残余位移与弹性谱位移的比值)以及Ruiz-Garcia等研究中的等强度残余位移比谱统计结果。可以看出：单自由度体系单向地震激励下的等强度残余位移比谱在整个周期段内可以分成两部分：在0～1.0 s周期内，残余位移比谱值随周期增大而减小；在1.0～3.0 s周期内，残余位移比谱值对周期的变化不敏感。此外，在整个周期范围内残余位移比谱随强度折减系数的增大而增大。本文的统计结果和Ruiz-Garcia等研究中的统计结果在整个周期段内差距较小，确保了本文建立的单自由度体系在单向地震激励下的残余位移谱模型的合理性。为准确评估结构残余位移需求，需考虑多维地震激励下结构的弹塑性动力特性。本文在单自由度体系单向地震激励下残余位移谱理论的基础上建立单质点双自由度体系双向地震激励下的残余位移谱模型。

图3 单向地震激励下残余位移谱

4 单向和双向地震激励下残余位移谱对比分析

为了研究多维地震激励下结构弹塑性动力特性耦合效应对残余位移的影响，本节对比分析了不同场地条件下单自由度体系单向和双向地震激励下残余位移谱。定义单质点双自由度体系在双向地震激励下沿x方向残余位移与单自由度体系单向地震激励下残余位移的比值为αres，图4给出了不同场地条件下的比值谱。由图4可知，不同场地条件下的αres值通常都大于1，且αres值受场地条件和周期的影响较小。这说明通过单自由度体系单向地震动输入建立的残余位移谱可能会低估结构的残余位移需求。

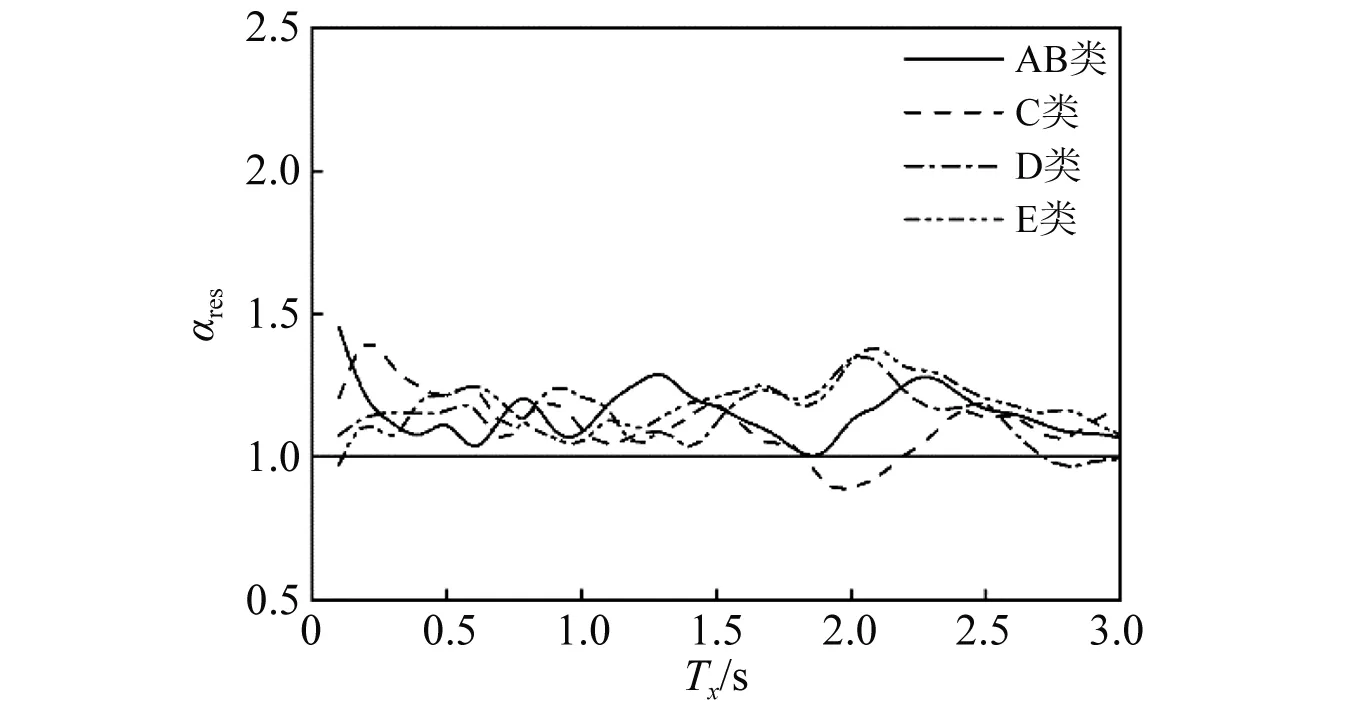
图4 双向和单向地震激励下残余位移谱比值(Rx=2)

5 双向地震激励下残余位移谱分析

5.1 分析变量

由建立的单质点双自由度体系运动方程可知，影响残余位移的因素有场地类别、两个主轴方向的自振周期(两主轴方向刚度比取ζ=ky/kx)及强度折减系数R或延性系数μ。既有结构的目标延性系数很难确定，等强度折减系数弹塑性谱显然更加合理[29]。本文主要研究双向地震激励下的等强度残余位移谱。

结构动力时程分析时一般将变形参数和其他重要参数进行归一化处理。常用的归一化参数有弹塑性谱位移、弹性谱位移及屈服位移。弹塑性谱位移和屈服位移为反映结构弹塑性特征的参数，需要通过弹塑性分析才能得到，而弹性谱位移只需计算位移反应谱便可获得。本文在研究双向地震激励下的残余位移响应规律时，采用弹性谱位移sde对残余位移进行归一化得到残余位移比Cres。

针对单质点双自由度体系进行非线性时程分析，采用Newmark-β法求解运动方程，建立等强度残余位移比谱。积分采用文献[30]建议的步长，即：地震动记录采样时间间隔，自振周期的1/25以及0.01 s三者的最小值。分析中考虑的变量如下：①x方向的强度折减系数Rx=2，3，4，5，6；②x方向的周期Tx取为0.1～3 s，周期间隔为0.1 s；③两主轴方向的刚度比ζ=ky/kx取0.25，1，4；④四类场地总共140组地震动记录，时程分析时每个地震动分量均需沿体系的x方向输入一次，相当于280组地震动记录。

5.2 场地条件的影响

图5给出了按不同场地条件分类强度折减系数Rx=2，4，6沿x方向的残余位移比谱。由图5(a)可知，Rx=2等强度残余位移比谱受场地条件的影响很小。由图5(b)和图5(c)可知，AB类、C类和D类场地的等强度残余位移比谱值受场地条件的影响较小，E类场地的残余位移比谱值大于其他三类场地的残余位移比谱值。值得注意的是，文献[31]针对单质点单自由度体系研究了场地条件对残余位移比谱的影响，研究表明：相比其他场地条件，软土场地下结构残余位移需求增大。综上所述，场地条件对双向地震激励下残余位移比谱有一定的影响，软土场地下结构残余位移的评估必须考虑场地条件的影响。

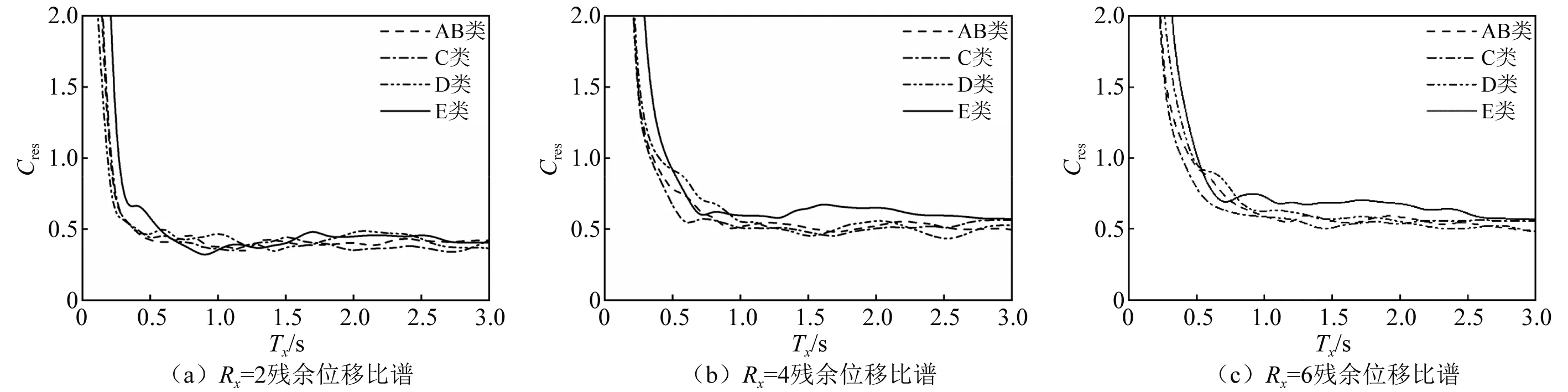
图5 场地条件对双向地震激励下残余位移比谱的影响

5.3 两主轴方向刚度比的影响

图6给出了四类场地不同刚度比下强度折减系数Rx=2，4，6沿x方向的残余位移比谱。由图6可知，双向地震激励下的等强度残余位移比谱在整个周期段内可以分成两部分：在0～1 s周期内，不同刚度比的残余位移比谱值随周期增大而减小，不同刚度比下的残余位移比谱值差距很小；在1～3 s周期内，不同刚度比的残余位移比谱值对周期的变化不敏感，残余位移比谱值随刚度比的增大而增大。1～3 s周期内：在Rx=2情况下，刚度比ky/kx=4与ky/kx=0.25残余位移谱值之比接近1.2；在Rx=4情况下，残余位移谱值之比接近1.3；在Rx=6情况下，残余位移谱值之比接近1.4。这说明强度折减系数对双向地震激励下的残余位移比谱有一定的影响。

图6 刚度比对双向地震激励下残余位移比谱的影响

为了进一步研究刚度比对残余位移响应的影响，图7给出了不同刚度比下沿x方向的残余位移谱ures,X(未归一化的残余位移)以及两主轴方向残余位移平方和开平方后的谱值ures,SRSS。由图7(a)可知，周期大于1 s时，ures,X随刚度比的增大而增大；由图7(b)可知，ures,SRSS受刚度比影响的规律正好与残余位移谱值相反，即：ures,SRSS随刚度比的增大而减小。这说明，在中长周期范围内随着x主轴方向刚度的削弱，会增大该主轴方向的残余位移需求，而另一主轴方向的残余位移需求会有所减小。

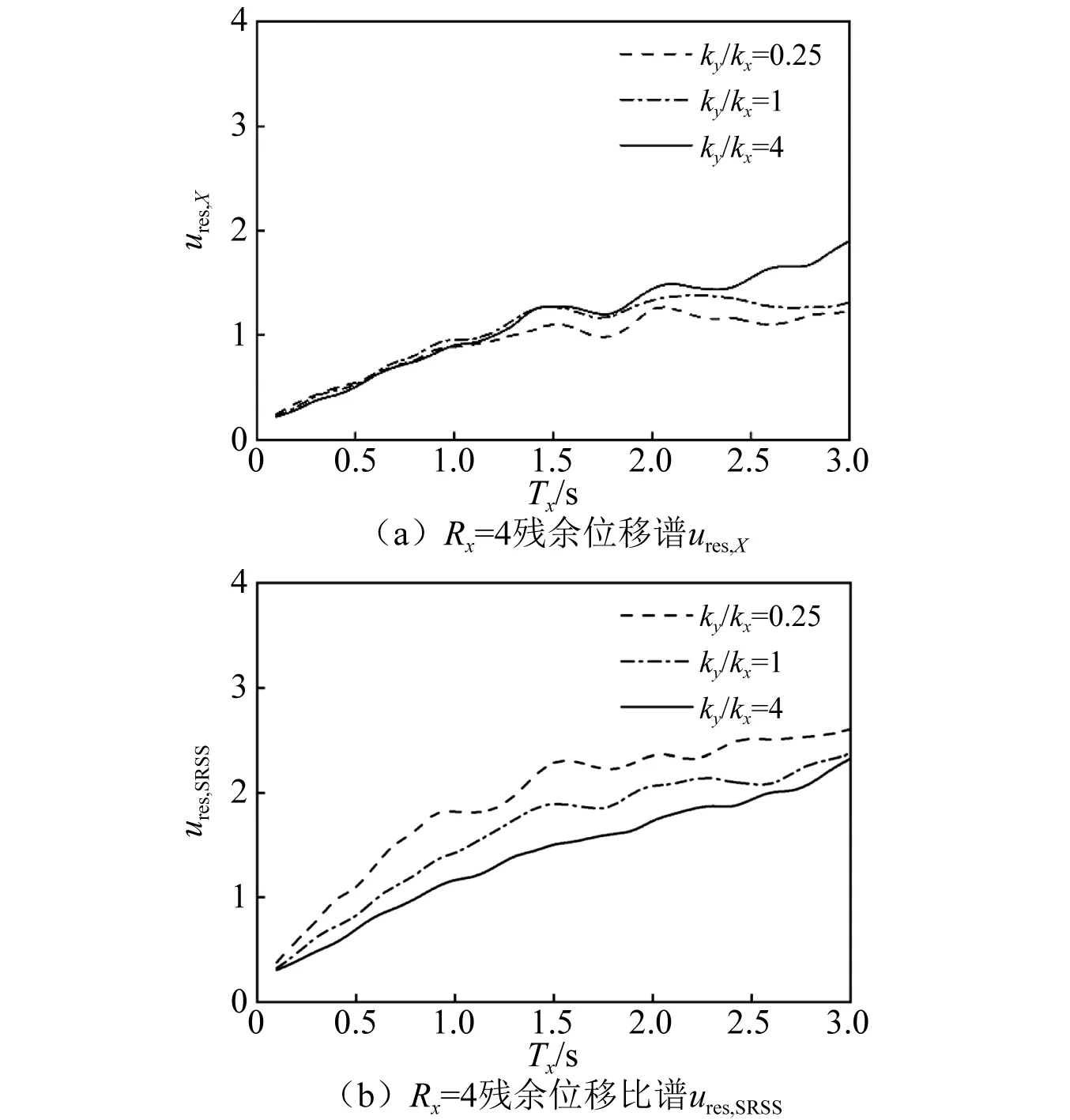
图7 刚度比对双向地震激励下残余位移谱的影响

x主轴方向刚度较小，结构在该方向很快屈服且损伤较为严重。与之垂直方向的刚度相对较大，结构在该方向损伤较x方向轻，结构损伤主要集中于x主轴方向。双向地震激励下结构弹塑性动力特性的耦合效应对位移响应的影响，取决于两主轴方向耗能及损伤的相互制约，这一点与宁超列等的结论一致。综上所述，恢复力耦合效应对结构残余位移响应的影响取决于两主轴方向损伤的相互制约。在中长周期范围内：某一主轴方向刚度的削弱会增大该主轴方向的残余位移需求；而另一主轴方向的残余位移需求会有所减小。

6 结 论

本文基于大量分类地震动记录建立统计平均谱，对比分析了不同场地条件下单向和双向地震激励下残余位移谱，同时分析了场地条件以及两主轴方向刚度比对残余位移谱的影响，得出以下结论：

(1) 通过单自由度体系单向地震动输入建立的残余位移谱可能会低估结构残余位移需求。

(2) 场地条件对双向地震激励下结构残余位移谱有一定的影响，结构残余位移需求的评估必须考虑软土的影响。

(3) 在0～1 s周期内，双向地震激励下两主轴刚度比对结构残余位移比谱的影响较小；在1～3 s周期内，双向地震激励下残余位移比谱值随两主轴刚度比的增大而增大。

(4) 恢复力耦合效应对结构残余位移响应的影响取决于两主轴方向损伤的相互制约。在中长周期范围内：某一主轴方向刚度的削弱会增大该主轴方向的残余位移需求；而另一主轴方向的残余位移需求会有所减小。

致谢

感谢美国太平洋地震工程研究中心(PEER)NGA计划项目提供的地震动数据。