考虑油沟的轴承边缘应力仿真分析和优化

李凌翔，杨新清，刘贇

(泛亚汽车技术中心有限公司，上海 201208)

1 概述

油沟(图1)是轴承的重要组成部分[1]，主要作用是储存润滑油并作为滚道磨削时的砂轮越程槽[2-8]。某变速箱轴承基于传统赫兹弹性接触理论校核无边缘应力(图2)，但实际使用中多次出现输出轴前端圆柱滚子轴承内圈滚道边缘首先发生剥落，进而向滚道面中心扩展(图3)。分析其主要原因为传统赫兹接触理论计算应力时忽略了油沟的影响，将接触长度按滚子有效长度设置，但当油沟沿滚道方向的宽度大于滚子倒角时，严重影响滚道边缘与滚子的接触状态，已不能忽略油沟的影响，故传统赫兹弹性接触理论并不能真实反映滚子与内外圈的实际接触情况。

图1 圆柱滚子轴承油沟示意图Fig.1 Diagram of oil groove of cylindrical roller bearing

图2 未考虑油沟时内圈应力Fig.2 Inner ring stress without considering oil groove

图3 输出轴前端轴承内圈边缘点蚀Fig.3 Edge pitting of front bearing inner ring of output shaft

鉴于此，以某变速箱用圆柱滚子轴承为例，基于赫兹接触理论，通过MASTA软件根据实际油沟尺寸对分析模型加以修正，实现轴承边缘应力的准确计算。

2 轴承系统模型的建立

以某变速箱CRB39/74圆柱滚子轴承为研究对象，其主要结构参数见表1，轴承额定动载荷Cr为67.18 kN，额定静载荷C0r为74.28 kN。

表1 轴承主要结构参数Tab.1 Main structural parameters of bearing

对数修形滚子中间圆弧半径大，两侧圆弧半径小，能有效解决轴承边缘应力。对数修形滚子素线方程为[9]

(1)

Lwe=Lw-2r，

式中：ν为滚子材料泊松比；E为滚子材料弹性模量；Qmax为滚子所受最大载荷；Fr为轴承所受径向载荷；对于滚子轴承，1/Jr取4.08；Lwe为滚子有效接触长度。

凸度近似值为

(2)

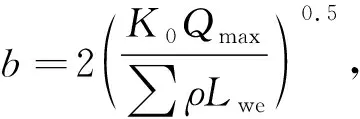
式中：K0为材料常数，对于普通轴承钢，取2.81×10-6mm2/N；b为滚子与滚道接触区半宽；∑ρ为滚子与滚道接触的综合曲率；Dpw为滚子组节圆直径；Dwe为滚子有效直径。

轴承内圈、外圈和滚子均修形，边缘应力发生在最小凸度(修形量有公差，最小凸度是修形量的下偏差)情况下，考虑制造公差，此时内、外圈最小全圆弧修形分别为0.004，0.003 mm，滚子最小对数修形为0.018 mm。

发动机最大输出扭矩为180 N·m, 变速箱速比见表2，变速箱在一挡载荷最大，一挡和主减速齿轮参数见表3。

表2 变速箱速比Tab.2 Transmission ratio

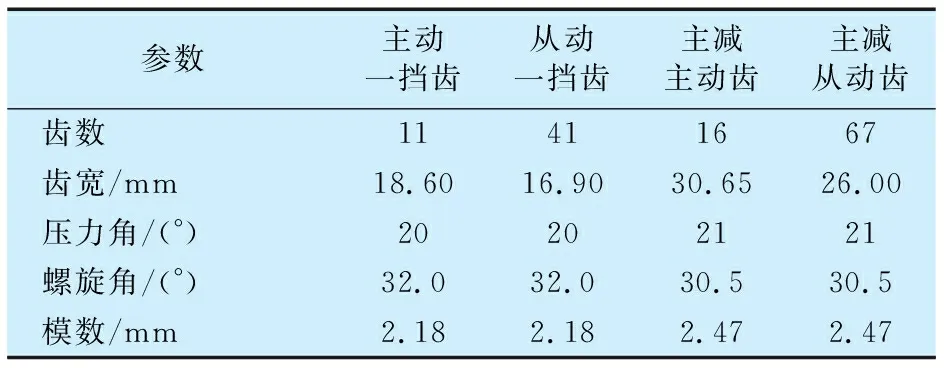
表3 变速箱齿轮参数Tab.3 Transmission gear parameters

MASTA是一款针对传递系统选配、设计和开发的专用软件，它基于理论公式，计算结果更加准确。根据齿轮、轴承参数建立的MASTA分析系统模型如图4所示。

图4 MASTA分析系统模型Fig.4 MASTA analysis system model

3 考虑油沟影响修正轴承分析模型

为减少热处理变形裂纹，套圈滚道与油沟之间圆弧过渡，过渡区域作为油沟的一部分。滚子末端与倒角圆滑过渡，过渡区域作为滚子倒角的一部分。

3.1 滚子对数修形

根据滚子最小凸度0.018 mm及初始评价长度L1(规定修形量所对应的评价长度)，确定Lundberg对数修形曲线如图5所示。当油沟宽度超过滚子倒角时，滚子实际接触长度减小到L2。在MASTA中滚子凸度选择取点自定义，修形为对数修形中的L2部分。

图5 Lundberg对数修形曲线Fig.5 Lundberg logarithmic profiling curve

MASTA软件计算中接触长度为滚子有效长度Lwe。需通过虚拟增大滚子倒角来定义实际接触长度，MASTA中设置滚子倒角为R=r+(L1-L2)/2。

3.2 内、外圈全圆弧修形

内、外圈全圆弧修形，沿滚道接触位置的曲率半径一致，在MASTA模型中通常按圆弧半径设置。

根据内、外圈最小修形量以及初始评价长度(内圈为L2，外圈为L3)，内圈全圆弧修形半径为5 800 mm,外圈全圆弧修形半径为18 000 mm，如图6所示。考虑油沟时，因油沟在内圈上，内圈滚道修正长度与L2一致。外圈滚道修正长度会减小至L4=Lwe=L-2r，内、外圈实际修形量为修正长度L2和L4所对应的凸度。

图6 套圈全圆弧修形Fig.6 Ring full arc profiling

4 考虑油沟的边缘应力计算和设计优化

4.1 应力计算

考虑油沟时失效套圈边缘应力计算结果如图7所示，边缘应力到达4 000 MPa。故需优化轴承结构参数，消除边缘应力。

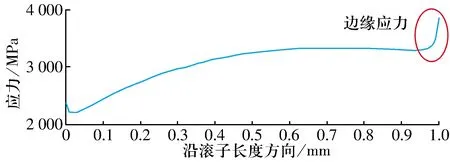
图7 考虑油沟时内圈边缘应力Fig.7 Inner ring edge stress with considering oil groove

4.2 许用油沟宽度分析

4.2.1 最大油沟宽度计算

不同油沟宽度时内圈最大应力和边缘应力如图8所示：1)当油沟宽度小于0.97 mm时，随油沟宽度增大，内圈最大应力略微增加；2)当油沟宽度继续增大到1.04 mm时，出现边缘应力，边缘应力随油沟宽度增大而增大，油沟宽度为1.24 mm时，边缘应力达到4 000 MPa。为避免边缘应力，输出轴前端轴承油沟宽度应控制在0.97 mm以内。

图8 内圈应力与油沟宽度的关系Fig.8 Relationship between inner ring stress and oil groove width

4.2.2 许用油沟宽度与修形量的关系

当油沟宽度要求太小时，磨加工时可能会产生留边，为避免出现此现象，可适当增加滚子修形量。考虑油沟宽度计算内圈边缘应力，得到轴承许用油沟宽度与滚子最小修形量的关系如图9所示。

图9 滚子最小修形量与许用油沟宽度的关系Fig.9 Relationship between minimum amount of roller profiling and allowable oil groove width

4.2.3 许用油沟宽度与轴承偏载角的关系

根据接触理论：轴承系统变形引起的偏载角(偏载时套圈轴线与滚子轴线的夹角)越大，越易产生边缘应力，要求油沟宽度也越小。通过调整系统分析模型轴的刚度来调整轴承偏载角，同样考虑油沟宽度计算内圈边缘应力，得到轴承许用油沟宽度与轴承偏载角的关系如图10所示。

图10 轴承偏载角与许用油沟宽度的关系Fig.10 Relationship between eccentric load angle of bearing and allowable oil groove width

4.3 设计优化及验证

综合考虑滚子修形量、系统偏载角及安全余量，得到油沟最大宽度为0.7 mm。对油沟优化后的轴承(油沟宽度为0.7 mm)进行变速箱总成耐久试验，试验后拆解轴承(图11)，无边缘应力出现。

图11 变速箱总成耐久试验后轴承拆解结果Fig.11 Disassembly result of bearing after durability test of gearbox assembly

5 结论

建立了一种考虑油沟时轴承边缘应力的计算方法，并分析了油沟宽度与内圈边缘应力、滚子修形量、轴承偏载角的关系，得出结论：

1)滚子修形量越大，许用油沟宽度越大；

2)轴承系统变形引起的偏载角越大，许用油沟宽度越小。