冲击工况下高速圆锥滚子轴承保持架动力学分析
呙如兵,时大方,张晶,杨帆,张弘毅
(1.中车戚墅堰机车车辆工艺研究所有限公司,江苏 常州 213011;2.浙江天马轴承集团有限公司,浙江 湖州 313219;3.洛阳轴承研究所有限公司,河南 洛阳 471039)
轨道交通车辆齿轮箱轴承是列车运行的重要部件,其工作状态将直接影响车辆的安全运转。轨道交通车辆工况复杂,特别是冲击载荷会导致保持架运转不稳定,从而引发轴承失效,故有必要对轨道交通车辆齿轮箱轴承保持架进行动力学分析。
近年来,国内外学者对轴承动力学做了大量研究:文献[1]建立了滚动轴承各零件动力学方程,得到各零件间的接触载荷、滑动速度和刚度等;文献[2]基于前人的理论研究,使用弹簧等效各零件间的接触,简化了动力学计算过程;文献[3]基于ADAMS分析了圆锥滚子轴承动力学特性,确定了最佳工况参数;文献[4]建立铁路货车轴承动力学模型,基于ADAMS开展故障仿真分析,得出不同故障程度下轴承的动力学特性;文献[5]建立高速角接触球轴承动力学模型,分析了不同载荷条件下保持架的运动规律;文献[6]建立高速圆柱滚子轴承保持架动力学微分方程,分析了引导方式对保持架质心轨迹和打滑率的影响;文献[7]建立高速球轴承保持架有限元模型,分析兜孔间隙和引导间隙对保持架动态特性的影响;文献[8]基于ANSYS/LS-DYNA,考虑圆锥滚子轴承零件间的弹性变形和动态接触,建立高速圆锥滚子轴承动力学模型,分析故障条件下轴承的动态特性。
上述轴承动力学模型均未考虑润滑油膜和冲击载荷的作用,而轨道交通车辆齿轮箱用圆锥滚子轴承同时受齿轮啮合产生的轴向、径向载荷及来自轨道的冲击载荷。鉴于此,考虑上述载荷的联合作用和润滑油膜的影响,建立圆锥滚子轴承动力学模型,分析圆锥滚子轴承保持架动力学特性。
1 圆锥滚子轴承受力分析
建立圆锥滚子轴承整体坐标系和各零件局部坐标系,轴承整体坐标系Oxyz,内圈坐标系Oixiyizi,滚子局部坐标系Orxryrzr,保持架局部坐标系Ocxcyczc,如图1所示。

图1 圆锥滚子轴承坐标系示意图Fig.1 Diagram of tapered roller bearing coordinate system
1.1 滚子与内外圈滚道的相互作用
第j个滚子与滚道之间的法向接触力为
(1)
式中:Qi(e)jk为第j个滚子的第k个切片与内、外圈滚道的法向接触力(图2);E′为滚子与套圈材料的当量弹性模量;δi(e)jk为第j个滚子的第k个切片与内、外圈的接触变形量;L为滚子长度;n为切片数量。

图2 滚子切片受力分析Fig.2 Force analysis of roller slices
受联合载荷时,滚子会出现倾斜和歪斜,第j个滚子的第k个切片上的法向接触力会产生平衡滚子倾斜的抵抗力矩,第j个滚子与内、外圈的接触力产生的抵抗力矩为
(2)
MQi(e)jk=Qi(e)jkhsignβx,
lk=kΔz,
ε=(αe-αi)/2,
式中:βx为滚子歪斜角;lk为第k个滚子距滚子端面的长度;dw为滚子大端直径;h为滚子端面与大挡边的接触高度;ε为滚子半锥角;l′为滚子质心距滚子大端面的距离;Δz为切片宽度;αi,αe分别为内、外圈接触角。
润滑油的存在会使滚子与滚道之间形成润滑油膜,根据油膜拖动力可求得滚子与滚道之间的摩擦力,第j个滚子所受拖动力为
(3)
Ti(e)jk=μQi(e)jk,
式中:Ti(e)jk为第j个滚子的第k个切片与内、外圈滚道的拖动力;μ为油膜拖动系数,可根据文献[9-10]计算。
第j个滚子在拖动力作用下的歪斜力矩为
(4)
MTi(e)jk=Ti(e)jkh′signβy,
h′=kΔz-l′,
式中:MTi(e)jk为第j滚子的第k个切片与内、外圈滚道在拖动力作用下的歪斜力矩;βy为滚子歪斜角。
1.2 滚子大端面与内圈大挡边的相互作用
第j个滚子大端面与内圈大挡边的接触力为
(5)
式中:Kj为载荷-变形系数;δ为弹性变形量;nδ为端面大挡边接触弹性系数;η为综合弹性系数;∑ρ为接触点曲率和。
第j个滚子因歪斜和倾斜产生的力矩为
MQfxj=QfjL1sinβx,
(6)
MQfyj=QfjL1sinβy,
(7)
式中:L1为滚子歪斜中心距大端面的距离。
第j个滚子大端面与内圈大挡边的油膜拖动力为
Ffj=μQfj,
(8)
则由摩擦力产生的力矩为
(9)
1.3 滚子与保持架的相互作用
滚子与保持架的相互作用如图3所示,滚子与保持架的接触力、拖动力分别为

图3 滚子与保持架的相互作用Fig.3 Interaction between roller and cage
(10)
(11)
式中:Qcj1,Qcj2为第j个滚子与保持架兜孔的接触力;Ffcj1,Ffcj2为第j个滚子与保持架的拖动力。
滚子所受摩擦力矩为
(12)
式中:rjk为第j个滚子的第k个切片的半径;ds为滚子小端直径。
滚子发生歪斜时会与保持架兜孔发生碰撞,此时两者会产生平衡滚子歪斜的抵抗力矩,滚子抵抗歪斜的力矩为
(13)
1.4 保持架与引导套圈的相互作用
保持架受力如图4所示,引导面上的作用力和作用力矩为

图4 保持架受力示意图Fig.4 Force diagram of cage
(14)
(15)
(16)
式中:η0为油膜动力黏度;R为引导面半径;B为引导面宽度;e为偏心距;Cg为引导间隙;ωc为保持架转速;ω为引导套圈转速;φ为第j个滚子位置角。
在坐标系Oxyz中,Fcn,Fcτ,Mc可表示为
(17)
1.5 保持架动力学方程
根据保持架受力情况,得到保持架动力学方程为

(18)
式中:mc为保持架质量;Gc为保持架重力;Jc为保持架转动惯量;dc为滚子与保持架接触点的直径(图4);Z为滚子数。
同理,根据滚子、内圈受力情况,可建立滚子和内圈动力学方程。
2 圆锥滚子轴承保持架动力学模型
2.1 主要结构参数及材料参数
以某轨道交通车辆用圆锥滚子轴承为例,其主要结构参数见表1。保持架材料为08AL,滚子及内外圈材料为GCr15,材料参数见表2。采用4109润滑油,油温设置为70 ℃。

表1 圆锥滚子轴承主要结构参数Tab.1 Main structural parameters of tapered roller bearing

表2 圆锥滚子轴承零件材料参数Tab.2 Material parameters of tapered roller bearing parts
2.2 网格划分和接触设置
基于UG软件建模,导入ANSYS/LS-DYNA,建立轴承动力学分析模型,如图5所示。在网格划分过程中,采用SOLID164四面体单元,采用扫略、映射和自由划分相结合的方式进行网格划分,接触区域网格细化,以提高计算精度。接触设置为面-面接触,根据轴承的工作特点,在滚子与内圈、滚子与外圈、滚子与保持架、保持架与外圈之间建立了112组接触对,综合考虑轴承零件的材料和实际工况选择各接触面的静、动摩擦因数,见表3。

图5 圆锥滚子轴承动力学模型Fig.5 Dynamic model of tapered roller bearing

表3 接触面摩擦因数Tab.3 Friction coefficient of contact surface
2.3 边界条件和载荷的设置
根据轴承的实际工况条件,外圈外表面施加全约束,内圈内表面施加径向力和轴向力,约束内圈内表面绕x,y轴的旋转。
2.4 工况条件
在正常载荷和冲击载荷(表4)两种工况下分析保持架动力学特性。兜孔间隙分别为0.20,0.25,0.30 mm,引导间隙分别为0.15,0.20,0.25 mm。

表4 工况参数Tab.4 Operating condition parameters
3 结果分析
基于LS-DYNA软件的二次开发语言APDL参数化编程实现轴承动力学计算,输出计算结果后再计算轴承零件各接触面的摩擦力和摩擦力矩,代入轴承动力学程序中计算。在正常载荷和冲击载荷两种工况下分析兜孔间隙和引导间隙对保持架动力学特性的影响。
3.1 兜孔间隙对保持架动力学特性的影响
引导间隙0.20 mm时不同兜孔间隙下保持架质心运动轨迹如图6所示:1)当兜孔间隙为0.20 mm时,正常载荷下保持架质心运动轨迹涡动半径为规则圆形,冲击载荷下保持架涡动半径较小,x方向窜动较小,质心运转稳定;2)当兜孔间隙增加到0.25 mm时,正常载荷下保持架质心运动轨迹较为稳定,但涡动半径增大,冲击载荷下保持架质心运动紊乱,x方向窜动较大,保持架运转不稳定;3)当兜孔间隙增加到0.30 mm时,正常载荷下保持架质心运动轨迹呈不规则形状,冲击载荷下随兜孔间隙增大,保持架运转更不稳定。

图6 引导间隙0.20 mm时不同兜孔间隙下保持架质心运动轨迹Fig.6 Cage center of mass motion trajectory under different pocket clearances when guiding clearance is 0.20 mm
引导间隙0.20 mm时不同兜孔间隙下保持架应力云图如图7所示:1)当兜孔间隙为0.20 mm时,正常载荷下保持架应力最大值为45.2 MPa,冲击载荷下保持架应力最大值为178.1 MPa;2)当兜孔间隙增加到0.25 mm时,正常载荷下保持架应力最大值为31.7 MPa,冲击载荷下保持架应力最大值为164.4 MPa;3)当兜孔间隙增加到0.30 mm时,正常载荷下保持架应力最大值减小为26.8 MPa,冲击载荷下保持架应力最大值减小为153.7 MPa。

图7 引导间隙0.20 mm时不同兜孔间隙下保持架应力云图Fig.7 Cage stress nephogram under different pocket clearances when the guiding clearance is 0.20 mm
由上述数据可知:正常载荷下保持架应力远小于保持架屈服强度(190 MPa),冲击载荷下保持架应力虽然较大,但也未超过保持架屈服强度;两种载荷下保持架应力均呈逐渐减小的趋势,这是由于兜孔间隙较小时滚子与保持架碰撞力较大,兜孔间隙增大会使滚子与保持架碰撞力减小。
3.2 引导间隙对保持架动力学特性的影响
兜孔间隙0.25 mm时不同引导间隙下保持架质心运动轨迹如图8所示:1)当引导间隙为0.15 mm时,与图6c、图6d对比,随引导间隙减小,正常载荷下保持架质心运动轨迹涡动半径增大,冲击载荷下保持架质心运动轨迹呈较为杂乱的运动轨迹,x和y方向窜动增大,保持架运转变得不稳定,将加速保持架磨损;2)当引导间隙为0.25 mm时,正常载荷下保持架涡动半径减小,冲击载荷下保持架质心运动轨迹呈较规则的圆形,保持架窜动大大减小。
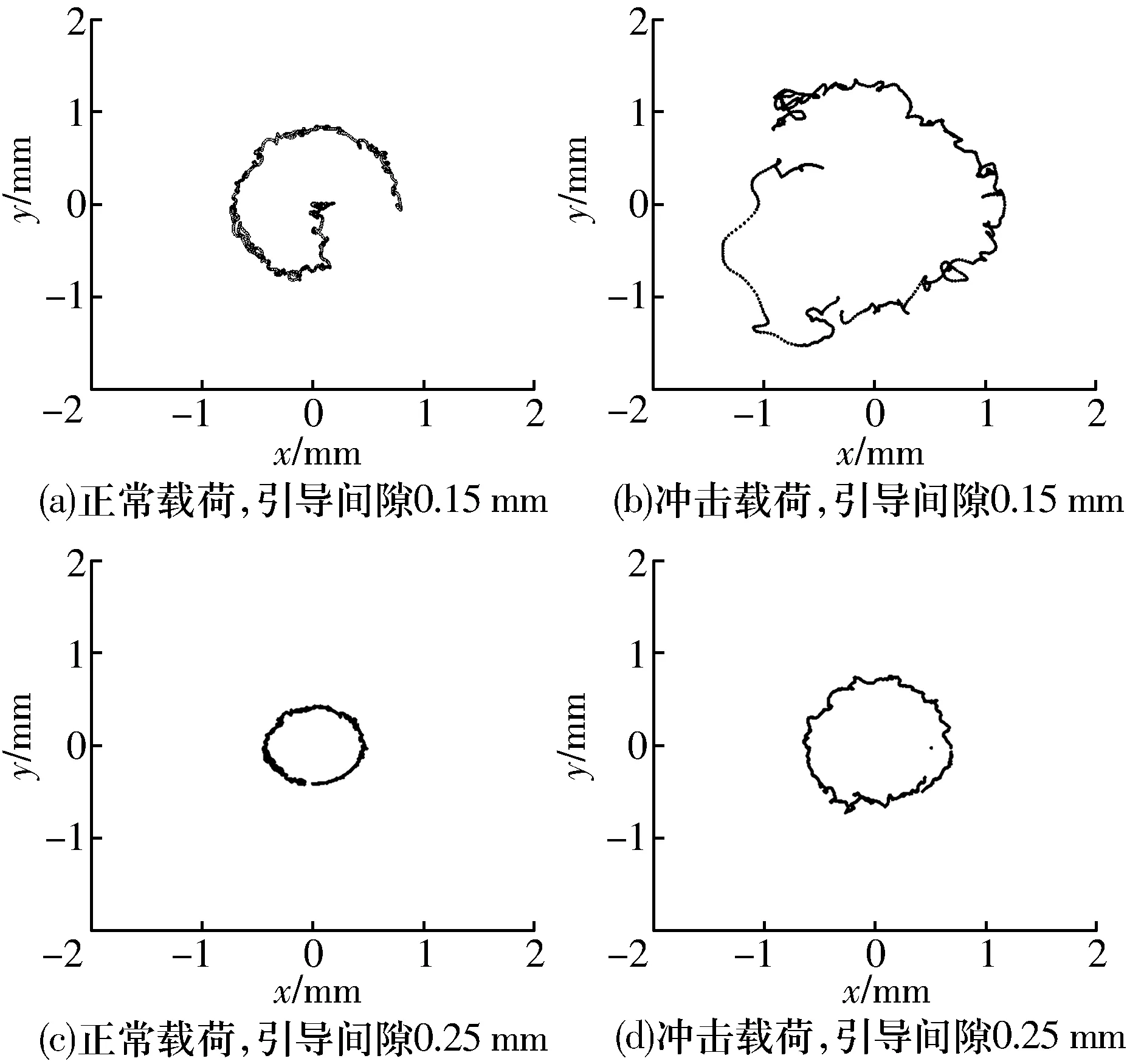
图8 兜孔间隙0.25 mm时不同引导间隙下保持架质心运动轨迹Fig.8 Cage center of mass motion trajectory under different pocket clearances when guiding clearance is 0.25 mm
兜孔间隙0.25 mm时不同引导间隙下保持架应力云图如图9所示:1)当引导间隙为0.15 mm时,与图7c、图7d对比,随引导间隙减小保持架应力略有减小,正常载荷下保持架应力最大值为23.6 MPa,冲击载荷下保持架应力最大值为148.8 MPa;2)当引导间隙为0.25 mm时,与图7c、图7d对比,随引导间隙增大保持架应力略有增大,正常载荷下保持架应力最大值为35.7 MPa,冲击载荷下保持架应力最大值增加至164.8 MPa,但未超过保持架屈服强度。

图9 兜孔间隙0.25 mm时不同引导间隙下保持架应力云图Fig.9 Cage stress nephogram under different guiding clearances when pocket gaps is 0.25 mm
4 结论
基于ANSYS/LS-DYNA软件,考虑滚子与滚道、滚子与保持架、保持架与套圈的相互作用,建立轨道交通车辆齿轮箱用圆锥滚子轴承动力学模型,考虑径向载荷、轴向载荷和冲击载荷的作用,分析兜孔间隙和引导间隙对保持架动力学特性的影响,得出以下结论:
1)冲击载荷将使圆锥滚子轴承保持架质心运动轨迹的涡动半径增大,保持架质心运动不稳定,保持架应力增大。
2)随兜孔间隙增大,保持架质心运动轨迹的涡动半径增大,保持架应力减小。
3)随引导间隙增大,保持架质心运动轨迹的涡动半径减小,保持架应力增大。

