基于热气弹耦合的悬臂式箔片气体动压轴承动态特性分析

魏训涛，尹明虎，张龙，韩扬，寇名仕

(1.兖州煤业股份有限公司 设备管理中心，山东 济宁 273500；2.兖矿集团 博士后科研工作站，山东 济宁 273500；3.西安理工大学 机械与精密仪器工程学院，西安 712048)

1 概述

相较于传统液体动压轴承，气体轴承以黏度远低于液体的空气(或惰性气体等其他气体)作为润滑介质，可使轴承在转速提高5～10倍，支承精度提高2个数量级的基础上降低3个数量级的功耗，使轴承工作寿命提高了数十倍[1]。而且，气体轴承无污染，可在低温和高温中使用等优点使其成为高速、低摩擦、高精密及特殊工况下支承的首选方案，在军事、航空、航天、医疗等高新技术行业得到了广泛认可及应用。

箔片气体动压轴承是气体轴承的一种重要形式，其利用具有挠性支承结构的箔片构成轴瓦，很好抑制了动压轴承的涡动现象。箔片气体动压轴承有悬臂式、张紧式、缠绕式、波箔式和多楔式等多种结构形式,本文的研究对象——悬臂式箔片气体轴承如图1所示，其轴瓦由若干箔片沿轴承内壁均匀重叠排列组成，箔片一端固定在轴承座的凹槽内，另一端则与相邻箔片互相叠搭[2-3]。

图1 悬臂式箔片气体轴承结构简图Fig.1 Structure diagram of cantilever type foil aerodynamic bearing

悬臂式箔片气体轴承在军事和航空领域的应用价值和潜力对其发展起到了巨大的推动作用，并成为相关领域的研究热点[3]。文献[4]采用增量有限元法求解可压缩雷诺方程，获得了悬臂式箔片气体轴承的静、动态特性，并分析了压缩性系数、箔片刚度等对其性能的影响；文献[5]利用刚柔接触理论研究了大预紧力下悬臂式箔片气体轴承的非线性接触行为；文献[6]研究了以氮气和氧气作为润滑介质的悬臂式箔片气体轴承的静、动态特性；文献[7-8]针对透平机械中使用的大直径悬臂式箔片气体轴承，开发了测量其承载能力的试验装置，并基于动网格技术的CFD仿真获得了轴承的动态特性系数；文献[9]在考虑安装预紧力及箔片型面精度的条件下，通过试验对悬臂式箔片气体轴承的承载能力及动态特性系数进行了分析，研究表明通过控制预紧力及型面精度可调整轴承的承载能力、刚度和阻尼；文献[10]研究了悬臂式箔片气体轴承中相邻箔片间的面接触问题；文献[11]对某悬臂式箔片气体轴承进行了原理性试验；文献[12]对某涡轮冷却器用悬臂式箔片气体轴承进行了静态加载和运行试验；文献[13]运用弹性力学理论对悬臂式箔片气体轴承的箔片变形进行了分析；文献[14]基于几何分析建立了悬臂式箔片气体轴承预紧力的计算方法，并通过有限元仿真验证了其可靠性；文献[15]分析了扰动频率对悬臂式箔片气体轴承刚度和阻尼系数的影响；文献[16-17]研究了悬臂式箔片气体轴承的弹性变形及温度场；文献[18-19]在等温假设条件下分析了悬臂式箔片气体轴承的静、动态特性；文献[20]分析了悬臂式箔片气体轴承的稳定性；文献[21]通过试验研究了悬臂式箔片气体轴承支承的转子系统的振动特性；文献[22]在考虑箔片间及箔片与转子间接触的条件下，分析了结构参数对悬臂式箔片气体轴承的影响。

从上述研究可以看出，悬臂式箔片气体轴承主要应用于高速/超高速转子系统的支承，轴承的动态特性对整个转子系统的稳定性至关重要。因此，综合考虑悬臂式箔片气体轴承工作过程中的流体动压效应、箔片变形及热效应等因素，基于雷诺方程、能量方程、箔片弹性变形方程、热平衡方程等建立了热气弹耦合条件下的悬臂式箔片气体轴承性能计算模型，并重点分析箔片数目、长径比等对其动态特性(刚度系数和阻尼系数)的影响。

2 理论计算模型

建立悬臂式箔片气体轴承热气弹耦合性能计算模型，须综合考虑轴承工作过程中的流体动压效应、箔片变形及热效应。因此，分别建立考虑箔片弹性变形的气膜厚度方程、可压缩流体的雷诺方程、考虑传热及对流换热的能量方程，通过上述方程的耦合实现热气弹耦合条件下轴承的性能计算。

2.1 考虑箔片弹性变形的气膜厚度方程

悬臂式箔片气体轴承内的几何关系如图2所示，某箔片一端固定在轴承壳A点，另一端与后一箔片在B点搭接，前一箔片则与此箔片在S点搭接，图中C点为此箔片的曲率中心，虚线圆为各箔片曲率中心形成的半径Rg的生成圆。由图中几何关系可得，此箔片上的气膜厚度h为

图2 悬臂式箔片气体轴承内的几何关系Fig.2 Internal geometrical relationship of cantilever type foil aerodynamic bearing

(1)

式中：Rf为箔片半径；α，τ分别为以轴承中心、箔片中心为极心的坐标系下的角度；Disp为箔片径向变形，下标i为箔片编号；e为轴承偏心距。

(2)

考虑到箔片为柱形薄壳，由弹性薄壳力学的相关知识可知，基于柱形薄壳的几何尺寸有3种计算方法：边长比大于3的柱形壳，用梁理论；边长比为0.5～3.0的中长壳，用有矩理论；边长比小于0.5的短壳，用无矩理论[13]。对于悬臂式箔片气体轴承而言，箔片的长径比一般为0.5～3.0且比箔片的厚度大得多，因此采用计算柱形薄壳弹性变形的有矩理论计算箔片的弹性变形。对箔片微元体进行受力分析，可得其变形方程为

(3)

(4)

(5)

2.2 雷诺方程

忽略流体惯性力，由纳维-斯托克斯方程(N-S方程)推导出描述轴承内气膜压力的可压缩气体雷诺方程，即

(6)

式中：p为气膜压力；U为轴颈的圆周速度；ρ为气体密度；η为气体动力黏度。

(7)

考虑到箔片搭接处的结构突变及气体压力、温度、密度三者间的耦合关系，在模型中纳入了流量连续性方程及气体状态方程，即

(8)

式中：u，v和w为流体沿各x，y，z坐标方向的速度(z为轴承宽度方向，垂直于图2所示的xOy平面)；R为理想气体常数；T为温度。

2.3 考虑传热及对流换热的能量方程

基于功能原理，考虑气膜工作时的对流换热和摩擦生热，得到了描述轴承内温度分布的能量方程，即

(9)

式中：cv为气体比热容。

(10)

式中：cva为标准大气压及室温条件下的气体比热容；Ta为室温。

同时，考虑气膜与箔片、箔片与外界空气之间的热交换可得

(11)

式中：λi为气膜与箔片之间的受迫对流换热系数；λo为箔片与外界空气之间的自然对流换热系数；κ为箔片热导率；Tg，Tb和To分别为气膜、箔片和外界空气的温度。

2.4 性能计算流程

联立(1)—(11)式并采用有限差分法求解，获得热气弹耦合条件下悬臂式箔片气体轴承内的气膜压力分布、温度分布、轴承承载力、轴承刚度、阻尼等特性参数。计算流程如图3所示，采用Matlab编程求解，程序收敛条件为相邻2次迭代计算所得气膜压力之间的误差小于0.5%。

图3 悬臂式箔片气体轴承性能计算流程Fig.3 Performance calculation process of cantilever type foil aerodynamic bearing

计算过程中采用雷诺边界条件，即

(12)

各箔片上的量纲一的气膜承载力可由气膜压力的积分计算，即

(13)

对应的气膜承载力为

(14)

整个轴承的承载力可由各箔片上气膜力合成得出。

采用小扰动法进行悬臂式箔片气体轴承动态特性系数的计算，给定微小的位移扰动和速度扰动，分别计算扰动前后轴承承载力的变化量，通过轴承承载力变化量与对应扰动量之比得到量纲一的刚度系数K和阻尼系数D，即

(15)

(16)

轴承刚度系数k(N/mm)和阻尼系数d(N·s·mm-1)为

(17)

2.5 模型验证

某悬臂式箔片气体轴承的基本参数见表1，偏心率为0.8时，该悬臂式箔片气体轴承的气膜压力分布及温度分布如图4所示(计算时每片箔片网格为40×20,轴向方向表示量纲一的轴承宽度)，由图可知：由于箔片搭接处存在结构突变而导致气膜厚度发生了突变，轴承的气膜压力分布及气膜温度分布均出现了明显波动，气膜压力最大值附近即为气膜温度最高处，与相关文献[19-20]的计算结果一致。

表1 悬臂式箔片气体轴承的基本参数Tab.1 Basic parameters of cantilever type foil aerodynamic bearing

图4 悬臂式箔片气体轴承的气膜压力及温度分布Fig.4 Gas film pressure and temperature distributions of cantilever type foil aerodynamic bearing

为进一步验证本文所建模型的可靠性，采用该模型对文献[23]中的悬臂箔片气体轴承进行性能计算，结果如图5所示，由图可知：本文计算结果与文献[23]理论计算结果十分接近，文献[23]在等温假设下进行建模及理论计算但并未给出温度的具体取值，本文按室温25 ℃进行热气弹耦合性能计算，故两者的计算结果存在一些差异；由于本文及文献[23]理论计算中均未考虑转子自重的影响，理论计算结果与试验结果存在一定差异，但与文献[23]试验结果的变化趋势有很好的一致性，也一定程度上证明了本文模型的可靠性。

图5 文献[23]中悬臂式箔片气体轴承气膜承载力计算结果的对比Fig.5 Results comparison between reference[23]and this paper on gas film load capability of cantilever type foil aerodynamic bearing

3 轴承动态特性分析

基于建立的悬臂式箔片气体动压轴承热气弹耦合性能计算模型，分析箔片数目N、长径比L、偏心率ξ对轴承动态特性系数(刚度系数和阻尼系数)的影响，分析所用轴承的基本结构及工况参数见表1。

不同偏心率下，箔片数目(L=0.8)和长径比(N=10)对轴承刚度系数k的影响如图6所示，由图可知：1)随着箔片数目的增加，箔片悬臂段的长度逐渐减小，箔片的刚度系数逐渐增大，从而导致相同偏心率下箔片的弹性变形逐渐减小，气膜厚度逐渐减小，轴承刚度系数逐渐增加；2)随着长径比的增加，轴承的承载面积逐渐增大，气体端泄阻力亦增大，进而导致相同偏心率下轴承的承载力逐渐增大，轴承刚度系数也逐渐增大。

图6 不同偏心率下，箔片数目和长径比对刚度系数的影响Fig.6 Influence of foil number and length-diameter ratio on stiffness coefficient under different eccentricities

此外，不同于液体滑动轴承，当偏心率增加到一定数值后，轴承刚度系数出现了降低的现象，这正是弹性箔片自适应调节作用的体现。在大偏心率下，轴承承载较大，箔片会产生较大的变形以调整气膜厚度，从而使气膜承载力略有降低，轴承刚度系数亦有所降低，如图7所示。

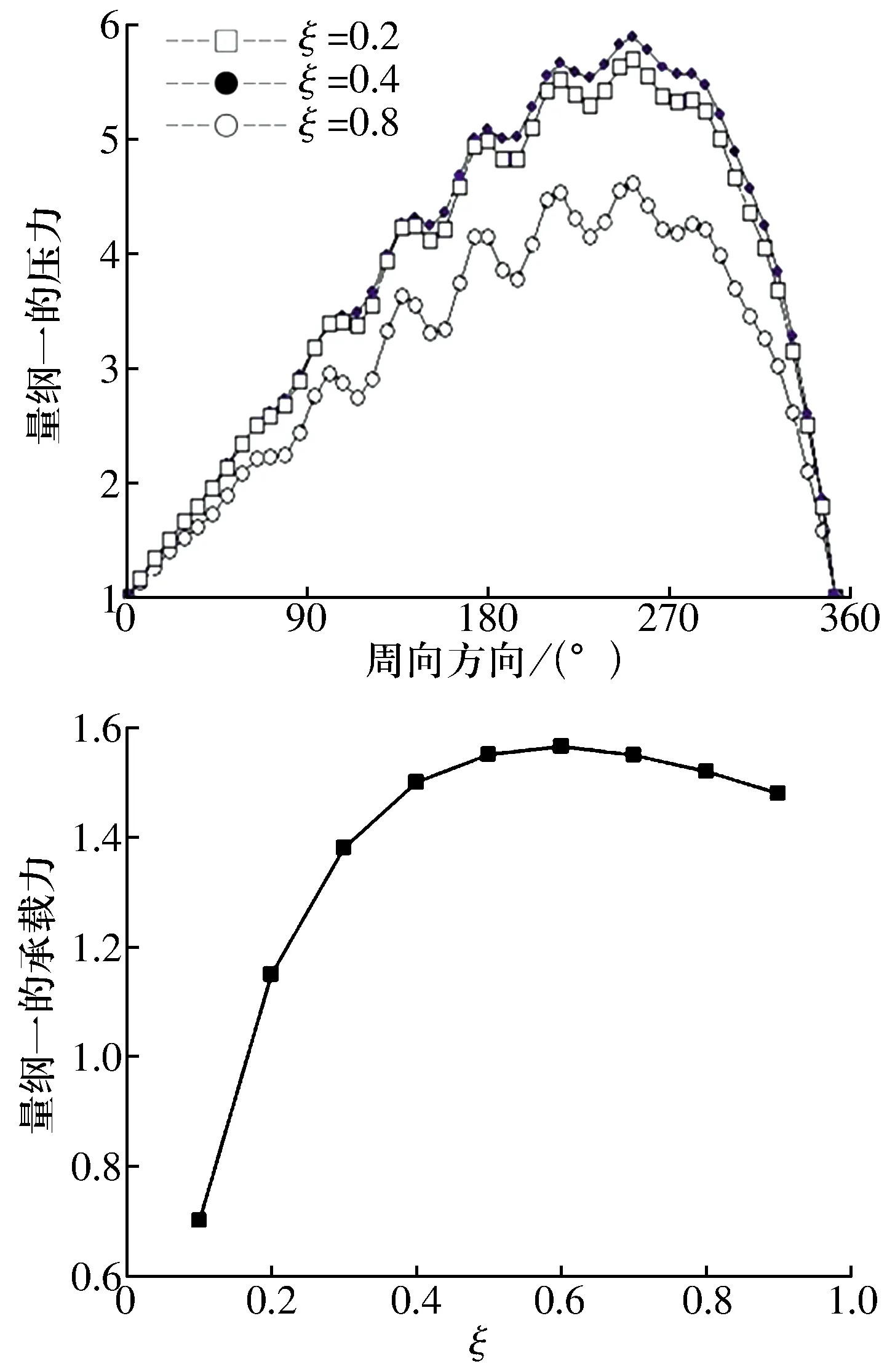
图7 不同偏心率下轴承的气膜压力及承载力Fig.7 Gas film pressures and load capacity of bearing under different eccentricities

不同偏心率下，箔片数目(L=0.8)和长径比(N=10)对轴承阻尼系数D影响的计算结果见表2，由表可知：相较于轴承刚度系数，偏心率、箔片数目和长径比对轴承阻尼的影响较为复杂；总的来说，随着箔片数目和长径比的增加，轴承承载力逐渐增大，轴承阻尼系数也呈现逐渐增大的趋势；在偏心率从0.2增加至0.6的过程中，轴承阻尼系数随偏心率的增加而逐渐增大；但在偏心率为0.8时，主阻尼系数Dyy出现了下降，交叉阻尼系数Dxy甚至出现了负数(表中黄色标出的数据)，这可能是由于大偏心率下箔片变形较大，气膜不稳定所导致。

表2 不同偏心率、箔片数目及长径比下的轴承阻尼系数Tab.2 Damping coefficient of bearing under different eccentricities, foil numbers and length-diameter ratios

4 结论

基于箔片变形方程、气膜厚度方程、雷诺方程、能量方程建立了悬臂式箔片气体轴承的热气弹耦合性能计算模型，并据此分析了箔片数目、长径比、偏心率对轴承动态特性系数的影响，可得出以下结论：

1)箔片数目的增加减小了箔片的悬臂段长度，增大了箔片刚度系数，减小了气膜厚度，轴承刚度系数和阻尼系数随箔片数目的增加逐渐增大。

2)长径比的增加增大了轴承承载面积，加大了气体端泄阻力，增大了轴承承载力，轴承刚度系数和阻尼系数随长径比的增加而逐渐增大。

3)由于弹性箔片的自适应性，在大偏心率下可产生较大的变形以维持合理的气膜厚度，因此随着偏心率的增加，轴承刚度系数先增大后减小；在大偏心率下(本文结果显示为0.8左右)，轴承阻尼系数则呈现出较为复杂的变化规律。

通过本文分析可知，悬臂式箔片气体动压轴承动态特性与箔片数目及结构息息相关，对于悬臂式箔片气体动压轴承支承的转子系统而言，可通过优化箔片数目、厚度、长径比等结构参数提升系统动态性能及稳定性。