自抗扰锁相跟踪系统设计与仿真

黄文超,刘 泽,赵思泽,王铭伟,李俊杰

(北京交通大学电子信息工程学院，北京 100044)

0 引言

锁相跟踪校准是锁相环技术的重要组成部分，目前锁相环技术已经被广泛应用在通信、雷达、仪器仪表和数字电视等领域。锁相环(phase locked loop)是指一种电路或者模块，其功能为对接收到的信号进行处理，并从其中提取某个时钟的相位信息。或者说，对于接收到的信号，产生一个时钟信号，使得输出的信号与输入的信号从某种角度来看是同步的[1]。在经典锁相环结构中，鉴相器输出参考信号和分频器输出信号的相位差信号，经过环路滤波器的滤除高频分量后将信号输入到压控振荡器，改变振荡器的振荡频率，在闭环负反馈控制下输出信号与分频器的相位差保持不变，锁相环进入锁定状态。本文的锁相跟踪的目的是让控制信号与参考信号的相位误差在一个较小的范围，即达到同步。

经典PID控制原理是用误差的过去、现在和变化的趋势来进行加权控制，能满足实际中的大量应用，但不能满足在计量中的高性能要求。自抗扰控制器ADRC(auto disturbances rejection controller)技术结合了PID技术的精髓并吸取现代控制理论成就,不需要提供被控对象的精确数学模型，能够替代 PID 控制技术，系统的扰动无需测量，解耦控制易于实现，已经在控制领域中广泛地应用并取得了令人满意的效果。本文使用数字频率合成器DDS(direct digital synthesis)作为信号源，通过不断地求取信号源信号和参考信号的参考误差，运用改进自抗扰控制算法得到相应的频率控制字，使控制信号与参考信号保持同步[2-4]。

1 自抗扰锁相跟踪系统结构与原理

自抗扰锁相跟踪系统结构如图1所示，该系统主要包含5个部分：二阶广义积分器、求取相位、非周期化、ADRC和DDS。二阶广义积分器将参考信号分解成2个正交信号α和β，分别作为复数的实部和虚部，通过计算该复数的辐角得到参考信号的准确相位。由于相位呈周期变化，不利于自抗扰控制算法的引入，需要对其进行非周期化的处理。DDS信号发生器采用直接数字频率合成技术，随着近些年超高速电路的发展和对该技术的深入研究，DDS信号发生器的频率稳定度、准确度已经提高到与基准频率相同的水平，并且可以在很宽的频率范围内进行精细的频率调节。采用这种方法设计的信号源可工作于调制状态，可对输出电平进行调节，也可输出各种波形。参考信号和控制信号的相位分别输入自抗扰控制算法中，通过该算法得到DDS的频率控制字并有效地抑制了不确定扰动。DDS技术中频率转换时间在超高速时钟频率中可达到纳秒级别[5]。该控制系统具有优秀的抗干扰性和实时性。

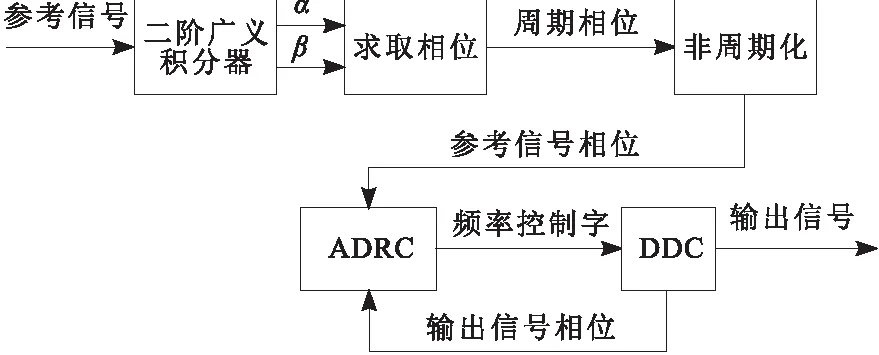
图1 自抗扰锁相跟踪系统结构

1.1 系统参考信号相位的准确获取

参考信号的输入仅为一个正弦波，信息量不足以获取信号的准确相位，需要再构造一个与参考信号相位偏差90°的正交信号。通过代入复数，形成的复数辐角即为该参考信号的精确相位。利用希尔伯特变换可以得到该正交信号，计算量比较大，会耗费较多的运算资源并且影响系统的实时性和准确性[6]。还一种方法比较简单，将信号传输延迟1/4周期的时间，不过不容易控制且误差会比较大。电网并网中常用的二阶广义积分器产生正交信号的同时[7]，还具有滤波效果。

图2为二阶广义积分器的结构，α和β是2路正交信号，其中α与参考信号具有相同的相位，β与参考信号的相位相差1/4周期。

图2 二阶广义积分器结构

由图2中结构可知，α和β的传递函数表达式为：

(1)

(2)

k为待定系数；ω为二阶广义积分的谐振频率，需要与参考信号的频率保持一致。当k取不同值时，系统的性能会发生变化。

假定输入信号的频率为50 Hz，即314 rad/s,从相频响应中可以发现，对于式(1)，响应信号和输入信号在基频ω处保持同一相位，而对于式(2),则滞后90°。从幅频响应中可以发现该系统具有一定的滤波效果。另外k值越大，系统响应越快，带宽也越大，但是滤波性和选通性都会越小[8]。综合考虑后，选取k值为0.7。

1.2 系统的精确频率合成

数字频率合成器结构如图3所示，其工作原理类似于计数器，每来1个时钟脉冲，频率控制字就累加到相位累加器中，相位累加器中的数据输出作为查找地址对正弦查找表进行查找，将相位累加器中的相位信息映射成数字振幅信息[9]。通过D/A转换将数字波形转换为相应的阶梯波，最后经过低通滤波进行平滑处理。数字频率合成器的输出频率精度非常高，具有较高的分辨率，可以快速实现频率的切换，并且在改变时能够保持相位的连续。

图3 数字频率合成器结构

数字频率合成器的输出频率可描述为

(3)

K为频率控制字；N为频率控制字二进制的位数；fclk为时钟信号频率，可达到GHz量级；fo为输出频率。数字合成器输出频率的相对带宽较宽，理论上能达到50%fclk，考虑到对输出杂散的抑制，带宽仍能达到40%fclk。

1.3 系统控制算法

自抗扰控制系统结构如图4所示，其主要由安排过渡过程、扩张状态观测器、非线性组合和扰动补偿等4个部分组合而成。其中,扰动估计与补偿能力最为关键。

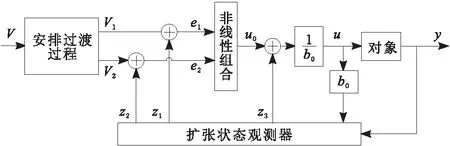
图4 自抗扰控制系统结构

首先对于控制对象，即数字频率合成器进行建模，假定无初始相位，相位累加器中的对应相位为频率控制字的积分。那么可以很容易得到

(4)

x1为相位累加器中相应的相位；x2为x1的导数；u为输入的频率控制字。由于经典自抗扰算法被控对象为二阶模型，针对锁相跟踪系统进行改进后，自抗扰控制算法如下。

安排过渡过程为

(5)

扩张状态观测器为

(6)

非线性组合为

(7)

拢动补偿形成控制量为

(8)

v1为快速无超调地跟上输入信号；v2为v1的导数；z1为经过扩张状态器后的输出估计；z2为z1的导数；z3为系统的扰动估计；e1、e2为系统误差；u0为初始控制量；r0、β01、β02、β03、r、c、h1、b0控制器的参数。最速综合函数fhan(x1,x2,r,h)的具体表达式为

(9)

fal(x,a,δ)具体表达式为

(10)

fal函数是一种非线性函数,是扩张状态观测器(ESO)的核心部分。

2 仿真研究

2.1 参数整定

仿真实验中参考信号为50 Hz，即314 rad/s的正弦波。二阶广义积分中的k值选取0.7，数字频率合成器的时钟为100 MHz，相位累加器中二进制位数为30位。

自抗扰控制器扩张状态观测器参数为：β01=300,β02=4 000,β03=20 000,h1=0.03,h=0.001,c=0.015,r=3 000,r0=900,b0=0.585 2[10]。利用MATLAB/Simulink搭建仿真，参考信号经过二阶广义积分输出2个信号，分别代入复数的实部和虚部计算出参考信号的相位，经过aperiodic模块非周期化。参考信号和控制信号的相位输入到ADRC模块中，经过自抗扰控制算法处理后输出DDS的频率控制字。控制字和相位的关系为

(11)

φ为累计相位；K为频率控制字；fclk为DDS时钟频率；N为相位累加器中的二进制位数。最后该仿真系统输出参考信号，控制信号的波形和两者的幅值差。

2.2 仿真结果

在未加干扰的情况下，仿真结果分别如图5和图6所示

图5 参考信号与控制信号时域比较

图6 未加干扰下的相位误差

仿真结果表明，控制信号与参考信号在0.01 s时基本重合，在0.07s后，相位误差在-2.254×10-4～3.371×10-4之间波动。

在自抗扰控制系统的输出加入幅值为5，频率为1 000 Hz的方波干扰后，得到如图7所示的仿真结果。

图7 干扰下的相位误差

在0.07 s之后，控制信号与参考信号的相位误差在-6.314×10-4～1.637×10-4之间波动。可见，该系统在输出端存在幅值为5，频率为1 000 Hz的方波干扰时，依然能将误差精度控制在10-4数量级。

基于ARM内核的单片机可实现二阶广义积分、非周期化和自抗扰算法，而FPGA实现DDS。参考信号经过高速AD芯片采样进入单片机，单片机输出频率控制字给DDS，同时DDS反馈输出信号的相位信息给单片机。此硬件方案预计能达到和仿真一样的效果。

3 结束语

本文提出并设计了一种自抗扰锁相跟踪系统，利用二阶广义积分对参考信号进行滤波并正交化，通过复数运算得到实时相位。运用改进的自抗扰控制算法控制DDS的频率控制字。通过Simulink仿真可知，在有较大高频方波的干扰下，误差精度保持在10-4数量级，并且相位累加器的二进制位数越大，误差精度还能进一步提高。在抗干扰方面，该控制器具有很强的鲁棒性和抗干扰能力，能够有效地抑制不确定负荷扰动的影响，对理论研究和工程应用具有一定的参考价值。