面齿轮磨削力建模与工艺影响分析
李 湾,李学坤,明 瑞,罗 旦,刘海渔,明兴祖
(1.湖南汽车工程职业学院,湖南 株洲 412000;2.湖南工业大学机械工程学院,湖南 株洲 412007)
0 引言
面齿轮在机械传动中有着非常优良的特性,能够承受较大载荷,具有紧凑结构的同时还能更好地对传动进行分流,在航空传动领域被广泛使用[1-2]。精加工过程中提升面齿轮的精度有许多工艺,磨削过程在众多工艺上非常重要,直接决定最终的精度等级。在对面齿轮进行磨削时,会产生能量消耗等影响,主要表现为磨削时发生摩擦产生的热量,同时振动也会降低加工精度。造成这些现象的主要原因就是磨削力。磨削力是评价工件材料耐磨性以及砂轮锋利程度的一个重要指标[3],对于面齿轮表面加工精度、磨砂轮的耐用程度等都是直接影响。因此,为了提升表面加工精度,开展了面齿轮磨削力的研究。面齿轮进行磨削的工序中,磨削量的多少对于表面磨削质量有直接影响,磨削砂轮上的磨粒对面齿轮的综合作用以及砂轮耐用度等因素会影响磨削最终的加工精度。对面齿轮磨削力的研究有利于提升齿轮精度,为改变传动磨削方式提供一种新的方法。
Simanchar等[4]提出了一种磨削力模型,并研究了解析模型与等离子喷涂陶瓷涂层精加工过程中获得的实验磨削力之间的相关性。特温特大学研究了摩擦学中各向异性非均质材料的接触,这给面齿轮磨削加工过程带来的表面残余应力处理方法提供了新的思路。萨班奇大学的学者基于个体沙粒相互作用的分析研究了磨削力模型,此模型在很大程度上改良了砂轮磨削时有用工作磨粒的数目。Shimada等[5]不计摩擦力的影响,分析计算得出了当振幅增长和砂轮速率的减小时,磨削力的下降率呈增大趋势的结论。刘晓雯等[6]在砂带磨削原理的基础上对民用航天发动机涡轮叶片进行改良,采用离线模拟以及实验数据统计等方法验证了所选加工工艺参数的合理性。王会良等[7]基于传统平面磨削力的数学模型,在成形法磨齿的基础上建立了新的磨削力模型,并验证了改良模型的有效性。罗勇等[8]通过大型齿圈在磨削时的磨削余量对磨削力的影响,基于磨削接触区域模型等建立了磨齿余量模型,提高了齿圈成形磨削的加工精度。文献[9]对螺旋锥齿轮磨削力的影响因素进行探索,其推导的磨削力计算公式在物理意义上可用于面齿轮中,并给出了一种精确的计算方法。面齿轮在机械加工中应用广泛,在工业方面以其优异的性能受到许多学者研究,在其磨削原理以及装配方面都取得了一定的成绩,但对于以磨削力作为特征参数建立磨削模型的研究还未有较先进的报道。
本文以蝶形砂轮加工面齿轮为题,研究磨削过程中砂轮磨粒对齿面的磨削原理。将蝶形砂轮划分为单颗粒磨粒,建立数学模型。分析磨齿过程中磨削参数与磨削力之间的关系,同时分析磨削用量对磨削力的影响规律[10-11]。
1 面齿轮磨齿原理
正交面齿轮的磨削原理如图1所示。选用蝶形砂轮磨削,在不同位置的蝶形砂轮代表了随着时间变化砂轮的磨削动态。蝶形砂轮齿形为渐开线,其轴截面齿廓修整成虚拟小齿轮的断面齿廓,随机在任一加工位置处砂轮形成线接触的小齿轮是虚拟不存在的,这个虚拟小齿轮与面齿轮之间以1个点作为接触,2条接触线的交点为接触点。在加工过程中,砂轮高速转动切削面齿轮的同时又绕假想小轮轴线做旋摆(即延迟改变碟形砂轮的安装角φB),面齿轮依照预设传动比绕本身轴线转动实现展成运动。

图1 面齿轮磨削原理
磨削齿面包络方式如图2所示。为了实现使面齿轮齿面被完整包络,可按如下形式完成[9]:机床上B轴角度(图1中φB),固定在初始位置上,此时所处的位置可看作蝶形砂轮在虚拟齿轮齿面上,工作时,蝶形砂轮保持匀速状态在面齿轮齿宽方向上磨削;完成后改变安装角φB,重复上述研磨过程,再次在面齿轮齿宽方向上进行研磨,2次磨削过程完成后,这样形成的面齿轮齿面在齿廓方向上是由一些倾斜的凹曲面磨削轨迹(图2中Σ1和Σ2)包络构成。此工序在研磨过程中是对每一个单齿分别磨削均匀分度,重复进行研磨,保证所有齿的磨削完成。
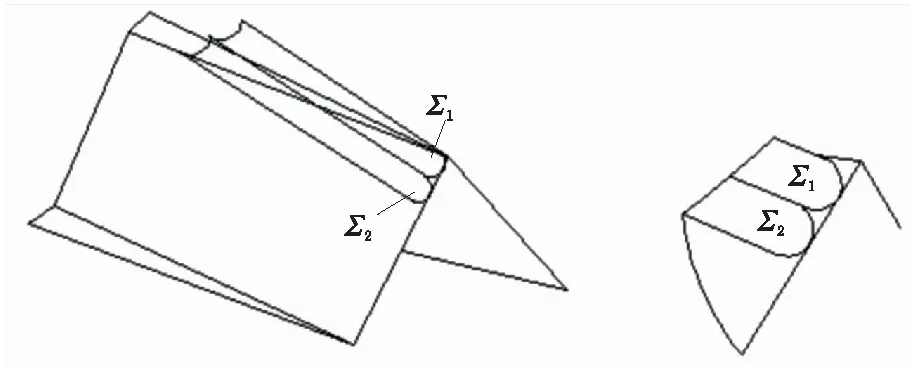
图2 磨削齿面包络方式
2 面齿轮磨削力特征参数的数学模型
磨削加工面齿轮的过程中,磨削下来的金属碎屑和磨削产生的磨削热会严重影响加工出来的面齿轮精度。磨削碎屑的颗粒极小,在使用蝶形砂轮磨削面齿轮的过程中,该颗粒无法随着工件与砂轮的运动被带出材料表面,会附着在两者中间,随着碎屑堆积,减少了磨粒与面齿轮的有效接触,从而磨削力随之降低,其中较大的颗粒在磨削过程中会刮花面齿轮表面,进一步的提高磨削难度;同时,磨削热的产生使面齿轮表面受到热应力的影响,在磨削过程中降低材料耐磨程度,需要通过建立磨削力的数学模型,得到一个合理的磨削力,来减小磨削热对磨削带来的影响。
影响磨削力的主要因素为磨削用量以及进给量,其中进给量的大小可以通过砂轮磨削时的有效磨粒数以及磨粒的切削深度来决定,控制进给量来调整磨削力的大小不能有效降低磨削难度;同时在磨削时磨削宽度、弧长也在很大水平上影响磨削力,从而加大磨削难度。
2.1 磨削接触弧长与接触宽度
由Gleason接触原理可知,触及点的磨削力构成的瞬时触及范围是椭圆,如图3所示,磨削点为该椭圆正中间,磨削触及点弧长为椭圆长轴,磨削触及点宽度为椭圆短轴,椭圆的面积即为触及处的面积。图3中坐标轴Σ、η为公切面上2个坐标轴,用以确定瞬时接触椭圆;ρ1、ρ2为主方向矢量;σ为主方向ρ1与坐标轴η的夹角;αs为主方向之间的夹角[12]。瞬时接触椭圆长轴lk、短轴b的计算公式为[13]

图3 磨削接触椭圆
(1)
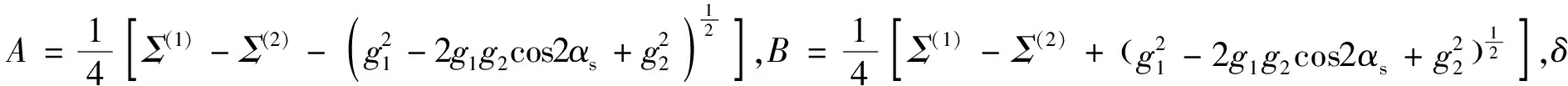
2.2 砂轮单位面积有效磨粒数
在磨削加工过程中,砂轮上的磨粒一部分不参与磨削,需要计算经过磨削弧区中有效的参与磨粒数。砂轮单位面积有效磨粒数的计算公式[14]为
(2)
f为参与磨削的磨粒百分比,一般取50%;v为砂轮磨粒的体积分数,一般取0.240;dg为磨粒当量球直径,dg=M/15.2,M为磨粒粒度。
2.3 磨粒的平均切削深度
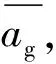
(3)
vw为工件进给速度;vs为砂轮速度;ap为砂轮磨削深度;N为砂轮单位面积有效磨粒数;lk为磨削接触弧长。
3 面齿轮磨削力模型
砂轮磨削面齿轮主要体现为砂轮磨粒在工件表面滑擦、耕犁和切屑打磨。磨削力的产生则是由上述3种过程所带来的物理现象。这3种过程都会产生对应的力,其中耕犁力相对较小,可忽略不计。然后将磨削力在空间中分解为切向与法向上的磨削力Ft与Fn以及纵向磨削分力Fa,由于Fa较小,在建模过程中忽略不计[9]。面齿轮齿面为曲面,在分析磨削力时各点的曲率有所不同,使用蝶形砂轮磨削面齿轮时,各种运动在分析磨削力时会增加分析过程。
根据一些现有的研究可知,面齿轮齿面上各点处的曲率较小(0.020 mm-1以下),利用有限元分析法将其转化等效为平面考虑,不影响模型准确性[16]。分度运动产生的力在磨削过程可以不计,因其不产生磨削力。
如图1和图2所示,面齿轮齿面的磨削轨迹为Σ1或Σ2时,机床B轴处于静止状态,此时B轴不发生转动,磨削过程不产生运动来影响磨削力;当B轴开始转动时,面齿轮的自转与其共同形成了展成运动,砂轮的磨削状态发生改变,磨削轨迹由Σ1向Σ2开始转化。由上述过程分析可以知道,展成运动在齿轮齿面上磨削轨迹形成时,磨削力不会因为展成运动而发生变化。面齿轮磨削力的求解过程中,展成运动是由刀具与工件一同旋转组成的复合运动,该过程产生的力不参与磨削力的复合;磨削过程中的分度运动是由给定的角度或长度间隔所进行的运动,在1个周期内不产生参与磨削的力,由上述分析可将面齿轮磨削时的瞬时接触齿面作为等效平面来对磨削力进行求解。
面齿轮齿面是一个不规则的曲面,其上各点曲率不同,每点的力也尽不相同,在分析磨削力时,需要考虑的分力太多,会加大对磨削力分析的困难。面齿轮磨削过程中的切削运动、进给运动以及其他的各种运动,在分析磨削力时忽略不计,而后以等效平面来分析研究[17]。将各种运动合成分解后,可以减少在等效平面上分析磨削力的求解过程,但是不影响磨削力的精度大小。法向磨削力Ft在磨削过程中起主要磨削作用,磨削过程中磨粒磨齿面之间在该力的作用下发生滑擦,齿面打磨过程中落下的部分磨屑未能及时清理的情况下会参与到磨削过程,由于磨屑颗粒较小,堆积后会对齿面形成保护层,减少磨粒的有效参与数,降低磨削效率。在建立模型时,需考虑该力带来的影响[12]。
在建立面齿轮的磨削模型时,磨削接触为瞬时接触,需要考虑齿轮压力角的存在。在保证模型准确的前提下,磨削面等效为平面。根据Guo的倾斜面磨削理论[18],面齿轮磨削等效模型如图4所示。图4中,ap为砂轮径向磨削深度;α为被磨处齿轮压力角;磨削区砂轮磨削宽度b上任意点沿α余角方向(β角)的投影截面上等效接触形状为椭圆形,磨削深度ap变化为apsinα。磨削力的大小可由参与磨削的磨粒总数与磨削过程中独立的磨粒受力之积来确定[12]。
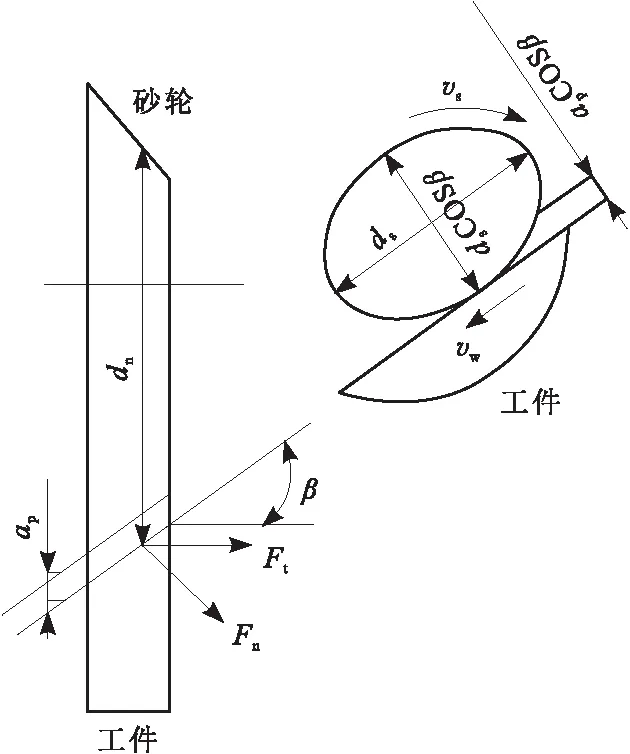
图4 面齿轮磨削等效模型
3.1 单颗磨粒滑擦力模型
砂轮上的磨粒在磨削面齿轮时的进度可分为滑擦、刻划以及最后的切削等过程。在磨削滑擦过程中,蝶形砂轮的切削刃与面齿轮表面发生接触,齿面受到的轻微弹性变形忽略不计,其中微切削刃在磨削过程不起作用。根据张建华等[19]建立的单颗磨粒滑擦力Fh计算模型为
(4)
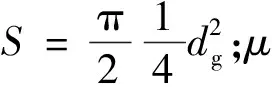
3.2 单颗磨粒成屑力模型
影响磨削力的主要因素是磨削过程中磨粒的参与数量以及进给深度。建立单颗磨粒的成屑力模型,以锥形磨粒设立模型,其顶角为2θ,该模型的建立简化了磨削力的分析步骤。单颗磨粒成屑切削受力情况如图5所示。磨削开始时有效磨粒参与磨削切入材料表层,成屑力dFg对于圆锥面有一个反向作用力,分布范围如图5a中箭头范围所示。由图5b能够得到,dFg分解成水平方向上的成屑分力dFtg与垂直方面上的法向成屑分力dFng,磨粒圆锥体顶尖上的面积dA(如图5c阴影部分)上的的成屑力dFg为

图5 单颗磨粒成屑切削受力示意
dFg=FpdAcosθcosφ
(5)
Fp为单位磨削力;dA为切削力dFg作用于圆锥面上的微小面积;φ为切削力dFg与磨削方向的夹角。
设磨粒母线与工件接触的长度为ρ,则dA为
(6)
在圆锥面上单颗磨粒所受的水平成屑分力dFtg和垂直方向成屑分力dFng为
(7)
单个磨粒受到的水平成屑分力和垂直方向成屑分力为[7]:
(8)
对面齿轮磨削时,单位切削面积上切削力为单位磨削力Fp为[20]
(9)
ξ为无量纲指数,其取值范围ξ∈(0.500,0.900);σ0为单位磨削力常数,与工件材料有关。
3.3 面齿轮磨削力数学模型
蝶形砂轮上参与磨削的磨粒磨削产生的滑擦力与磨削过程的成屑力,二力合并分解得到面齿轮磨削力的数学模型为
(10)
Ft为切向磨削分力;Fn为法向磨削分力。
4 面齿轮磨削力仿真与实验分析
4.1 磨削力仿真分析
仿真时,磨削设备为五轴联动数控磨床QMK50A,碟形砂轮为D300×25×127 CBN60L5R35,正交面齿轮材料为18Cr2Ni4WA,采用逆式干磨来磨削工件,磨削液采用冷却性能更好的水基磨削液。齿轮齿胚参数如表1所示,结合磨削面齿轮的工艺参数并由式(1)计算得:磨削接触弧长lk=0.463 mm、磨削接触宽度b=0.565 mm。构建蝶形砂轮磨削面齿轮的模型以后,仿真分析观察磨削力如何随着设定的参数改变。磨削过程中基本条件预先设定不变,加工工件的材质、磨削液、砂轮等对磨削影响不大,砂轮转速、磨削用量与面齿轮行进速度等会随其改变直接影响磨削力。根据式(10)所得到在各磨削用量参数下的磨削力仿真值如表2所示。
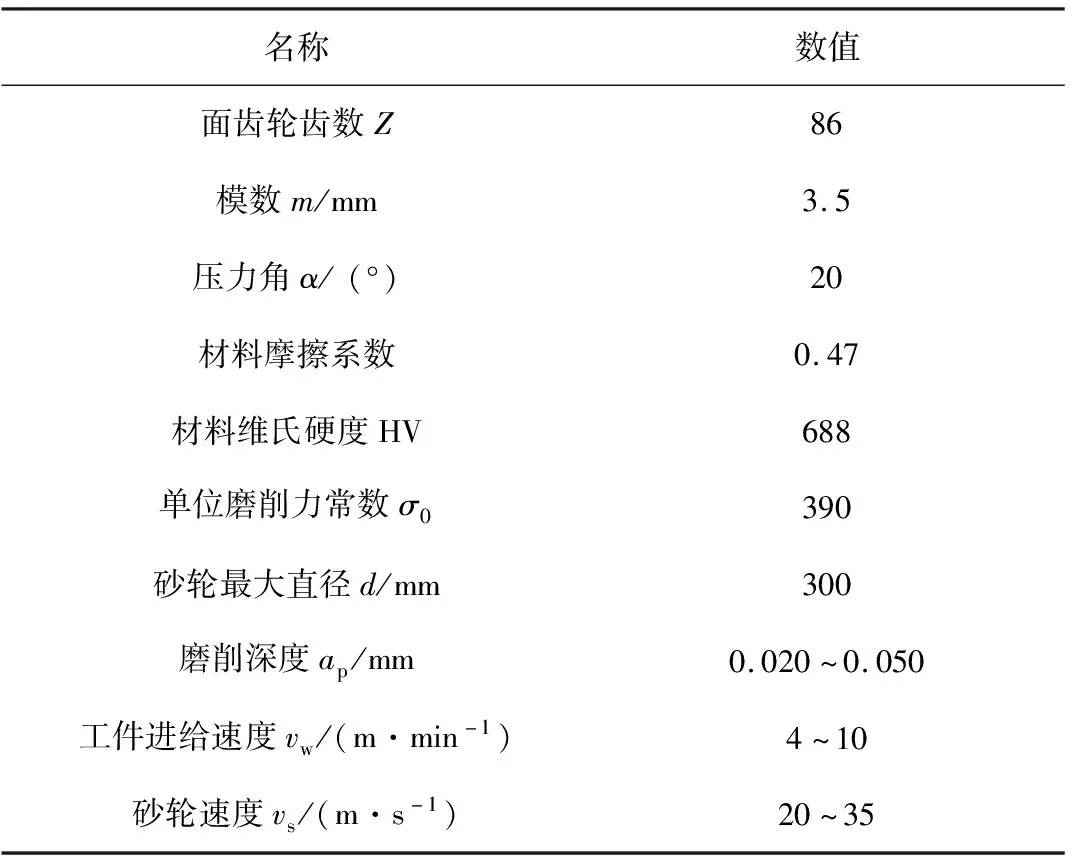
表1 正交面齿轮齿坯参数及磨削工艺参数
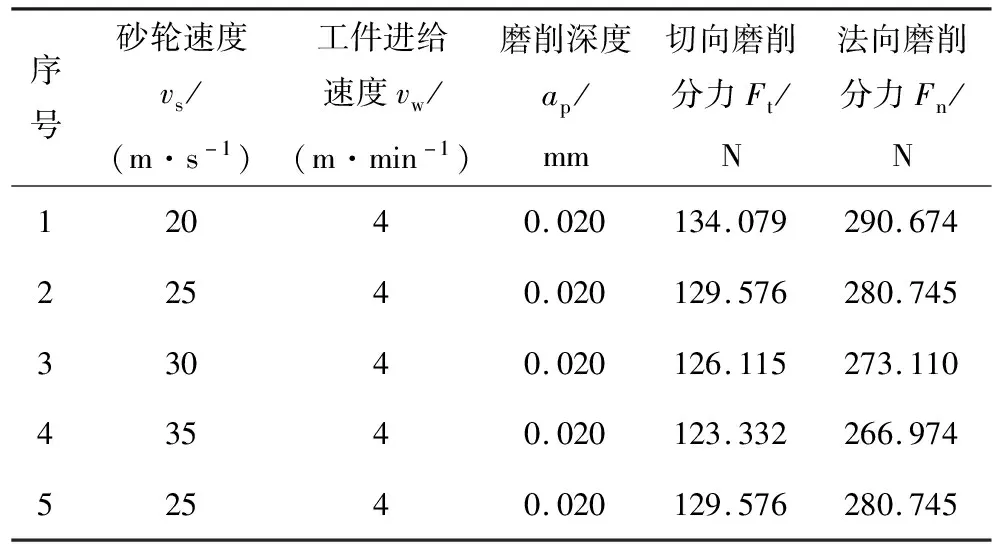
表2 各磨削用量下磨削力仿真值
4.1.1 砂轮速度对磨削力的影响
在工件进给速度为4 m/min、磨削深度为0.020 mm时,砂轮转速取值范围在20~35 m/s时,仿真所得砂轮速度与磨削力关系如图6所示。
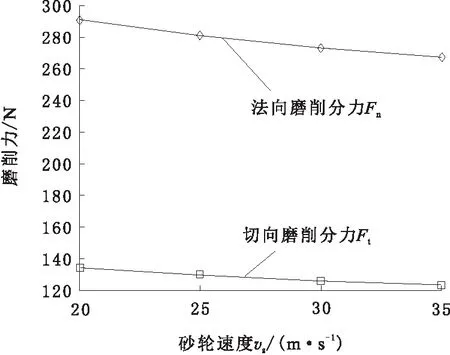
图6 砂轮速度与磨削力的关系
由图6可知,砂轮转速vs从20 m/s增加到30 m/s时,法向磨削分力从290 N降低到270 N,切向磨削分力从138 N降低到122 N。2种分力都降低的原因是当工件进给速度与磨削深度不发生变化时,砂轮转速提高导致单位时间的工作磨粒数参与磨削的磨粒减少,磨削力从而减小。
4.1.2 工件进给速度对磨削力的影响
当蝶形砂轮的转速为25 m/s、磨削深度为0.020 mm时,使用该参数仿真可得工件进给速度为4~10 m/min,仿真所得的工件速度与磨削力关系如图7所示。
由图7可知,工件进给速度vw从4 m/min增加到10 m/min的过程中,切向磨削分力从140 N上升到150 N,法向磨削分力从290 N增加到330 N。

图7 工件进给速度与磨削力的关系
当砂轮转速与进给深度为固定量时,磨粒的切削深度会随着面齿轮进给速率上升而增大,磨削轮上的工作磨粒增多,磨削力在加工时随之增大。
4.1.3 磨削深度对磨削力的影响
当蝶形磨砂轮转速为30 m/s、面齿轮行进速度为6 m/min,磨削深度从0.020 mm增加到0.050 mm时,仿真所得的磨削深度与磨削力的关系如图8所示。
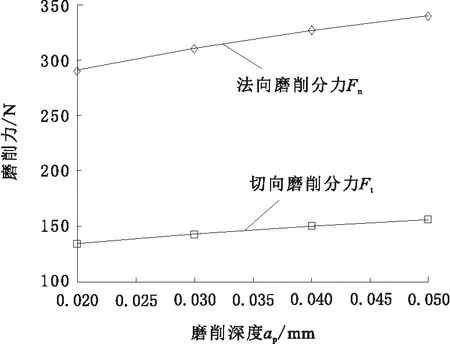
图8 磨削深度与磨削力的关系
由图8可知,当磨削用量增大会使切向磨削分力与法向磨削分力都呈现增大的趋向。磨削深度增加会增多磨削过程的出屑量,此时工件进给速率与砂轮转速不发生变化,多余的磨削去除量增加了磨削时的有效磨粒数,磨削力随着有用磨粒数的增多而变大。
4.2 磨削力实验分析
为提升面齿轮磨削力模型的准确性与契合程度,需多次实验验证,实验过程中各参数与仿真时保持一致,严格控制加工偏差。实验采用的测量磨削力的系统是由多通道信号调节器、可调节式测力仪Kistler9124型和高运算量计算机等组成,如图9所示。通过砂轮上的旋转式测力仪,得到的各磨削进给用量下的磨削力实验结果如表3所示。
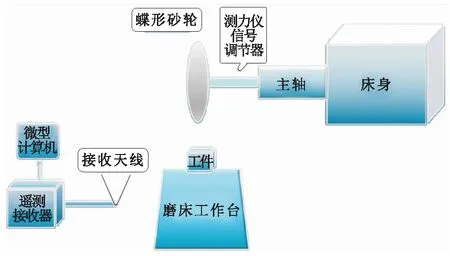
图9 面齿轮磨削力测量系统示意
将表3的实验值与表2中各磨削力仿真值相比较,可看出实验过程中真实磨削进给量对法向磨削分力和切向磨削分力的影响程度与仿真结果高度符合。法向磨削分力的最大相对误差值为17.9%,切向磨削分力的最大相对误差为6.7%,该误差值在可信范围内,证明了设计的面蝶形砂轮磨削面齿轮齿轮的磨削力模型是合理可靠的,能够充分反映加工过程中磨削力的变化。

表3 各磨削用量下磨削力实验值
5 结束语
本文研究了蝶形砂轮磨削面齿轮时磨削力的变化与磨削规律,建立单颗磨粒的成屑力模型,通过多元合并得到面齿轮磨削力模型。由于面齿轮齿面各点曲率不同造成磨削力分析困难,运用倾斜面磨削理论并采用等效平面转换法,由有用磨粒的滑擦力与成屑变形力的数学公式去分析磨削力的变化程度,得到了主要的变化因素,这为通过改变磨削力的大小来提升加工精度提供了理论依据。
影响面齿轮磨削的主要变量为进给速度vw、磨削深度ap和砂轮的速度vs。砂轮速度的增加减少了磨削过程中的有效磨粒数,降低磨削力。法向磨削分力Fn在磨削参数变化时,其变化率较高。实验验证了面齿轮磨削力模型的可靠性。
面齿轮磨削力模型给出了磨削过程主要变量的变化对磨削参数影响的变化率。该模型在提升面齿轮磨削精度、优化装配工艺和改善加工方式等方面,提供了一定的参考作用。

