新能源主动支撑电网能量获取及调配策略研究
李红刚,王红庆,蒋成博,卢晓光
(1.平高集团有限公司,河南 平顶山 467001;2.许昌许继风电科技有限公司,河南 许昌 461000)
0 引言
新能源风电在发电领域占比逐年增大,且仍将迅猛发展,对电网影响愈发显著[1-3]。电力系统电力电子化特征凸显,电力系统旋转备用容量及转动惯量相对减,导致电力系统安全稳定运行的压力增大[4-5]。为改善风电运行特征,缓解电网运行压力,进行风电虚拟同步机的研究[6-9],以主动支撑电网。本文基于此背景,结合主动支撑项目,进行风电主动支撑过程中的能量调配策略的研究。风力发电机组正常发电状态与电网频率处于解耦状态,没有相互关联[10]。风电虚拟同步机开发即建立电机发电功率输出与电网频率之间的动态关联过程[11-15],利用控制手段在电网波动过程中主动支撑电网平稳运行。风机正常发电时,由风轮吸收能量,经传动链带动发电机转动发电[16-17],这个能量转换传递过程是由实际旋转机构实现的,具有实际惯量特征。而电机输出功率随电网频率波动的主动支撑惯性特征,是由电力电子机构通过控制调配实现的,其本身不具备惯性特征,本文称为风机虚拟旋转轴。本文研究重点的是建立风机虚拟旋转轴与实物旋转轴之间的能量转换联系。通过分析实物旋转轴上的惯量储备及能量吸收转换特点,寻找可利用调频支撑功率特性。另外通过虚拟轴调频特性的改变,研究调频对整机运行的影响。
1 风机实物轴可调频能量分析
风机实物轴可获得的调配能量有风轮吸收的风能和风轮自身的惯性动能[18]。风机吸收风能的效率随叶尖速比和变桨角度的变化而变化,由贝茨理论证明得到,吸收效率最大值不超过0.593。风机吸收效率可通过桨距角调整达到0。利用风机吸收风能叶素动量理论,经数据拟合手段处理,可得风能吸收率与桨距角、叶尖速比拟合关系式为
(1)
β为桨距角;λ为叶尖速比。λi与输入量的函数关系为
(2)
1.1 实物轴变转速储能及可调配能量分析
桨距角为0时,风机吸收风能能力达到最大,此时风能利用系数由式(1)退化为
(3)
风能利用系数也退变为图1的形式。由图1可知,当叶尖速比越过最优尖速比后,风能利用系数会随之降低。故在外在风速不变的假定下,叶尖速比脱离最优点后,风轮的风能吸收率会随之降低。实物轴转速的变化会引起2个方面能量的变化:降低风能利用系数所导致的风能吸收率变化的能量;风轮转速相对于最优转速提高所存储下来的转动惯量。

图1 最佳桨距角下风能利用系数与叶尖速比关系
利用以上2个特点,在设计具有虚拟同步机功能的风机时,牺牲部分正常发电功率,在风机正常运行时适当提高风机轴转速,实现风机提速储能目的。提速控制可由风机转矩控制实现,转矩控制以发电机转速为输入量,控制转矩输出大小,从而改变叶尖速比,进而改变风能利用系数。整个转矩控制依据最优转矩系数k实现,则有
(4)
设定需求叶尖速比λ值,由式(4)可计算出转矩转矩需求k。
记最优发电最优发电叶尖速比为λopt0,提速储能所需控制尖速比为λsto0,则根据式(4)可分别得到最优发电最优发电风能利用系数Cp,opt0,提速储能控制风能利用系数Cp,sto0。测量当前发电功率Psto0,则风机恢复最优发电后,因风能利用系数变化存储的能量为
(5)
测量当前发电机转速记为Vsto0,记最优发电机转速为Vopt0,由式(4)可计算当前运行转矩利用系数ksto0,可得
(6)
同样过程,由式(4)计算最优风能利用系数下的运行转矩利用系数kopt0,并得如下关系式:
(7)
由以上关系式可以确定Vopt0,则因风轮转速变化存储的惯性能增量为
(8)
由提速储能策略所存储起来的能量为ΔPsto与ΔPJ之和。在调频过程中,假设外界风速不变化,ΔPsto是可以持续被利用的能量,而ΔPJ却是只能短暂提供惯性支撑的能量。差别原因是ΔPsto为风轮吸收能力的变化导致的能量变化;而ΔPJ却是风轮提速后存储机械能,在风轮转速变化趋于稳定后,能量随之停止释放。
1.2 桨距角储能及储能能量计算
风机实物轴只能运行在限定的转速范围内,通过实物轴转速变化获得的可调频能量有限。为获得更大的能量调配范围,须利用变桨储能方法来实现。为使式(1)风能利用系数解耦为只与桨距角有关的二维关系,限定如下讨论范围:在任意桨距角下,只讨论风机运行在最佳叶尖速比情况下,不同控制桨距角与最优桨距角之间的风能利用系数差异,进而设计确定工况下的功率预留控制算法。
风机合理运行的尖速比区间为[5,20],桨距角在发电状态下的合理运行区间为[0,40]。在这一限定区间内,对于确定的某一变桨角度,则式(1)是在风机合理运行尖速比区间内的单调函数或只有1个拐点的函数。故此,在上述合理运行区间内Cp有且只有1个峰值,即只有1个最大值。
为计算方便,利用软件计算不同桨距角下在区间[5,20]上的导数为0的点,即可得最优功率和最优功率利用系数。做多个不同桨距角下的最优功率利用系数连线,即可得到最优功率利用系数拟合曲线。
记最优发电风功率利用系数为Cp,opt0,在当前桨距角下的最优发电风功率利用系数为Cp,β,测量当前发电功率Pβ,则风机恢复最优桨距角后,因桨距角变化压制的功率释放量为
(9)
1.3 实物轴三维动态联合储能及能量调配控制实现
机组实际运行中,单纯依靠提速储能方法存储能量有限,不能满足调频储能要求;单独利用变桨控制,在响应调频初期,桨叶未调整到最佳吸收风能位置需要一个过程,因调频响应速度指标限制,风机迅速增发功率,会导致转速迅速降低,当叶片进入最佳吸收风能位置后,因叶尖速比已脱离最优尖速比过多,也无法尽快吸收风能,故此,需要提速控制与变桨储能控制结合应用,达到储能目标。
利用部分提速组合部分桨距角储能的控制方法,功率利用系数Cp和桨距角、叶尖速比之间构成了动态三维关系图。因控制过程是对这种关系的后验跟踪过程,故此无法事前精确限定三者关系。为工程实现需要,根据控制需求限定运行条件,做如下限制规划:确定提速储能能量需求,进而计算出提速储能转矩控制参数,在变桨储能动态变化变桨过程中提速储能参数不再变化。
正常运行时,风机提速储存能量需达到储能要求的5%,以便虚拟机快速响应,此时依据式(5)和式(8),可以反推出风机所需转矩系数ksto0。此控制系数设定为风机转矩控制所需系数,在桨距角变化时不再改变此控制参数。
剩余的能量存储以桨距角脱离0°的方式完成。在桨距角脱离0°过程中,风轮并不能维持在提速储能所需控制尖速比λsto0处,这是因为桨距角的变化会使入流角改变。为实现对三维能量变化的控制,本文利用数学拟合的方法。随桨距角变化功率利用系数在限定区间内是单调函数,利用这一特征,用曲线拟合的方法可以找到预留功率与桨距角之间关系的规律曲线。曲线拟合首先在转速能量调配参数确定的情况下,对桨距角变化及能量储存需求进行拟合。首先是找到储能目标下,当前功率和预留桨距角的多个对应点,然后拟合出整体曲线。在拟合点计算过程中,可以利用式(9)进行计算。本文在拟合过程中利用行业认可的Bladed软件进行快速拟合,Bladed软件可精确反映式(9)物理关系,同时具有快速输出其他有用数据的能力。拟合步骤如下:
a.按设计要求确定提速策略转矩系数ksto0。
b.确定需拟合点恒定输入风速v1,并作为仿真软件Bladed的输入风速。
c.在桨距角为0,转矩系数为ksto0下,仿真输出稳定功率,记为Popt0。
d.确定初始桨距角β1,在转矩系数ksto0控制状态下仿真输出稳定功率,记为Pa1。
e.计算Pa1-Popt0与需求预留功率的差距。
f.利用二分法思维改变桨距角为β2,并重复步骤d-步骤e的操作,使Pan-Popt0与需求预留功率近似相等。
g.重复步骤b-步骤f的操作,找到全功率段足够拟合曲线数量的点。
h.利用拟合点数据,进行多项式拟合,可拟合出风速-功率曲线、叶尖速比变化曲线、桨距角-功率变化曲线等所需控制曲线。
2 实物轴能量支撑虚拟轴调频的实现策略
风机虚拟轴为电网频率与发电功率之间的相关性变化,是利用控制手段模拟同步机的惯性外特性,达到稳定电网的目的。实际策略设计中,从对电网主动支撑角度出发,当电网出现波动后,虚拟轴出力有必要模拟同步机惯性外特性,体现对电网波动的阻尼效果;当电网恢复正常状态过程中,模拟同步机惯性外特性反而不利于电网快速恢复。故此,虚拟轴主动支撑出力策略制定思路为:充分发挥电力电子优势,在电网正常频率过程中模拟同步机惯性外特性,提供电网频率变化的阻尼;在电网恢复正常频率的过程中,发挥电力电子的优势,快速恢复正常出力,使电网能更快速的恢复到正常频率水平。
2.1 风机虚拟轴惯性特征动态支撑参数提取
同步机载荷突变的暂态过程体现惯性特征,机组输出功率会输出瞬时波动来维持功率平衡,即
(10)
PTi为系统内第i台机组机械功率;PGi为系统内第i台机组电磁功率;ΔPL为电网突变负载;PJi为系统内第i台机组动态惯性储能;m为系统机组数。
在进行风机虚拟轴惯性特性模拟时,依据能量的瞬时变化,推导得出风机输出功率与电网频率的关系。
发电机转子动能E(t)可表示为
(11)
J为虚拟转子转动惯量;ω为转子旋转角速度。
电机转子动能P(t)的功率变化率可表示为
(12)
f(t)为电网频率;p为电机极对数。则有
(13)
(14)
由式(14)近似得出频率与功率的对应关系为
(15)
TJ为惯性时间常数;fN为系统额定频率;PN为发电机组额定功率;f为并网点实时频率。
2.2 风机虚拟轴一次调频特性模拟
同步发电机组系统频率变化后,静态特性分析过程如图2所示。

图2 同步发电机组有功功率-频率静态特性
在特性曲线上任取2点a、b,定义机组的静态调差系数为
(16)
式(16)中,变量用标幺值标识,负号表示发电机输出功率的变化和频率的变化符号相反。图2中:fN为电网额定频率标幺值;Pa为对应频率下的同步电机出力标幺值;f1为电网频率滑落标幺值;Pb为对应同步电机调节出力标幺值。为方便计算功率与频率的关系,令Kf为发电机的功率-频率特性系数,其意义为调差系数的倒数,即
(17)
依据式(17)得出风电机组参与电网一次调频支撑能量为
(18)
Kf为有功调频系数;PN为发电机组额定功率;Δf为频率变化值。
2.3 风机实物轴存储能量支撑虚拟轴调频策略规划
电网频率异常的时间占比有限,风机多数时间是处于正常发电状态,因此在满足调频储能情况下,风机控制会考虑尽量少地预留储备能量,风机在调频中会设置能量支撑上限,本策略设置为10%PN。风机在实现虚拟同步功能时,将虚拟同步控制嵌入风机的正常控制策略之中。风机调频有惯性策略、一次调频策略。融入调频控制后的风机控制策略规划如图3所示,并对图3的策略重要步骤进行逐条解释。
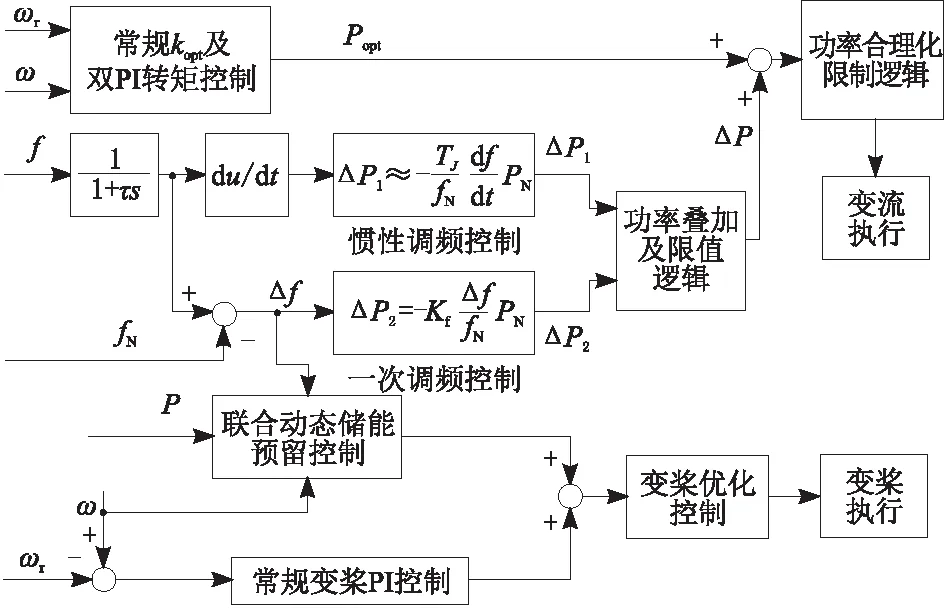
图3 风电虚拟同步控制结构
2.3.1 惯性调频响应策略
惯性调频控制中输入量为电网频率的变化率,依据式(12)计算惯性调频所需支撑功率,并与风机实时功率进行叠加,计算出功率调节目标值。因风机自身物理特性限制,风机实发功率大于20%PN,且电网频率变化超过0.03 Hz时,惯性调频才起作用,其中因备用能量限制,增发功率ΔP限值范围为-10%PN~+10%PN。其中,TJ的选取是策略制定的重要工作,选取越大对电网支撑能力越强,但是过大会导致风机因调阶过大而引起电磁振荡、支撑时间缩短、风机提前退出支撑过程等问题。因此合适的参数对策略的实现尤为重要,目前用测试聚类分析手段获得参数合理值在5附近较合适。
2.3.2 一次调频控制策略
一次调频输入量为电网频率变化量,由式(14)计算获得一次调频有功增发目标值。同样一次调频对电网进行支撑的条件为:风机实发功率大于20%PN,且电网频率变化超过0.03 Hz,其中因备用能量限制,增发功率ΔP限值范围为-20%PN~+10%PN。考虑到备用能量有限及一次调频支撑力度最大化需要,经试验分析Kf值在20附近较合适。
2.3.3 联合动态储能预留控制
风机备用预留方法依据1.3节所述方法进行实现,备用能量预留时刻按照机组额定功率的10%进行计算。针对具体机型,风机在变桨储能实现过程中依据“桨距角-功率”关系,仿真、拟合储能曲线,固化在控制策略中,使风机在运行状态下依靠对桨距角的调节时刻保留10%PN功率备用,在需要功率向上支撑时进行释放。
2.3.4 功率叠加及限制控制
考虑到实际运行时风速的波动,在功率进行支撑过程中,为了稳定功率输出,会出现超过机组运行极限工况,需设定“功率-转速”保护限值,不同机型需根据仿真、计算结果进行保护曲线规划。当超过保护限值后,系统即刻退出有功调频功能,切换至正常转矩控制。
3 实验验证及指标分析
实验时,将完整的虚拟机能量调配策略运行在风机主控制器中,能量调配策略曲线依据不同机型的叶片翼型数据及运行转速区间确定,主控制器完成计算后得到转矩需求指令,下发给变流器执行。虚拟机能量调配策略适用于所有风机类型,因叶片翼型差异导致的机型差异,体现在能量调配策略拟合曲线的差异上;因双馈、全功率变流等变流器差异导致的机型差异,体现在转速-转矩对应关系变比差异上,策略上并无差异。
仿真实验及现场实验选用2 MW双馈机型进行,仿真工具选用行业认可的Bladed软件辅助。仿真除进行必要的参数选取与曲线拟合外,同时验证调频过程对整机载荷的影响;现场实验主要验证调频特性的调频效果和调频指标参数。为验证精确预留200 kW备用调频能量算法的预留准确性,进行了实验,结果如图4所示。由图4可知,预留能量释放后,功率增加值与目标值差值在3%以内。图5为一次调频功率向上支撑工况的实验数据曲线,由于支撑有功已经大于截止功率200 kW,故调频功率按照最大支撑功率输出。从数据上看,一次调频启动时间在2 s以内,上升时间在1 s以内。完全能够达到常规能源一次调频指标要求。图6为惯性调频响应数据曲线图。惯性调频要求响应时间和上升时间较苛刻,从高频率采样数据统计可知,惯性调频的响应时间从控制器辨识到频率加速度再到功率响应的时间为200 ms,加上控制器的频率辨识过程,总响应时间在500 ms以内,可以满足常规能源惯性调频响应指标。
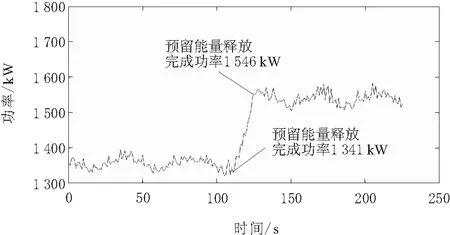
图4 储能释放前后功率风机功率变化

图5 惯性调频功率支撑
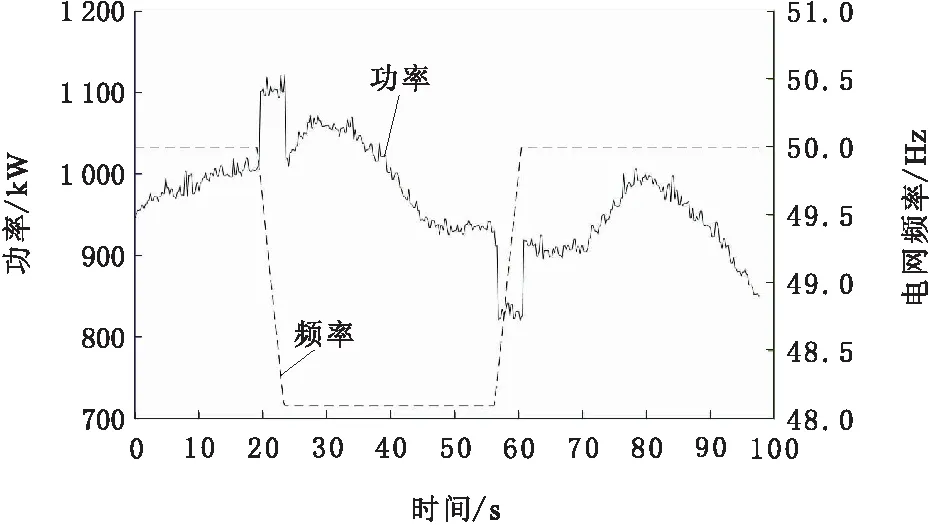
图6 一次调频有功支撑
图7为进行惯性调频过程中,功率支撑达到200 kW工况下的风机振动加速度峰峰值数据。振动峰峰值能侧面反映风机在冲击过程中主要载荷部件的受力变化情况。由图7数据显示:调频过程左右振动峰峰值略有增加,但增加幅度几乎可以忽略,对风机载荷影响不大;调频过程中前后振动峰峰值最大值达到0.65 m/s2,对比本机型1.10 m/s2振动停机保护值,还有较大余量。调频对风机载荷冲击,在不叠加其他故障停机工况时,完全在风机极限载荷的包络之内,对风机极限载荷没有影响。因电网故障发生次数有限,对风机疲劳载荷影响也几乎可以忽略。

图7 调频过程风机振动情况
4 结束语
本文从风机吸收风能的基本理论和风机运行物理特性出发,研究风机叶轮储能即可用能量特性,得到了风机风轮惯性储能量化公式及其用于支撑电网调频能量的计算公式;实现了利用变桨手段进行能量调配用于支撑电网调频能量的计算方法。进而得到了风机动态联合储能及能量调配控制实现策略。
在利用联合储能能量进行电网支撑策略研究过程中,得到了风机模拟虚拟同步机的实现策略,完成了电网支撑策略融入正常风机控制策略的结构设计。风机主动支撑电网调频策略通过了仿真软件的验证及评估;并通过了现场实验进行的调频指标评估。实验结果表明,风机备用能量预留准确,风机主动支撑电网调频指标在合理范围内,风机虚拟同步机控制能实现电网主动支撑。

