一类图的优美标号与序列标号
徐美进,刘春峰,高 洋
一类图的优美标号与序列标号
徐美进1,刘春峰2,高 洋3
(1.辽宁工业大学 理学院,辽宁 锦州 121001;2.中国人民政治协商会议辽宁省锦州市委员会,辽宁 锦州 121001;3.沈阳城市建设学院 基础教研部,辽宁 沈阳 110167)
研究了图的标号问题,通过图的运算以及关联关系构造出一个新的图类P()(),利用函数对应关系给出了该类图P()()对应的优美标号和序列标号,并分多种情况加以讨论说明,从而证明了该类图是优美图和序列图。
优美图;序列图;顶点标号
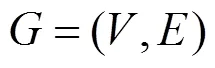
1 预备知识



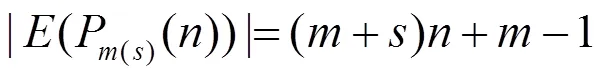
图P(s)()如图1所示。
图1 图Pm(s)(n)
2 定理及证明
证明 分两种情况证明定理1。
情况1≡0(mod2)
定义图P(s)()的顶点标号如式(1)所示。
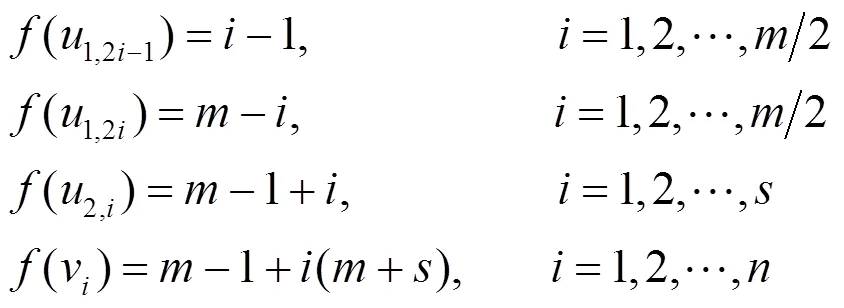
下面验证是图P(s)()的优美标号。
(1)图P(s)()中不同的点,其标号不同。设
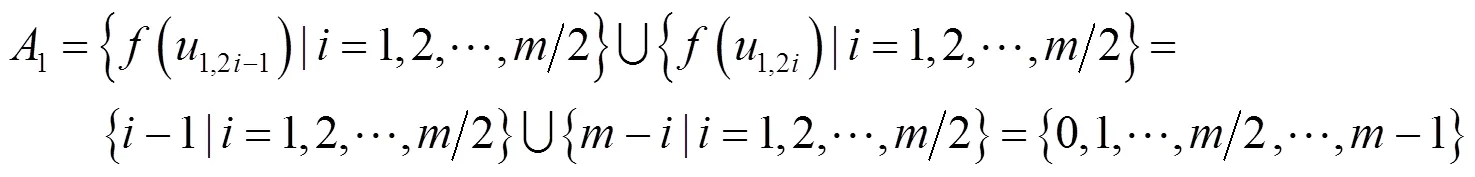
(2)最大最小为
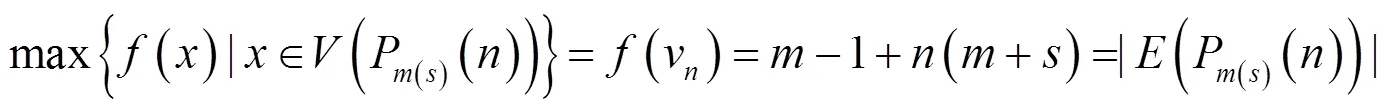
(3)图P(s)()中若边不同,则其标号不同。
由(1)式,有

假设
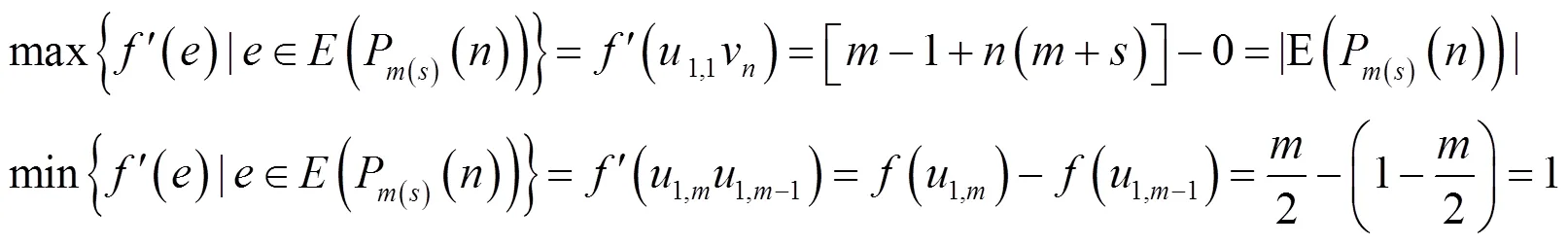
由上述可知是图P(s)()的一个优美标号,图P(s)()是优美图。
情况2≡1(mod2)
定义图P(s)()的顶点标号如式(2)所示。
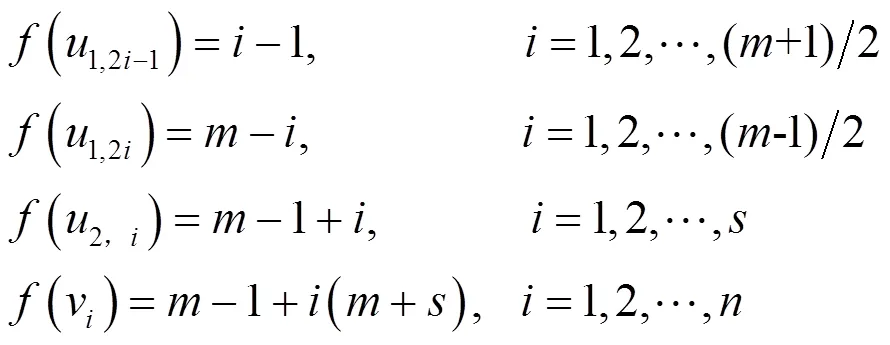
在情况2中,可与情况1同样验证是图P(s)()的一个优美标号,图P(s)()是优美图。
定理1证毕。
图2和图3给出了图3(2)(4)和图4(2)(3)的优美标号。
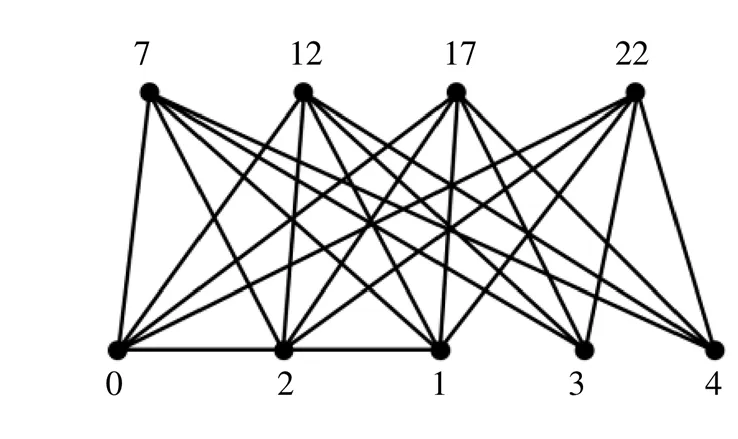
图2 图P3(2)(4)的优美标号
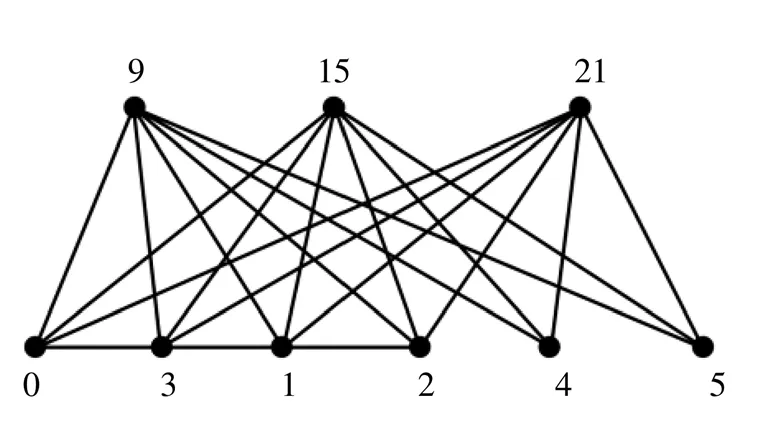
图3 图P4(2)(3)的优美标号
定理2 若(>1)、和是正整数,则图P(s)()是序列图。
证明 分两种情况证明定理2。
情况1≡0(mod2)

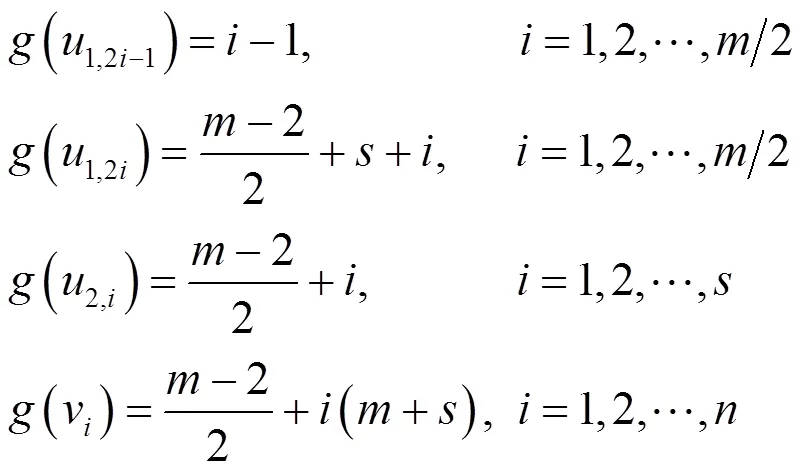
(1)图P(s)()中若点不同,其则标号亦不相同。设
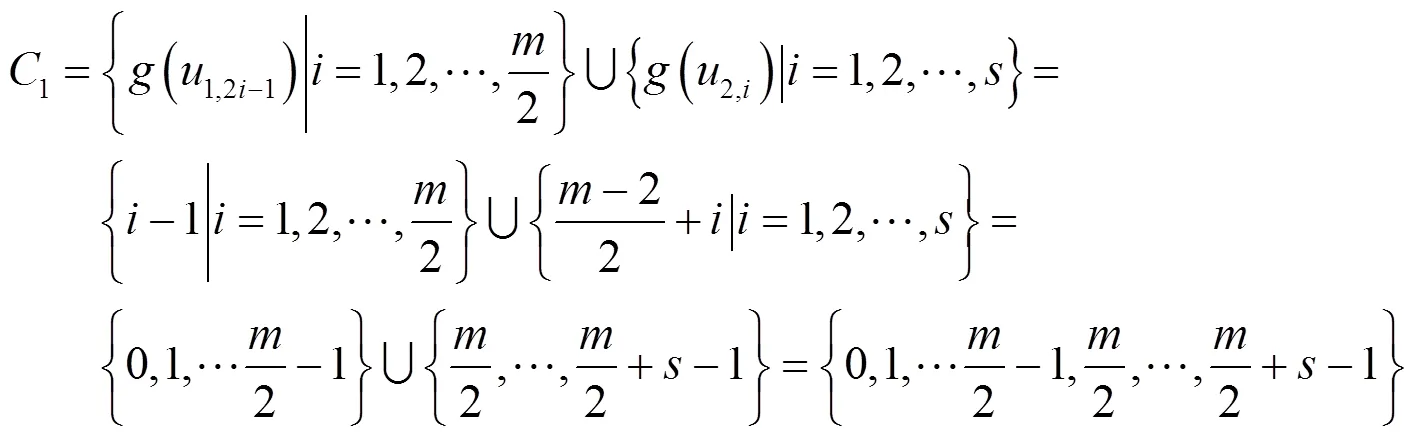
(3)图P(s)()中若边不同,其则标号亦不相同。
根据式(3),有

假设
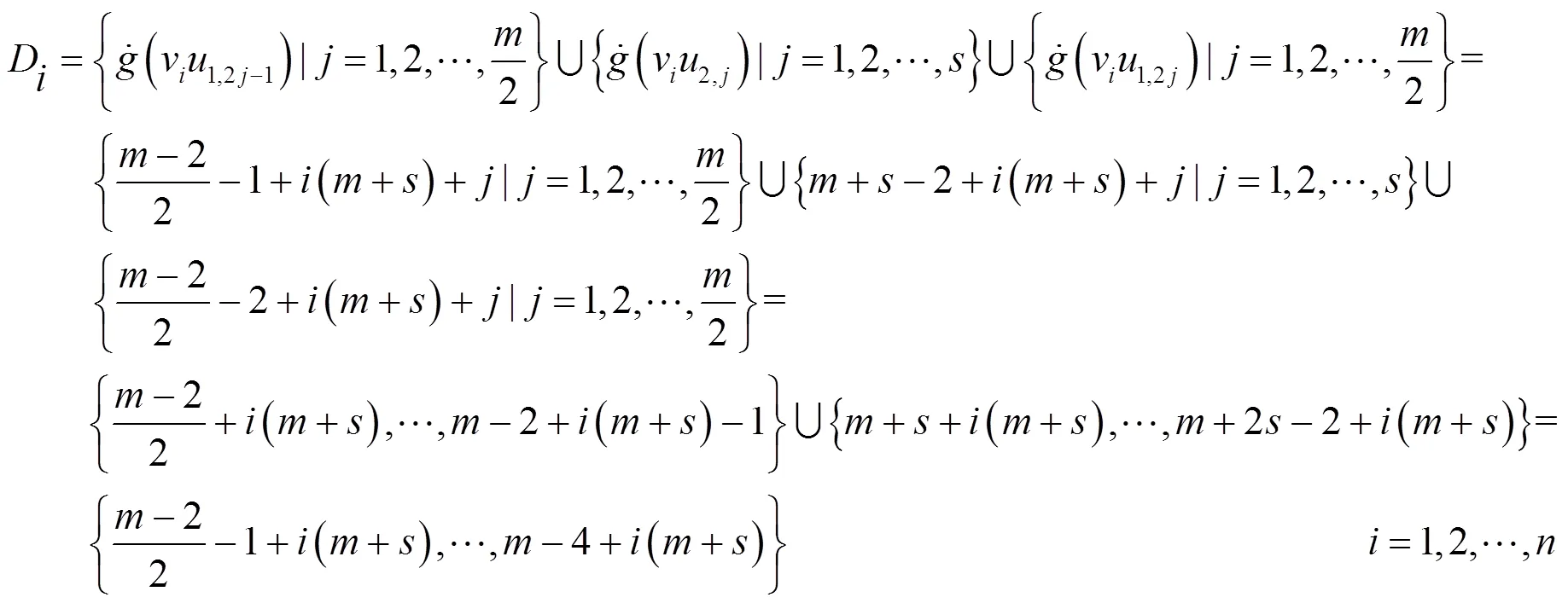
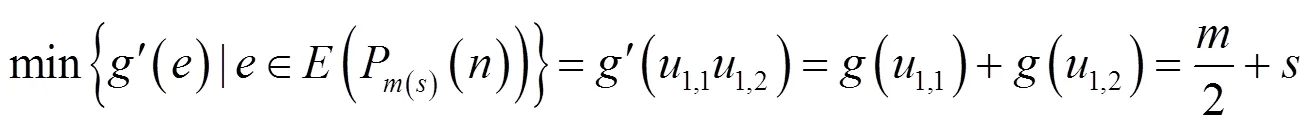
于是,有
由上述可知是图P(s)()的一个序列标号,图P(s)()是序列图。
情况2≡1(mod2)

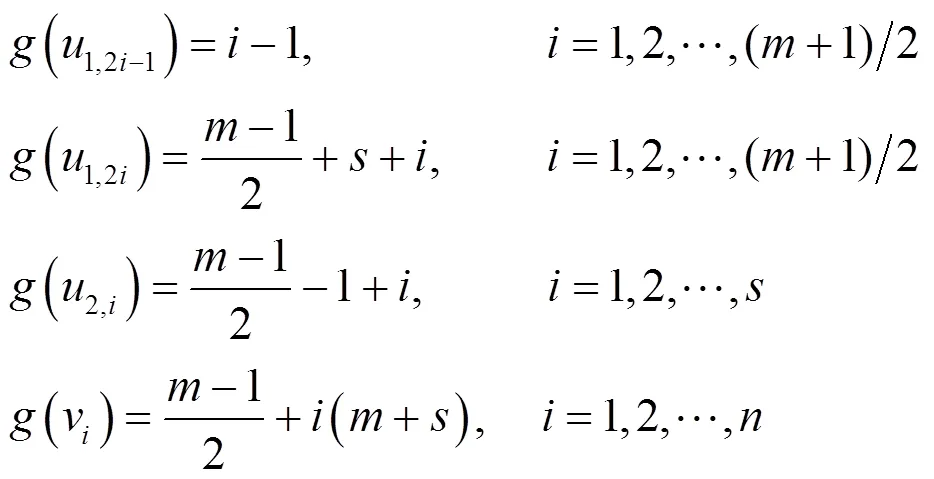
在情况2中,可与情况1同样验证是图P(s)()的一个序列标号,图P(s)()是序列图。
定理2证毕。
图4和图5给出了图4(1)(4)和2(3)(3)图的序列标号。
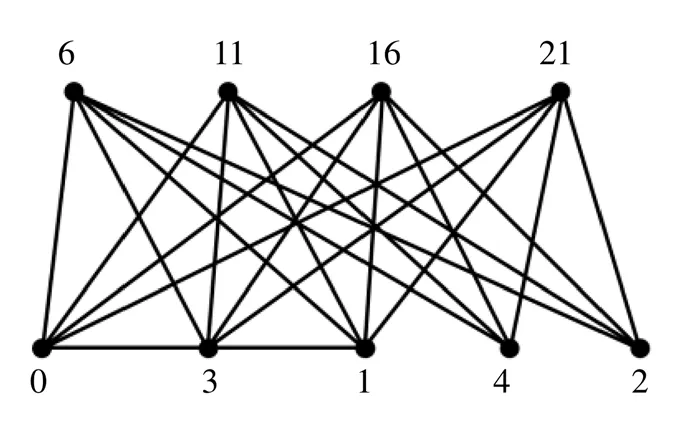
图4 图P4(1)(4)的序列标号
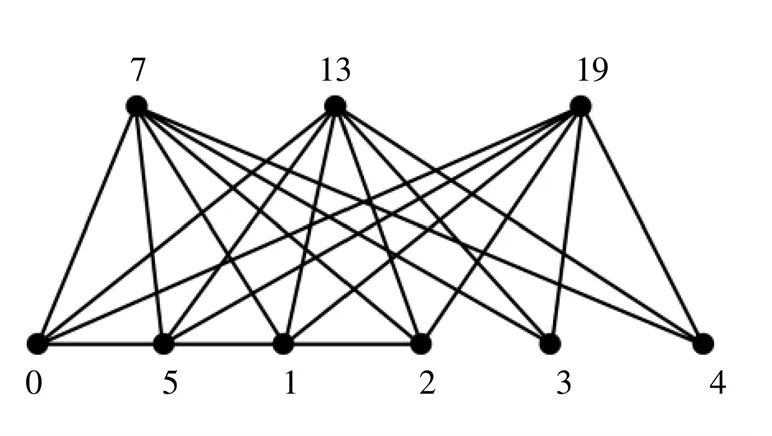
图5 图P2(3)(3)的序列标号
由定理1及定理2,有如下推论。
推论1[10]完全二分图K,n是优美图。
推论2[10]路、星图和扇图是优美图和序列图。
推论3 若(>1)、和是正整数,则图P(s)()是调和图。
3 结束语
本文讨论了图的优美标号及序列标号问题。通过图的运算关系构造出一类新的图P(s)(),给出其具体的优美标号及序列标号,并给出严格证明。
[1] RINGEL G. Problem 25 in theory of Graph of Graph and its application[C]. Smolenice : Proc. Symposium Smolenice, 1963: 162-167.
[2] ROSA A. On certain Valuations of the Vertices of graphs[J]. Theory of Graphs, 1966, 7(3): 349-355.
[3] GOLOMB S W. How to Numbe a Graph[M]. New York: Graph Theory and Computing, Academic Press, 1972.
[4]GALLIAN J A. A dynamic surverv of graph labeling[J]. The electronic journal of combinatorics, 2013, 16: 33-69.
[5] 梁怀学, 刘春峰. 关于图的K-优美性[J]. 东北师大学报, 1991, 23(1): 41-44.
[6] 刘春峰, 赵连昌.重四角鲜人掌图的优美性和序列性[J]. 吉林师范大学学报, 2006, 27(2): 4-6.
[7] 刘春峰, 林跃进, 赵连昌. 路及其相关图的序列性[J]. 数学理论与应用, 2006, 26(4): 17-20.
[8] 刘春峰, 朱振广. 图P×C和(,)的序列性[J]. 数学的实践与认识, 2007, 10(37): 162-165.
[9] 刘春峰. 链路P()的优美性和序列性[J]. 理论数学, 2018, 8(2): 723-729.
[10] 马克杰. 优美图[M]. 北京: 北京大学出版社, 1991.
A Class of Graceful and Sequential Graph Labeling
XU Mei-jin1, LIU Chun-feng2, GAO Yang3
(1. College of Science, Liaoning University of Technology, Jinzhou 121001, China;2. Jinzhou Municipal Committee of the Political Consultative Conference, Jinzhou 121001, China;3. Basic Teaching and Research Department, Shenyang Urban Construction University, Shenyang, 110167, China)
In this paper, the graph labeling is studied. A new class of graphP(s)()is constructed by graph operations and association relations. The corresponding graceful labeling and sequential labeling are determined by the functional correspondence relation and considered different scenario, which proved that this class of graphP(s)()is indeed a graceful and sequential graph.
graceful graph; sequential graph; vertex labeling
O157.5
A
1674-3261(2021)04-0269-05
10.15916/j.issn1674-3261.2021.04.013
2020-03-13
辽宁省联合基金项目(SY2016012)
徐美进(1965-),女,山东文登人,教授,硕士。
责任编校:陈 明

