带有浮动变位轴承的高速主轴系统轴承生热研究

阳雪兵，章滔，何录忠，卜忠颉，聂威

(1.湘电风能有限公司，湖南 湘潭 411101；2.海上风力发电技术与检测国家重点实验室，湖南 湘潭 411101；3.湘潭电机股份有限公司，湖南 湘潭 411101)

主轴系统是高档数控机床的核心功能部件，主轴长时间高速运转会导致轴承发热升温，引起主轴系统零部件的热膨胀，由于结构限制，热膨胀将产生热应力，从而改变各部件的受载状态，加速轴承的摩擦磨损，降低主轴系统的加工精度，缩短主轴系统服役寿命。随着高速主轴技术的发展，浮动变位轴承广泛用作高速主轴系统的支承轴承，浮动变位轴承的内圈无沟道，内圈相对外圈可以实现轴向自由移动，因此，可以释放由于主轴系统升温膨胀或者降温收缩而产生的热应力。但浮动变位轴承安装复杂，对径向卡滞非常敏感[1]，径向游隙是影响浮动变位轴承工作的重要因素，因此，开展浮动变位轴承径向游隙以及径向游隙与其他工况参数共同作用对主轴-轴承系统热特征的影响具有重要意义。

轴承发热受多方面因素的影响，主要与轴承中的摩擦力和润滑油黏度有关，诸多学者对轴承和主轴系统中轴承的发热开展了广泛的研究。文献[2]通过大量试验拟合出计算轴承摩擦力矩的经验公式。文献[3]计算了滚动轴承接触引起的摩擦热功率,润滑油黏度引起的摩擦热,保持架与套圈之间的摩擦热以及滚子端部与内圈侧的摩擦热，以解释轴承的热功率损失。文献[4-6]基于轴承拟静力学模型对高速滚动轴承各热源进行了生热计算，分析了不同工况对轴承生热的影响。文献[7]建立了一个高速主轴热-力模型，分析了热性能对主轴系统动态特性的影响。文献[8]采用有限元法分析了变预载主轴系统的温度分布，根据轴承温升的约束条件预测主轴系统中轴承可变预紧力。文献[9]建立了机械主轴热力学有限元模型，得到系统的稳态热、温升变化以及温度场分布。文献[10]采用数值方法估算了主轴系统中角接触球轴承的摩擦力矩，并用有限元法对主轴-轴承系统进行了热分析。文献[11]建立了主轴系统热-变形耦合的瞬态热网络模型，实现了主轴-轴承系统温度场与变形的耦合分析，预测了系统中关键零部件的温升情况。文献[12]建立了高速主轴前轴承及其周围环境的综合热网格模型，对轴承温度进行了预测。文献[13]综合考虑外载荷的影响，利用主轴-轴承径向热力耦合热网络模型分析了轴承运转的发热特性。文献[14]建立了高速主轴前轴承的优化综合热网格模型，用广义欧姆定律预测了高速角接触球轴承的温升。文献[15]提出了一种高速主轴系统热特性闭环迭代建模方法，分析了高速主轴系统的热-结构相互作用特性。文献[16]基于主轴-轴承准静态模型，计算了轴承摩擦热功率，研究结果表明轴承外圈倾角越大，轴承发热功率越大。文献[17]基于角接触球轴承的准静态五自由度模型，对主轴-轴承系统的发热功率进行了准静态分析，结果表明合理的非均匀预紧力可降低轴承的发热功率。

综上所述，目前的主轴-轴承系统热分析中，支承轴承主要以角接触球轴承为主，而对于带有浮动变位轴承的主轴-轴承系统发热问题的研究还未见报道，认识也比较有限，各种因素对其发热的影响需要深入探讨。因此，首先简单介绍角接触球轴承和浮动变位轴承共同支承的主轴-轴承系统模型；然后推导轴承摩擦热功率计算模型，计算不同浮动变位轴承径向游隙、主轴转速和系统预紧力条件下主轴系统中各轴承的摩擦热功率；最后讨论各种工况参数对主轴系统中轴承摩擦生热的影响。

1 主轴-轴承系统

1.1 结构

主轴-轴承系统结构如图1所示，图中Oxyz为系统惯性坐标系，Okxkykzk为第k套轴承的局部坐标系。主轴由2套角接触球轴承和1套浮动变位轴承支承，主轴运转时浮动变位轴承的内圈相对外圈能够轴向自由浮动。主轴-轴承系统使用刚性预紧弹簧对角接触球轴承施加轴向预紧力，实现主轴系统的预紧。

图1 主轴-轴承系统结构示意图

1.2 模型

主轴系统模型包含轴承模型和主轴模型，目前已有众多学者提出了主轴-轴承系统的建模方法，各有侧重，基于研究的问题，本文采用文献[18]提出的主轴系统模型分析系统的受载与变形。该系统模型由球轴承的拟静力学模型与主轴模型组成，球轴承拟静力学模型摒弃了沟道控制理论，考虑了球的离心力和陀螺力矩，共包含3类方程(球的速度方程、球的平衡方程以及内圈的平衡方程)；主轴模型则采用Timoshenko梁单元建立轴的有限元平衡方程。文献[18]的模型中主要研究对象为角接触球轴承，本文主轴系统中存在浮动变位轴承，其球与内外沟道的挤压关系与角接触球轴承的关系略有不同，以下详细说明。

外圈固定、内圈旋转的角接触球轴承运转前后，球心和内外圈沟曲率中心的相对位置如图2所示。当轴承静止且仅承受静态载荷作用时，球心O与内、外圈沟曲率中心Oi，Oe三者共线，当轴承运转后，由于球离心力的影响，球心和内圈沟曲率中心位置均发生了移动，三者不再共线。图2中球心与内、外圈沟曲率中心的几何关系式为

(1)

式中：D1j，D2j分别为内、外圈沟曲率中心的轴向和径向距离；fi，fe分别为内、外圈沟曲率半径系数；D为外径；α0为球的初始接触角；ri为内圈半径，ri=0.5Dpw+(fi-0.5)Dwcosα0，其中Dw为球直径，Dpw为球组节圆直径；φj为第j个球的方位角；δx，δy，δz，θx，θy为内圈中心Ok的位移；δa为轴向预载荷引起的外圈位移；Gr为轴承径向游隙。在文献[18]的模型中，球中心相对外圈沟曲率中心的水平与竖直距离(X1j，X2j)和摩擦因数μ设为待求的未知量，根据D1j，D2j以及图2中的几何关系，可以表示球与内外沟道的挤压变形。

图2 角接触球轴承球心和沟曲率中心的相对位置

由于浮动变位轴承的内圈相对外圈可以自由轴向移动，因此，只有内圈相对外圈的径向位移才能导致球的挤压变形，如图3所示。浮动变位轴承的接触角为0，在第j个球位置处，其内沟道相对外沟道的径向移动距离可表示为

图3 浮动变位轴承球心和外圈沟曲率中心的相对位置

(2)

仍然以球与外圈沟曲率中心的径向距离为未知量，根据图3中的几何关系可表示球与内外沟道的挤压变形。与角接触球轴承相比，浮动变位轴承的拟静力学模型仅包括球的径向平衡方程与轴承径向平面内的平衡方程。

1.3 参数

轴承布置的位置参数与轴的尺寸参数如图4所示。角接触球轴承、浮动变位轴承及主轴的基本结构参数分别见表1—表3。1#角接触球轴承为预紧轴承，主轴系统的联合载荷作用在距离主轴左端162 mm处的A点，载荷分别为Fx=2 000 N，Fy=3 000 N和Fz=-1 000 N。润滑剂黏度为7.8 mm2/s。轴承和轴的弹性模量为206 GPa,泊松比为0.3，密度为7 890 kg/m3。

图4 主轴-轴承系统有限元结构简图

表1 角接触球轴承的基本结构参数

表2 浮动变位轴承的基本结构参数

表3 主轴基本结构参数

2 轴承摩擦生热模型

影响轴承摩擦生热的因素有很多，大量的研究表明，球与沟道接触界面滑动产生的摩擦热和由于润滑剂黏度导致的摩擦热是轴承生热的主要原因。

2.1 滑动速度

为计算球与沟道接触面上由于相对滑动导致的摩擦热，必须先确定球与沟道表面的相对滑动速度。

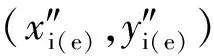
图5 角接触球轴承球与沟道运动学关系

,(3)

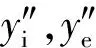
(4)

式中：Ri,Re分别为内、外沟道半径。

此外，球相对沟道自旋产生的滑动速度为

(5)

如图6所示，基于(3)式和(5)式可以计算得到球与沟道椭圆接触区上任意点处的相对滑动速度矢量为

图6 接触区域的相对滑动速度

(6)

式中：i″,j″分别为x″和y″方向的单位向量。

对于浮动变位轴承，球的自转轴线与主轴轴线平行，因此令(3)式—(6)式中的节圆角β=0°，即可计算得到浮动变位轴承球与沟道的相对滑动速度。

2.2 球与沟道滑动摩擦热功率

球与内外沟道椭圆接触区域由于相对滑动产生的摩擦热功率Hi(e)为

(7)

式中：J为转换系数(从N·mm/s转换为W)；τi，τe分别为球与内、外沟道椭圆接触区上任一点的摩擦切应力，MPa；Δvi，Δve分别为球与内、外沟道椭圆接触区任一点的相对滑动速度，mm/s；Ai，Ae分别为球与内、外沟道的椭圆接触面积，mm2。

(8)

式中：Qi(e)为球与内外沟道之间的接触载荷，N；bi(e)为球与内外沟道椭圆接触区短半轴，mm。

对所有球与沟道接触区域的局部摩擦热功率求和，可计算出整个轴承的滑动摩擦热功率为

(9)

2.3 润滑剂黏滞阻力产生的摩擦热功率

处于正常润滑状态运行的轴承，文献[2]推导出由于润滑剂黏滞阻力引起的黏滞摩擦力矩Mν的经验公式为

(10)

式中：f0为取决于轴承类型和润滑方法的系数，角接触球轴承通常f0=2；ν0为润滑油运动黏度，mm2/s；n为主轴转速，r/min。

轴承润滑剂黏滞阻力产生的热功率Hν可通过下式计算

(11)

因此，轴承总摩擦热功率为

H=Hhd+Hν。

3 主轴系统轴承摩擦热功率结果分析与讨论

3.1 浮动变位轴承径向游隙对系统中轴承生热的影响

主轴转速为10 000 r/min，1#角接触球轴承预紧力为1 000 N，浮动变位轴承径向游隙对主轴系统中轴承摩擦热功率的影响如图7和图8所示，图8中1#球与x轴夹角为0°。需要说明的是，由于浮动变位轴承中球自转轴线与主轴轴线平行，无陀螺效应，因此，无需求解球的力矩平衡方程以及球的摩擦因数，为计算浮动变位轴承的滑动摩擦热功率，摩擦因数参考角接触球轴承的结果选取，目前的研究中角接触球轴承各球摩擦因数的计算值基本为0.010～0.064，故浮动变位轴承摩擦因数取0.050。由图7可知，浮动变位轴承滑动摩擦热功率和总摩擦热功率远小于两角接触球轴承的摩擦热功率。这主要是由于浮动变位轴承直径较小，球与沟道接触区域的滑动速度较小且润滑剂的黏滞摩擦力矩较小，因此，滑动摩擦热功率、黏滞摩擦热功率以及总摩擦热功率均较小。

图7 浮动变位轴承径向游隙对轴承滑动摩擦热功率与总摩擦热功率的影响

由图7a可知，随着浮动变位轴承径向游隙从12 μm增至36 μm，1#，2#角接触球轴承以及浮动变位轴承的滑动摩擦热功率分别降低0.1%，10.2%和28.1%，这一现象可通过图8来解释。由图8可知，浮动变位轴承径向游隙的增大，导致1#角接触球轴承中将近一半数量球的滑动摩擦热功率增大，而另一半球滑动摩擦热功率降低，且增加与降低的总幅度较为接近，因此，1#角接触球轴承滑动摩擦热功率受浮动变位轴承径向游隙影响较小；而2#角接触球轴承大部分球位置处的滑动摩擦热功率随着浮动变位轴承径向游隙的增大而显著降低，仅有少数球位置处的滑动摩擦热功率表现出升高的趋势，因此总体上，2#角接触球轴承的滑动摩擦热功率随着浮动变位轴承径向游隙的增加而降低；浮动变位轴承大部分球位置处的滑动摩擦热功率受其自身的径向游隙影响较小(这部分球接触力极小)，而少部分球位置处的滑动摩擦热功率随着径向游隙的增大而降低，因此，浮动变位轴承的滑动摩擦热功率随着径向游隙的增加而降低。

图8 不同浮动变位轴承径向游隙下轴承球与沟道接触区域滑动摩擦热功率分布

轴承滑动摩擦热功率占轴承总摩擦热功率的比值如图9所示，3套轴承的滑动摩擦热功率占总摩擦热功率的比值均不足8%，说明由润滑剂黏滞阻力产生的摩擦热功率是轴承总摩擦热功率的主要来源。尽管轴承的滑动摩擦热功率对轴承总摩擦热功率贡献较小，但能对外圈温升产生显著的影响。外沟道的滑动摩擦热功率随球位置的不同差异显著(图10)，对于长时间运转的主轴轴承，这必将导致外圈温度分布的较大差异，引起外圈的不均匀热膨胀，造成球受载差距较大，缩短轴承服役寿命。

图9 不同浮动变位轴承径向游隙下轴承滑动摩擦热功率占总摩擦热功率的比值

图10 球与外沟道接触区域滑动摩擦热功率分布

3.2 转速对系统中轴承生热的影响

浮动变位轴承径向游隙为12 μm、1#角接触球轴承预紧力为1 000 N时，不同转速下主轴系统中各轴承的摩擦生热如图11所示，3套轴承的滑动摩擦热功率、总摩擦热功率以及滑动摩擦热功率占比均随主轴转速的升高而增加，但总体而言，两角接触球轴承的摩擦热功率随主轴转速增加变化显著，浮动变位轴承的摩擦热功率变化幅度相对较小。

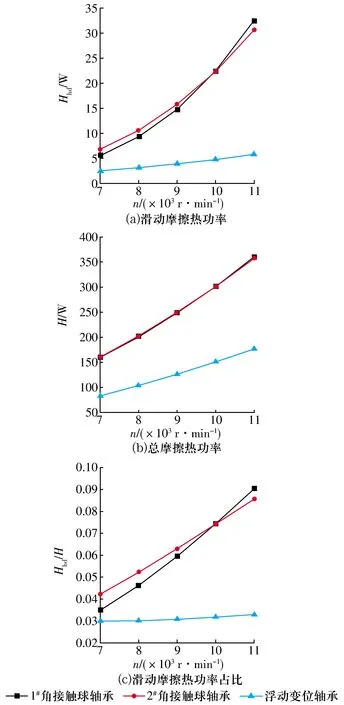
图11 不同转速下轴承的摩擦热功率

3.3 预紧力对系统中轴承生热的影响

主轴转速为10 000 r/min，浮动变位轴承径向游隙为12 μm，1#角接触球轴承预紧力从500 N增加到2 500 N时，主轴系统中各轴承的摩擦热功率如图12所示。由图12a可知:随着预紧力的增大，角接触球轴承的滑动摩擦热功率增大，预紧力从500 N增大到2 500 N，1#和2#角接触球轴承的滑动摩擦热功率分别增大了14.6%和54.1%,而浮动变位轴承滑动摩擦热功率却降低了70.0%。这是由于随着预紧力的增加，两角接触球轴承球受载增大，轴承刚度提高，主轴系统刚度也随之提高，浮动变位轴承内圈的位移减小，导致浮动变位轴承承载区球接触载荷降低。然而，由于滑动摩擦热功率占轴承总摩擦热功率比例较小，滑动摩擦热功率的增大没有导致轴承总摩擦热功率的明显变化(图12b)。另外，对于1#角接触球轴承，滑动摩擦热功率随着施加在其上的预紧力的变化在1 000 N处出现了拐点，这主要是因为预紧力的变化使1#角接触球轴承内球的接触力与速度重新分布造成的。

图12 不同预紧力下轴承摩擦热功率

3.4 浮动变位轴承外圈沟曲率半径系数对系统中轴承生热的影响

主轴转速为10 000 r/min、浮动变位轴承径向游隙为12 μm，1#角接触球轴承预紧力为1 000 N时,浮动变位轴承外圈沟曲率半径系数的变化对系统中各轴承滑动摩擦热功率的影响如图13所示，由图可知，随着浮动变位轴承外圈沟曲率半径系数从0.52增到0.56，角接触球轴承的滑动摩擦热功率基本保持不变，但浮动变位轴承的滑动摩擦热功率降低53%左右，外圈沟曲率半径系数对浮动变位轴承自身的滑动摩擦热功率影响显著。这是因为外圈沟曲率半径系数的变化显著改变了浮动变位轴承球与沟道间的滑动速度(图14)，但对接触载荷的影响较小(图15)，因此，对其他轴承的受载影响较小，这导致浮动变位轴承滑动摩擦热功率的显著变化，而角接触球轴承的摩擦热功率基本保持不变。

图13 浮动变位轴承外圈沟曲率半径系数对各轴承滑动摩擦热功率的影响

图14 浮动变位轴承外圈沟曲率半径系数不同时球与外沟道接触区域平均滑动速度

图15 浮动变位轴承外圈沟曲率半径系数不同时球与外沟道接触载荷分布

4 结论

基于主轴系统模型与轴承生热模型，分析了浮动变位轴承径向游隙、外圈沟曲率半径系数以及主轴转速、角接触球轴承预紧力对主轴系统中各轴承摩擦热功率的影响，结果表明：

1)浮动变位轴承的径向游隙影响主轴系统中各轴承滑动摩擦热功率，随径向游隙的增加，浮动变位轴承摩擦热功率降低程度最为显著；径向游隙增加也显著降低了距离浮动变位轴承较近的角接触球轴承的滑动摩擦热功率。

2)主轴转速的提高导致轴承摩擦热功率增大,角接触球轴承预紧力对轴承滑动摩擦热功率影响显著，对总摩擦热功率的影响较为微弱。

3)浮动变位轴承外圈沟曲率半径系数显著影响其自身滑动摩擦热功率，但对角接触球轴承的摩擦热功率影响甚微。

4)由润滑剂黏滞阻力产生的摩擦热功率是轴承总摩擦热功率的主要来源，而球与沟道间的滑动摩擦热功率对轴承总摩擦热功率贡献较小。