黏土广义塑性模型在FLAC3D中的数值实现与应用
林志远,熊传祥,谢永宁,黄盛锋
(1.福州大学 环境与资源学院, 福建 福州 350116;2.自然丘陵山地地质灾害防治重点实验室, 福建 福州 350116;3.福建省地质灾害重点实验室, 福建 福州 350116)
广义塑性模型由Pastor等[1]1990年系统提出,包含黏土和砂土两部分,该模型因具有简洁形式、模块化特性以及易于数值实现的特点受到学者的青睐,但前人对广义塑性模型的研究主要围绕砂土模型展开[2-4],对黏土部分的研究目前仍较为欠缺(包括理论和模型应用)[5]。国内关于黏土广义塑性模型的研究仍存在一些亟待解决的问题,如:张卫东等[6]在ADINA软件中实现了二次开发,但该研究仅针对适用于正常固结黏土的理论部分开展数值试验验证,并未涉及在超固结状态下的可行性论证,对理论模型与二次开发研究尚不完整;费康等[7]在黏土广义塑性模型框架中考虑温度影响,使得改进后的模型能够反映黏土在温度循环作用下的变形行为,但仍欠缺对改进的模型在力学加载条件下的验证。故完善黏土广义塑性模型在各种不同应力历史、不同应力路径中理论与应用研究为本研究的目的之一。
目前,已有不少学者借助FLAC3D提供的二次开发平台(UDM)开展二次开发研究,并获得显著的成果[8-15]。FLAC3D采用的显式有限差分算法能准确模拟材料的塑性流动与破坏,在求解三维岩土问题、动力问题以及高度非线性问题上有突出的优势,尤其适合作为黏土广义塑性模型数值实现的载体,以应用于实际工程分析。最重要的是,目前还未有基于FLAC3D软件的黏土广义塑性模型二次开发研究,其意味着对黏土广义塑性模型的工程应用价值的认识尚存不足,对比砂土广义塑性模型(常用于大坝变形分析[16-18])其应用价值可能被低估,具有深入探究的意义。
鉴于黏土广义塑性模型研究尚存在不足(包括可参考研究成果较少,缺乏超固结土部分理论与应用的研究,工程应用价值认识不足),以及黏土广义塑性模型的FLAC3D二次开发研究还未被开展等问题,本文开展了关于黏土广义塑性模型的FLAC3D二次开发研究。
1 黏土广义塑性模型及其差分形式
1.1 黏土广义塑性模型
黏土广义塑性模型适用于求解各种不同应力历史(正常固结与超固结)黏性土的力学特性,且得益于该模型无需明确给出屈服面和塑性势能面函数形式的特点,极大程度降低了数值实现的难度。
黏土广义塑性模型的增量形式为:
dσ=De∶dε-dλDengL/U
(1)
式中:dσ,dε分别为应力、应变增量向量;ngL/U为单位塑性流动方向向量,“L/U”分别表示加载和卸载;De为弹性刚度矩阵。
De=K·(m⊗m)+2G·[I-1/3(m⊗m)]
(2)
向量m=(1,1,1,0,0,0)T,I为单位矩阵;⊗为克罗内克积(Kronecker product),如对于向量u和v,(u⊗v)ij=uivi。K、G分别为弹性体积和剪切模量,其与平均有效应力p′的关系为:
(3)

dλ为塑性乘子(plastic multiplier),为一标量,其方程形式为:
(4)
式中:n为单位加-卸载方向向量;HL为塑性模量。假设采用相适应的流动准则,则有n=ngL/U,在三维应力空间中表达式为[19]:
(5)
式中:p′为平均有效应力,q为剪应力,θ为Lode角。其中p′,q与应力张量之间的关系分别为:
(6)
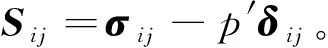
(7)
假设应力状态与Lode角无关,将公式(7)代入式子(5)中,可得三维应力空间中的塑性流动方向和加-卸载方向向量的表达式,如下式所示:
(8)
上式中,d为剪胀性关系:
d=(1+α)(Mc-η)
(9)
式中:α为材料参数;Mc为临界状态应力比;η为应力比(=q/p′ )。
式(4)中塑性模量HL是一个标量,其表达式为:
(10)
式中:γ为模型参数;ζ、ζmax分别为记录应力历史的函数与其最大值。公式(10)中其余相关函数的表达式如下所示:
g(ξ)=βexp(-β1ξ)
β=β0(1-ζ/ζmax)
(11)

1.2 本构模型的差分形式
由于FLAC3D采用的是显式三维差分算法,为了更好地实现程序化,有必要推导黏土广义塑性模型的差分形式。由式(1)可知总应变增量与应力增量的差分形式为:
Δσ=De∶Δε-ΔλDe∶ngL/U
(12)
分别用上标“N”与“O”表示更新后的应力状态和更新前的应力状态,则更新后的应力可表示为:
σN=σO+De∶Δε-ΔλDe∶ngL/U=
σI-ΔλDe∶ngL/U
(13)
σI为弹性尝试获得的应力张量。
由式(13)可知,计算更新应力σN还需解决塑性校正的问题。塑性校正主要涉及塑性流动方向向量和塑性乘子的计算。由公式(8)可知,用于塑性校正的塑性流动方向向量表达式应为:
(14)
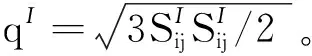
其次,塑性乘子的计算。由公式(4)可知塑性乘子的表达式,结合式(14)给出的加卸载方向与塑性流动方向向量表达式可得用于塑性校正的塑性乘子为:
(15)
此时,式(13)转变成如下式所示:
(16)
2 二次开发流程及其关键点
采用Visual Studio 2019集成开发环境(IDE)对FLAC3D软件提供的二次开发模板中的源代码(.cpp)和头文件(.h)进行修改和编写,成功将黏土广义塑性模型嵌入到软件中。编译成功的黏土广义塑性模型会生成一个动态链接库(.DLL文件)供主程序通过命令流调用。调用用户自定义模型时,FLAC3D需要历经两个步骤,首先需要通过zone config plugin命令调用插件模块,然后通过命令zone cmodel load与完整的动态链接库存储路径来实现用户自定义模型的调用。二者缺一不可。
黏土广义塑性模型的二次开发流程如图1所示,出于未考虑模型在循环加-卸载场景下的应用,省略了应力加-卸载判断这一步骤,有必要在后续研究中进行完善。实现图1所示的开发流程,核心技术在于修改源文件的初始化函数initialize()和求解函数run()。其中初始化函数仅在初始化过程被调用一次,用于模型参数和部分中间变量的初始化,以及提示初始赋值过程出现的错误;求解函数的功能则是根据主程序传入的位移信息(或应变增量信息)求解新应力。

图1 程序执行流程图
3 算例验证
3.1 单元试验
单元试验(One zone test)被广泛用于验证模型二次开发的正确性[10,13]。本节通过对比单元试验结果、试验成果(Pastor等[1])和理论结果(Python编写的计算机程序的计算结果),成功证实了黏土广义塑性模型二次开发的正确性。其中,Python程序的计算结果等效于有限差分程序中积分点上的计算结果,因此,Python程序的计算结果与单元试验的模拟结果应基本没有差别(约10-5量级)。
单元数值试验针对Bangkok黏土和Weald黏土开展了固结排水与不排水三轴应力路径验证工作。两种土样的模型参数均取自文献[1],如表1所示。其中Bangkok黏土的前期固结压力为414 kPa,超固结比为24的Weald黏土的前期固结压力为120 psi(约827 kPa)。排水与不排水三轴数值试验的brick单元的边界条件示意图如图2所示,顶部采用速度边界条件(10-6/时步)模拟室内试验应变控制加载的情形,不排水三轴试验还应调用流体计算模块,用于流固耦合计算,水的体积模量取2.2 GPa。注意施加速度边界条件时其量值不应大于10-5/时步,否则将影响数值试验模拟的精度。

表1 单元试验参数取值
正常固结Bangkok黏土的不排水和排水三轴试验的数值模拟结果、试验结果以及理论结果的对比如图3—图6所示。根据对比结果可以发现FLAC3D模拟结果与理论结果完全一致,与试验结果基本吻合,仅在有效应力路径(见图4)与排水三轴试验的应力比-体积应变曲线(见图6)的模拟结果上存在细微差别。图7与图8给出了超固结Weald黏土固结排水与不排水三轴应力应变行为的模拟结果。由结果可知,该模型较好地反映了超固结Weald黏土在排水条件下的软化与剪胀特性,以及不排水条件下的硬化特性,在一定程度上补充了文献[6]和文献[7]未开展超固结土模型研究的不足。

图2 单元试验示意图

图3 Bangkok黏土不排水三轴试验q-εs曲线

图4 Bangkok黏土不排水三轴试验有效应力路径
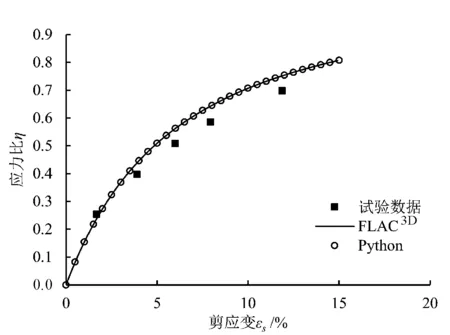
图5 Bangkok黏土排水三轴试验η-εs曲线

图6 Bangkok黏土排水三轴试验η-εv曲线
3.2 路堤堆载数值模拟
本节通过路堤堆载数值模拟进一步验证了黏土广义塑性模型的工程适用性。
该数值试验模拟了路堤填筑过程和填筑完成后的地基固结过程。考虑到路堤填筑时长(约27 h)远小于地基固结的持续时长(约3 a),且不涉及路堤填筑过程的研究,故简化分层填筑过程,采用一个逐渐增大的均布荷载等效,其最大值为50 kPa,如图9所示。由于路堤完成填筑的历时较短,该过程可近似为不排水过程。
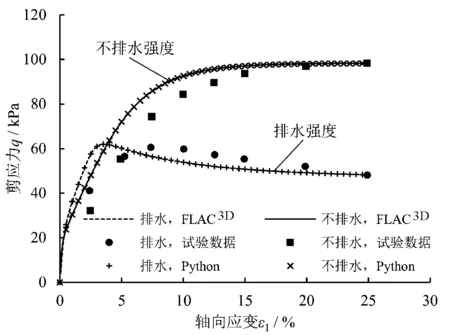
图7 超固结Weald黏土q-ε1曲线数值模拟与试验结果对比
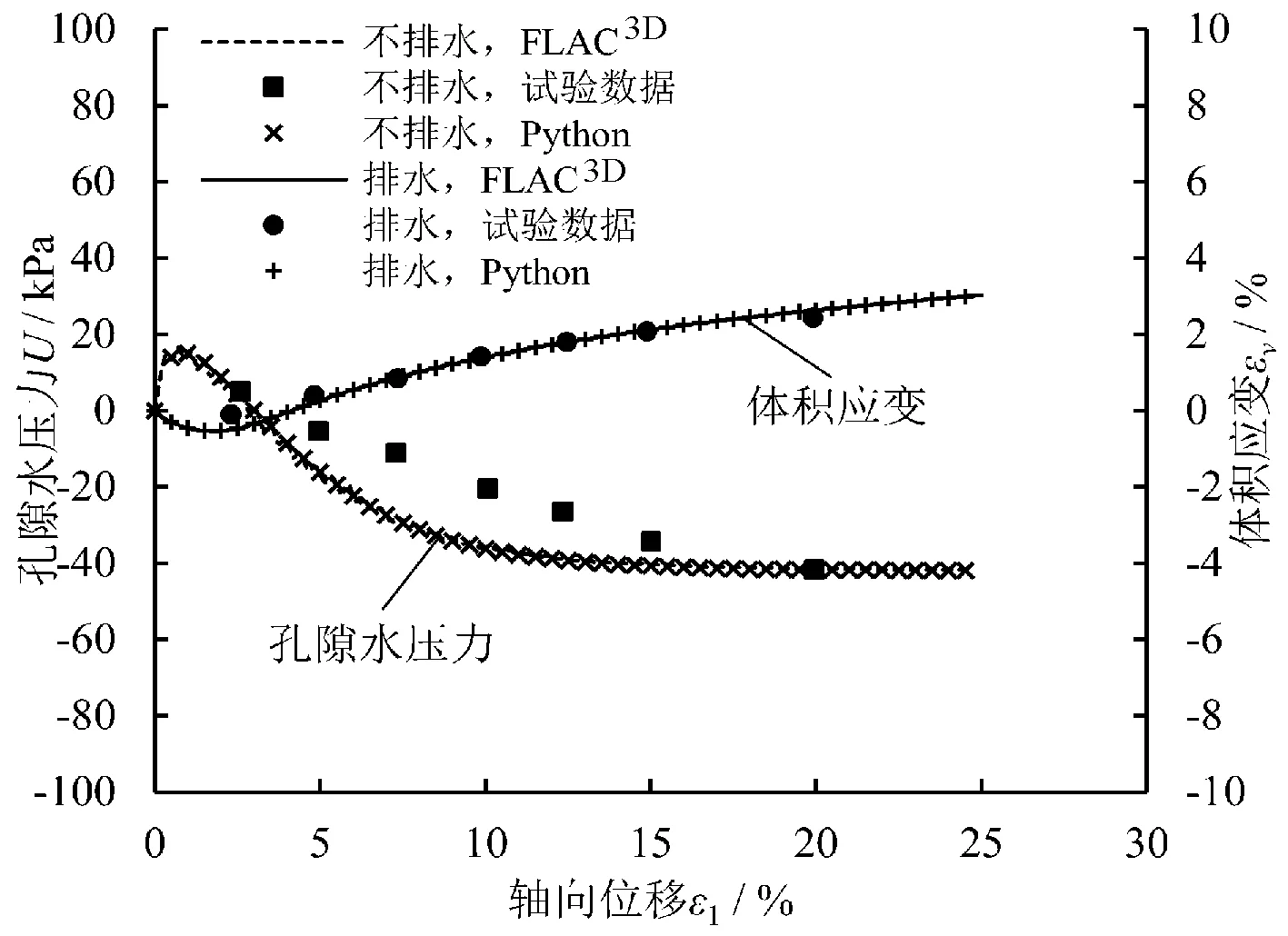
图8 超固结Weald黏土U-ε1和εv-ε1曲线数值模拟与试验结果对比

图9 路堤堆载计算模型示意图
几何模型采用30×1×20(x×y×z)的网格模拟20×1×10 m3的地基土体。地基土采用黏土广义塑性模型(clayPZ),设置地表排水。模型参数取值分别为:压缩指数(λ)0.18,回弹指数(κ)0.05,临界状态应力比(Mc)0.8,泊松比(ν)0.3,参考孔隙比(er)1.2,参数μ、β0、β1、γ、α取值分别为2、0.5、13、1.3、0.5。地基土干重度为20 kN/m3,前期固结压力为147 kPa,侧压力系数K0为0.64。模型包括两个求解过程,一是填筑不排水过程,采用局部不平衡力比值小于或等于10-4作为终止条件;二是地基固结排水过程,终止该过程的条件需满足每次迭代的不平衡力比小于5×10-5,且总求解时长达到108s(约3 a)。
孔隙水压力的演化情况如图10至图12所示。图10展示了水平距离为0.5 m处填筑开始前与结束时模型预测的孔隙水压力随深度的分布情况。由于设置地表排水,地表处的孔隙水压力仍为0 kPa,随着排水条件影响的减弱,地表附近的孔隙水压力逐渐增大,在地表以下0.5 m处达到峰值状态(62 kPa);地面以下0.5 m~1.5 m处脱离了上部荷载的直接影响范围,超孔隙水压力迅速减小;地表以下1.5 m~9.5 m的孔隙水压力受到上部附加荷载的作用孔隙水无法及时排出,产生超孔隙水压力,故其比未堆载前的孔隙水压力大。图11给出了路堤固结过程孔隙水压力在不同深度的分布情况随时间的演化。“0 d”表示未进行路堤填筑前孔隙水压力沿深度方向的分布。据分析,填筑结束时的孔隙水压力最大(见图10),而后随着时间逐渐消散,恢复至未进行填筑前的水平(见图11)。由于固结时间为一年时的水压分布已十分接近初始状态,为提高插图的可读性未展示后续两年的孔隙水压力模拟结果。图12给出了深度为1.5 m(z=8.5 m)、6.5 m、9.5 m处孔隙水压力随时间的演化情况,证实了上述分析,可以看到水压在1 a时基本消散完全。
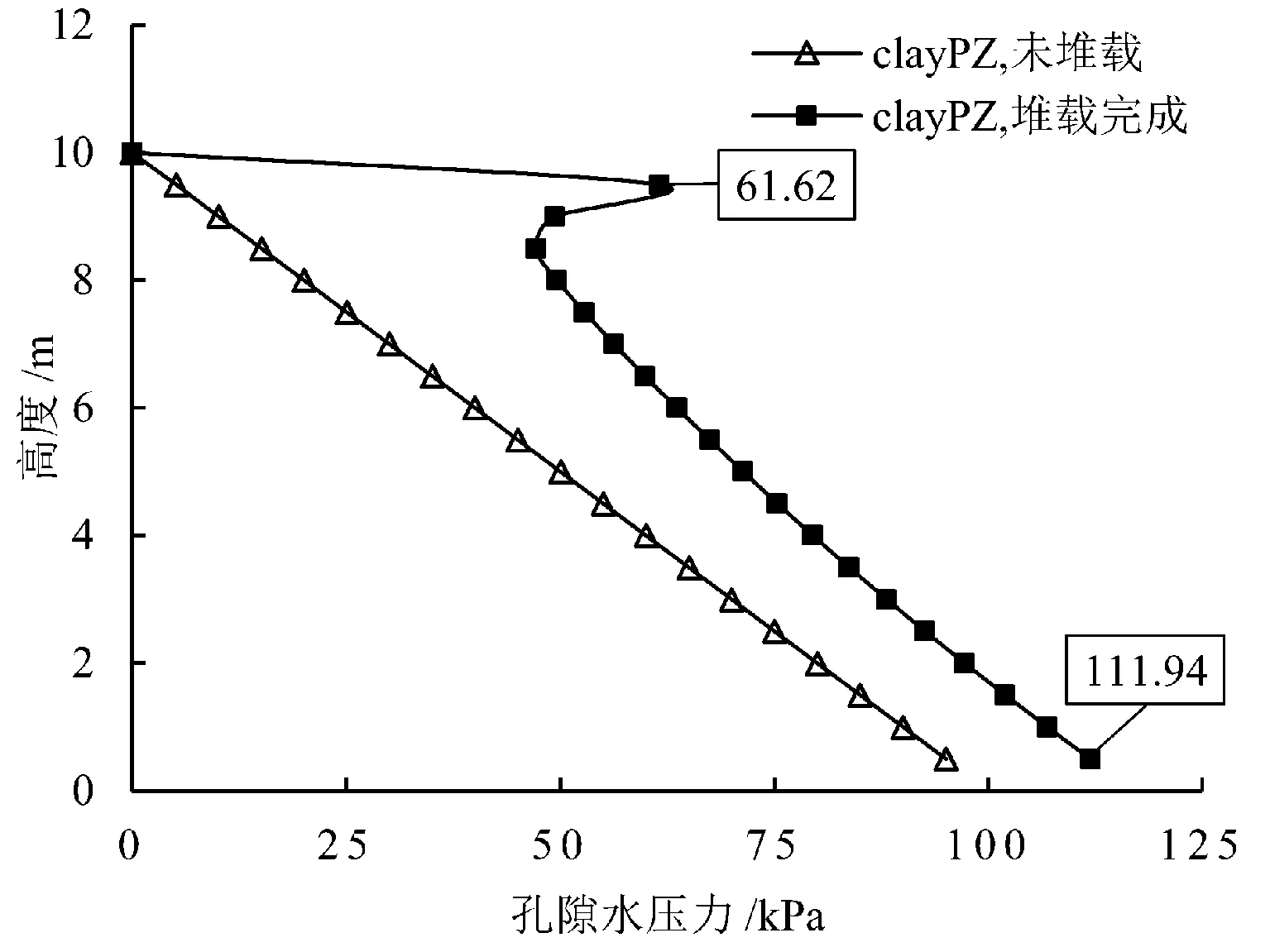
图10 堆载过程孔隙水压力的对比
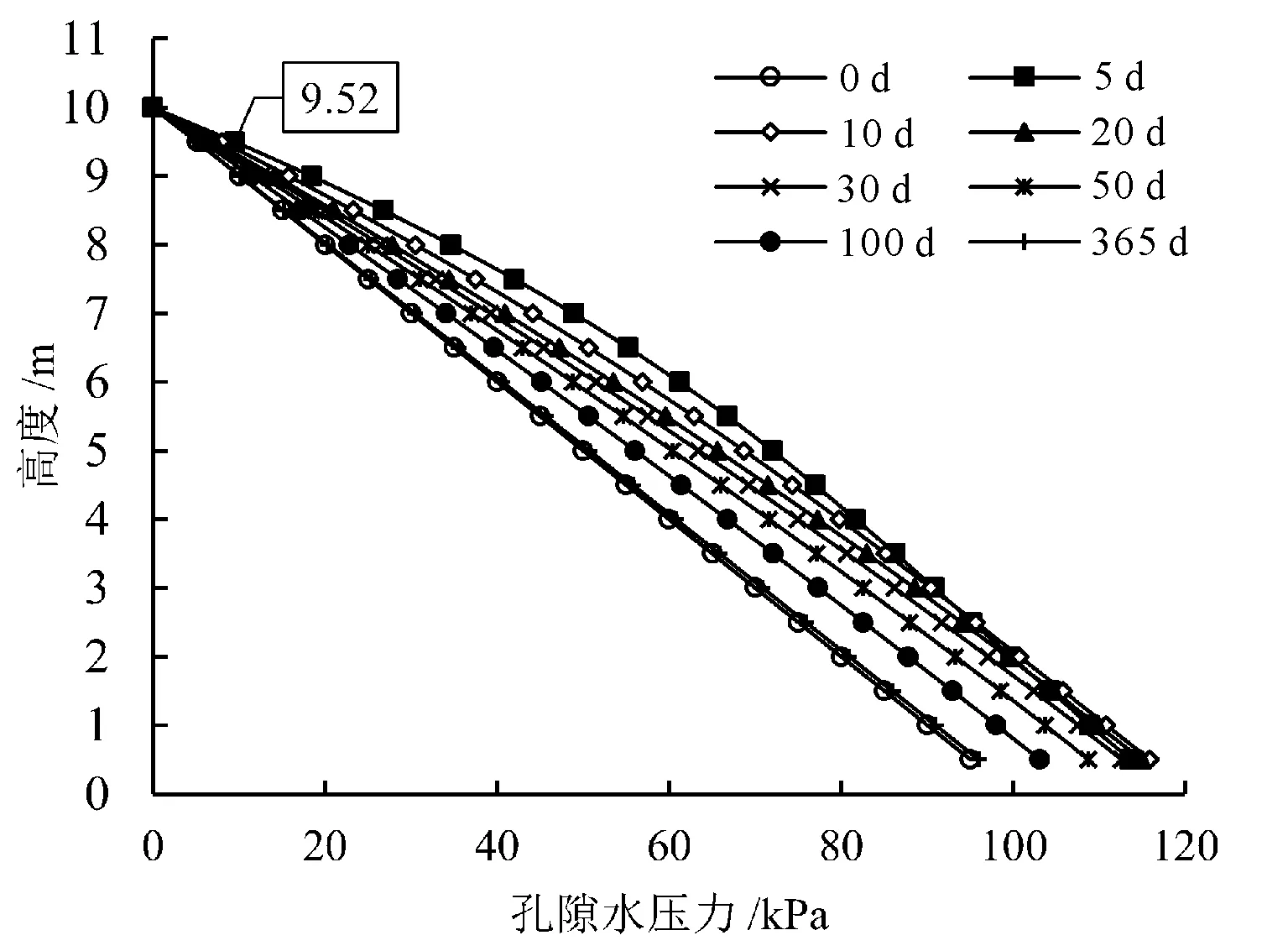
图11 固结过程不同深度孔隙水压力随时间的演化

图12 路堤堆载全过程孔隙水压力随时间的演化
路堤堆载引起的地面变形(沉降或隆起)是路堤填筑过程值得关注的问题。如图13所示,模拟结果表明堆载结束时,在填筑范围内的地面受到上部荷载作用发生沉降(最大值达0.24 m),地基土被挤出,导致周围地面发生隆起(峰值达到0.11 m)。其中堆载范围内地基土可近似为一维固结,因此其变形量可通过土体压缩模量(Es)近似计算。根据经验值可知弹性模量(E)通常为压缩模量的2~5倍,故可根据土体的初始孔隙比、回弹指数、泊松比计算获得地面附近1 m处的地基土压缩模量介于67.2 kPa~168.0 kPa,所以压缩变形范围位于0.83 m~2.07 m之间,略大于数值模拟结果。其原因为路堤填筑过程实为不排水过程,地基土并未完全固结,故其沉降量略小于估算值。而后随着时间的推移,超孔隙水压力逐渐消散,有效应力增大,土体发生固结,分析区域内(0~10 m水平距离)土体均发生下沉。符合预期分析的结果。
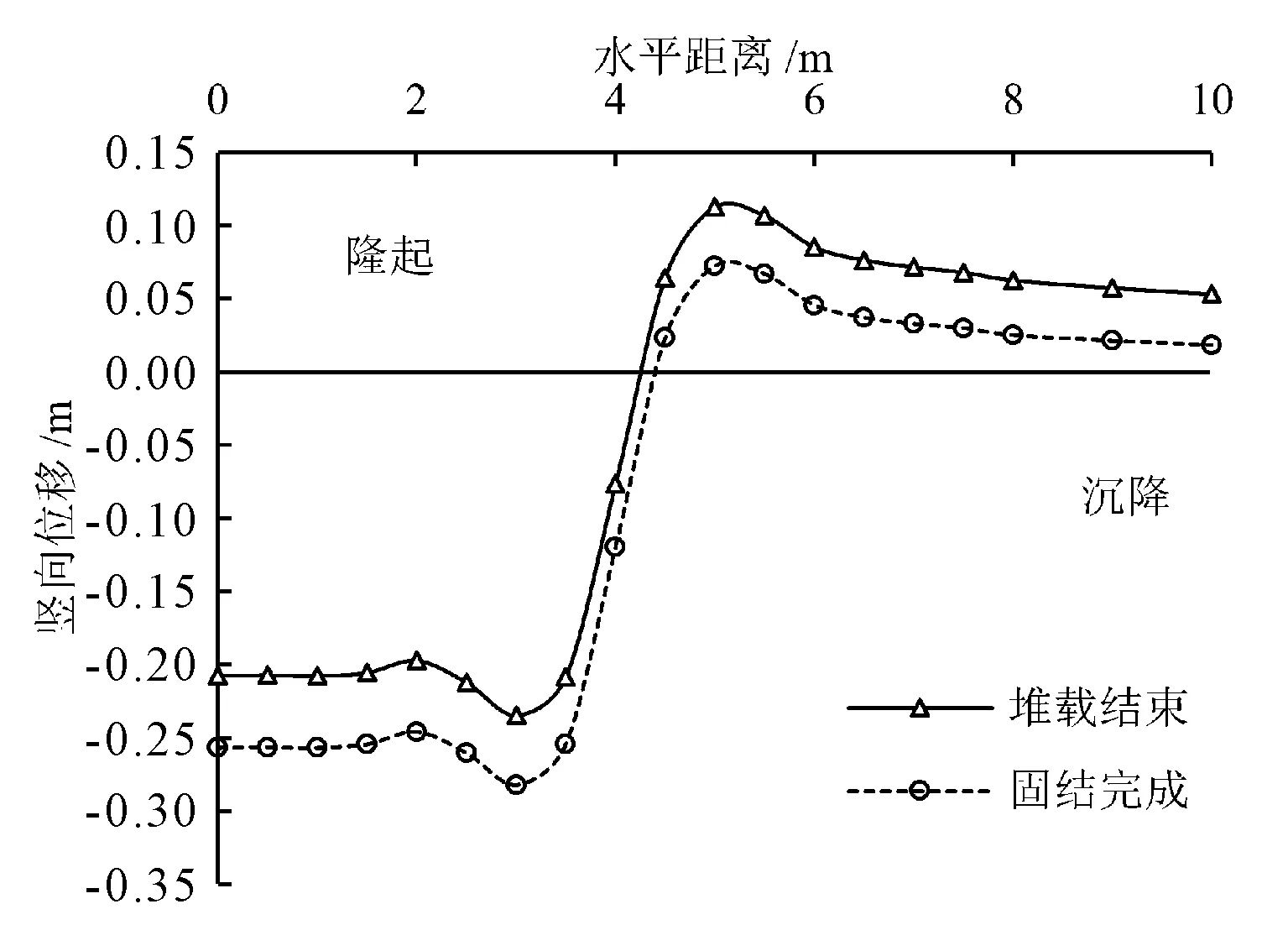
图13 堆载结束时的地面沉降分布
4 结 论
(1) 本文在FLAC3D(7.0版本)提供的二次开发平台上成功实现了黏土广义塑性模型的数值嵌入。并利用单元试验模拟了不同应力历史黏土的应力应变行为,成功证实了二次开发的可靠性与正确性。在一定程度上补充了前人在黏土广义塑性模型中关于超固结土研究的不足(文献[6-7])。
(2) 通过开展路堤堆载的数值模拟,验证了二次开发模型的工程适用性,表明了黏土广义塑性模型的应用价值,为以后研究饱和黏土相关问题时提供了新的工具。

