类比思想方法在高等数学学习中的应用

曹淑霞

【摘要】类比思想方法指依据两个不同对象有部分相同属性，从而猜想它们的其他属性也可能相同的推理方法.在高等数学教学中合理运用类比思想方法，能够帮助学生形成系统化的学习方式，更好地理解和掌握新知，继而培养学生发现问题、分析问题和解决问题的能力.

【关键词】类比思想;高等数学;应用

【基金项目】少数民族预科高等数学中类比思想方法应用的探究（ykkt201811）

事物之间是有联系的，通过与某一事物的类比会发现另外的事物某一方面的特点.因此，类比是发现问题的一种重要方法.高等数学中的概念、定理、性质较为抽象，且运算法则、计算公式繁多，不易记忆.类比思想方法的合理应用能够让学生将已有的知识转移到新知中，更好地帮助学生建立知识体系.通过类比来学习不仅可以使学生温故知新，而且可以帮助学生更好地理解、记忆和应用所学知识.

1.1 数列极限和函数极限定义的类比

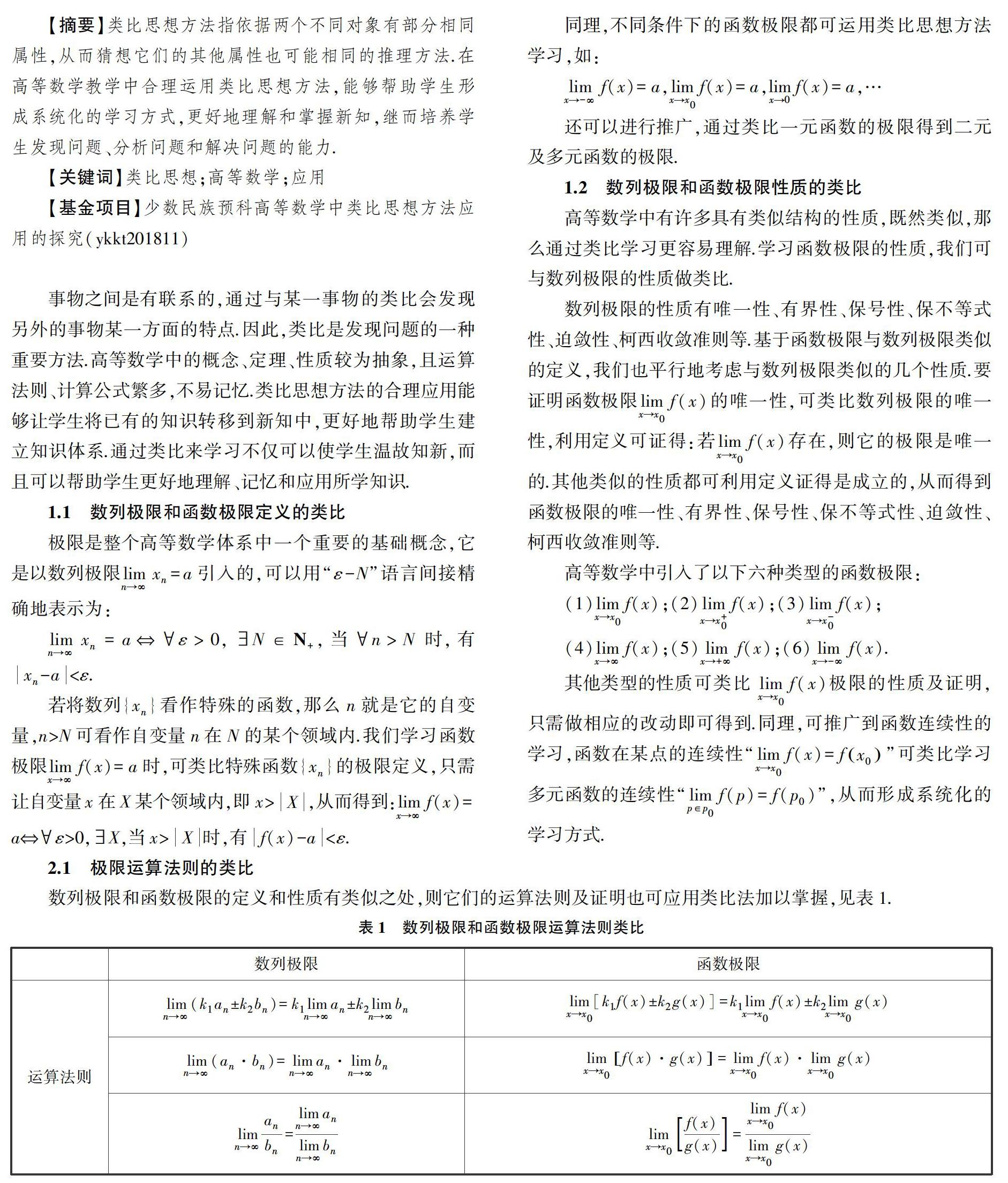
2.1 极限运算法则的类比

数列极限和函数极限的定义和性质有类似之处，则它们的运算法则及证明也可应用类比法加以掌握，见表1.

2.2 導数与微分运算法则的类比

导数和微分是有联系的.对于一元函数而言，可微必可导，可导必可微.实际上，导数运算和微分运算是平行的，也就是说每一个微分运算都对应一个导数运算，反过来也是如此.不妨把dydx看作一个分式，则可将dy=f ′（x）dx化为f ′（x）=dydx的形式，那么函数的导数就等于函数微分与自变量微分的商.这样它们的一些运算法则便具有了类似性，则可通过类比导数的运算法则学习微分的运算法则，见表2.

类比思维是对知识的一种迁移，在高等数学中有着非常重要的作用，它能起到严格的逻辑推理所不能达到的效果.教师在教学中指导学生利用类比思想方法学习，学生更容易理解新知，更快捷地形成知识体系，并能够在学习和生活中有意识地应用类比思想方法解决问题，开拓创新.

【参考文献】

[1]仲秀英.波利亚的类比思想与数学课程改革[J].重庆师范学院学报（自然科学版），2003（03）：84-86，91.

[2]王晓燕，王厚增，吕丽娇.浅析类比的思想方法在高等数学教学中的应用[J].商业经济，2017（03）：171-173.

[3]朱彩兰.类比法在高等数学教学中的应用[J].长沙铁道学院学报（社会科学版），2014（04）：127-128.

[4]张友梅.类比思想在高等数学教学中的应用[J].开封教育学院学报，2014（04）：123-125.

[5]施静，李巧仪.浅谈类比思想在高等数学中的应用[J].知识文库，2016（20）：71-72.

[6]张卿.浅谈数学思想在高等数学中的应用[J].科技资讯，2018（35）：254，256.

[7]朱鹏翚.数学思想方法在高等数学教育教学中的作用[J].韶关学院学报，2017（05）：79-82.