地铁盾构断面椭圆度检测及数据分析研究

贺 磊，蔡乾广，许诚权，冯 耀

（1.南京市测绘勘察研究院股份有限公司，南京 210005；2.南京地铁运营有限责任公司，南京 210012）

1 研究背景

近年来，随着我国各大城市地铁建设的快速发展，地铁数量和运营里程不断增加，乘坐地铁出行已成为大众主要的交通方式之一。在与日俱增的地铁隧道建设竣工验收和运维监护工作中，盾构隧道断面测量是一项重要的工作。

地铁隧道受自身建设、运营动荷载和周边环境等综合因素的影响，其结构处在长期缓慢变形的状态。当变形积累到一定程度时，管片一般会出现裂损、错位和渗漏等病害，甚至导致隧道结构失稳，引发严重的安全事故。而隧道断面椭圆度与各隧道病害指标均有很强的相关性，可作为描述隧道病害程度和隧道管片维修整治的重要指标。管片结构的力学研究表明，当管片椭圆度小于 5‰时，则隧道可以被认为处于完全健康的状态[1-5]。

目前，在盾构隧道竣工限界检核和断面收敛监测中，采用的方法多种多样，一般采用直接测量和间接测量两种。直接测量是采用吊铅锤、水平尺来设置隧道腰线两侧的测点，通过全站仪、测距仪进行测量；间接测量是使用全站仪、断面仪、三维激光扫描仪等设备进行隧道的全断面测量，并通过采集数据、粗差剔除、椭圆拟合及参数计算等步骤，获取隧道限界和椭圆度[6-8]。

下面介绍盾构管片椭圆度测量中使用的几种方法，并通过大量的实例断面数据统计和对比分析，得出盾构断面变形的相关特点。分析由于旋转角的存在而对常规水平收敛的影响，为保证监测数据的可靠，在盾构收敛监测中以管片椭圆长轴变化量作为管片净空收敛值。

2 盾构隧道椭圆度测量方法

2.1 直接测量

先找到隧道断面两侧水平腰线测点，直接测量确定隧道管片的水平直径。一般使用铅垂或水平尺，在断面腰线两侧水平方向上，找到有最长水平直径的腰线测点，并用反射片或油漆做好测点标记；使用全站仪或测距仪进行测量，直接量取断面的水平直径。在地铁监测项目中，通常采用这种方法进行盾构管片的水平收敛测量[9]。

2.2 间接测量

全站仪全断面测量：在隧道断面上设置全站仪，并在该环设置特征点，以保证监测断面精确垂直于该环管片；采用免棱镜，按照全站仪机载断面测量程序进行测量，一般项目断面测点步距为20 cm(见图1)。这种方法效率较低，目前应用较少。

图1 全站仪全断面测量示意Figure 1 Schematic of total station full section measurement

在全站仪数据采集后，进行全断面椭圆拟合处理，椭圆采用二次曲线方程表示为

一般采用基于代数距离最小二乘法来进行数据拟合处理，式(2)中v(m，ni，l)为断面测点(xi，yi)至椭圆曲线v(m，n，l)=0的代数距离。以断面上各点代数距离平方和最小值作为平差条件进行计算，求解出椭圆参数如下：

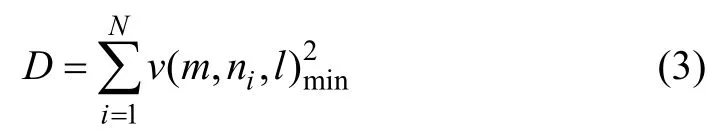
取极值对参数求导，有

再根据投影变换公式[1]计算出椭圆几何参数，如椭圆中心坐标、长半轴、短半轴和旋转角等。

三维激光扫描：一般使用移动式三维激光系统(见图2)对隧道区间进行扫描，通过里程号调取对应里程的管片点云数据；先进行粗差剔除和切片处理，然后进行全断面椭圆拟合以及参数提取，拟合方法参考全站仪全断面拟合。

图2 徕卡SiTrack：One移动扫描系统Figure 2 Leica sitrack: mobile scanning system

目前这种方法应用得越来越多，是近几年地铁隧道测量的主要方向之一；其优点是快速、方便且信息全面，通过海量点云数据的处理进行信息挖掘，提取与地铁运营维保相关的信息。

一般为了与直接测量验证、比对，通过间接法测量，最后在拟合好的椭圆上量取过椭圆中线的水平直径，与前期以及设计参数进行比较，得到管片结构的水平收敛情况。

3 管片结构变形数据分析

笔者针对内径5.5 m、外径6.2 m盾构管片，近2000环断面测量实例数据进行统计，包括直接测量、全站仪全断面测量、移动式三维激光扫描等数据，分析了管片椭圆的旋转角、横向收敛、椭圆度等参数间相互关联和分布情况，统计数据如表1所示。

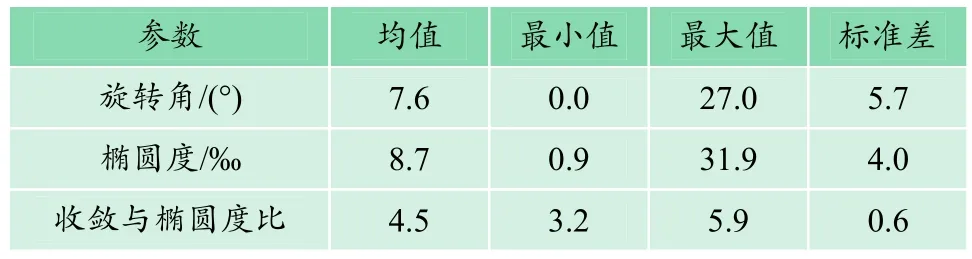
表1 管片椭圆参数统计Table 1 Segment ellipse parameter statistics

数据统计显示，旋转角在 0～27°之间，均值为7.6°(数据已取正)，如图3所示，旋转角在均值及以下范围的管片数量占比为58%，两倍均值范围内的管片数量占比为88%。经数据统计分析，并结合工程段区间线路情况，发现管片旋转角与隧道区间线性、管片收敛无明显的相关性。

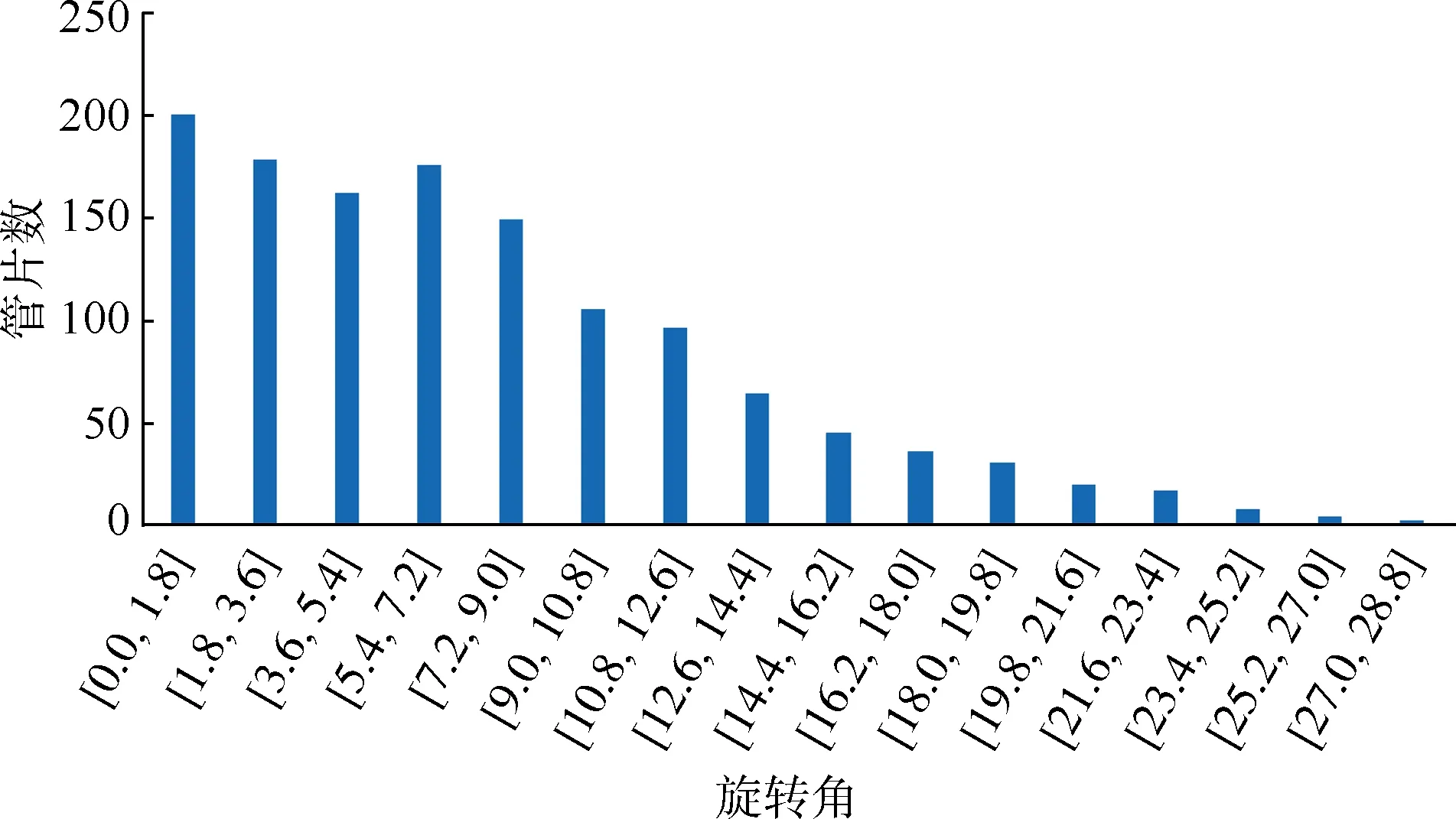
图3 管片椭圆旋转角分布Figure 3 Segment ellipse rotation angle distribution

图4为隧道对应管片横向收敛与椭圆度曲线，可见横向收敛与椭圆度有很强的相关性。

图4 管片收敛及椭圆度曲线Figure 4 Segment convergence and ovality curve

盾构断面由管片拼接而成，有自身结构变形特点。为分析盾构断面的横向收敛与纵向收敛的相关性，将对应环片横向收敛值与椭圆度相比，比值i计算如下：

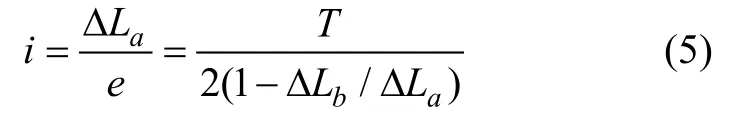
或

式中：a为管片椭圆长半轴，b为短半轴，T为管片外径，t为管片内径，椭圆度，横向收敛ΔLa=(2a-t)，纵向收敛 ΔLb=(2b-t)。

根据样本数据计算和统计，i在3.2～5.9之间，均值为4.5，其直方图接近正态分布，标准差为0.6(见图5)。i值接近4.5，即管片纵、横向收敛比值接近0.3。

图5 管片收敛与椭圆度之比Figure 5 Segment convergence to ovality ratio

4 椭圆旋转角对水平直径测量影响

在一般监测项目中，以水平收敛作为盾构管片收敛指标，而管片收敛最大值在椭圆长轴基线方向，当椭圆的长半轴在水平方向上时，水平直径才等于长轴。由于管片受自身结构、围岩应力以及长期性的列车动荷载等影响，管片变形椭圆存在一定的旋转角度。

如图6所示，管片椭圆长半轴为a，短半轴为b，旋转角为θ，T为管片外径，椭圆度，PP′即为水平直径。

图6 椭圆旋转示意Figure 6 Schematic of elliptical rotation

由平面几何关系得到

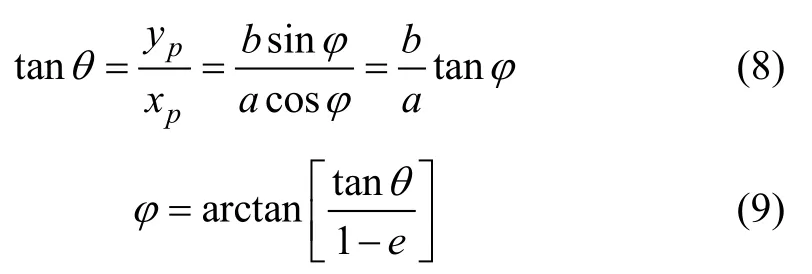
旋转角引起的管片横向直径与水平直径的偏差值Δl为

将式(7)代入式(10)，可得

管片设计内径为5.5 m，根据上面的数据统计，管片横向收敛值与椭圆度的比值取 4.5，旋转角取均值7.6°及两倍均值15.2°，分别代入式(11)进行计算。当横向收敛在2、4、6、8 cm时，椭圆长轴与水平直径的差值如表2所示，偏差值随旋转角变化曲线如图7所示。

表2 管片椭圆长轴与水平直径差值统计Table 2 Statistical table of difference between major axis of segment ellipse and horizontal diameter

图7 长轴与水平直径之差随旋转角度变化曲线Figure 7 Curve of difference between long axis and horizontal diameter with rotation angle

由上述的图表可知，旋转角按两倍平均值，当横向收敛为2 cm时，偏差值就已超过3 mm。

由此可见，在盾构隧道收敛监测中，该偏差不能忽略，应以椭圆断面的长轴作为观测值，采用断面拟合计算管片收敛。

5 结语

地铁隧道断面测量是地铁隧道竣工检测和运营期监测工作的重要内容，其断面收敛是管片维修整治的主要评估参数，对收敛测量的准确性和精度有非常高的要求。

笔者介绍了常用的几种断面椭圆度测量的方法，并用大量的工程实例数据进行统计分析，发现了管片结构断面变形参数间的相关性和规律。通过计算分析发现，在地铁隧道监测项目中，盾构横向收敛作为管片结构安全评估的重要参数，应以椭圆长轴作为收敛基线，这样更能客观反映实际变形情况。