解决约束伪凸优化问题的神经网络模型
张 坚,李国成
(北京信息科技大学 理学院,北京 100192)
0 引 言
近年来,随着科技的进步,神经网络因其大规模实时并行计算的特点被广泛用于解决工程应用和科学研究中遇到的优化问题。神经网络优化算法始于Hopfield和Tank[1-2]在1985-1986年的工作。他们将Hopfield型神经网络[3-4],用于解决旅行商(TSP)问题及非线性光滑优化问题,并取得巨大成功。
基于Hopfield和Tank开创性的工作,许多研究者针对光滑优化问题,提出了不同的神经网络优化模型。例如,Kennedy等[5]为解决非线性规划问题,提出了带惩罚参数的动态正则非线性规划电路(NPC)。Xia等[6]为解决约束优化问题,提出了投影算子神经网络模型。Hu等[7]针对一类二次规划问题提出了一个改进的对偶神经网络模型,并将它用于解决赢者通吃问题,等等。但上述模型无法解决非光滑优化问题。这时,人们尝试引进新理论、新方法。例如,微分包含理论及Clarke非光滑分析等。
Forti等[8]基于微分包含及Clarke次梯度理论,提出了一种广义神经网络模型用以解决非光滑非线性优化问题(G-NPC)。Bian等[9-10]为解决非光滑非凸优化问题,提出了基于次梯度的神经网络;同时较为系统地研究了Rn中的非光滑优化问题,并提出了基于微分包含理论并带有精确罚因子的神经网络。Li等[11]基于微分包含理论及精确罚函数的思想提出了一种单层的递归神经网络来解决不等式约束的非凸优化问题。
遗憾的是,精确罚因子计算复杂且须在网络运行前给出,同时取值不同也影响神经网络的性能。这促使研究者们倾向不带精确罚因子的神经网络。比如,Qin等[12]针对非光滑凸优化问题,提出了不带精确罚因子的双层神经网络。但它相较单层网络,计算复杂度有所增加。鉴于此,Qin等[13]针对带有等式和不等式约束的伪凸优化问题,提出了不带精确罚因子的单层神经网络。回晓丹[14]针对带凸不等式约束的伪凸优化问题提出了基于微分包含理论和罚函数思想的不带精确罚函数但含有粘性正则项的单层递归网络模型。Bian等[15]则利用光滑逼近的方法,提出了解决广义凸约束的非光滑伪凸优化问题的神经网络。但该网络的初始点必须选在等式约束的范围内,降低了适用性。此外,喻昕等[16-18]也提出了基于微分包含理论且不带精确罚因子的神经网络模型以解决约束伪凸优化问题。
为解决凸不等式约束的非光滑伪凸优化问题,本文基于微分包含理论和罚函数思想,构建了不带精确罚因子的神经网络模型。本文的网络模型与文献[18]一样巧妙地利用了凸函数的性质,从而能够在有限时间内收敛到可行域,且永驻其中。同时,借助于伪凸函数的性质,本文的网络模型最终能够快速收敛到原优化问题的最优解集。本文最大的亮点在于引入变步长,并给出了变步长选取原则及两个选取公式。变步长的引入使得网络的收敛效率有了极大的提升。
1 问题描述及预备知识
本节首先阐述所要研究的问题,然后给出一些必要的预备知识。
1.1 问题描述
本文研究如下问题:
minimizef(x)
subject togi(x)≤0i=1,2,…,m
(1)
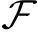
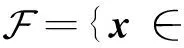
问题(1)的最优解集设为:

本文总是假定:

1.2 预备知识
定义1设X,Y均为Rn的非空子集。若∀x∈X都有非空子集F(x)⊆Y,则称F:X→Y为集值映射。若∀x0∈X,V⊇F(x0),都存在x0的一个邻域U使得F(U)⊆V,则称F在x0处上半连续(u.s.c)。若F在X的每一点处都上半连续,则称F是上半连续函数。
定义2设函数f在x点处附近Lipschitz,则f在x点处沿方向υ∈Rn的广义方向导数为:
此时,f在x点处的Clarke广义梯度定义为:
∂f(x)={ξ∈Rn∶f°(x;υ)≥〈υ,ξ〉,∀υ∈Rn}
定义3若函数f:Rn→R在x点附近Lipschitz且满足以下两个条件:
1) ∀υ∈Rn,单边方向导数
存在;
2) ∀υ∈Rn,f′(x;υ)=f°(x;υ)
则称f在x点正则。若f在其定义域的每一点都正则,则称f为正则函数。
命题1[10]设f:Rn→R在x点附近Lipschitz,
1) 若f在x点严格可微,则f在x点正则;
2) 若f是凸函数,则f在x点正则。

命题3[10](链式法则) 如果f(x)∶Rn→R在x(t)处正则,且x(t):[0,+∞)→Rn在t点可导同时在t点附近Lipschitz,那么

命题5[10]若f:Rn→R为凸函数,则有
ξ∈∂f(x)⟺∀y∈Rn
f(y)≥f(x)+〈ξ,y-x〉
定义5对连续函数f:Rn→R,若∀x,y∈Rn,有
∃η∈∂f(x)
s.t.〈η,y-x〉≥0⟹f(y)≥f(x)
则称f为伪凸函数。
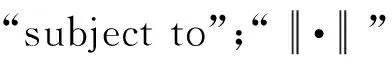
2 构造神经网络模型
本节根据惩罚函数的思想构造网络。考虑如下函数:
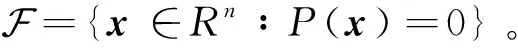
I0(x)={i∶gi(x)=0 ∀i∈I}
I+(x)={i∶gi(x)>0 ∀i∈I}
再根据命题1到命题3,得到P(x)在x点的Clarke广义梯度为:
∂P(x)=

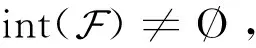

(2)

与已有模型性能比较如表1所示。

表1 不同模型的性能比较
表1表明,本文的神经网络模型同文献[13]和[15]中的模型相比是有一定优势的,至少可行域无需有界。而与文献[14]及[18]中的模型相比,因为彼此都是针对凸不等式约束伪凸优化问题的神经网络优化模型,故它们具有诸多相似的优点。比如:无需计算精确罚因子,初始点的选取任意,可行域无需有界,能够快速收敛到原优化问题的最优解集等。不同点在于,与文献[14]相比,本文的神经网络参数更少,不含时间粘性正则项,仅需目标函数的Clarke广义梯度信息就能起到与时间粘性正则项相似的作用,即加速网络收敛。而与文献[18]相比,在某种程度上,本文可看作其改进模型,针对性更强,在满足精度要求的条件下收敛速度也更快。
3 主要结论
本节证明网络(2)的优化性能。
定理1对任意初始点,网络(2)都存在至少一个局部解。
证明易知网络(2)的右端是一个非空紧凸的上半连续集值映射。根据命题4,对任意初始点x(t0)=x0∈Rn,网络(2)都存在至少一个局部解x(t)(t∈[0,T))。其中T表示局部解的最大存在时刻。证毕。
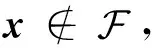

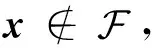
其中,I+(x)非空。又∂P(x)是非空紧凸的上半连续集值映射,则∀η∈∂P(x),存在αi∈[0,1]使得
根据命题5,
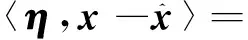
证毕。
注解1文献[18]虽给出了引理1但并未给予证明,这里给出完整的证明过程以及更清晰合理的表述。

成立。

引用引理1,有
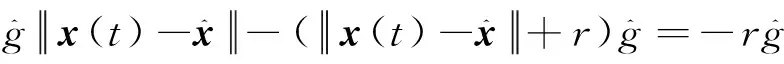
证毕。
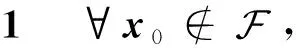
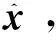
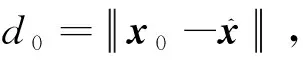

据引理1~2,得到网络的有限时间收敛定理:
定理2对任意初始点,网络(2)的状态向量x(t)都会在有限时间内收敛到可行域,并永驻其中。


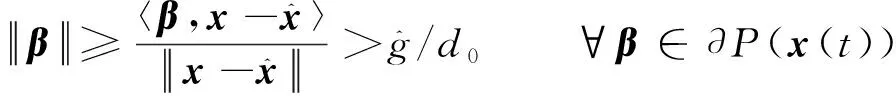
以及∃α∈∂f(x(t))使得
那么
(3)
对式(3)两边从0到t积分得到
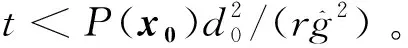
{t:P(x(t))>0,t∈[0,t1)}⊆

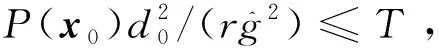

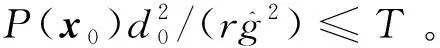


(4)
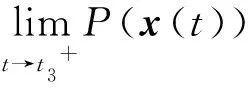
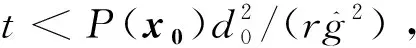
在证明网络(2)解的全局存在性前,需要如下的引理:

定理3对任意初始点,状态向量x(t)有界,网络(2)具有全局解。

因为x(t)绝对连续,易知E(x(t))是非负正则凸函数。根据命题3,存在可测函数α′(t)∈∂f(x(t)),β′(t)∈∂P(x(t)),使得
以及
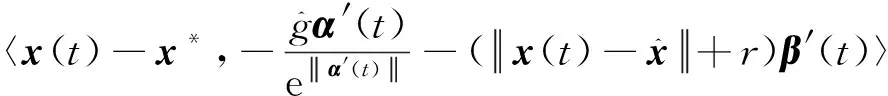
根据命题5又有
于是得到
从而,E(x(t))是单调不增的。立即有
那么
也即x(t)有界。再联合推论1,知∀x0=x(0)∈Rn,x(t)仍是有界的。根据解可扩展定理,网络(2)的解是全局存在的,即x(t)(∀t∈[0,+∞))。证毕。
设网络(2)的平衡点集为

定理4对任意初始点,网络(2)的状态向量x(t)都会收敛到其平衡点集E。


∀β(t)∈∂P(x(t))
再由命题3,存在可测函数α(t)∈∂f(x(t)),使得
接下来,得到
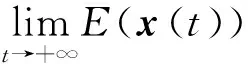
从而知

又因为∂f(x(t))及∂P(x(t))是非空紧凸上半连续的,故对0的任意一个闭邻域U,存在k0≥0,当k>k0时,有
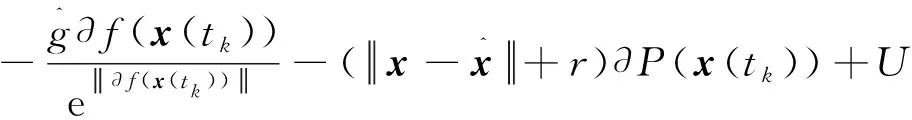
因为U任意,所以
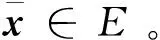
进一步地,可以得到如下关于网络(2)的更好的性质:

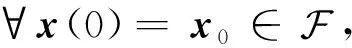
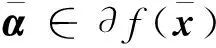
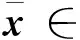
因为P(x(t))为凸函数,根据命题5,则有
〈x-x(tk),β(tk)〉≤P(x)-P(x(tk))≤0
那么
推出


4 仿真实例
本节将验证网络(2)的优化性能。实验在MatlabR2019a平台进行。误差精度(即程序运行过程中,相邻前后两次迭代得到的目标函数值之差的绝对值)取10-9。程序终止条件为误差精度小于10-9。
对于步长的选取,已有文献中普遍选用固定步长,但选用固定步长时,对于某些初始点,网络不能收敛到最优解,或者迭代次数会暴增,导致收敛时间大大增加。对此,是否可以取到这样的步长:它在网络的状态向量距离最优值点较远时,比较大;而当状态向量距离最优值点较近时,变得很小?
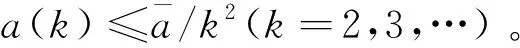

下面来分析这个原则在理论上的合理性。考虑如下不等式:
x(k+1)=x(k)+a(k)×D
其中

写成分量的形式就是:
xi(k+1)=xi(k)+a(k)×Dii=1,2,…,n其中,n为状态向量的维数。而
其中,i=1,2,…,n。且fi(x(k))与Pi(x(k))分别为∂f(x(k))与∂P(x(k))的第i个分量。
再来考察级数

另一方面,遵循变步长选取原则,经过仿真实例的大量编程尝试以及不断改善,本文最终总结出了两个较为适用的变步长选取公式:
1)a=a(k)=θ-b0-b1k-b2k2k≥2θ≥e常用的有θ=e,或θ=10。
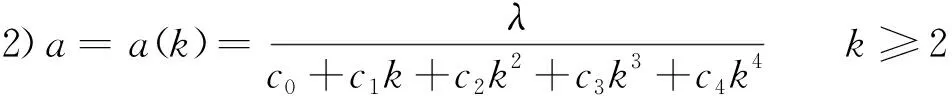
此外,一般而言:若选用固定步长,网络能够快速收敛到原优化问题的最优解;那么,改用变步长时,网络仍然能够以相近或更快的速度收敛到最优解;但反过来,却不一定成立。
我们将通过两个仿真实例来验证网络(2)的各项性能:其中,实例1用于与已有模型做性能比较;而实例2则主要突出变步长的作用——即它对网络收敛速度的促进作用。
实例1[18]考虑如下非光滑伪凸优化问题:
(5)
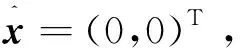
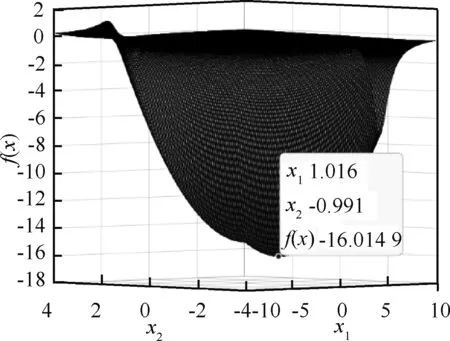
图1 实例1中f(x)的局部图像
其中
λ=2c0=100
c1=2×10-13c2=2×10-20
c3=2×10-19c4=5×10-23
最终状态向量收敛于式(5)的(近似)最优解:
x*=
(1.031 224 571 303 325,-1.000 004 386 209 420)T相应地,f(x*)≈-16.015 609 770 914 857。
图2表明网络(2)能够快速收敛到最优解,且耗时都少于7 s。
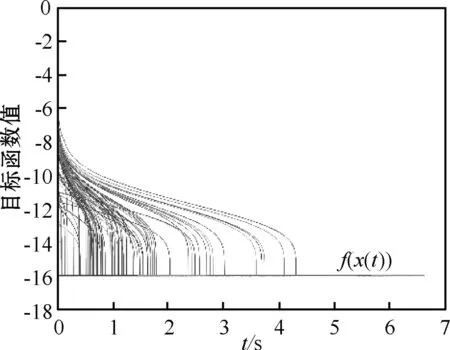
图2 实例1采用网络(2)求解时f(x)的变化趋势
需要指出的是文献[18]给出的最优解及函数最小值分别为(1,-1)T,-21。这与事实不符,因为点(1,-1)T对应的目标函数值为-16,但文献[18]中的图3和图4又明显地表明网络的状态向量及目标函数值分别收敛于点(1,-1)T及-21,不得不说文献[18]中图4的引用是一个令人遗憾的错误。
为突出网络(2)的先进性,仍然选取文献[18]中的模型重新进行实验,初始点、内点、步长及误差精度与前述一致,运行结果如图3所示。可以看出,网络也能快速收敛但目标函数值并不都收敛到优化问题的可行最小值,而且有的点耗时比网络(2)增加一倍以上,这说明与之相比较,网络(2)确实收敛得更快了。

图3 实例1采用文献[18]的模型求解时f(x)的变化趋势
另外,当步长固定为0.02时,网络(2)也能快速收敛,耗时不长但仍多于选用变步长的情形。效果如图4所示。

图4 实例1中步长为0.02时,f(x)的变化趋势
实例2[14]考虑如下非光滑伪凸优化问题:
(6)
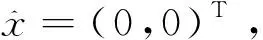
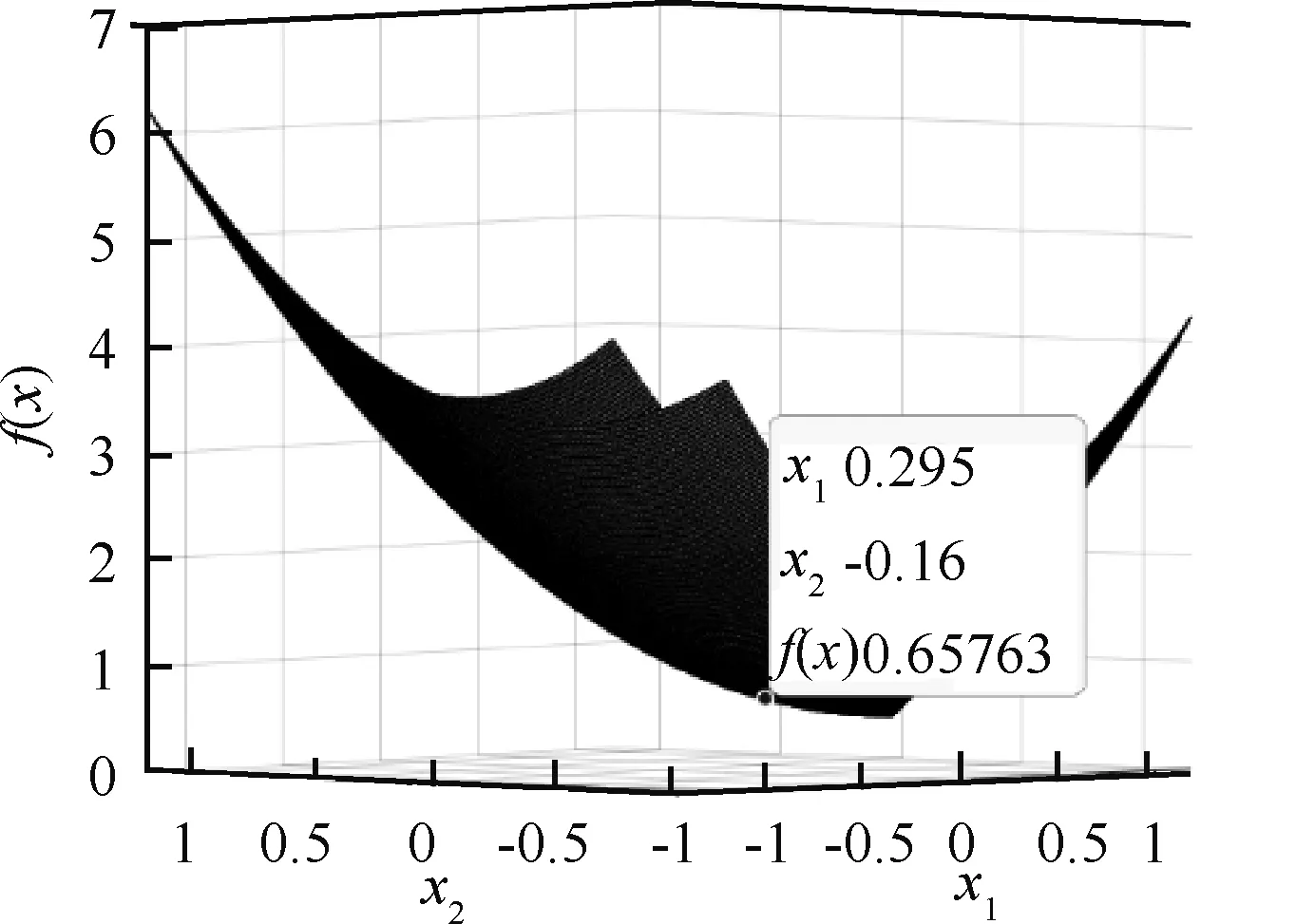
图5 实例2中f(x)的局部图像

表2 不同固定步长实验数据与结果
表2的数据表明,网络(2)从同一点(-1,1)T出发,以不同步长行进,迭代相同次数(5 000 000)后得到的目标函数值各不相同,且都没有达到目标函数在可行域内的最小值。结果如图6~10所示。从图中可以判断出:步长取0.000 1或0.000 01都较为合适。取0.01或0.001时,因为步长过大,造成振荡现象(步长取0.01时,振荡现象尤为明显);取0.000 001时,网络收敛速度最慢,说明步长并不是越小越好。同时,图6~10也表明,网络(2)的运行时间很长,都超过了35 s,这说明取固定步长时,网络(2)的收敛时间远大于35 s。
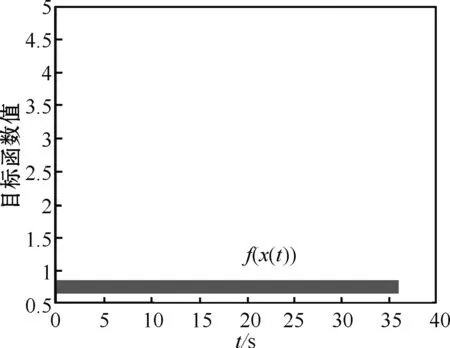
图6 实例2步长为0.01时,f(x)的变化趋势
作为对照,改用变步长做实验。初始点为区域[-2,2]×[-2,2]内任取的100个点。步长如下:
其中,
λ=1c0=1 083
c1=1×10-9c2=1×10-12
c3=1×10-13c4=1×10-15
最终状态向量收敛于式(6)的(近似)最优解:
x*=
(0.298 031 938 515 289,-0.161 176 963 583 877)T相应地,f(x*)≈0.655 592 147 866 133。
结果如图11~13所示,可以看到网络(2)快速收敛到式(6)的(近似)最优解,且耗时都小于5 s,这远小于取固定步长时网络(2)所需的收敛时间,证明了变步长对网络收敛的极大促进作用。图13则是对网络(2)的有限时间收敛定理的一个有力佐证。
值得注意的是,文献[14]给出的最优解及目标函数最小值分别为
(0.3,-0.165)T0.652
看起来比通过网络(2)获得的结果更优,实质上,点(0.3,-0.165)T不是可行解。导致出现该问题的原因:一方面很可能是数据处理不当,另一方面可能意味着文献[14]中的模型并不能保证状态向量进入可行域后不再离开。

图7 实例2步长为0.001时,f(x)的变化趋势
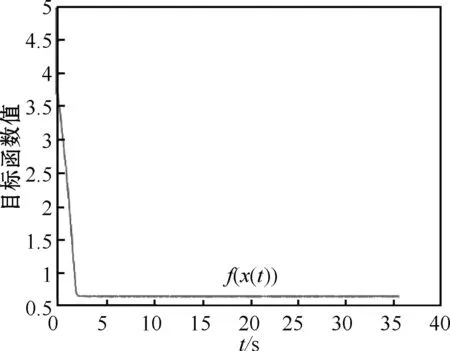
图8 实例2步长为0.000 1时,f(x)的变化趋势

图9 实例2步长为0.000 01时,f(x)的变化趋势

图10 实例2步长为0.000 001时,f(x)的变化趋势

图11 实例2中f(x)的变化趋势

图12 实例2中x1,x2的变化趋势
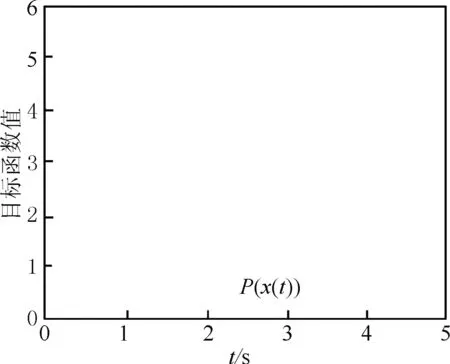
图13 实例2中P(x)的变化趋势
5 结束语
本文针对凸不等式约束的非光滑伪凸优化问题,提出了基于微分包含理论和罚函数思想的不带精确罚因子的神经网络模型。证明了网络存在全局解、可在有限时间内进入可行域且永驻其中,并最终收敛到原优化问题的最优解集。
为验证网络的性能,在MatlabR2019a平台用网络(2)对两个仿真实例进行求解。网络优化结果表明,对任意初始点,网络都能够快速收敛到原优化问题的最优解集。与已有模型相比,网络(2)能更快速地收敛到最优解,具有一定的优越性。
此外,有别于已有的文献大多采用固定步长进行网络求解,本文采用变步长进行网络求解,并给出了选择变步长时应当遵循的选取原则。同时在大量仿真实例的编程数据基础上总结出了两个较为适用的变步长选取公式。最后通过对比实验展示了变步长对加速网络收敛的极大促进作用。
下一步的研究方向可考虑非光滑混合约束伪凸优化问题的神经网络构造问题,以及进一步优化变步长选取过程。
——中国制药企业十佳品牌

