关于数据结构双向链表中插入节点的核心步骤探讨

雍巧玲

（喀什大学计算机科学与技术学院,新疆 喀什 844000）

1 引言

随着社会的发展和科技的进步，计算机已被广泛应用。由于计算机计算速度快，存储容量大，使用方便，用途广，给科技发展助力不少，不少高校设置了计算机相关专业及相关课程。其中，“数据结构”是计算机专业课程中的一门核心基础课程，课程内容包含了数据的各种存储结构和组织数据的方式。在数据结构中，双向链表是一种典型的数据存储结构，也是教学当中的重点案例。目前，在出版的一些数据结构相关教材中，对于双向链表中节点插入的讲解示例中，大多数只展示了指针方向变化的一种顺序[1-4]。在双向链表中，每一个节点都带有两个指针域和一个数据域[5]。在链表中，每插入一个节点，会有四个指针的指向发生变化，按照一定的操作顺序，就能完成节点的插入工作。

2 双向链表节点插入算法描述

2.1 基于双向链表节点的类型定义

在双向链表中，一个节点包括一个数据域、一个前驱和一个后继，分别用data、prior和next表示。基于双向链表的节点类型C语言模板如下[1]：

2.2 基于双向链表的节点前插入算法

在双向链表插入节点算法中，在第i个节点前（后）插入一个值为e的新节点s，第i个节点位置的定位可以在链表中从左向右方向查找到，也可以从右向左方向查找到。算法中，p为查找到的第i个节点，将待插入节点s插入到p节点之前，同时要修改s与p节点的前驱和后继域的位置。

在链表中插入一个节点需要对各指针域做出修改，在单向链表中插入一个节点只需要对p和s两个节点的后继域的指向分别做出更改，而在双向链表中，需要对p和s两个节点的前驱和后继共四个指针的指向分别做出更改。四个指针的变动，有四步操作语句，双向链表前插入节点的指针变换步骤的核心C语言代码如下[5]：

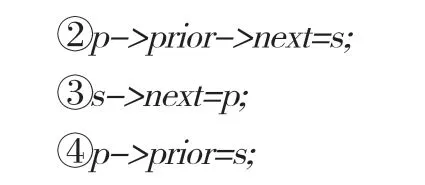
在上述代码语句中，①②③④分别代表四个指针的变化。指针改变的具体步骤解析如下。

步骤①：将插入节点s的前驱指向插入位置节点p的前驱，即将指定节点的前驱指针作为新节点的前驱指针。

步骤②：将p的前驱的后继域指向插入节点s，即调整新节点的前驱节点的后向指针。

步骤③：将插入节点s的后继域指向了p节点，即将指定节点p作为新节点的后向指针。

步骤④：将p节点的前驱域指向s节点，即将新节点作为指定节点的前向指针。

通过测试，上述代码的顺序不唯一，但也不是任意的。

2.3 基于双向链表的节点后插入算法

双向链表中，节点后插入算法与节点前插入算法的不同之处是，节点前插入算法是将新节点插入指定节点p与前一节点之间，而节点后插入算法是将新节点插入指定节点p与后一个节点之间，其代码执行语句也有所不同，但是同样需要对p和s两个节点的前驱和后继共四个指针的指向分别做出更改。四个指针的变动，有四步操作语句，双向链表后插入节点的指针变换步骤的核心C语言代码如下：

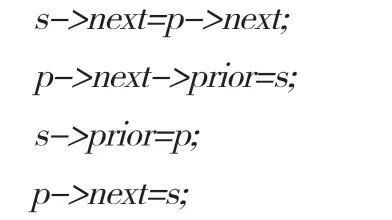
在上述代码语句中，①②③④分别代表四个指针的变化。指针改变的具体步骤解析如下：

步骤①：将插入节点s的后继指向插入位置节点p的后继，即将指定节点的后向指针作为新节点的后向指针；

步骤②：将p的next的prior域指向插入节点s，即调整p的next节点的前驱指针；

步骤③：将插入节点s的前驱域指向p节点，即将指定节点作为新节点的前向指针；

步骤④：将p的后继域指向s节点，即将新节点作为指定节点的后向指针。

通过测试，上述代码的顺序不唯一，但也不是任意的。

3 算法实验结果和分析

3.1 指针变化顺序排列

由2.2小节和2.3小节可知，编号①②③④分别代表双向链表中插入新节点的指针变化的四个操作步骤，双向链表插入节点的核心步骤的所有排列组合有24种，本节将对其分别做实验测试，其中，24种排列操作顺序如表1所示。

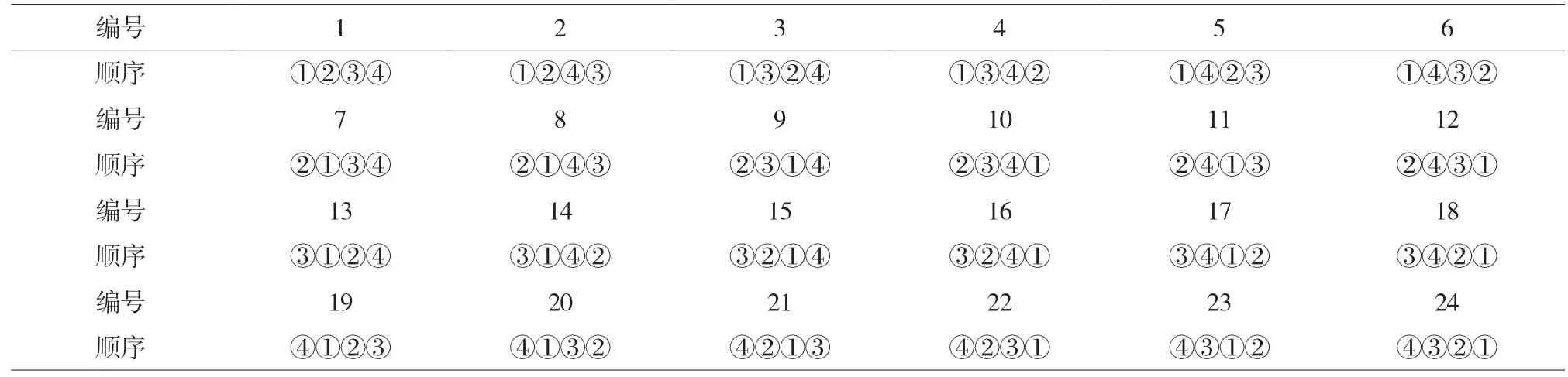
表1 双向链表插入节点步骤的24种排列顺序

无论是节点前插入算法还是节点后插入算法，其4个操作步骤的排列顺序都可由表1中的数据表示。本节需要注意的是，顺序1分别代表2.2小节和2.3小节中出现的节点插入的顺序，本文中也称此顺序为节点插入的标准顺序。

3.2 实验结果及分析

在本文中，实验对节点前、后插入算法的24种不同的顺序分别进行了测试，测试结果如下。

3.2.1 标准顺序下的节点插入操作

对于表1中的顺序1，无论是节点前插入算法还是节点后插入算法，均是教材中普遍出现的一种节点插入操作算法。在2.2小节和2.3小节中已给出其具体的C语言模板，其操作逻辑图如图1所示。

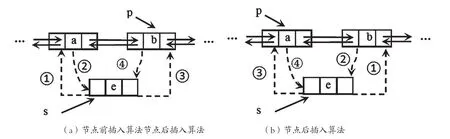
图1 顺序1节点插入操作图

由图1（a）可知，在元素a与b之间插入元素e，即在p节点之前插入s节点。在图1中，由①②③④四条虚线箭头和一个节点s完全替换a元素与b元素所属节点之间的双向实线箭头，从而顺利完成节点的前插入操作。由图1（b）可知，p指向了a元素所属节点，由于指定的p节点的位置不同，导致图1（a）与图1（b）中的虚线顺序有所不同，其目的都是改变指针指向完成节点的插入。

使用节点前插入算法构建一个双向链表，其中包含“a”“b”“c”三个字符元素。假设在第二个字符位置前插入元素“k”，插入元素之后，第二个位置的字符变更为“k”，原第二个位置及之后位置的字符依次往后顺延一位，即原字符顺序变为“akbc”。在实验中，输入“abc”三个字符构成双向链表，以“$”符为结束标识符，然后输入不同插入位置及插入元素“k”，插入节点后的链表结果如图2所示。

图2中的（a）—（c）分别代表第一、二和三个位置前插入元素“k”的实验结果，插入结果分别为“kabc”“akbc”“abkc”，由于本实验是节点前插入操作，所以无法实现在尾字符“c”之后插入元素节点。

使用节点后插入算法构建一个双向链表，其中包含“a”“b”“c”三个字符元素。假设在第二个字符位置后插入元素“k”，插入元素之后，原第三个位置的字符变更为“k”，原第三个位置及之后位置的字符依次往后顺延一位，即原字符顺序变为“abkc”。在实验中，输入“abc”三个字符构成双向链表，以“$”符为结束标识符，然后输入不同插入位置及插入元素“k”，插入节点后的链表结果如图3所示。

图2 节点前插入结果实现图

图3 节点后插入结果实现图

图3中的（a）—（c）分别代表第一、二和三个位置后插入元素“k”的实验结果，插入后的结果分别为“akbc”“abkc”“abck”，由于是节点后插入算法，所以无法实现在首字符“a”之前插入元素节点。

3.2.2 其他插入节点顺序

参照标准顺序1，在其基础之上改变指针指向的运算顺序，在表1中，节点前插入算法除了顺序1，还有顺序2、3、7、8、9、10、11、12、13、15和16，共计12种操作顺序可以完成节点的前插入操作，在节点后插入算法中除了顺序1，还有顺序2、3、4、5、6、7、8、9、13、14和15，但这些操作顺序在众多教材中出现的示例并不多。

通过实验测试，12种指针变化顺序都能很好地完成新节点的插入操作，与标准顺序1插入节点的效果一致。节点前插入算法插入节点结果实现图与图2完全一致，节点后插入算法插入节点结果实现图与图3完全一致。在本文中，经过代码的实现和测试，算法都能够很好地完成其在双向链表中的节点前插入操作和后插入操作。

从上述归纳的12种操作顺序中可以分析得出，在节点前插入算法中，语句④必须在语句②之后，在节点后插入算法中，语句④必须在语句①之后，否则无法完成双向链表中的节点插入操作。

3.2.3 非法操作顺序

对于节点前插入算法，若语句④在语句②之前，则程序先执行语句④“p->prior=s;”，后执行语句②“p->prior->next=s;”。例如操作顺序“①④②③”，先执行语句“①④”，同时替换掉链L1，即链L1断开。接着执行语句②，由于链L1已断开，无法找到“p->prior”节点，即无法找到图4（a）中a元素所属节点，将无法完成节点的插入操作。若想将a元素所属节点与s节点相连接，则执行语句“s->prior->next=s;”可以完成，但是这又违背了原代码语句的描述。

其他节点前插入算法中，不能插入节点的操作顺序的原理与以上所述一致。

对于节点后插入算法，若语句④在语句①之前，则程序先执行语句④“p->next=s;”，后执行语句①“s->next=p->next;”。例如操作顺序“②③④①”，语句④在语句①之前，完成了p的后继的指向，再执行语句①时，s的后继只能指向自己，无法指向原p节点的后继，即图4（b）中b元素所属的节点，从而无法完成节点的插入操作。

其他节点后插入算法中，不能插入节点的操作顺序的原理与以上所述一致。

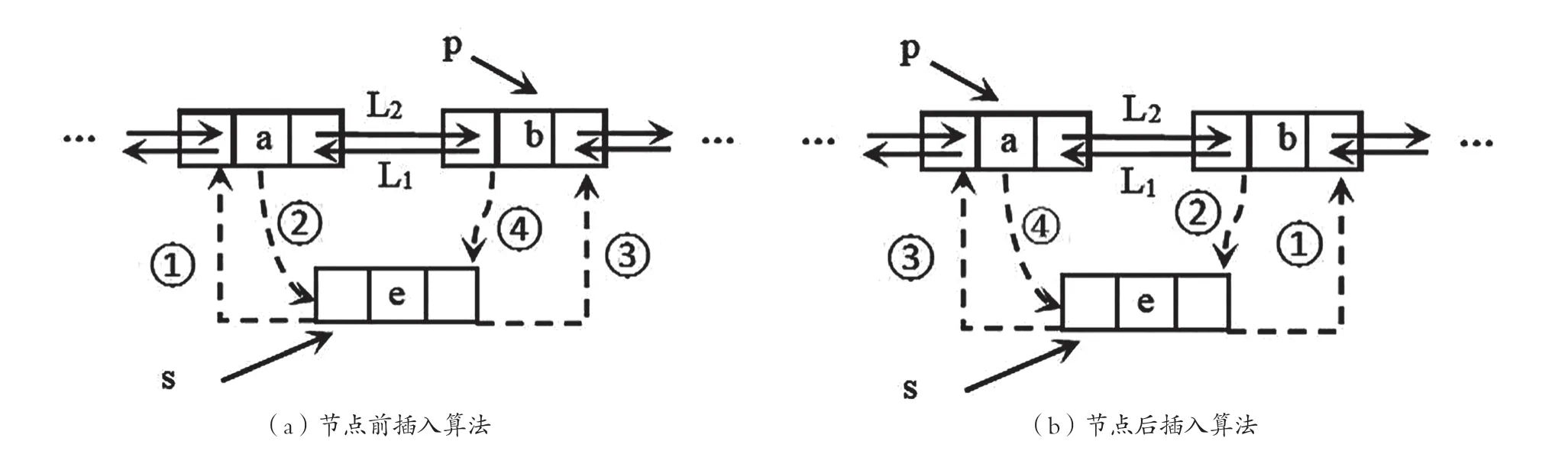
图4 双向链表节点插入指针替换图

4 总结

本文描述了双向链表中前、后插入节点的过程，其中，插入节点时四个指针的改变有不同的顺序。经过实验测试出，无论是节点前插入操作还是节点后插入操作，都有12种不同的操作顺序，同时也有12种不成立的顺序。从实验结果中分析出，节点前插入算法中，步骤②必须要在语句④之前，节点后插入算法中，步骤①必须要在语句④之前，否则指针指向会发生错误，会丢失存储的指针，从而导致算法无法完成节点插入。

在教学当中，可以让学生深入学习双向链表的节点类定义，以及链表的创建、节点的插入、删除等操作。在实验过程中，测试双向链表插入节点的基准运算顺序，同时也测试不同的运算顺序，让学生对这一知识点有更深入的了解和学习，可以抛出假设性问题，引起学生对这一知识点的好奇心和探究心理，激发学生的创新思维与学科交叉意识，从而提升学生的学习兴趣，并学以致用，让学生在不断探究的过程中收获知识，同时也可以加深其对知识点的记忆，从而达到由量变到质变的效果。